Похожие презентации:
Теоретическая механика. Кинематика. Курс лекций
1. Курс лекций по теоретической механике
Поволжский государственный технологический университетКафедра сопротивления материалов и прикладной механики
Лоскутов Ю.В.
Курс лекций по
теоретической
механике
Кинематика
Электронный учебный курс написан на основе лекций, читавшихся автором для студентов,
обучавшихся по специальностям СТР, ЭУН, ПЗ, АД, СУЗС и ТМО в ПГТУ (2001-2013 гг.).
Учебный материал соответствует календарным планам в объеме двух семестров.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра
Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional. Запуск
презентации – F5, навигация – Enter, навигационные клавиши, щелчок мыши, кнопки.
Завершение – Esc.
Замечания и предложения можно послать по e-mail: loskutovyv@volgatech.net
Йошкар-Ола - 2014
2. Содержание
Лекция 1. Кинематика точки. Способы задания движения. Уравнения движения. Траектория. Закондвижения точки. Связь между тремя способами задания движения. Скорость точки.
Лекция 2. Ускорение точки. Равнопеременное движение точки. Классификация движения точки.
Пример решения задач на определение кинематических характеристик движения точки. Кинематика
твердого тела. Виды движений. Поступательное движение.
Лекция 3. Вращательное движение. Угловая скорость и угловое ускорение. Равнопеременное
вращение. Скорость и ускорение точки тела при вращательном движении. Скорость и ускорение точки
вращающегося тела как векторные произведения. Формула Эйлера. Преобразование вращений.
Лекция 4. Плоскопараллельное движение твердого тела. Разложение плоского движения на
поступательное и вращательное движения. Уравнения движения. Теорема о сложении скоростей.
Следствия из теоремы. Мгновенный центр скоростей (МЦС).
Лекция 5. Примеры использования МЦС для определения скоростей. Теорема о сложении ускорений.
Мгновенный центр ускорений (МЦУ). Примеры использования теоремы о сложении ускорений и МЦУ
для определения ускорений
Лекция 6. Сферическое движение твердого тела. Теорема Эйлера. Угловая скорость и угловое
ускорение. Скорость и ускорение точки тела во сферическом движении. Общий случай движения.
Скорость точки свободного тела. Независимость векторов угловой скорости и углового ускорения от
выбора полюса. ускорение точки свободного тела.
Лекция 7. Сложное движение точки. Теорема о сложении ускорений точки при сложном движении.
Теорема о сложении ускорений при сложном движении точки. Ускорение Кориолиса. Причины
возникновения ускорения Кориолиса.
Лекция 8. Сложное движение твердого тела. Сложение поступательных движений. Сложение
вращательных движений. Сложение поступательного и вращательного движений. Общий случай
составного движения тела. Кинематические инварианты.
Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.1. М.: Высшая школа. 1977 г. 368 с.
2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.
3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.
4.
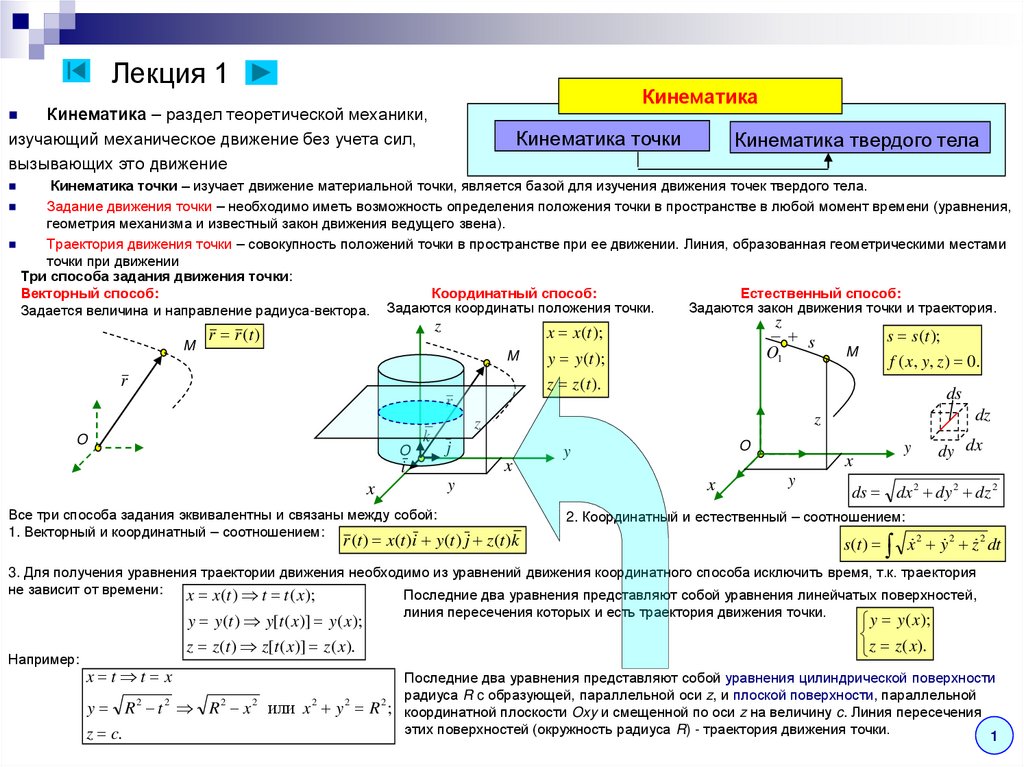
3. Лекция 1
КинематикаКинематика – раздел теоретической механики,
изучающий механическое движение без учета сил,
вызывающих это движение
Кинематика точки
Кинематика твердого тела
Кинематика точки – изучает движение материальной точки, является базой для изучения движения точек твердого тела.
Задание движения точки – необходимо иметь возможность определения положения точки в пространстве в любой момент времени (уравнения,
геометрия механизма и известный закон движения ведущего звена).
Траектория движения точки – совокупность положений точки в пространстве при ее движении. Линия, образованная геометрическими местами
точки при движении
Три способа задания движения точки:
Векторный способ:
Координатный способ:
Естественный способ:
Задаются закон движения точки и траектория.
Задается величина и направление радиуса-вектора. Задаются координаты положения точки.
M
z
r r (t )
z
s
O1
x x(t );
M
y y (t );
s s (t );
M
f ( x , y , z ) 0.
z z (t ).
r
ds
r
O
O
k
j
x
i
x
Все три способа задания эквивалентны и связаны между собой:
1. Векторный и координатный – соотношением:
dz
z
z
y
r (t ) x(t )i y(t ) j z (t )k
O
y
x
x
y
y
dy dx
ds dx 2 dy 2 dz 2
2. Координатный и естественный – соотношением:
s(t ) x 2 y 2 z 2 dt
3. Для получения уравнения траектории движения необходимо из уравнений движения координатного способа исключить время, т.к. траектория
не зависит от времени:
Последние два уравнения представляют собой уравнения линейчатых поверхностей,
x x(t ) t t ( x);
линия пересечения которых и есть траектория движения точки.
y y (t ) y[t ( x)] y ( x);
Например:
z z (t ) z[t ( x)] z ( x).
x t t x
y R2 t 2 R2 x2
z c.
y y ( x);
z z ( x).
Последние два уравнения представляют собой уравнения цилиндрической поверхности
радиуса R c образующей, параллельной оси z, и плоской поверхности, параллельной
или x 2 y 2 R 2 ; координатной плоскости Oxy и смещенной по оси z на величину c. Линия пересечения
этих поверхностей (окружность радиуса R) - траектория движения точки.
1
4. Лекция 1 (продолжение – 1.2)
Скорость точки – величина, характеризующая быстроту изменения положения точки в пространстве.Три способа задания движения точки определяют способы определения скорости точки:
Векторный способ: Сравним два положения точки в моменты времени t и t1= t + t:
v
Δr
r
t1 t Δt r1 r Δr ;
M1 v
ср
Δr
vср
Δt
- вектор средней скорости в интервале времени t,
направлен по направлению вектора перемещения (хорде MM1).
dr
dt
Δr
v
Δt
Предел отношения приращения функции
Δr
к приращению приращения аргумента есть Δt lim 0
Δt
производная функции (по определению):
- вектор мгновенной скорости точки (или просто скорости точки) в момент времени t, направлен
по касательной к траектории (при приближении M1 к M хорда занимает положение касательной).
Устремим t 0 и перейдем к пределу: Δt lim 0
v
r1
O
r;
t
M
dr
dt
r (t ) x(t )i y(t ) j z (t )k
Координатный способ: Связь радиуса-вектора с координатами определяется выражением:
v x 2 y 2 z 2 ;
z
vz
Используем векторную форму определения скорости:
M
x
dr (t ) d
cos(
v
,
x
)
;
vy v
x(t )i y (t ) j z (t )k Компоненты
Проекции
v
v
x
(
t
)
i
;
v
x
;
x
x
dt
dt
(составляющие)
скорости
vx
y
вектора
r
v
v
y
(
t
)
j
;
на оси
dx
dy
dz
y y; cos( v , y )
y
;
i
j
k
v
i
v
j
v
k
скорости:
x
y
z
координат:
z
v
O
k
dt
j
x
i
x
v z z .
v z z (t )k .
dt
y
cos( v , z )
y
z
.
v
Используем векторную форму определения скорости:
Естественный способ:
O
dt
Представим радиус-вектор как сложную функцию: r (t ) r [ s (t )].
v
dr (t ) dr ds dr
s .
dt
ds dt ds
dr
Δr
Представим производную
lim 0
.
s M
радиус-вектора как предел: ds Δs
Вектор приращения радиуса-вектора направлен по хорде MM1
Δs
O1
и в пределе занимает положение касательной.
Δs v
Величина
производной
Δr
При s 0 радиус кривизны 1 , угол
M1
2 sin Δ2
dr
Δr
радиуса-вектора
lim
lim
1
.
между радиусами кривизны 0, числитель Δs
Δ
0
0
r
по дуговой координате равна 1: ds
Δs
Δ
основание равнобедренного треугольника,
r1
знаменатель – длина круговой дуги радиуса .
Таким образом, производная радиуса-вектора по дуговой координате есть
единичный вектор, направленный по касательной к траектории.
Вектор скорости равен:
v s .
Проекция скорости на касательную:
При s 0 вектор скорости направлен в сторону увеличения дуговой
координаты, в противном случае – в обратную сторону.
v s .
Δr
Δ
1
Δs
2
5.
Лекция 2Ускорение точки – величина, характеризующая быстроту изменения скорости точки.
t
v;
Три способа задания движения точки определяют способы определения ускорения точки:
Векторный способ: Сравним скорости точки в двух положениях точки в моменты времени t и t1= t + t:
t1 t Δt v1 v Δv ;
M
Δv
v
v
- вектор среднего ускорения в интервале времени t, направлен в сторону вогнутости траектории.
a
Δr
r
r1
O
v1
a
ср
Δt
M1
v
v1
Переходя к пределу получаем:
Δt
a
dv d 2 r
dt dt 2
lim 0
Δv
a
Δt
Δt
lim 0
Δv dv
Δt
dt
- вектор истинного ускорения точки в момент времени t, лежит в
соприкасающейся плоскости (предельное положение плоскости, проведенной
через касательную в точке M и прямую, параллельную касательной в точке M1, при
стремлении M1 к M) и направлен в сторону вогнутости траектории.
Координатный способ: Используем полученное векторное выражение и связь радиуса-вектора с координатами
z
az
M
ay
r
O
k
ax
z
j
t
s O1M
т. М и s
t1 t Δt т. М1 и s s
O1
M
Проекции
ускорения
на оси
координат:
a x x i ;
a y y j;
a z z k .
a x 2 y 2 z 2 ;
a x x ;
x
a y y ; cos( a , x) ;
a
a z z .
y
cos( a , y ) .
a
Естественные координатные оси (касательная, главная нормаль, бинормаль)
y
x
Компоненты
(составляющие)
вектора
ускорения:
y
x
i
d 2 r (t ) d 2
a
2 x(t )i y (t ) j z (t )k
dt 2
dt
2
2
d x
d y
d 2z
2 i 2 j 2 k axi a y j az k
dt
dt
dt
r (t ) x(t )i y(t ) j z (t )k
M1 M
s
нормальная плоскость
Нормальная плоскость - это плоскость, перпендикулярная к
касательной M к траектории в точке.
нормальная плоскость
Соприкасающаяся плоскость представляет собой ту из
бесконечного множества
проходящих через
n плоскостей,
соприкасающаяся
плоскость
касательную M , которая
наиболее
тесно примыкает
к траектории в
O1 точки М. В случае
окрестности
плоской
траектории,
no
соприкасающаяся плоскость
совпадает с плоскостью траектории.
b
n
Спрямляющая
плоскость
- это плоскость, перпендикулярная
к
M o
нормальной bиoкасательной
плоскостям.
b
спрямляющая плоскость
3
6. Лекция 2 (продолжение 2.2)
Естественный способ: Используем векторное выражение для ускорения и выражение для скорости при естественной способе задания:s M
Δs
O1
avτ
n
Δ
r
M1
an
r
a
r1
O
a
dv d
d
( s ) s s
.
dt dt
dt
Представим единичный
касательный вектор
как сложную функцию:
При s 0 радиус кривизны 1 , угол
между радиусами кривизны 0, числитель основание равнобедренного треугольника,
образованного единичными векторами 1 и ,
знаменатель – длина круговой дуги радиуса .
Величина производной
единичного касательного вектора
по дуговой координате:
Производная единичного
касательного вектора:
(t ) [ s(t )].
1
Δ
1
d d ds
d
s .
dt
ds dt
ds
Угол между приращением единичного
вектора и самим вектором при 0,
стремится к 90о.
Или sin( / ) /
Δs
1
Δ
2 sin 2 1
d
Δ
Δs lim 0
Δ lim 0
.
ds
Δs
Δ
Введем единичный вектор n, нормальный (перпендикулярный) к касательной,
направленный к центру кривизны.
Компоненты
С использованием вектора n и ранее
(составляющие)
s 2
a s n . вектора
определенных величин
ускорение представляется как сумма векторов:
ускорения:
v s .
a s ;
Таким образом, производная
единичного касательного вектора
по дуговой координате есть вектор,
направленный перпендикулярно
касательной к траектории.
Проекции
ускорения
на оси и n:
s 2
an n .
aτ s ;
an
s 2
.
Таким образом полное ускорение точки есть векторная сумма двух ускорений:
касательного, направленного по касательной к траектории в сторону увеличения
дуговой координаты, если s 0 (в противном случае – в противоположную) и
нормального ускорения, направленного по нормали к касательной в сторону центра
кривизны (вогнутости траектории):
a a τ an .
Модуль полного ускорения:
a a τ an ;
2
2
4
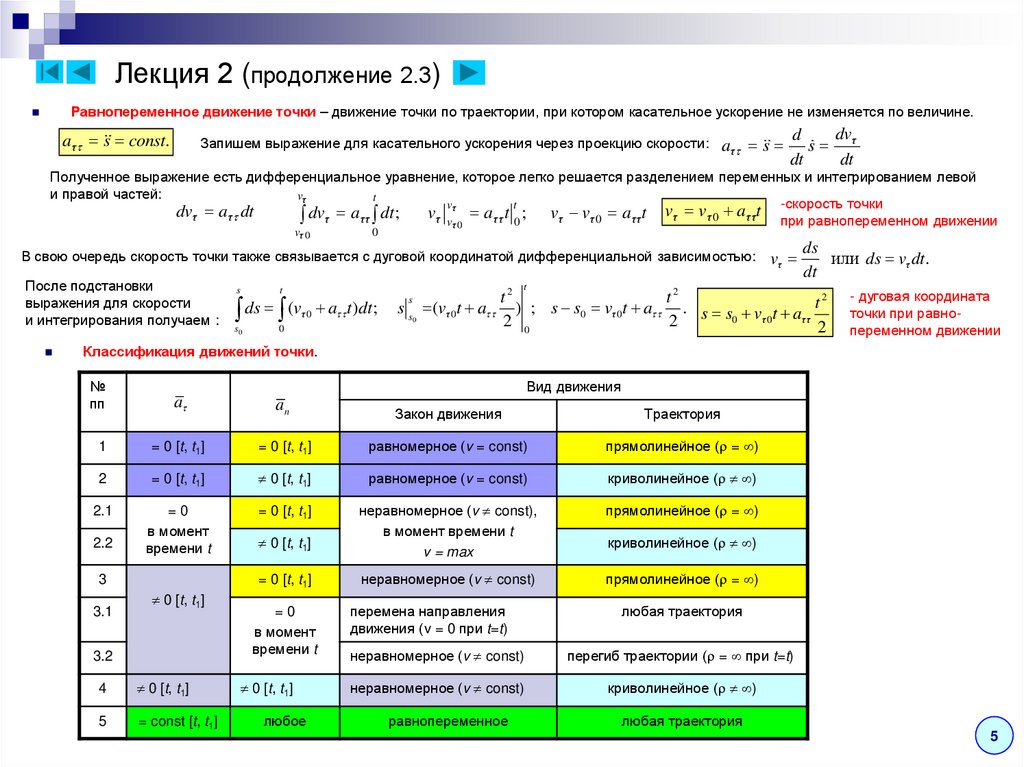
7. Лекция 2 (продолжение 2.3)
Равнопеременное движение точки – движение точки по траектории, при котором касательное ускорение не изменяется по величине.a τ s const.
Запишем выражение для касательного ускорения через проекцию скорости:
a τ s
dv
d
s τ
dt
dt
Полученное выражение есть дифференциальное уравнение, которое легко решается разделением переменных и интегрированием левой
и правой частей:
vτ
t
v
t
-скорость точки
dv τ a τ dt
dv
a
v τ vτ a τ τ t 0 ; v τ v τ 0 a τ τt vτ vτ 0 a τ τt при равнопеременном движении
τ
τ τ dt ;
τ0
vτ 0
0
В свою очередь скорость точки также связывается с дуговой координатой дифференциальной зависимостью: vτ
После подстановки
выражения для скорости
и интегрирования получаем :
s
ds (v
s0
t
t
τ0
a t )dt;
0
s
ss
0
ds
или ds vτ dt.
dt
2
t2
t2
(vτ 0t a ) ; s s0 vτ 0t a . s s v t a t
0
τ0
ττ
2 0
2
2
- дуговая координата
точки при равнопеременном движении
Классификация движений точки.
№
пп
Вид движения
a
an
Закон движения
Траектория
1
= 0 [t, t1]
= 0 [t, t1]
равномерное (v = const)
прямолинейное ( = )
2
= 0 [t, t1]
0 [t, t1]
равномерное (v = const)
криволинейное ( )
2.1
=0
в момент
времени t
= 0 [t, t1]
прямолинейное ( = )
0 [t, t1]
неравномерное (v const),
в момент времени t
v = max
= 0 [t, t1]
неравномерное (v const)
прямолинейное ( = )
2.2
3
3.1
0 [t, t1]
3.2
4
0 [t, t1]
5
= const [t, t1]
=0
в момент
времени t
0 [t, t1]
любое
перемена направления
движения (v = 0 при t=t)
криволинейное ( )
любая траектория
неравномерное (v const)
перегиб траектории ( = при t=t)
неравномерное (v const)
криволинейное ( )
равнопеременное
любая траектория
5





 Физика
Физика








