Похожие презентации:
Теоретическая механика Кинематика. Лекция № 6
1. Теоретическая механика Кинематика
Лекция № 62. 6.1 Основные понятия кинематики
Кинематикой называется раздел механики, в которомизучаются геометрические свойства движения тел без
учета действующих на них сил.
В теоретической механике рассматривается движение
тел относительного другого тела, с которым связана
система координат. Эта система координат называется
системой отсчета. Систему отсчета чаще связывают
с условно неподвижным телом. В технических
расчетах - с Землей.
Пространство в теоретической механике
рассматривают как трехмерное Евклидово.
Время в теоретической механике считают
универсальным, то есть одинаково текущим во всех
системах отсчета.
3.
Основная задача кинематики точки и твердоготела состоит в том, чтобы, зная их закон
движения, установить методы определения их
основных кинематических характеристик:
траектории, скорости, ускорения.
Задать закон движения точки или тела, значит
задать положение точки (тела) относительно
системы отсчета в любой момент времени.
Существует три способа задания движения точки
(тела): векторный, координатный,
естественный.
4. 6.2 ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Траектория движенияточки - геометрическое место
последовательных (с течением
времени) положений точки в
пространстве.
Закон движения точки М в
векторной форме задается
радиус-вектором
,
проведенным из точки
r Ок
точке М, как функции
времени t.
Z
r
k
O
i
X
r r (t ) r xi yj zk
j
M
z
y
x
Y
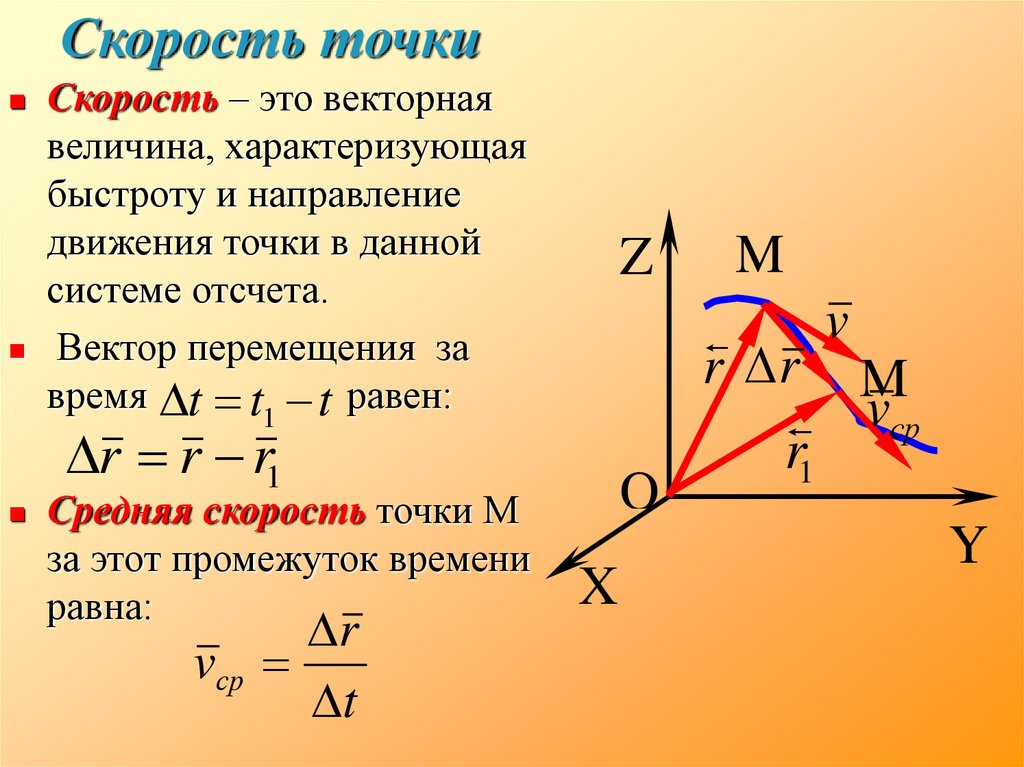
5. Скорость точки
Скорость – это векторнаявеличина, характеризующая
быстроту и направление
движения точки в данной
системе отсчета.
Вектор перемещения за
время t t1 t равен:
Z
r r r1
Средняя скорость точки М
за этот промежуток времени
равна:
r
vср
t
O
X
M
v
r r M
vср
r1 1
Y
6.
r drv lim (vср ) lim
r
t 0
t 0 t
dt
Вектор скорости v точки М
в данный момент времени
равен первой производной от
радиуса-вектора r по
времени t и направлен по
касательной к траектории
в сторону движения.
v 1м / c
Z
O
X
M
v
r r M
vср
r1 1
Y
7. Ускорение точки
За промежуток времени t t1 tточка переместится из
положения M в положение M1, и
при этом ее скорость изменится
от до . v
v1
v
aср
v v1 v
t
Вектор a ср как и вектор v
М
v
v
a ср
М1
a
v1
всегда направлен в сторону
вогнутости траектории.
a lim aср
t 0
v dv d r
lim
2 v r
t 0 t
dt
dt
2
v1
8.
Ускорение точки a характеризует изменениевектора скорости v по величине и направлению с
течением времени.
Ускорение a равно первой производной по
времени от вектора скорости v и второй
производной от радиус-вектора r точки М.
Вектор a лежит в соприкасающейся плоскости
и всегда направлен в сторону вогнутости
траектории.
Положение соприкасающейся плоскости
определяется предельным положением плоскости
проведенной через векторы v и v1при стремлении
2
точки М1 к точке М.
a 1м / с .
9. 6.3 Координатный способ задания движения точки
При координатном способе закон движенияточки в пространстве (уравнения движения
точки) задается тремя координатами
(декартовыми) как функциями времени:
X = f1(t); Y = f2(t); Z = f3(t);
на плоскости – двумя координатами:
X = f1(t); Y = f2(t);
при прямолинейном движении – одной
координатой:
X = f1(t).
Для получения уравнения траектории точки из
уравнений движения исключают время.
10. Скорость точки
ZСкорость точки dx
vX
vZ
v
k vX
r
i
X
j
vY
M
Y
x ;
dt
dy
vY
y ;
dt
dz
vZ
z
dt
Проекции вектора скорости
Так как r xi yj zk , то
на оси декартовых
скорость точки равна:
координат равны первым
dr dx
dy
dz
v
i
j k , производным от
dt dt
dt
dt
соответствующих
координат по времени.
но
v vX vY vZ
11. Скорость точки
Модуль вектора скорости равенv v v v
2
2
2
X
Y
Z
Вектор образует с осями координат углы,
определяемые направляющими косинусами
Z
vZ
v
cos v X ; v
X
;
v
vY
cos vY ; v ;
v
vZ
cos vZ ; v
v
v
k vX
r
i
X
j
vY
M
Y
12. Ускорение точки
УскорениеУскорение точки
равно:
2
2
2
точки
Z
aZ
dv d r d x
d y
d 2z
a
2 2 i 2 j 2 k
dt другой
dt
dt
dt
dt
С
стороны
a aX aY aZ
a
k
aX
r
aY
M
Y
dv X d 2 x
j
i
aX
2;
X
dt
dt Проекции вектора
ускорения на
2
dvY d y оси декартовых координат равны
aY
2 ; первым производным от проекций
dt
dt
скорости или вторым производным
2
dvZ d z от координат точки по времени.
aZ
2.
dt
dt
13.
Модуль вектора ускорения:a a a a
2
X
2
Y
2
Z
Углы вектора ускорения
с осями координат:
.
aX
cos a X ; a
;
a
aY
cos aY ; a ;
a
aZ
cos aZ ; a .
a
Z
aZ
a
k
i
X
aX
r
j
aY
M
Y
14. 6.4 Естественный способ задания движения точки
Для применения естественного способазадания движения точки должна быть известна
ее траектория.
Траектория точки может быть задана
различными способами:
уравнениями (возможно с неравенствами),
x2
y2
например,
1, 1 x 3;
4
9
словесно, например, радиус окружности равен 3м;
в виде графика в масштабе.
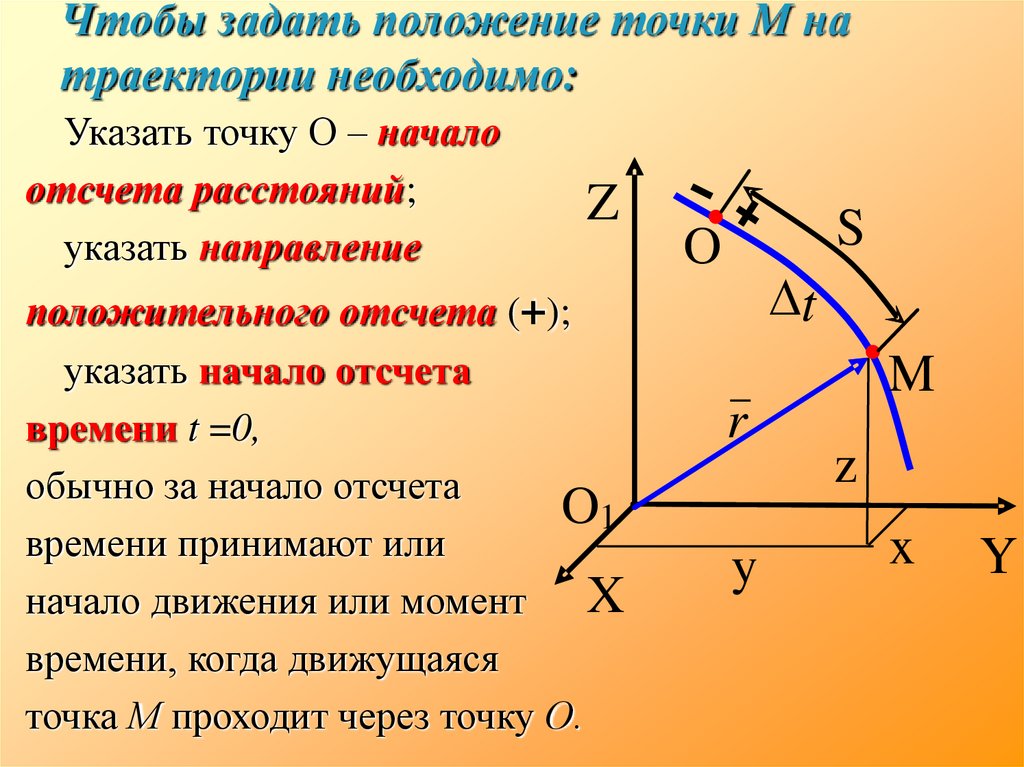
15. Чтобы задать положение точки М на траектории необходимо:
Указать точку О – началоотсчета расстояний;
указать направление
Z
положительного отсчета (+);
указать начало отсчета
времени t =0,
обычно за начало отсчета
O1
времени принимают или
X
начало движения или момент
времени, когда движущаяся
точка М проходит через точку О.
S
O
t
r
y
M
z
x
Y
16. Закон движения точки М по траектории:
s f t ,f t
Функция
определяет положение точки
на траектории, но не пройденный ею путь
Z
ds dx dy dz
2
2
S
O
2
t
r
O1
X
y
M
z
x
Y
17.
Если приZ
t 0, s 0
, то
S
O
t
.
t
s dx dy dz
2
2
r
2
O1
M
z
x
Y
0
X
Если известен закон движения точки в декартовых
координатах, то
dx x dt ;
dy y dt ;
dz z dt
y
t
s x y z dt
2
2
0
Это - связь естественного способа задания
движения точки с координатным.
2
18. Скорость точки
dr ds ds drv
dt ds dt ds
Z
S
O
t
r
O1
v
z
x
Y
dr
X
,
1
,
Но
единичный вектор направлен по
ds
касательной к траектории в сторону движения точки
М, следовательно, скорость точки М направлена по
касательной к траектории в сторону движения и
равна
y
M
ds
v
dt
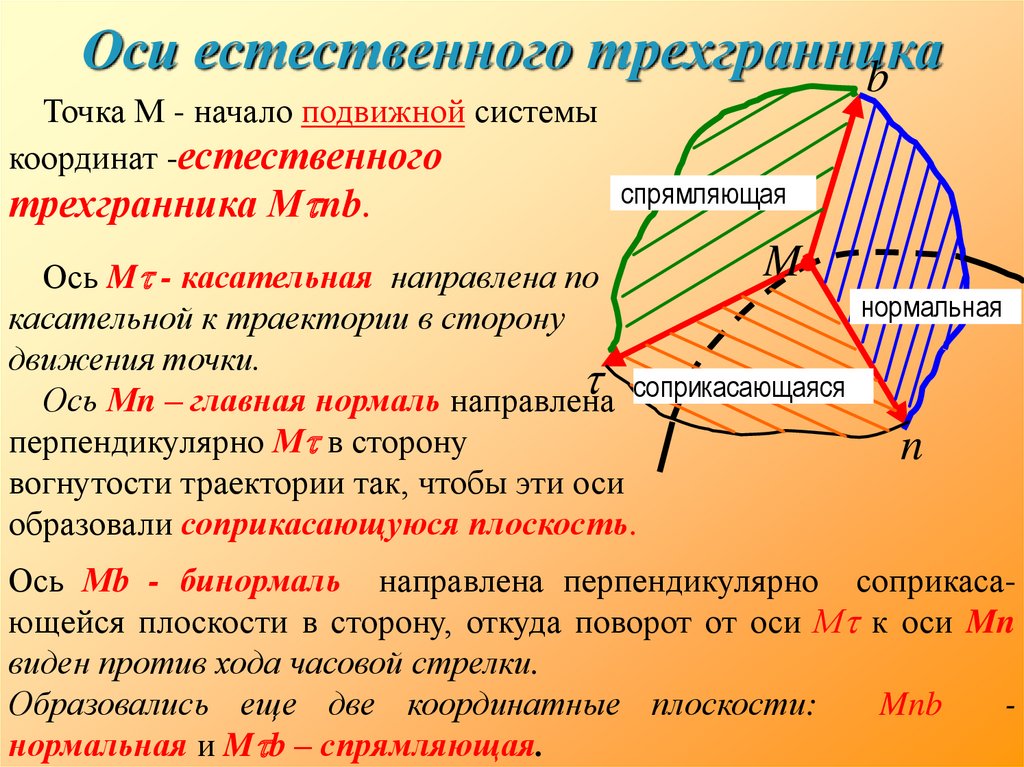
19. Оси естественного трехгранника
bТочка М - начало подвижной системы
координат -естественного
трехгранника М nb.
спрямляющая
M
Ось M - касательная направлена по
нормальная
касательной к траектории в сторону
движения точки.
Ось Мn – главная нормаль направлена соприкасающаяся
перпендикулярно М в сторону
n
вогнутости траектории так, чтобы эти оси
образовали соприкасающуюся плоскость.
Ось Мb - бинормаль направлена перпендикулярно соприкасающейся плоскости в сторону, откуда поворот от оси М к оси Mn
виден против хода часовой стрелки.
Образовались еще две координатные плоскости:
Mnb
нормальная и M b – спрямляющая.
20.
n1
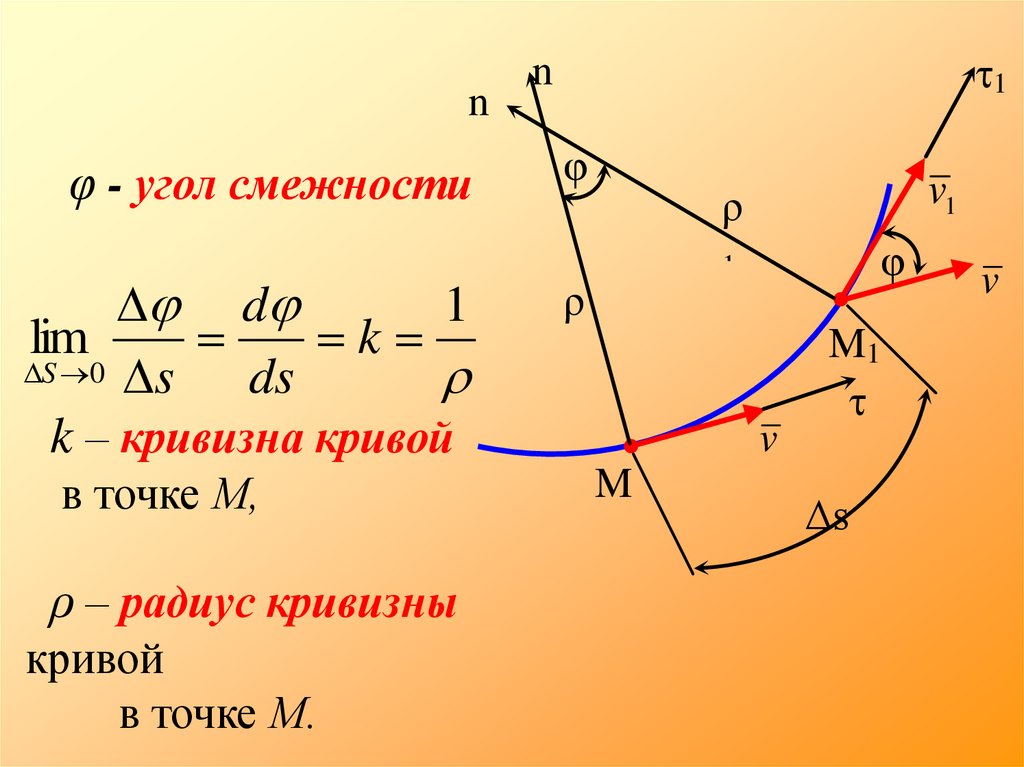
φ - угол смежности
d
1
lim
k
S 0 s
ds
k – кривизна кривой
в точке М,
ρ – радиус кривизны
кривой
в точке М.
1
n
φ
v1
ρ
φ
1
ρ
v
M
M1
Δs
v
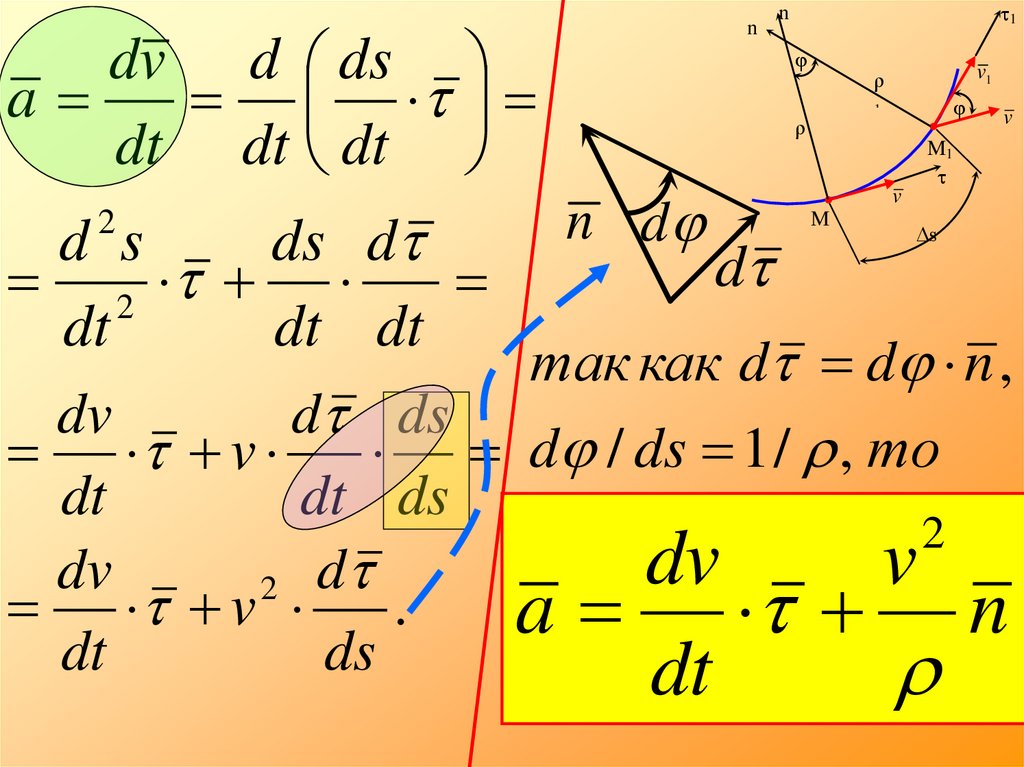
21.
n1
n
dv d ds
a
dt dt dt
2
n d
d s
ds d
d
2
dt
dt dt
так как d d n ,
dv
d ds
v
d / ds 1 / , то
dt
dt ds
2
dv
v
dv
2 d
v
.
a
n
dt
ds
dt
1
φ
v1
ρ
φ
1
ρ
v
M
M1
Δs
v
22. Ускорение точки М:
dvv2
a n
dt
Вектор a ускорения точки М разложен на две взаимно
перпендикулярные составляющие, лежащие в
соприкасающейся плоскости:
касательное
ускорение
dv
a
(тангенциальное), направленное по
dt касательной
к
траектории,
характеризующее
изменение
2
скорости
по величине;
v
нормальное
ускорение
a
n
n
направленное
перпендикулярно касатель- ному в
сторону
вогнутости
траектории,
характеризующее
изменение
скорости по направлению.
(центростремительное),
23. Ускорение точки равно:
a a an
n
Модуль ускорения равен:
a
a a
2
n 2
ρ
a
an
a v
M
Направление ускорения по отношению к нормали
определяется углом α:
n
a
cos
a
24. 6.5 Частные случаи движения точки
6.5 Частные случаи движения2
dv
v
точки
a n
6.5.1 Прямолинейное
движение
n
dt
dv
, a 0 a a
dt
Ускорение направлено по прямой так же как
и скорость , если точка движется ускоренно и в
противоположном направлении, если замедленно.
Ускорение меняется только по величине.
Если a const , то точка движется
равнопеременно: равнозамедленно или равноускоренно.
v
a
замедленное
v
a
ускоренное
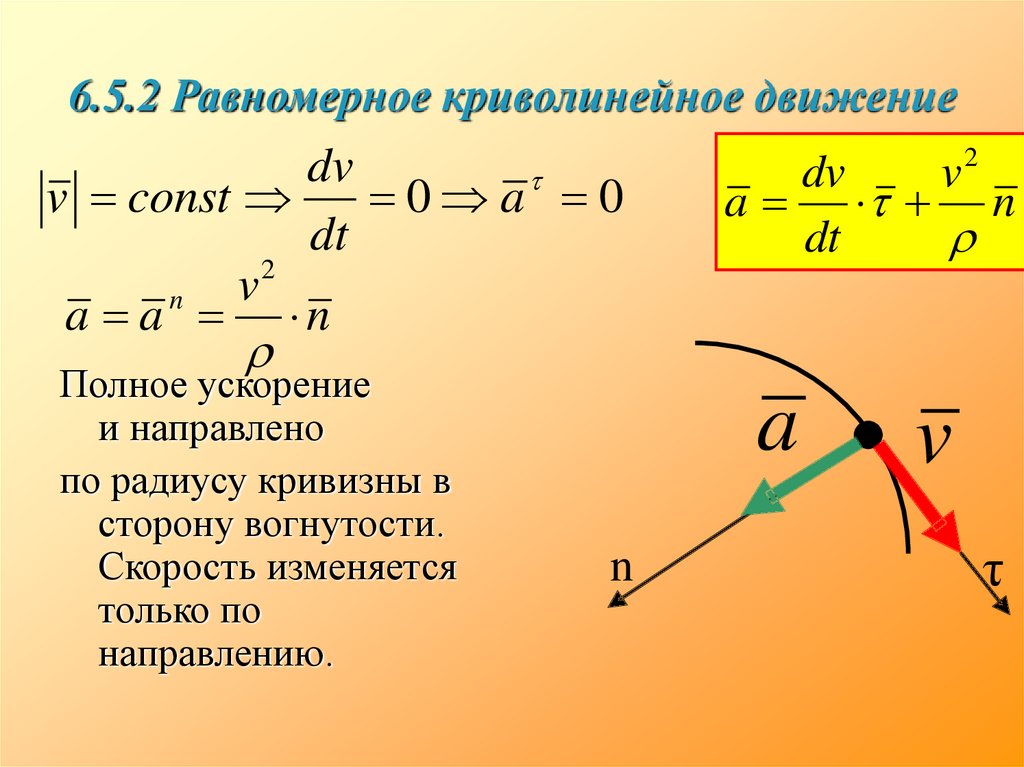
25. 6.5.2 Равномерное криволинейное движение
dvv const
0 a 0
dt
2
v
n
a a n
Полное ускорение
и направлено
по радиусу кривизны в
сторону вогнутости.
Скорость изменяется
только по
направлению.
2
dv
v
a n
dt
a
n
v
τ
26. 6.5.3 Равномерное прямолинейное движение
dvv const
0 a 0
dt
,
a 0
n
a a 0 a 0
n
dv
v2
a n
dt
Точка движется по прямой с постоянной скоростью
.
v const
s vt
v a 0
равномерное
прямолинейное
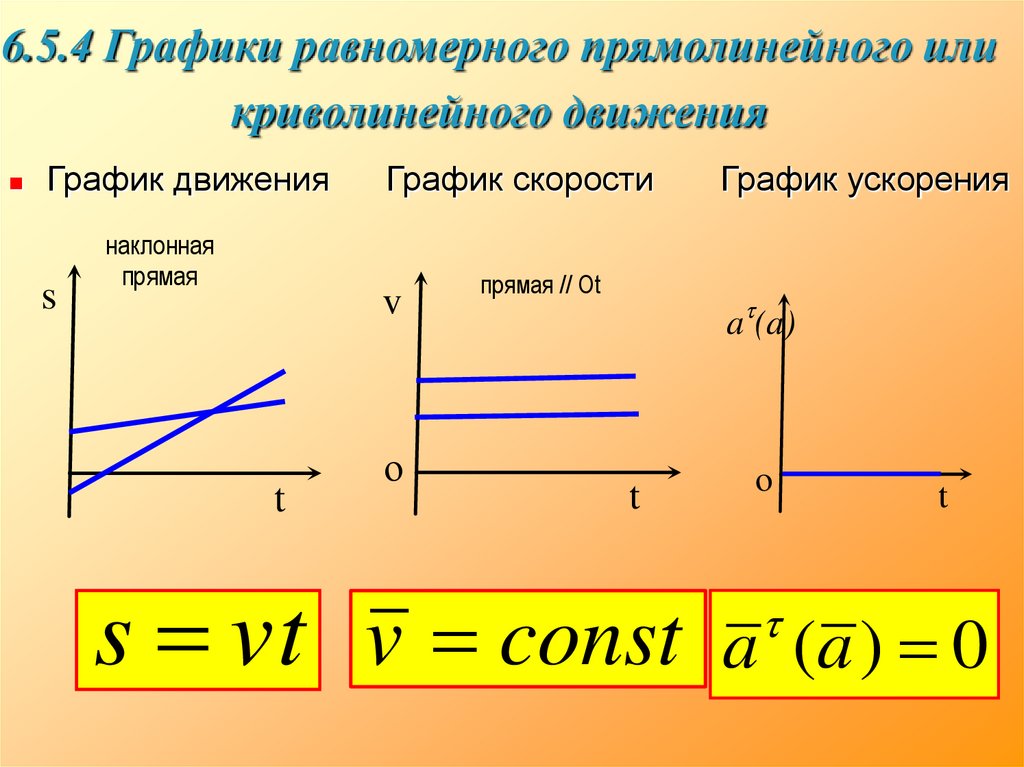
27. 6.5.4 Графики равномерного прямолинейного или криволинейного движения
График движенияs
наклонная
прямая
График скорости
v
t
о
прямая // Ot
График ускорения
a (a)
t
s vt v const
o
t
a (a ) 0
28. 6.5.5 Равнопеременное криволинейное движение
2dv
v
n
a const , a n
dt
dv a dt
интегрируем:
v a t C1
dv a dt
При t=0, v=v0 , C1=v0 ,
Скорость изменяется по закону:
v v0 a t
29.
dsv0 a t ds v0 dt a tdt
dt
ds
v
dt
a
tdt
0
t2
s v0t a
C2
2
при t =0, С2=s0 ,
Закон движения точки при ее равнопеременном
криволинейном движении имеет вид:
2
t
s s0 v0t a
2
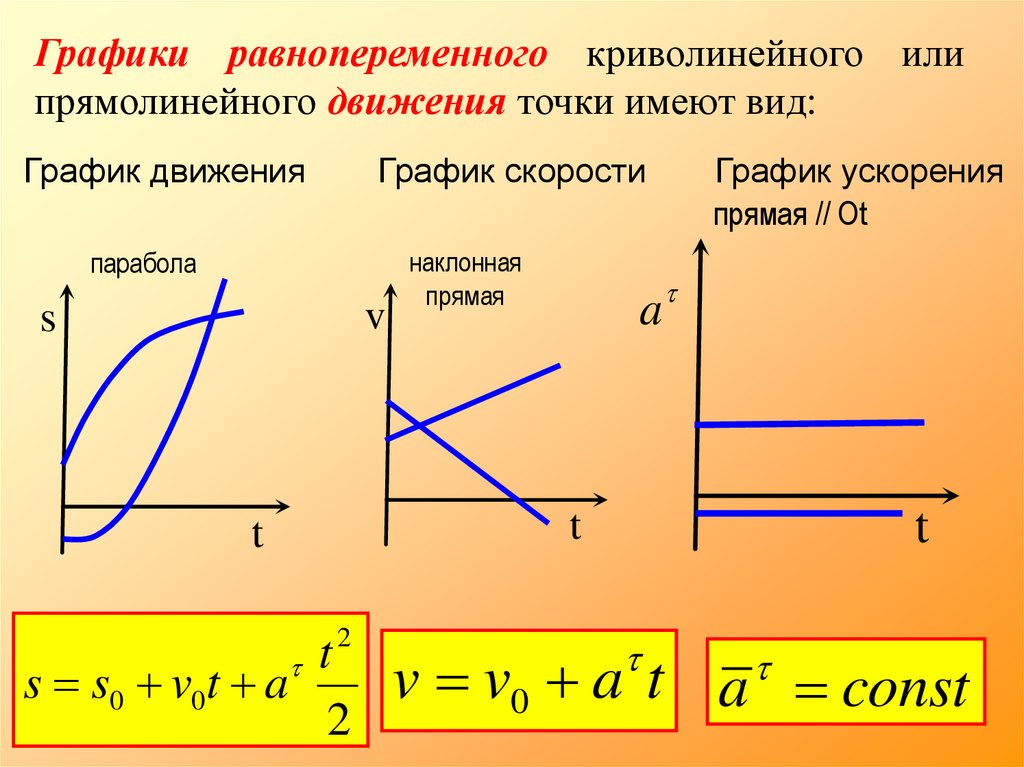
30.
Графики равнопеременного криволинейного илипрямолинейного движения точки имеют вид:
График движения
График скорости
парабола
v
s
наклонная
прямая
a
2
t
s s0 v0t a
2
t
t
t
График ускорения
прямая // Ot
v v0 a t a const






















 Физика
Физика








