Сформировать проблему исследования

1.

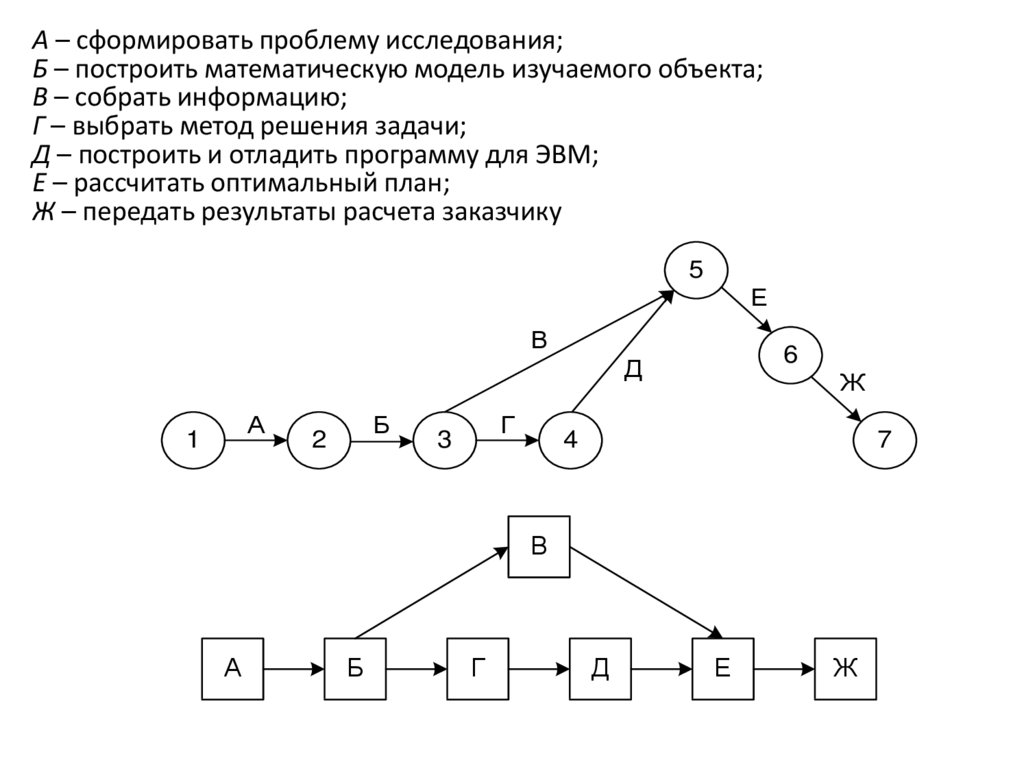
А – сформировать проблему исследования;
Б – построить математическую модель изучаемого объекта;
В – собрать информацию;
Г – выбрать метод решения задачи;
Д – построить и отладить программу для ЭВМ;
Е – рассчитать оптимальный план;
Ж – передать результаты расчета заказчику
5
Е
В
6
Д
А
1
Б
2
Г
3
Ж
4
7
В
А
Б
Г
Д
Е
Ж

2.

2
5
1
2
3
7
4
5
1
3
6
7
4
6
2
1
2
1
1
3
2
2
2'
1
А
С
4
1
3
2
Б
А
0
Д
5
Б
3
4
С
2
А
3'
5
4
3
2
1
С
Б
6
Д
5

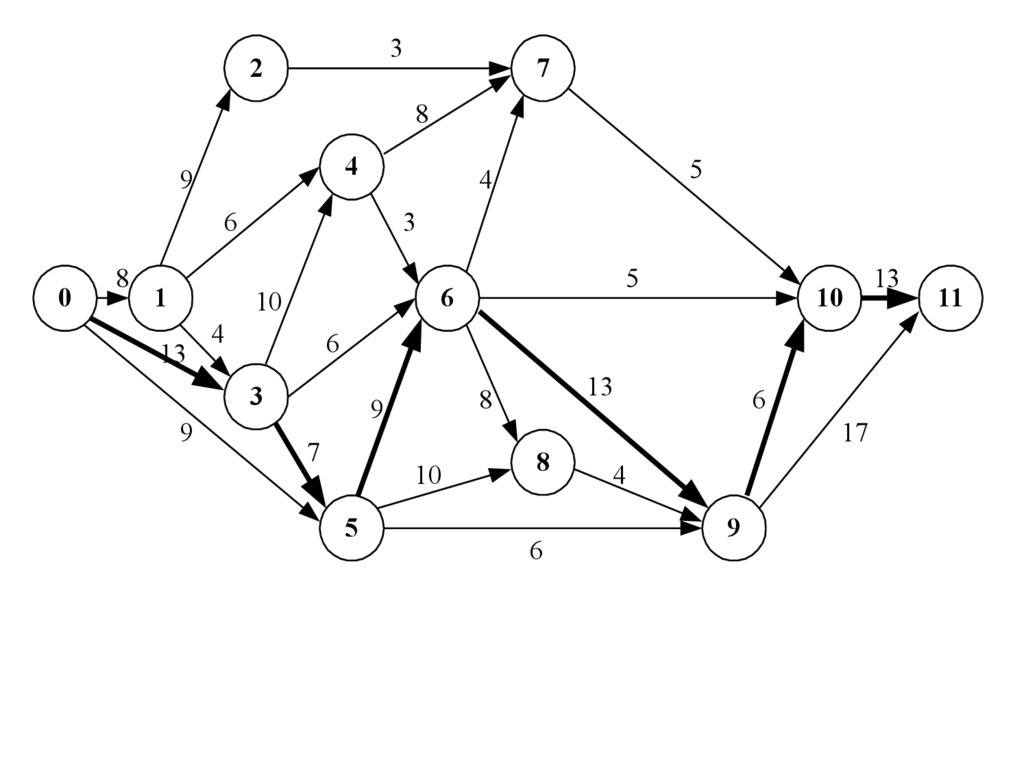
3.

1
4
8
0
2
5
9
7
3
6
10
11

4.

I
II
III
IV
V
4
VI
VII
VIII
IX
9
11
8
5
0
1
7
2
6
3
10

5.

3
2
7
8
4
9
3
6
0
8
1
4
10
6
3
9
5
6
10
13
5
4
9
7
10
5
13
8
8
6
6
17
4
9
13
11

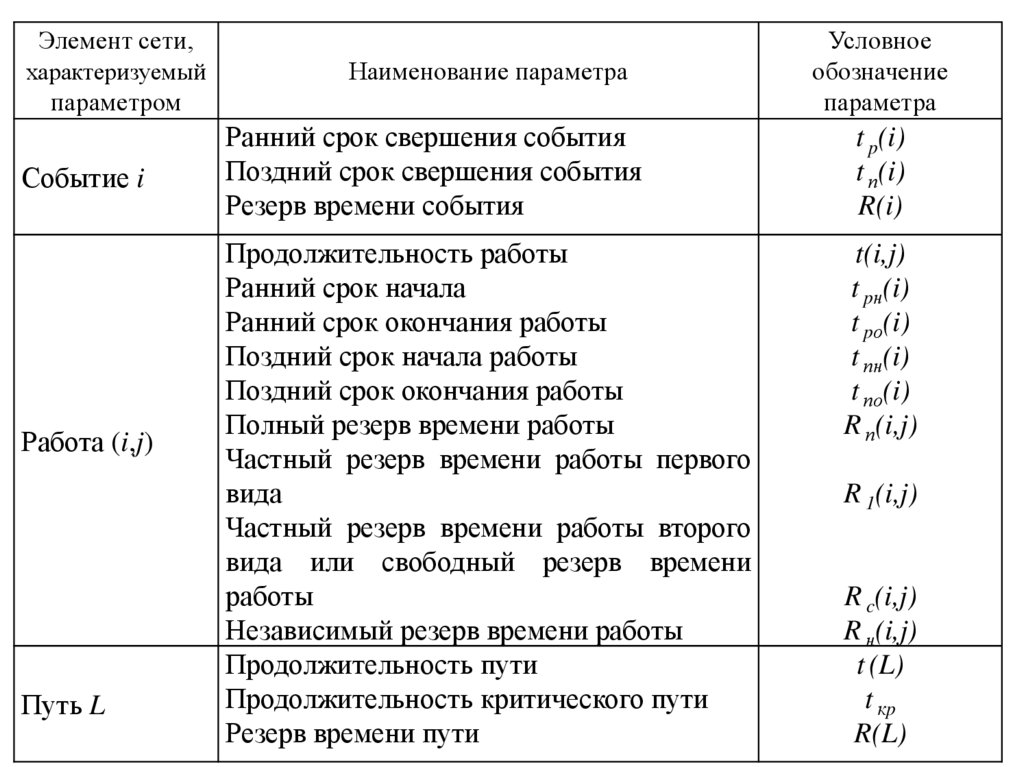
6.

Элемент сети,
характеризуемый
Наименование параметра
параметром
Событие i
Работа (i,j)
Путь L
Ранний срок свершения события
Поздний срок свершения события
Резерв времени события
Продолжительность работы
Ранний срок начала
Ранний срок окончания работы
Поздний срок начала работы
Поздний срок окончания работы
Полный резерв времени работы
Частный резерв времени работы первого
вида
Частный резерв времени работы второго
вида или свободный резерв времени
работы
Независимый резерв времени работы
Продолжительность пути
Продолжительность критического пути
Резерв времени пути
Условное
обозначение
параметра
t p(i)
t п(i)
R(i)
t(i,j)
t pн(i)
t pо(i)
t пн(i)
t по(i)
R п(i,j)
R 1(i,j)
R c(i,j)
R н(i,j)
t (L)
t кp
R(L)

7.

Ранний (или ожидаемый) срок tp(i) свершения i-го
события:
t (i )
t(L )
max
p
Lпi
ni
t p ( j ) max t p (i) t (i, j )
i, j
Поздний (или предельный) срок tп(i) свершения i-го
события:
tn (i ) tкр (i ) max t ( Lci )
Lci
tn (i) min tn ( j ) t (i, j )
i, j
Резерв времени R(i) i-го события:
R(i)= tп(i) – tр(i)

8.

2
7
3
17
33
8
5
4
9
23
4
3
6
0
0
8
1
6
8
10
4
13
6
8
3
8
13
13
37
9
10
48
5
29
6
9
7
10
5
20
4
6
9
42
17
13
11
61

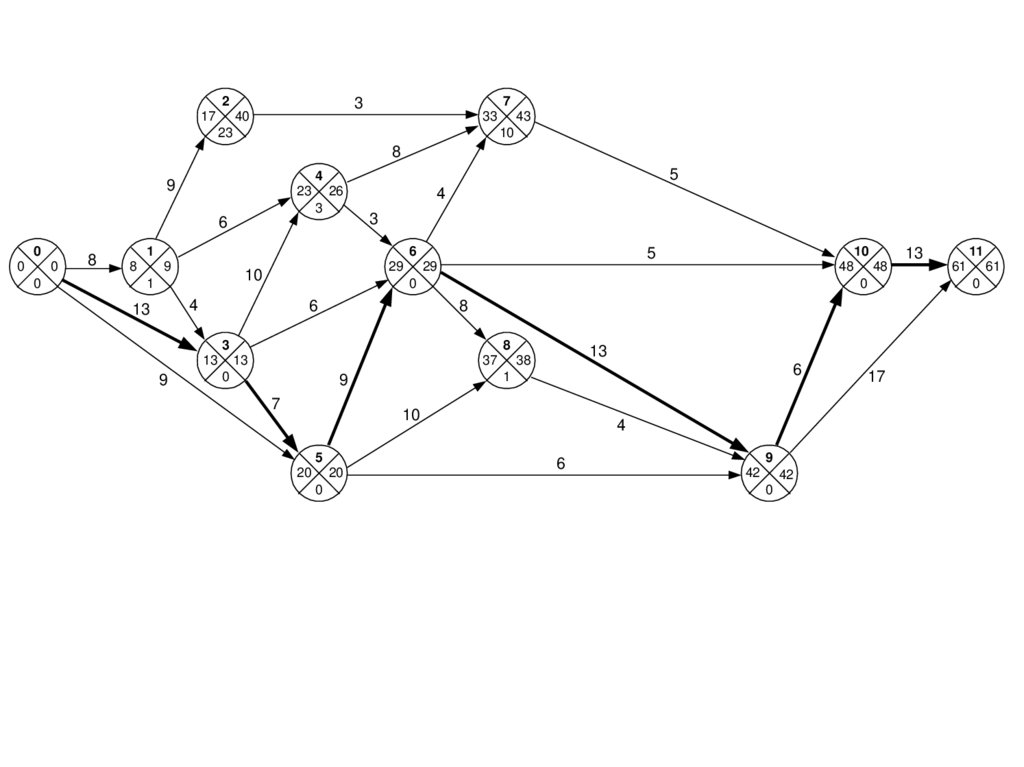
9.

2
7
3
40
17
43
33
10
23
8
5
4
9
26
23
3
3
6
0
0
0
0
8
4
6
1
9
8
10
1
8
3
9
0
6
1
9
7
13
38
37
13
10
5
20
20
0
4
6
9
42
42
0
13
11
61
61
0
0
8
6
13
48
48
0
4
13
10
5
29
29
17

10.

Параметры работ
Ранний срок tрн(i, j) начала работы (i, j):
tрн(i, j)= tр(i)
Ранний срок tро(i, j) окончания работы (i, j):
tро(i, j) = tр(i) + t(i, j)
Поздний срок tпо(i, j) окончания работы (i, j):
tпо(i, j) = tн(j)
Поздний срок tпн(i, j) начала работы (i, j):
tпн(i, j) = tн(j) - t(i, j)

11.

Полный резерв времени Rп(i, j) работы (i, j)
Rп(i, j) = tп(j) – tр(i) – t(i, j)
Частный резерв времени первого вида R1 работы (i, j)
R1(i, j) = tп(j) – tп(i) – t(i, j)
R1(i, j)= Rп(i, j) – R(i)
Частный резерв времени второго вида, или
свободный резерв времени Rс работы (i, j)
Rс(i, j) = tр(j) – tр(i) – t(i, j)
Rс(i, j) = Rп(i, j) – R(j)
Независимый резерв времени Rн работы (i , j)
Rн(i, j) = tр(j) – tп(i) – t(i, j)
Rн(i, j) = Rп(i, j) – R(i)

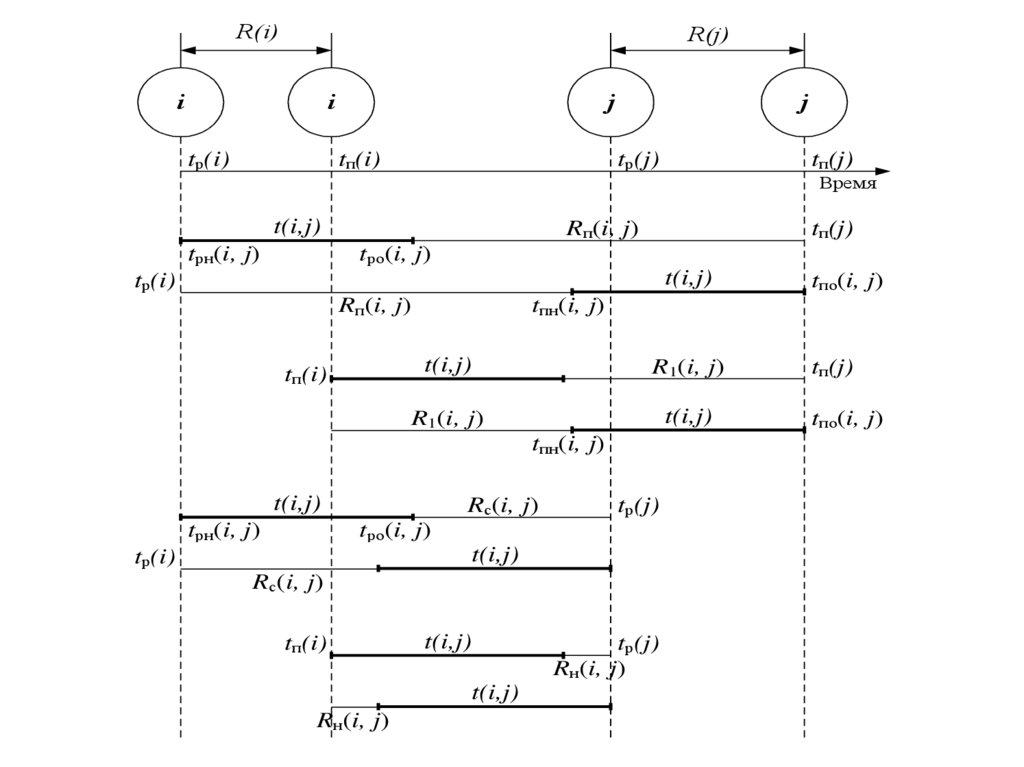
12.

R(i)
R(j)
i
i
tр(i)
j
tп(i)
j
tр(j)
tп(j)
Время
t(i,j)
tрн(i, j)
Rп(i, j)
tп(j)
tро(i, j)
t(i,j)
tр(i)
Rп(i, j)
tп(i)
tпн(i, j)
t(i,j)
R1(i, j)
R1(i, j)
t(i,j)
tпн(i, j)
t(i,j)
tрн(i, j)
Rс(i, j)
tр(j)
tро(i, j)
t(i,j)
tр(i)
Rс(i, j)
tп(i)
t(i,j)
t(i,j)
Rн(i, j)
tпо(i, j)
tр(j)
Rн(i, j)
tп(j)
tпо(i, j)

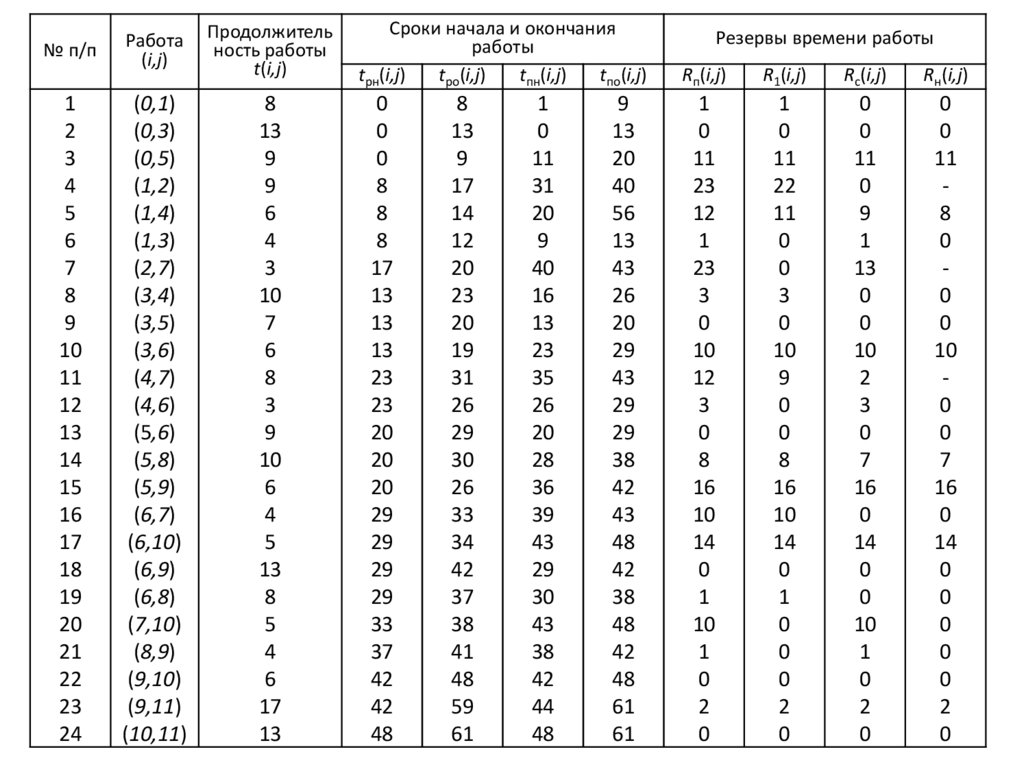
13.

№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Работа
(i,j)
Продолжитель
ность работы
t(i,j)
(0,1)
(0,3)
(0,5)
(1,2)
(1,4)
(1,3)
(2,7)
(3,4)
(3,5)
(3,6)
(4,7)
(4,6)
(5,6)
(5,8)
(5,9)
(6,7)
(6,10)
(6,9)
(6,8)
(7,10)
(8,9)
(9,10)
(9,11)
(10,11)
8
13
9
9
6
4
3
10
7
6
8
3
9
10
6
4
5
13
8
5
4
6
17
13
Сроки начала и окончания
работы
tрн(i,j)
tро(i,j)
tпн(i,j)
tпо(i,j)
0
0
0
8
8
8
17
13
13
13
23
23
20
20
20
29
29
29
29
33
37
42
42
48
8
13
9
17
14
12
20
23
20
19
31
26
29
30
26
33
34
42
37
38
41
48
59
61
1
0
11
31
20
9
40
16
13
23
35
26
20
28
36
39
43
29
30
43
38
42
44
48
9
13
20
40
56
13
43
26
20
29
43
29
29
38
42
43
48
42
38
48
42
48
61
61
Резервы времени работы
Rп(i,j)
R1(i,j)
Rc(i,j)
Rн(i,j)
1
0
11
23
12
1
23
3
0
10
12
3
0
8
16
10
14
0
1
10
1
0
2
0
1
0
11
22
11
0
0
3
0
10
9
0
0
8
16
10
14
0
1
0
0
0
2
0
0
0
11
0
9
1
13
0
0
10
2
3
0
7
16
0
14
0
0
10
1
0
2
0
0
0
11
8
0
0
0
10
0
0
7
16
0
14
0
0
0
0
0
2
0

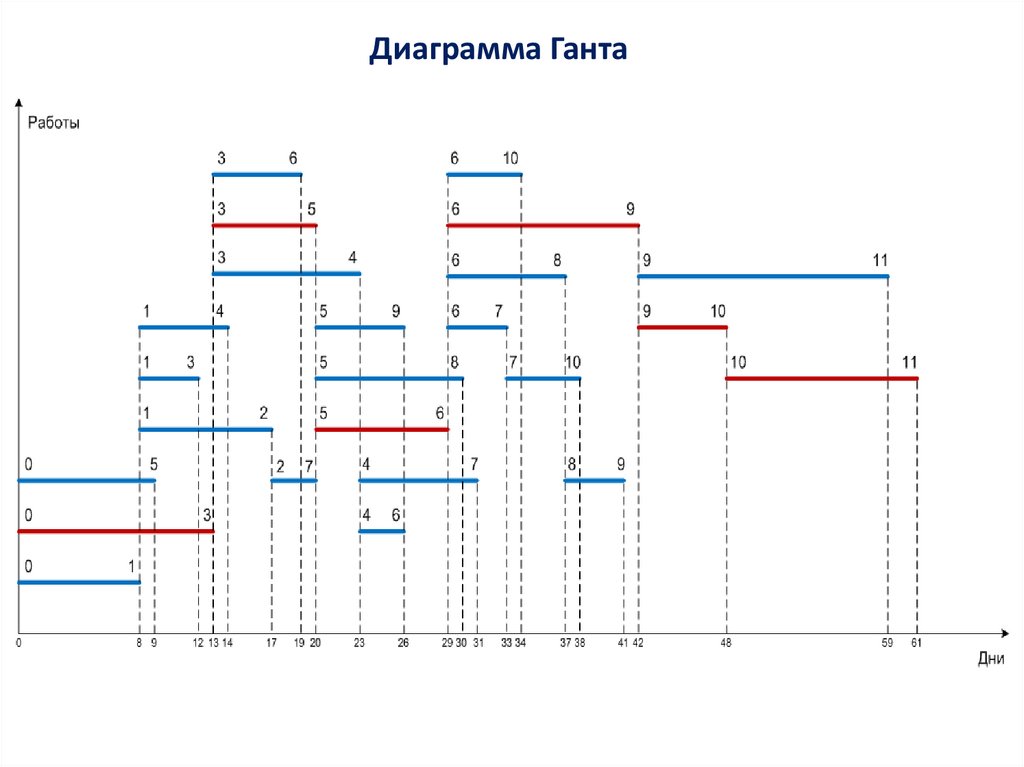
14.

Диаграмма Ганта

15.

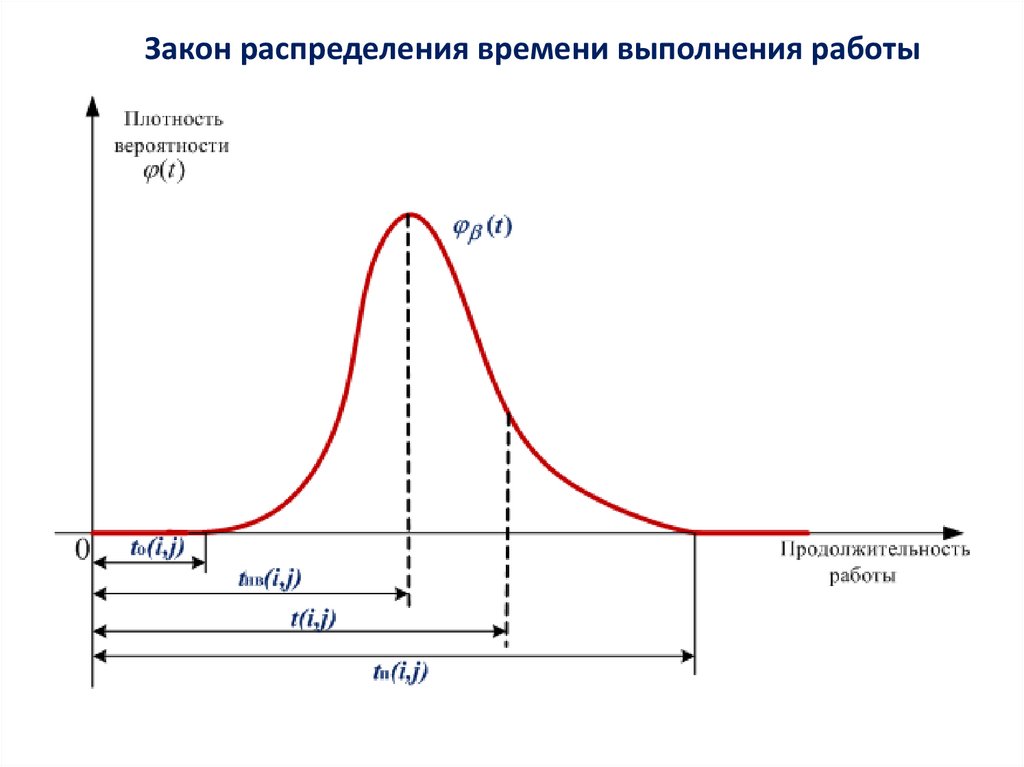
Закон распределения времени выполнения работы

16.

Среднее время выполнения работы:
t o (i, j ) 4t нв (i, j ) t n (i, j )
t (i, j )
6
2t o (i, j ) 3t n (i, j )
t (i, j )
5
Дисперсия времени выполнения работы:
t n (i, j ) t o (i, j )
(i, j )
6
2
2
Среднее время и дисперсия критического пути:
t ( i, j )
êð 2 ( Lêð ) 2 ( i , j )
t ( Lêð )
2
êð êð

17.

Вероятность выполнения проекта в заданный срок:
1 1 T t kp
P(tкр ≤ T) = Ф
2 2 kp
Ожидаемое время выполнения проекта:
Т t кр z кр кр

18.

Пример.
σ2(0,3)=2,5; σ2(3,5)=2,1; σ2(5,6)= 3,2; σ2(6,9)=4,0;
σ2(9,10)=1,5; σ2(10,11)=3,5
кp 2 (0,3) 2 (3,5) 2 (5,6) 2 (6,9) 2 (9,10) 2 (10,11)
2,5 2,1 3,2 4,0 1,5 3,5 16,8 4,1
Вероятность выполнения проекта за 63 дня:
1 1 63 61 1 1 2 1 1
Ф Ф(0,49)
P(tкр≤ T) = Ф
2 2 4,1 2 2 4,1 2 2
0,5 0,5 0,376 0,688 0,69
Ожидаемое время выполнения проекта:
β=0,95
T = 61+ z0,95*4,1 = 61 + 1,96*4,1 ≈ 69

19.

Коэффициент напряженности работы:
К н (i, j )
t ( Lmax ) t кр
t кр t кр
Rn (i, j )
К н (i, j ) 1
t кр t кр
Зоны:
критическая - Kн(i, j) > 0,8
подкритическая - 0,6 ≤ Kн(i, j) ≤ 0,8
резервная - Kн(i, j) < 0,6
Пример.
Путь максимальной продолжительности, проходящий через (1, 4):
L4: 0→1→4→ 6→9→10→11
= 13 + 6 + 13 = 32 (суток)
t кр
t (Lmax) = t (L4) = 49 (суток)
Коэффициент напряженности работы (1, 4):
49 32 17
12
17
К н (1,4)
0,59
К н (1,4) 1
0,59
61 32 29
61 32 29