Похожие презентации:
Параллельность в пространстве. Признак перпендикулярности прямой и плоскости
1.
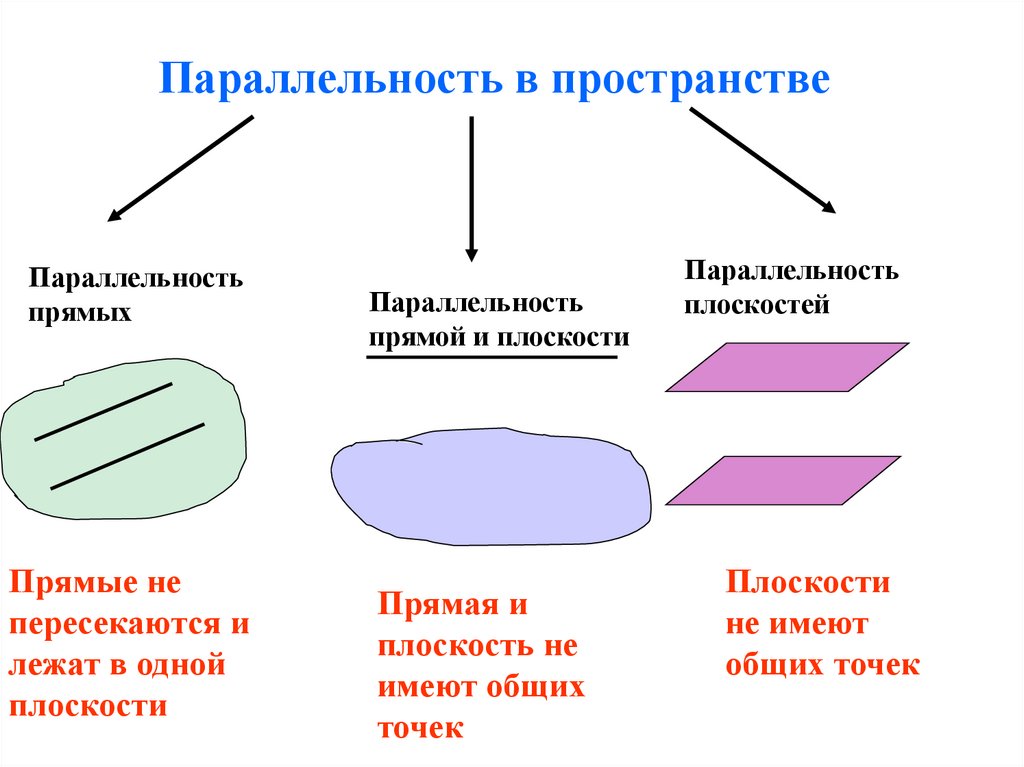
Параллельность в пространствеПараллельность
прямых
Прямые не
пересекаются и
лежат в одной
плоскости
Параллельность
прямой и плоскости
Прямая и
плоскость не
имеют общих
точек
Параллельность
плоскостей
Плоскости
не имеют
общих точек
2.
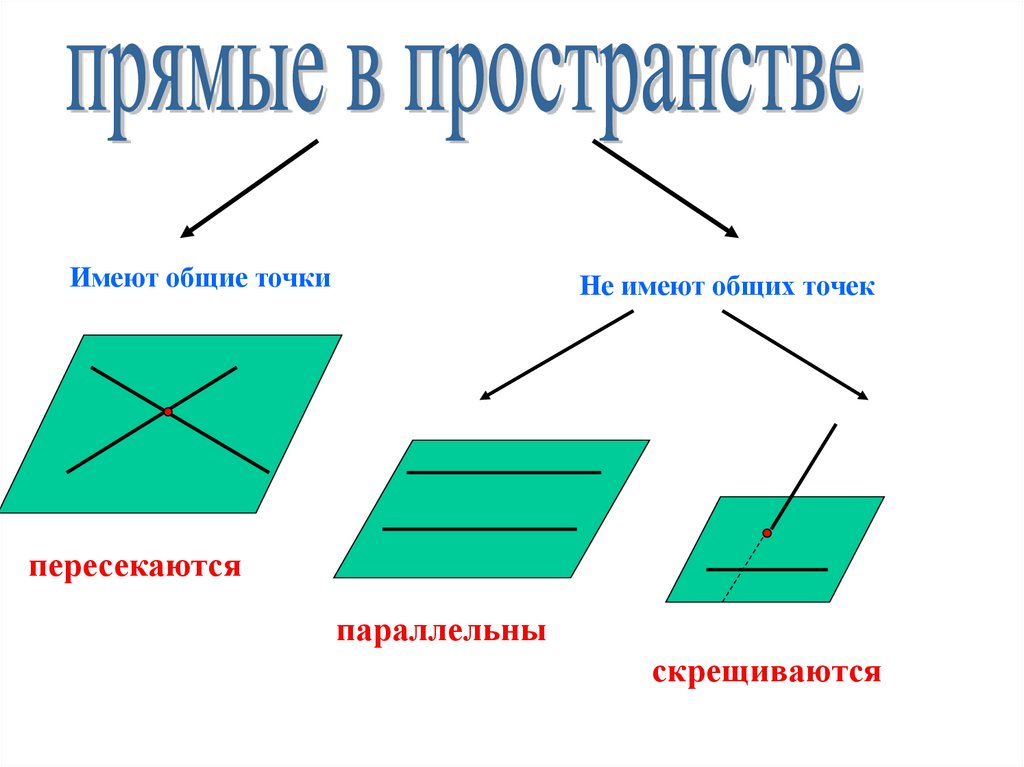
Имеют общие точкиНе имеют общих точек
пересекаются
параллельны
скрещиваются
3.
Если две прямые параллельны третьейпрямой, то они тоже параллельны
Дано: а||b; c||b
a
Доказать : a||c
b
c
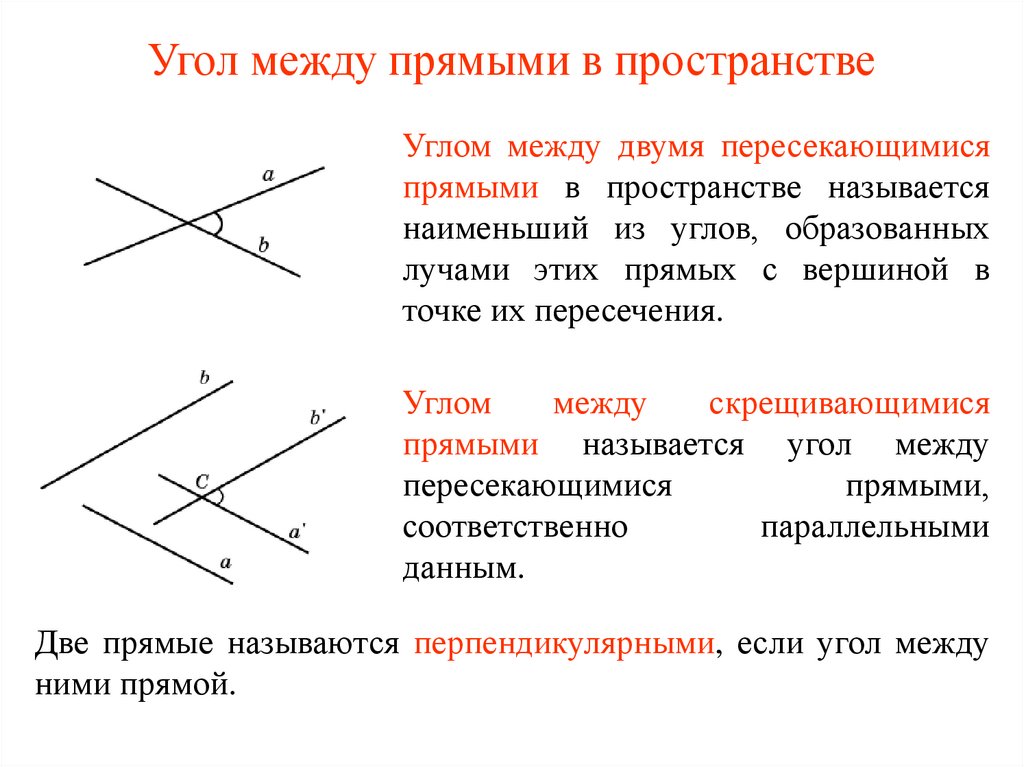
4. Угол между прямыми в пространстве
Углом между двумя пересекающимисяпрямыми в пространстве называется
наименьший из углов, образованных
лучами этих прямых с вершиной в
точке их пересечения.
Углом
между
скрещивающимися
прямыми называется угол между
пересекающимися
прямыми,
соответственно
параллельными
данным.
Две прямые называются перпендикулярными, если угол между
ними прямой.
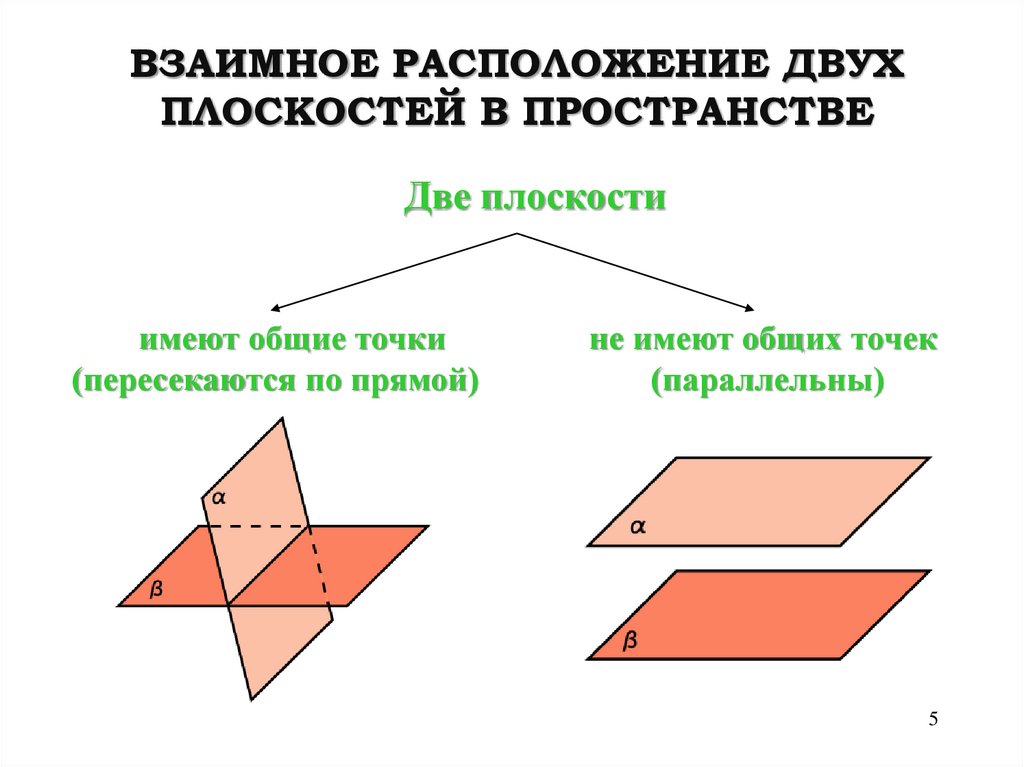
5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
Две плоскостиимеют общие точки
(пересекаются по прямой)
не имеют общих точек
(параллельны)
5
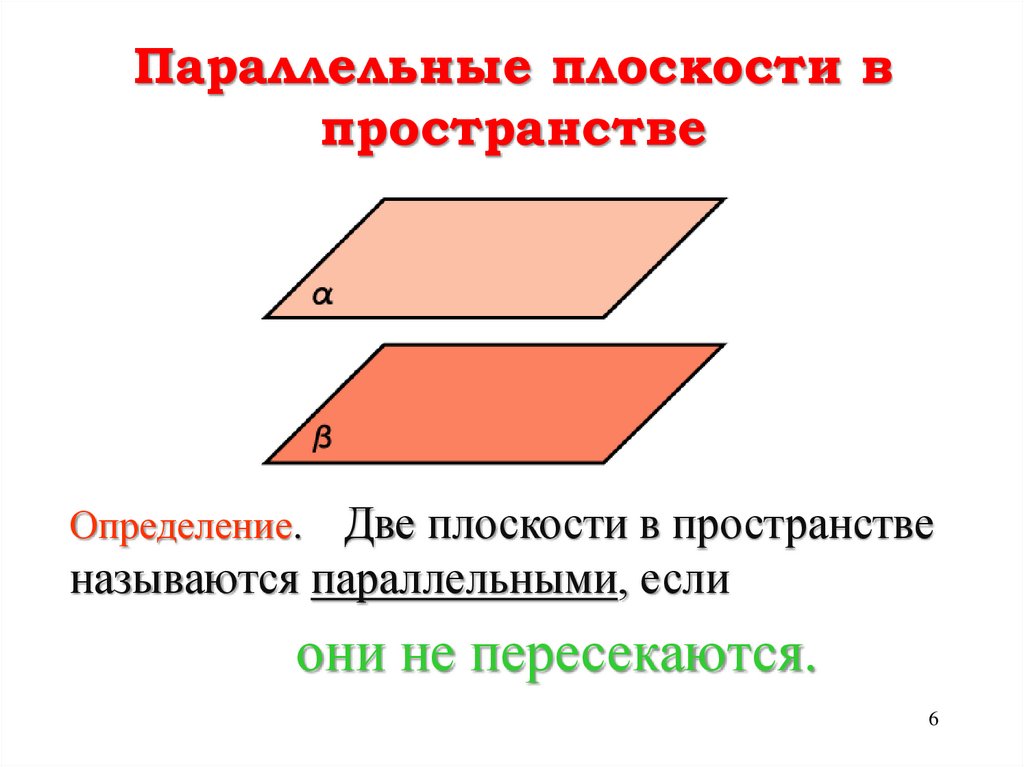
6. Параллельные плоскости в пространстве
Две плоскости в пространственазываются параллельными, если
Определение.
они не пересекаются.
6
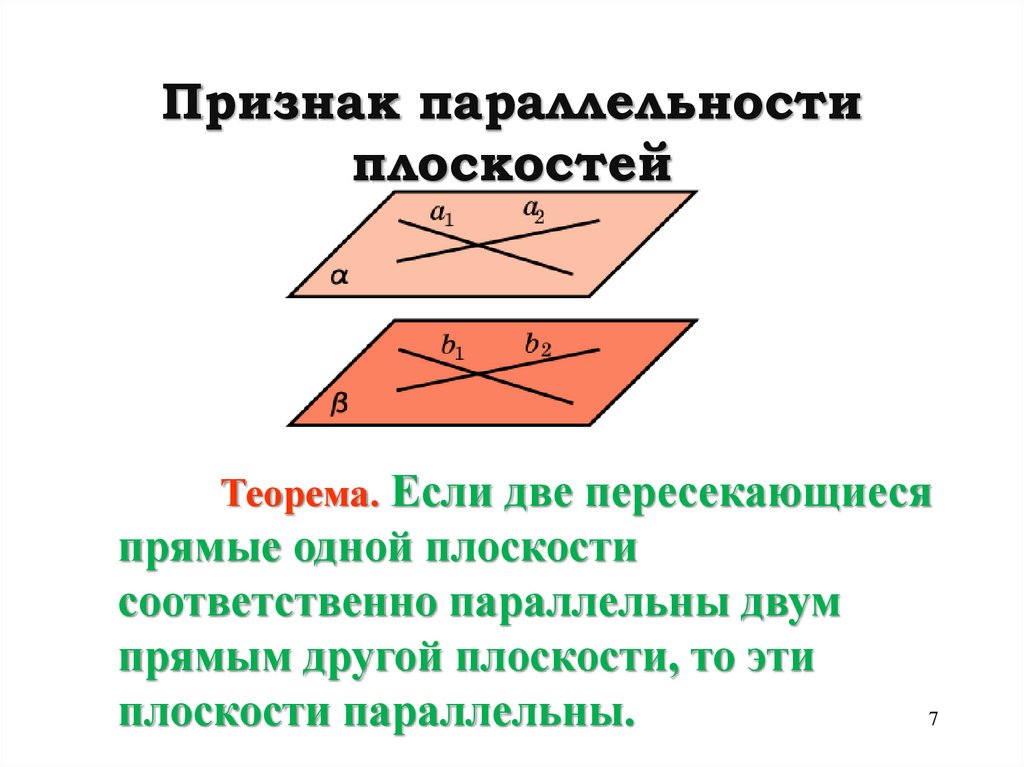
7. Признак параллельности плоскостей
Теорема. Если две пересекающиесяпрямые одной плоскости
соответственно параллельны двум
прямым другой плоскости, то эти
плоскости параллельны.
7
8. Свойства
3. Если прямая пересекает одну изпараллельных
плоскостей,
то
она
пересекает и другую.
4. Если плоскость пересекает одну из
параллельных
плоскостей,
то
она
пересекает и вторую плоскость.
5. В пространстве через точку, не
лежащую на данной плоскости, можно
провести плоскость, параллельную данной,
и притом только одну.
9.
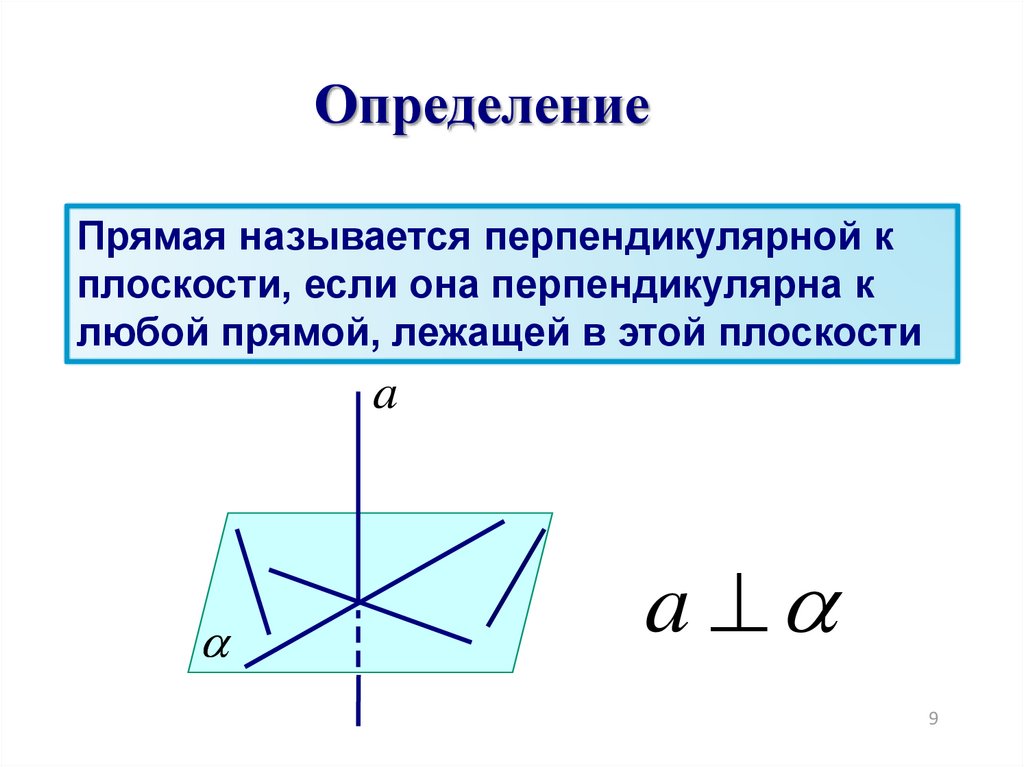
ОпределениеПрямая называется перпендикулярной к
плоскости, если она перпендикулярна к
любой прямой, лежащей в этой плоскости
a
a
9
10.
Признак перпендикулярностипрямой и плоскости
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна к этой
плоскости
a
c
04.06.2020
O
b
a b , a c
b c O
a
10
11.
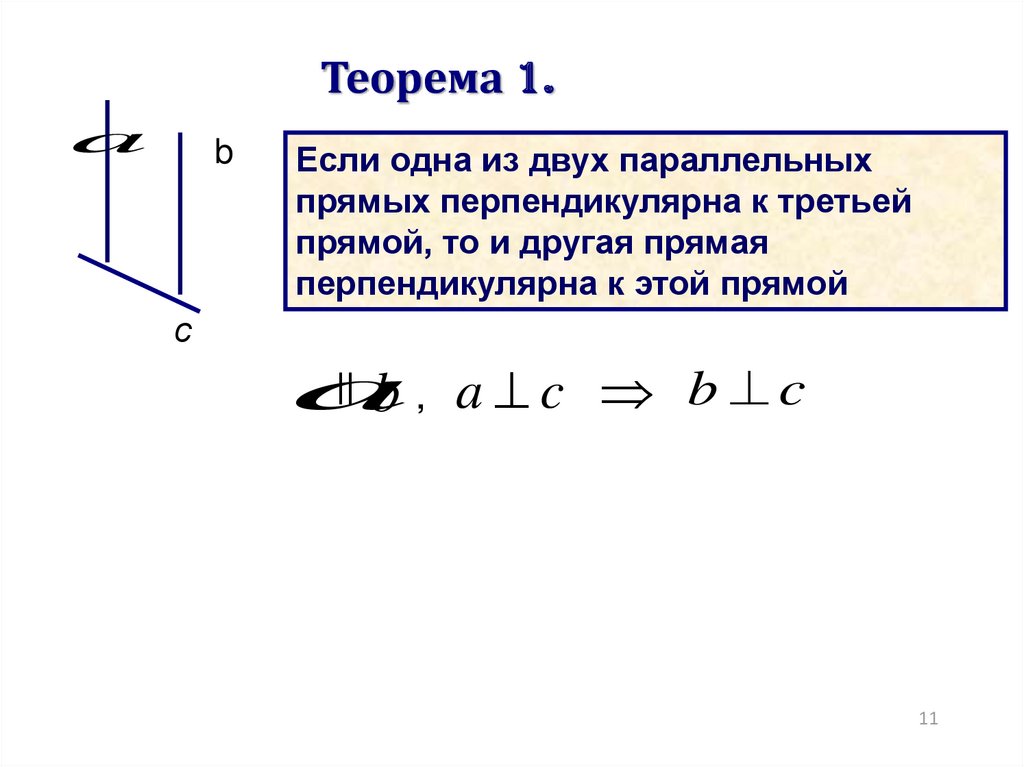
Теорема 1.a
b
Если одна из двух параллельных
прямых перпендикулярна к третьей
прямой, то и другая прямая
перпендикулярна к этой прямой
с
|| b , a c
a
b c
11
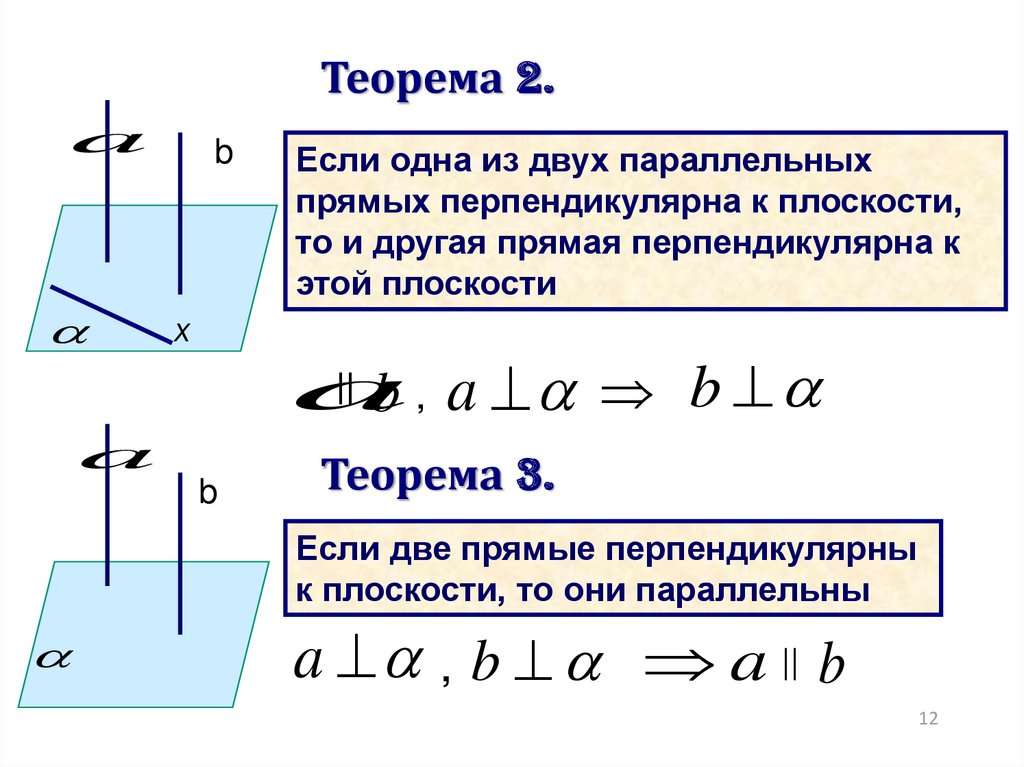
12.
Теорема 2.a
b
х
Если одна из двух параллельных
прямых перпендикулярна к плоскости,
то и другая прямая перпендикулярна к
этой плоскости
|| b , a b
a
a
b
Теорема 3.
Если две прямые перпендикулярны
к плоскости, то они параллельны
a , b a || b
12
13.
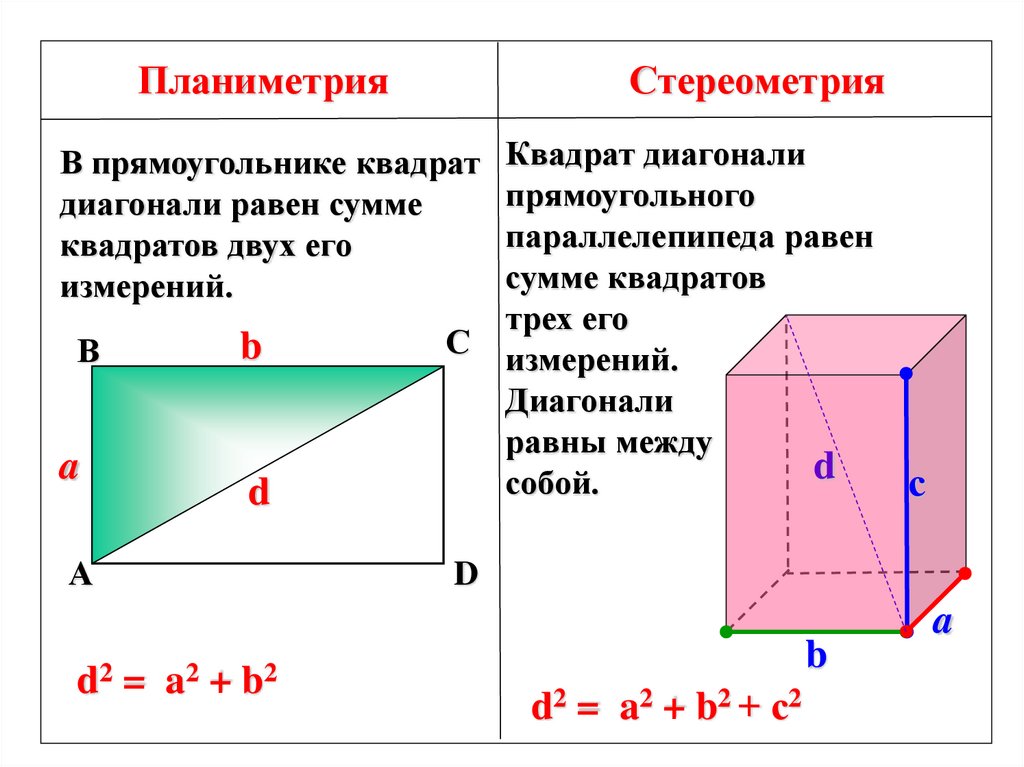
ПланиметрияСтереометрия
В прямоугольнике квадрат
диагонали равен сумме
квадратов двух его
измерений.
В
b
a
d
А
d2
С
Квадрат диагонали
прямоугольного
параллелепипеда равен
сумме квадратов
трех его
измерений.
Диагонали
равны между
d
собой.
с
D
=
a2
+
b2
b
d2 = a2 + b2 + с2
a
14.
Расстоянием от точки до прямой является длинаперпендикуляра
a
N
перпендикуляр
M
H
Н – основание перпендикуляра
N – основание наклонной
HN – проекция
наклонной
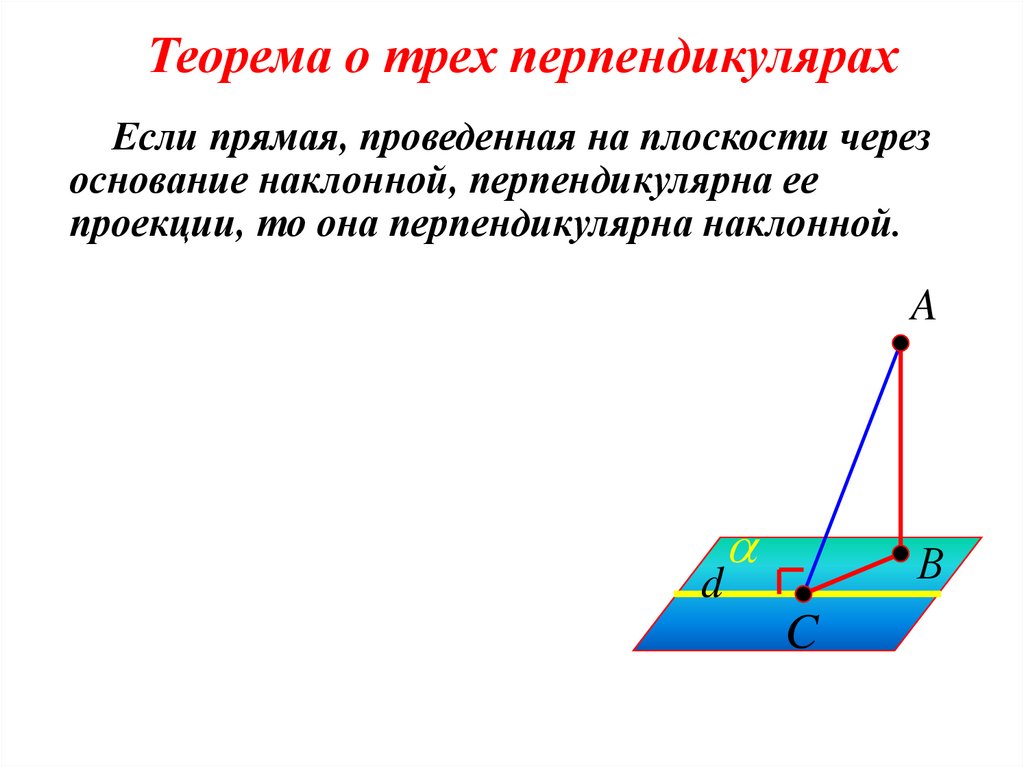
15. Теорема о трех перпендикулярах
Если прямая, проведенная на плоскости черезоснование наклонной, перпендикулярна ее
проекции, то она перпендикулярна наклонной.
A
d
В
C
16.
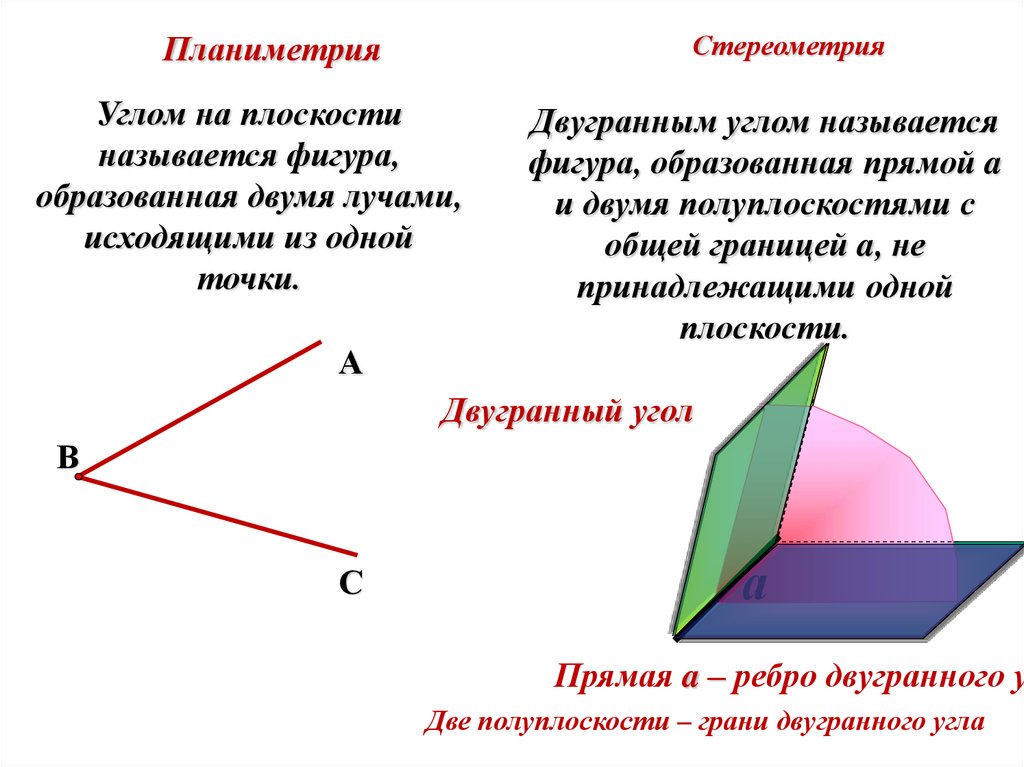
СтереометрияПланиметрия
Углом на плоскости
называется фигура,
образованная двумя лучами,
исходящими из одной
точки.
А
Двугранным углом называется
фигура, образованная прямой a
и двумя полуплоскостями с
общей границей a, не
принадлежащими одной
плоскости.
Двугранный угол
В
С
а
Прямая a – ребро двугранного у
Две полуплоскости – грани двугранного угла
17.
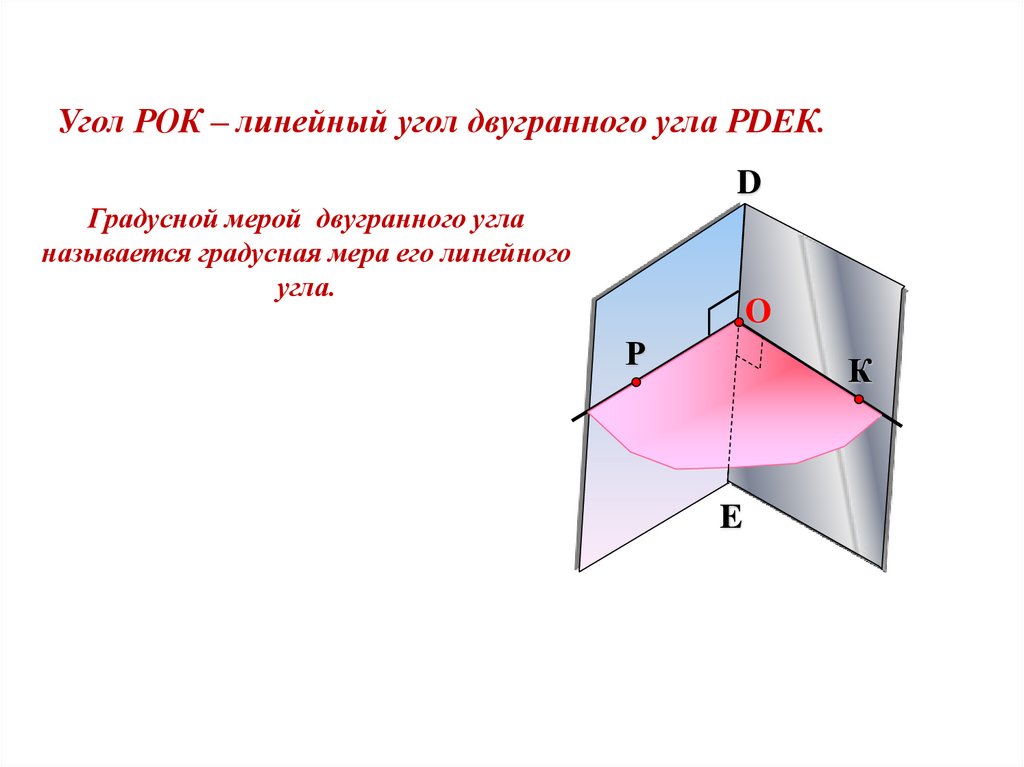
Угол РОК – линейный угол двугранного угла РDEК.D
Градусной мерой двугранного угла
называется градусная мера его линейного
угла.
O
Р
К
E
18.
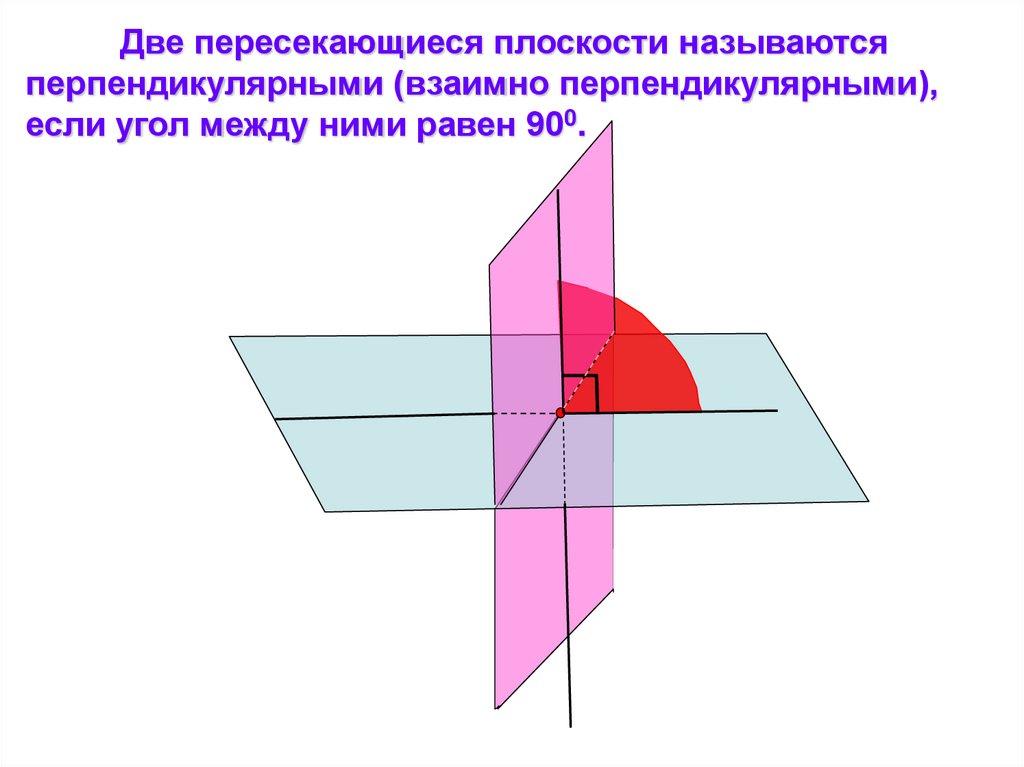
Две пересекающиеся плоскости называютсяперпендикулярными (взаимно перпендикулярными),
если угол между ними равен 900.
19.
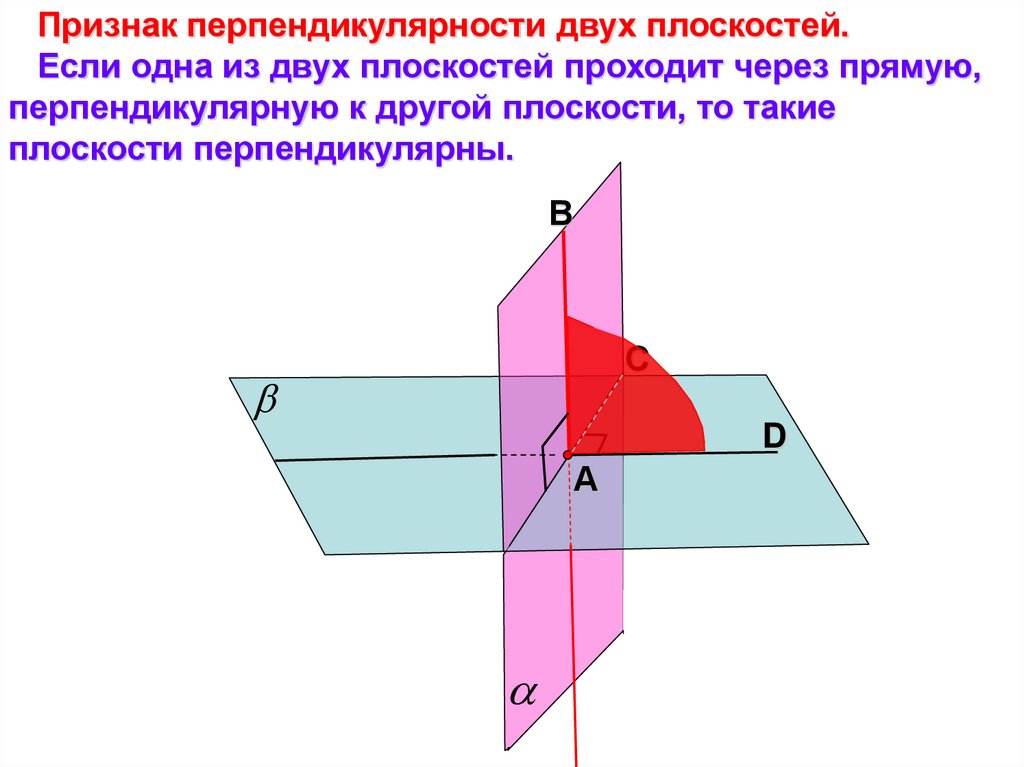
Признак перпендикулярности двух плоскостей.Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
В
С
D
А




 Математика
Математика








