Похожие презентации:
Уравнения состояния термодинамической системы
1. Лекция 11. Уравнения состояния термодинамической системы
Уравнения Клайперона-Менделеева.Идеальный газовый термометр.
Основное уравнение МКТ.
Равномерное распределение энергии по
степеням свободы молекул.
Внутренняя энергия идеального газа.
Эффективный диаметр и средняя длина
свободного пробега молекул газа.
Экспериментальные подтверждения МКТ.
2.
Не бойся, что не знаешь – бойся, что неучишься.
Китайский афоризм
Когда много учишься, то не только лицо,
но и тело приобретает умное выражение.
ФРИДРИХ НИЦШЕ
3. Изобарический процесс. Р = const. Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение
газа при изобарическом процессеподчиняется закону Гей-Люссака:
V1 V2
V/T = const
T1
2020 г. Чуев А.С.
T2
3
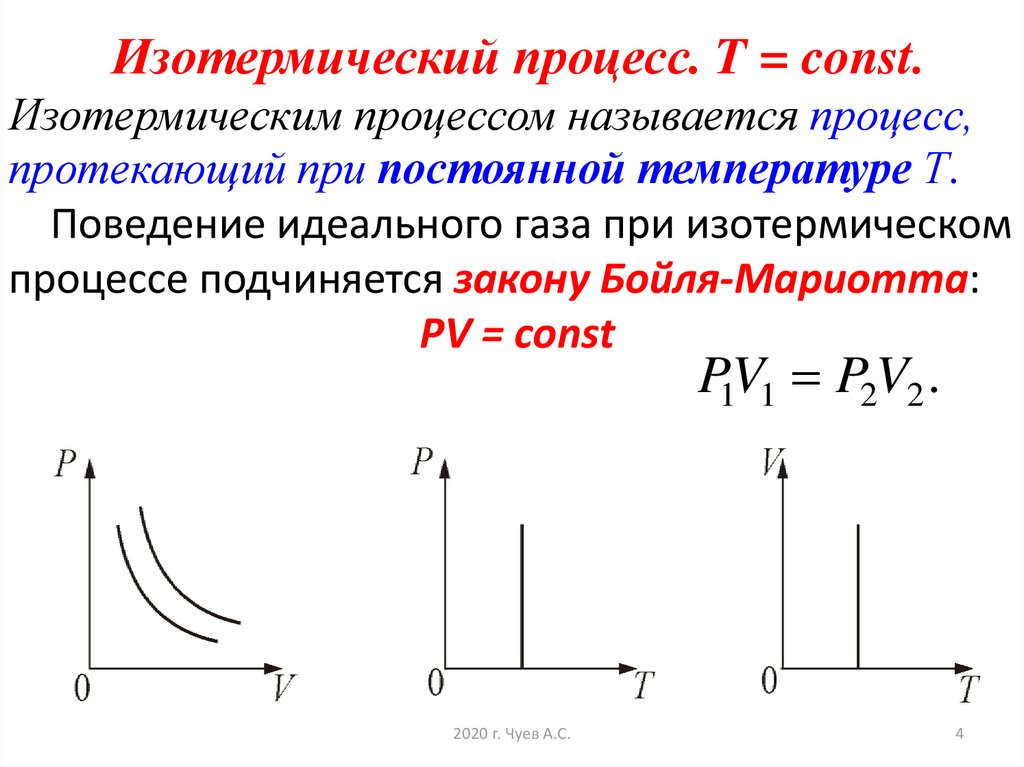
4. Изотермический процесс. T = const. Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа при изотермическомпроцессе подчиняется закону Бойля-Мариотта:
РV = const
P1V1 P2V2 .
2020 г. Чуев А.С.
4
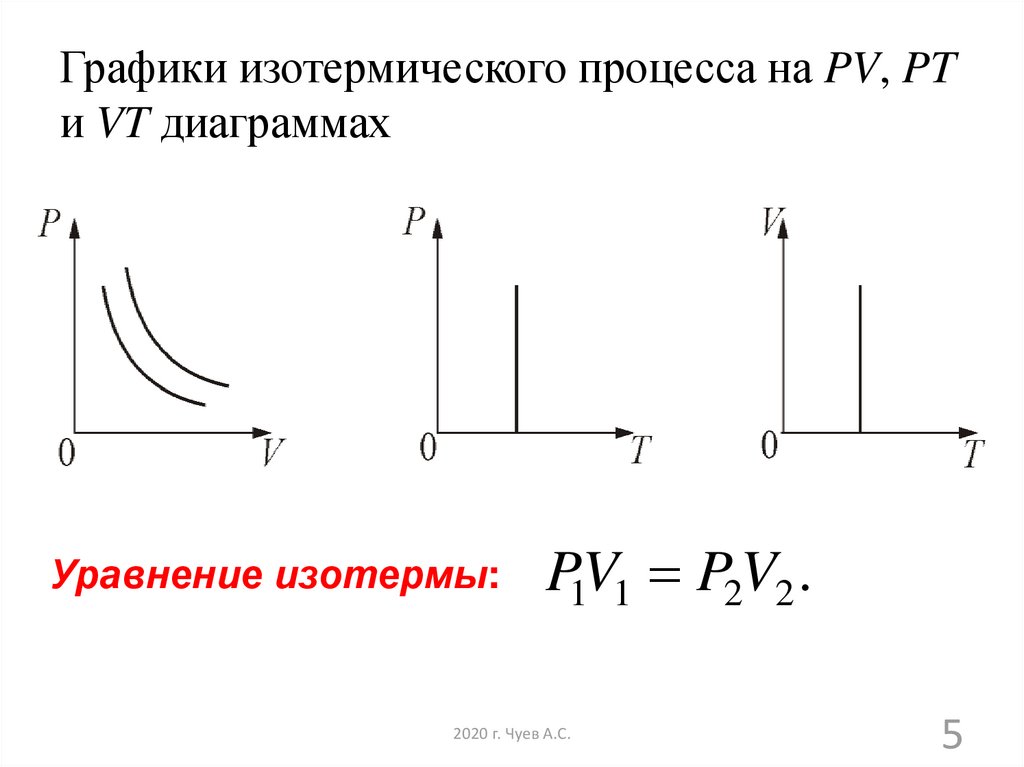
5. Графики изотермического процесса на PV, PT и VT диаграммах
Уравнение изотермы:P1V1 P2V2 .
2020 г. Чуев А.С.
5
6. Объединённый газовый закон (Закон Клапейрона). Совместив законы Бойля – Мариотта и Гей-Люссака можно получить, что для данной
Объединённый газовый закон(Закон Клапейрона).
Совместив законы Бойля – Мариотта и ГейЛюссака можно получить, что для данной
массы газа
P1V1 P2V2
или
T1
T2
PV
const.
T
Это объединённый газовый закон
Клапейрона.
2020 г. Чуев А.С.
6
7. Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с законом Авогадро. Уравнение, связывающее все эти
законы, называется уравнением МенделееваКлапейрона и записывается так:m
PV RT
μ
m
здесь μ – число молей. Для одного моля можно
записать
PVμ RT
2020 г. Чуев А.С.
7
8. Если обозначить – плотность газа, то Если рассматривать смесь газов, заполняющих объём V при температуре Т, тогда можно найти
mρ
Если обозначить V
– плотность газа, то
m
ρ
P
RT RT .
μV
μ
Если рассматривать смесь газов,
заполняющих объём V при температуре Т,
тогда можно найти парциальные давления:
m1RT
P1
μ1V,
m2 RT
P2
μ 2,V…..
2020 г. Чуев А.С.
mn RT
Pn
μ nV
8
9. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов (Рi – давление, которое
Закон Дальтона.Давление смеси идеальных газов равно сумме
парциальных давлений Р, входящих в неё газов
Pсм P1 P2 ... Pn
(Рi – давление, которое оказывал бы определённый
газ из смеси, если бы он занимал весь объём).
m1RT m2 RT RT m1 m2
Pñì
.
μ1V
μ 2V
V μ1 μ 2
2020 г. Чуев А.С.
9
10. Так как согласно закону Дальтона: можно записать – это уравнение Менделеева-Клапейрона для смеси газов.
Так как согласно закону Дальтона:P P1 P2 ... Pn
можно записать
m1 m2
mn
PV
... RT
μn
μ1 μ 2
– это уравнение Менделеева-Клапейрона
для смеси газов.
2020 г. Чуев А.С.
10
11.
Термометры. Единица измерениятемпературы.
Наиболее естественно было бы использовать
для измерения температуры определение
1 m0 v
T
3
2
2
т.е. измерять среднюю кинетическую энергию
поступательного движения молекул газа. Однако
это невозможно. Поэтому для определения
температуры идеального газа используется
уравнение
PV m/ μ RT.
2020 г. Чуев А.С.
11
12. Действительно, величины P и V легко поддаются измерению. В качестве примера рассмотрим изображенный на рисунке простейший
газовый термометр с постояннымдавлением.
nk
T
Объем газа в трубке V
P0
пропорционален температуре, а
поскольку высота подъема ртутной
капли пропорциональна V, то она
пропорциональна и Т.
2020 г. Чуев А.С.
12
13.
Идеальный газовый термометр2020 г. Чуев А.С.
13
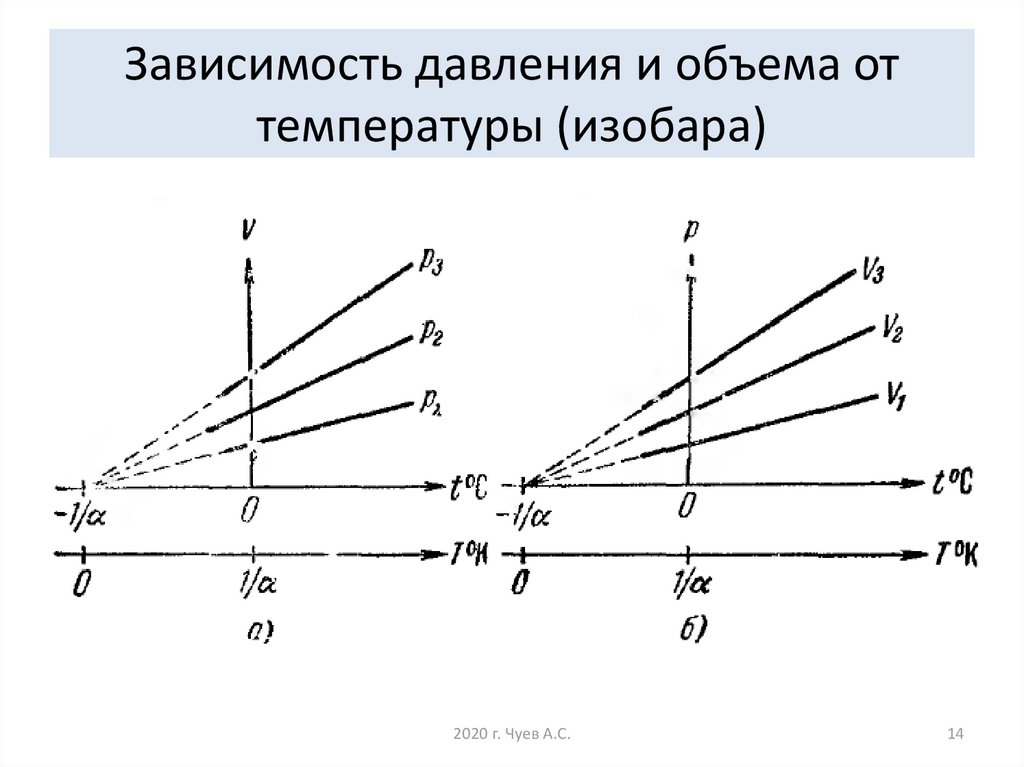
14. Зависимость давления и объема от температуры (изобара)
2020 г. Чуев А.С.14
15. Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде где - температурный
Если температура газа выражена в градусахЦельсия, то уравнение изобарического процесса
записывается в виде
V V0 1 αt ,
где α 1 / 273 град 1 - температурный
коэффициент объёмного расширения.
2020 г. Чуев А.С.
15
16. В физике и технике за абсолютную шкалу температур принята шкала Кельвина, названная в честь знаменитого английского физика,
лордаКельвина.
1 К – одна из основных единиц системы СИ
Кроме того, используются и другие шкалы:
– шкала Фаренгейта (немецкий физик 1724 г.) –
точка таянья льда 32 F, точка кипения воды 212 F.
– шкала Цельсия (шведский физик 1842г.) – точка
таянья льда 0 С, точка кипения воды 100 С.
0 С = 273,15 К.
2020 г. Чуев А.С.
16
17.
2020 г. Чуев А.С.17
18. Так как всегда, то и Т не может быть отрицательной величиной. Своеобразие температуры заключается в том, что она не аддитивна
mυ0 всегда, то и Т не
Так как
2
может быть отрицательной величиной.
2
Своеобразие температуры заключается в
том, что она не аддитивна (аддитивный –
получаемый сложением).
Если мысленно разбить тело на части, то
температура всего тела не равна сумме температур
его частей (длина, объём, масса, сопротивление, и
так далее – аддитивные величины).
Поэтому температуру нельзя измерять, сравнивая
её с эталоном.
2020 г. Чуев А.С.
18
19.
ОСНОВНОЕ УРАВНЕНИЕМОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ
ТЕОРИИ
(выражение через температуру)
20.
2020 г. Чуев А.С.20
21.
Слайд прошлой лекцииДля молекул, имеющих скорость
получим:
2020 г. Чуев А.С.
21
22. Основное уравнение молекулярно-кинетической теории газов иллюстрирует: давление газов определяется средней кинетической
Прошлая лекция:Основное уравнение молекулярнокинетической теории газов иллюстрирует:
давление газов определяется средней
кинетической энергией поступательного
движения молекул и их плотностью.
2020 г. Чуев А.С.
22
23. Основное уравнение молекулярно-кинетической теории можно записать через температуру. Так как Отсюда Другая запись основного
Основное уравнение молекулярнокинетической теории можно записатьчерез температуру. Так как
P 2 / 3n Ek ,
Отсюда
Ek 3 / 2kT
P nkT
Другая запись основного уравнения
молекулярно-кинетической теории.
(Употребляется чаще).
2020 г. Чуев А.С.
23
24. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ МОЛЕКУЛ ПО СТЕПЕНЯМ СВОБОДЫ МОЛЕКУЛ
2020 г. Чуев А.С.24
25. Числом степени свободы называется число независимых переменных, определяющих положение тела в пространстве и обозначается i i =
Числом степени свободы называется числонезависимых переменных, определяющих положение
тела в пространстве и обозначается i
i=3
Положение материальной точки (одноатомной
молекулы) задаётся тремя координатами, поэтому она
имеет три степени свободы: i = 3
2020 г. Чуев А.С.
25
26. Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два
независимых вращения, а любое произвольноевращение можно разложить на три вращательных
движения вокруг 3-х взаимно перпендикулярных
осей.
Но для двухатомных молекул вращение вокруг оси x не
изменит её положение в пространстве, а момент инерции
относительно этой оси равен нулю
(см. следующий рисунок).
2020 г. Чуев А.С.
26
27.
Типы простейших молекул2020 г. Чуев А.С.
27
28.
Сложная молекула2020 г. Чуев А.С.
28
29.
У двухатомных молекул пять степеней свободы i = 5,у трёхатомных шесть степеней свободы
i = 6.
i=3
i=5
2020 г. Чуев А.С.
i=6
29
30. При взаимных столкновениях молекул возможен обмен их энергиями и превращение энергии вращательного движения в энергию
поступательногодвижения и обратно.
Таким путём устанавливается равновесие
между значениями средних энергий
поступательного и вращательного движений
молекул.
2020 г. Чуев А.С.
30
31. Больцман обосновал, что, средняя энергия, приходящаяся на одну степень свободы равна
Гипотеза о равномерном распределенииэнергии по степеням свободы
Больцман обосновал, что, средняя энергия,
приходящаяся на одну степень свободы
равна 1 kT .
2
1
K kT .
2
2020 г. Чуев А.С.
31
32. На среднюю кинетическую энергию молекулы, имеющей i-степеней свободы приходится Это и есть закон Больцмана о равномерном
На среднюю кинетическую энергиюмолекулы, имеющей i-степеней свободы
приходится
i
K kT
2
Это и есть закон Больцмана о равномерном
распределении средней кинетической энергии по
степеням свободы.
Здесь
i = iп + iвр + 2iкол
2020 г. Чуев А.С.
32
33.
i iпост iв ращ 2iколеб2020 г. Чуев А.С.
33
34.
2020 г. Чуев А.С.34
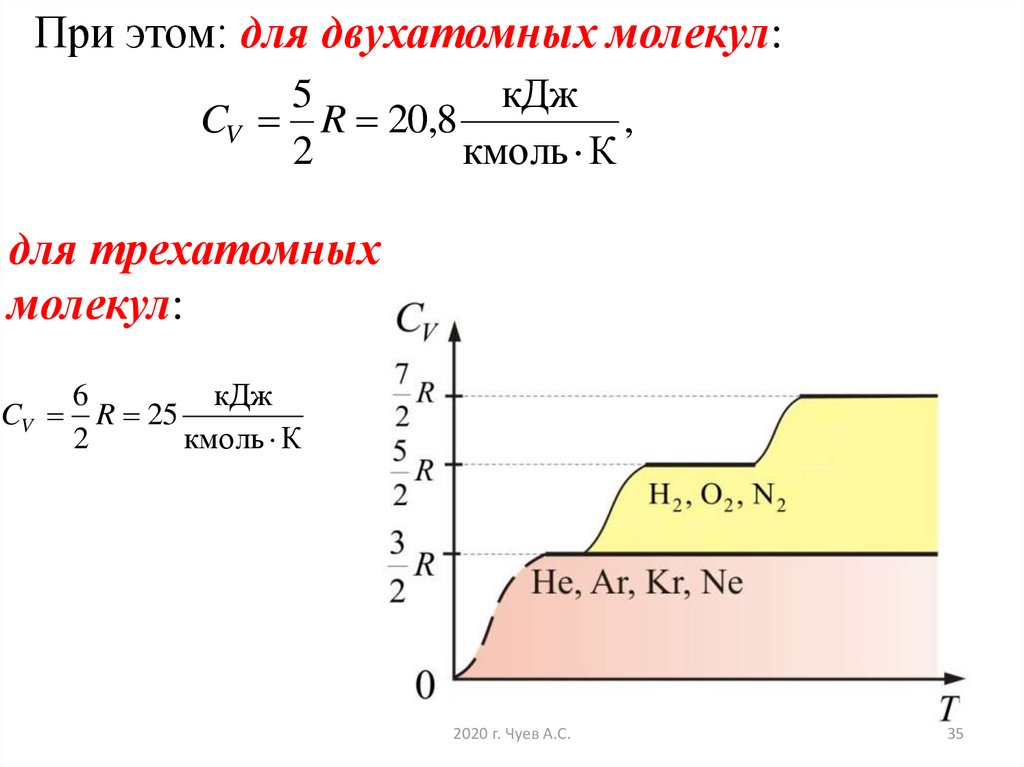
35. для трехатомных молекул:
При этом: для двухатомных молекул:5
кДж
CV R 20,8
,
2
кмоль К
для трехатомных
молекул:
CV
6
кДж
R 25
2
кмоль К
2020 г. Чуев А.С.
35
36.
2020 г. Чуев А.С.36
37.
Явление температурного резонансатеплоемкости
2020 г. Чуев А.С.
37
38.
2020 г. Чуев А.С.38
39.
2020 г. Чуев А.С.39
40.
Эффективный диаметр и средняядлина свободного пробега молекул
Минимальное расстояние, на которое
сближаются при столкновении центры
двух молекул, называется эффективным
диаметром
Эффективное
сечение
молекулы
2020 г. Чуев А.С.
40
41.
σ– эффективное сечение молекулы. Оно
больше площади круга с ее диаметром
σ πd
2
– площадь в которую не может
проникнуть центр любой другой молекулы.
2020 г. Чуев А.С.
41
42. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега: – средняя скорость
Расстояние, проходимое молекулой всреднем без столкновений, называется
средней длиной свободного пробега:
vср ,
v ср – средняя скорость теплового движения, τ –
среднее время между двумя столкновениями.
2020 г. Чуев А.С.
42
43.
λi2020 г. Чуев А.С.
43
44. За одну секунду молекула проходит путь, равный средней арифметической скорости За ту же секунду молекула претерпевает ν
За одну секунду молекула проходит путь,равный средней арифметической скорости
v
За ту же секунду молекула претерпевает ν
столкновений. Поэтому средняя длина свободного
пробега молекулы:
v
ν
2020 г. Чуев А.С.
44
45.
Путь, который пройдетмолекула за одну секунду, равен
длине цилиндра v'
v'
- объём цилиндра
n - число молекул в единице объёма
v'
среднее число столкновений в одну секунду:
ν πd v' n.
2
2020 г. Чуев А.С.
45
46.
С учетом разнонаправленности скоростейТогда средняя длина свободного пробега молекул без
столкновений
v
ν
2020 г. Чуев А.С.
46
47. Из уравнения состояния идеального газа выразим n через давление P и температуру Т Так как , то есть тогда
Из уравнения состояния идеального газавыразим n через давление P и температуру Т
P
Так как P nkT , то есть n
, тогда
kT
kT
kT
λ
.
2
2πd P
2σP
2020 г. Чуев А.С.
47
48.
Опыт Штерна, 1920 г.Время пролета
Нить из Ag
Сила Кориолиса
2020 г. Чуев А.С.
48
49. Температура нити в опытах Штерна равнялась 1200С, что соответствует среднеквадратичной скорости молекул серебра В эксперименте
Температура нити в опытах Штернаравнялась 1200 С, что соответствует
среднеквадратичной скорости молекул
серебра
v 584 м/с
кв
В эксперименте получился разброс значений
скорости от 560 до 640 м/с. Кроме того,
изображение щели D всегда оказывалось
размытым, что указывало на то, что атомы Ag
движутся с различными скоростями.
2020 г. Чуев А.С.
49
50. Опыт Ламмерта, 1929 г.
2020 г. Чуев А.С.50
51. Конец 11 лекции
2020 г. Чуев А.С.51














































 Физика
Физика








