Уравнения состояния термодинамических систем

1. Лекция № 11

УРАВНЕНИЯ СОСТОЯНИЯ
ТЕРМОДИНАМИЧЕСКИХ
СИСТЕМ
Лекции Веретимус Н.К. и Веретимус Д.К.

2. Литература:

•Глаголев К.В., Морозов А.Н. Физическая
термодинамика: Учеб. пособие. – М.: Изд-во
МГТУ им. Н.Э.Баумана, 2004. – 368 с./Под
ред. Л.К.Мартинсона, А.Н.Морозова.
•Иродов И.Е. Физика макросистем. Основные
законы. – М.: Лаборатория Базовых Знаний,
2001

3. Уравнение состояния идеального газа

(уравнение Менделеева-Клапейрона):
m
pV RT RT ,
(11.1)
где R 8,314 Дж моль К – универсальная
газовая постоянная, μ – молярная масса
газа, μ=[кг/моль]; m – масса газа, m=[кг];
ν= m/μ – количество вещества, ν =[моль].
В дальнейшем в качестве системы
рассматривается идеальный газ.

4.

Моль – количество вещества, содержащее
число частиц, равное постоянной Авогадро:
23
1
N A 6,022 10 моль .
Молярная масса – масса одного моля.
Объединенный газовый закон. Для
данного количества вещества
const
pV
const
T
(11.1а)
Изопроцессы проходят при постоянном
количестве вещества ν и при постоянстве
одного из параметров состояния газа (p, V, T).

5.

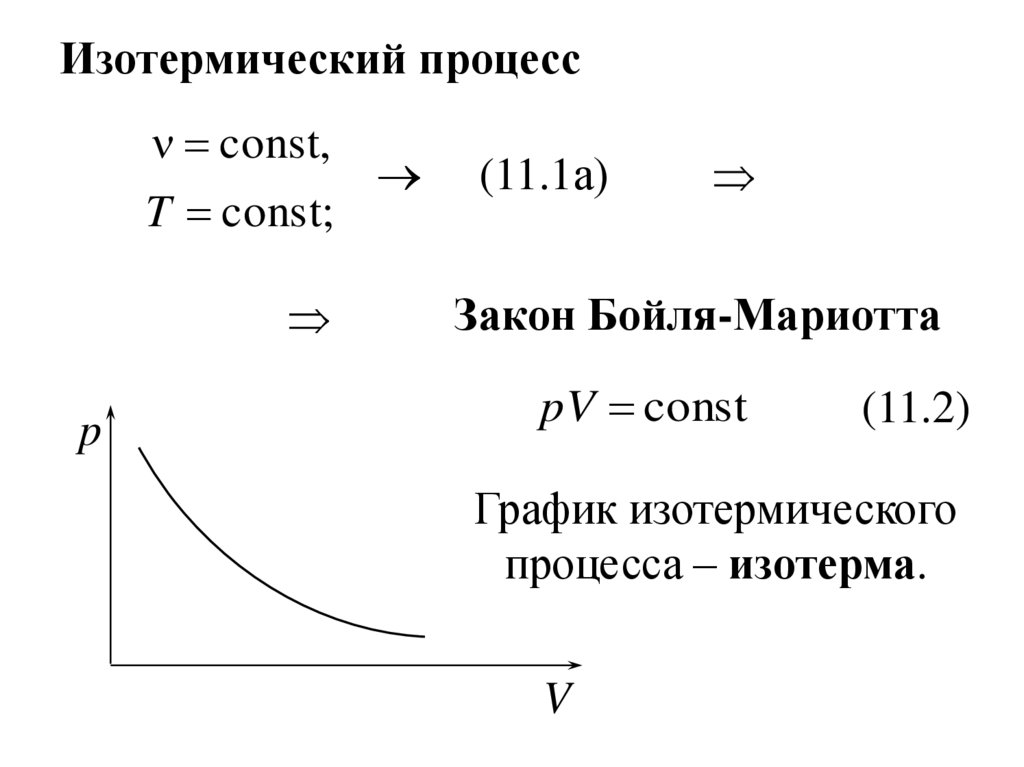
Изотермический процесс
const,
T const;
p
(11.1а)
Закон Бойля-Мариотта
pV const
(11.2)
График изотермического
процесса – изотерма.
V

6.

Изобарический (изобарный) процесс
const,
p const;
(11.1а)
Закон Гей-Люссака
V
const
T
p
(11.3)
График – изобара.
V

7.

Изохорический (изохорный) процесс
const,
V const;
(11.1а)
Закон Шарля
p
const
T
p
(11.4)
График – изохора.
V

8.

Существуют и другие стандартные
процессы, в которых сохраняется какая-либо
термодинамическая величина, которые, хотя
и не являются изопроцессами, весьма важны:
адиабатный и политропный процессы.
Идеально-газовый термометр
Самостоятельно. Глаголев К.В., Морозов
А.Н. Физическая термодинамика: Учеб.
пособие.– М.: Изд-во МГТУ им. Н.Э.Баумана,
2004. – 368 с./Под ред. Л.К.Мартинсона,
А.Н.Морозова. Параграф 1.3 (с. 15-19).

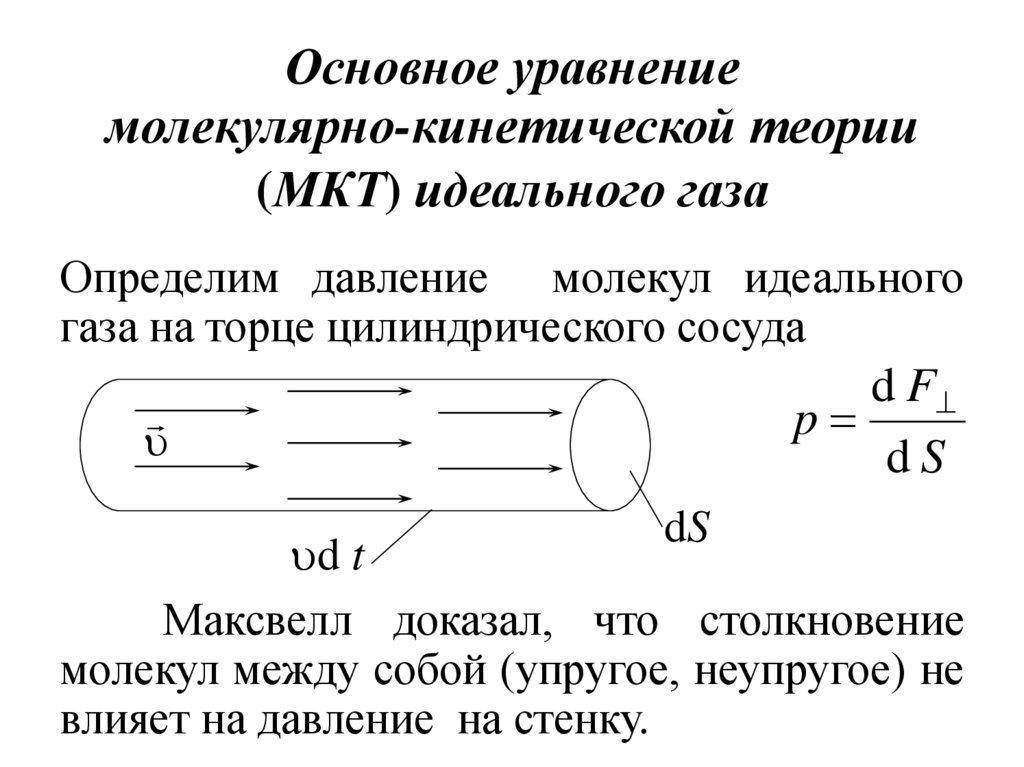
9. Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа

Определим давление молекул идеального
газа на торце цилиндрического сосуда
d F
p
dS
dS
d t
Максвелл доказал, что столкновение
молекул между собой (упругое, неупругое) не
влияет на давление на стенку.

10.

Допущение: пусть все молекулы,
находящиеся в сосуде, движутся с одной и
той же скоростью и 1/6 их часть летит к
стенке ( стенке). При упругом ударе о
стенку, масса которой бесконечно велика,
приращение импульса каждой молекулы в
результате столкновения
F
p p2 p1 2m0 ,
p1
p2
x
где m0 – масса одной молекулы, – скорость.

11.

1 1
d F p n d S d t 1
2
2
m
n
m0n ,
0
p
6 3
dS
d S dt
6
где n – концентрация молекул (число
молекул в единице объема). Здесь
p
d F d Fx
.
t
Т.к. скорости отдельных молекул υi
могут быть различными, то величину nυ2
следует
заменить
суммой
квадратов
скоростей каждой из молекул, находящихся в
единице объема:

12.

2
2
2
2
2
2
2
...
n 2
...
1
2 3
n
n раз
n
2
i 1
n раз
2
i
n
n
2 ; кв.
i 1
2
i
n
,
где υкв. – средняя квадратичная скорость.
1
p m0 n кв2.
(11.5)
3
m0 кв2.
пост .
2
–
средняя
энергия
поступательного движения
молекулы.

13.

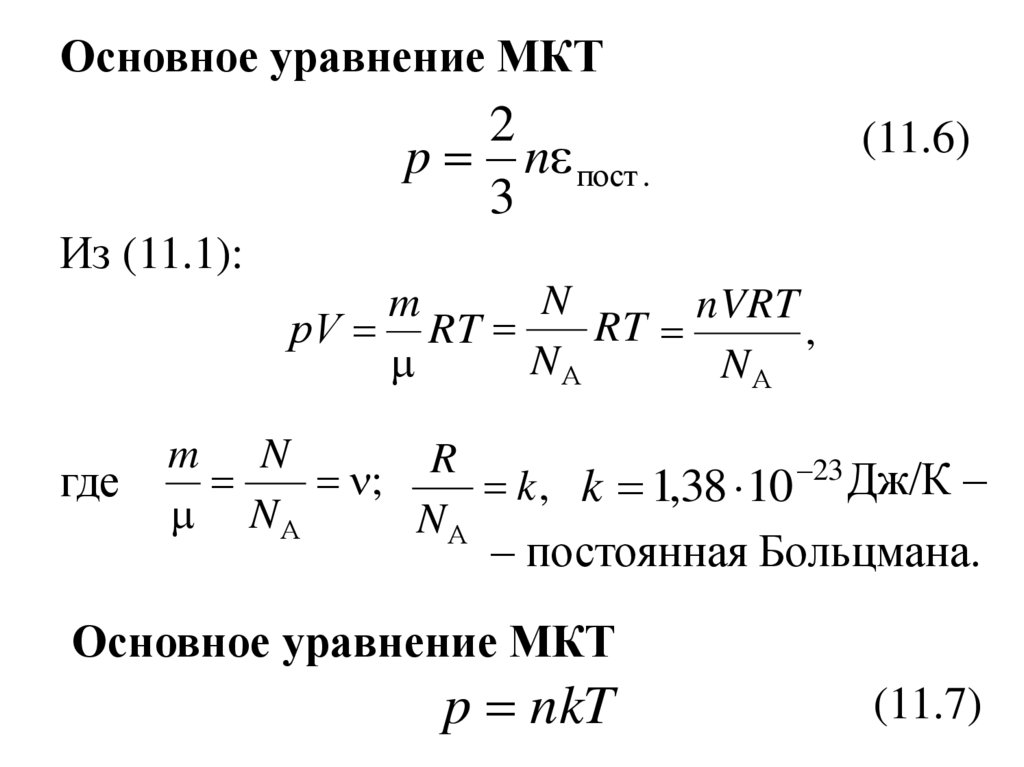
Основное уравнение МКТ
2
p n пост .
3
(11.6)
Из (11.1):
N
m
nVRT
RT
рV RT
,
NА
NА
где
m N
R
;
k , k 1,38 10 23 Дж/К –
NА
NА
– постоянная Больцмана.
Основное уравнение МКТ
p nkT
(11.7)

14.

Из (11.6) и (11.7)
3
(11.8)
пост . kT
2
(11.8) вскрывает физический смысл
температуры T: температура выражает
среднюю кинетическую энергию молекул.
Считая все молекулы газа одинаковыми
и имеющими массу m0
m0 кв2. 3
пост .
kT ,
2
2

15.

2
кв .
2
2 Ek 2 пост .
3
kT ,
m0
m0
m0
2
средняя квадратичная скорость
кв
3kT
m0
2
(11.9)

16. Равномерное распределение энергии по степеням свободы молекул

Согласно
(11.8)
средняя
энергия
поступательного движения молекулы
3
пост . kT
2
iпост.=3. На каждую степень свободы i в
среднем
приходится
энергия
kT/2.
Больцманом предложена гипотеза о равном
распределении
средней
энергии
по
степеням свободы:
kT
I
2
(11.10)

17.

Средняя энергия молекулы
ikT
,
2
(11.11)
где i – сумма числа поступательных (iпост.),
вращательных (iвр.) и удвоенного числа
колебательных (iкол.) степеней свободы:
i iпост . iвр. 2iкол.
(11.12)
i совпадает с числом степеней свободы только
для жестких молекул.

18.

Для жесткой молекулы:
одноатомной
1 ат .
3
kT
2
двухатомной
2 x ат .
5
kT
2
трехатомной
3x ат .
6
kT 3kT
2

19. Внутренняя энергия идеального газа

Т.к. частицы идеального газа между
собой не взаимодействуют, то внутренняя
энергия частиц:
mi
i
U kT N А
RT ,
2
2
где ikT/2 – энергия одной частицы, m/μ=ν –
количество вещества.
i
U RT ,
(11.13)
2
i
dU R d T
(11.14)
2
При изотермическом
d T 0 dU 0
процессе

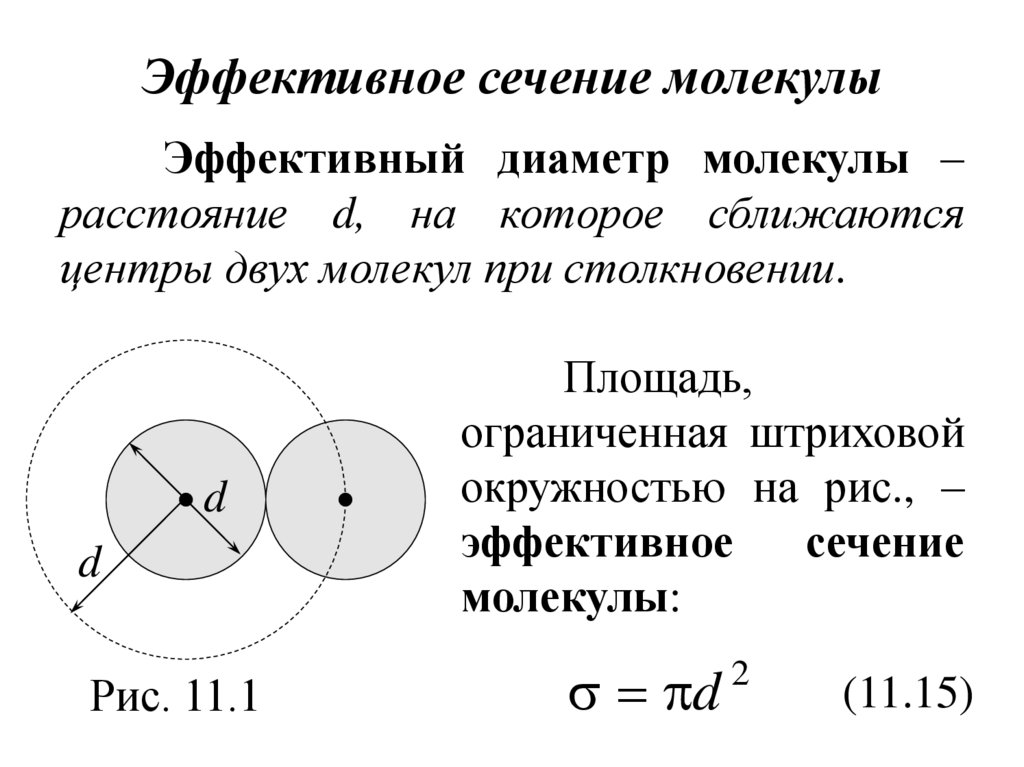
20. Эффективное сечение молекулы

Эффективный диаметр молекулы –
расстояние d, на которое сближаются
центры двух молекул при столкновении.
d
d
Рис. 11.1
Площадь,
ограниченная штриховой
окружностью на рис., –
эффективное
сечение
молекулы:
d
2
(11.15)

21. Среднее число соударений и средняя длина свободного пробега молекул

Длина свободного пробега молекулы –
среднее расстояние, проходимое молекулой
между
двумя
последовательными
столкновениями ее с другими молекулами.
За секунду молекула проходит в среднем
путь, равный ее средней скорости
.
Если при этом она претерпевает в среднем z
столкновений, то средняя длина свободного
пробега молекулы
(11.16)
z

22.

Определим z, проследив за поведением
молекулы, движущейся плоскости рисунка
(рис. 11.1).
За единицу времени она столкнется со
всеми молекулами, центры которых окажутся
в пределах объема цилиндра радиуса d. При
каждом
столкновении
цилиндр
будет
испытывать «излом». Объем V такого
«ломаного» цилиндра (при λ >> d):
V d
2
(11.17)
При λ >> d можно пренебречь частями объема
цилиндра, приходящимися на его изломы.

23.

Тогда среднее число
молекулы ежесекундно:
z Vn n,
столкновений
(11.18)
где n – концентрация молекул.
Средняя длина свободного пробега
молекул газа из (11.16) равна
1
n
(11.19)

24.

При более строгом рассмотрении
вопроса о числе столкновений z, необходимо
заменить среднюю скорость <υ> на среднюю
относительную скорость
отн 2
Уточненные формулы (11.18) и (11.19):
z 2 n,
где
d .
2
1
,
2 n
(11.20)

25. Экспериментальные подтверждения МКТ

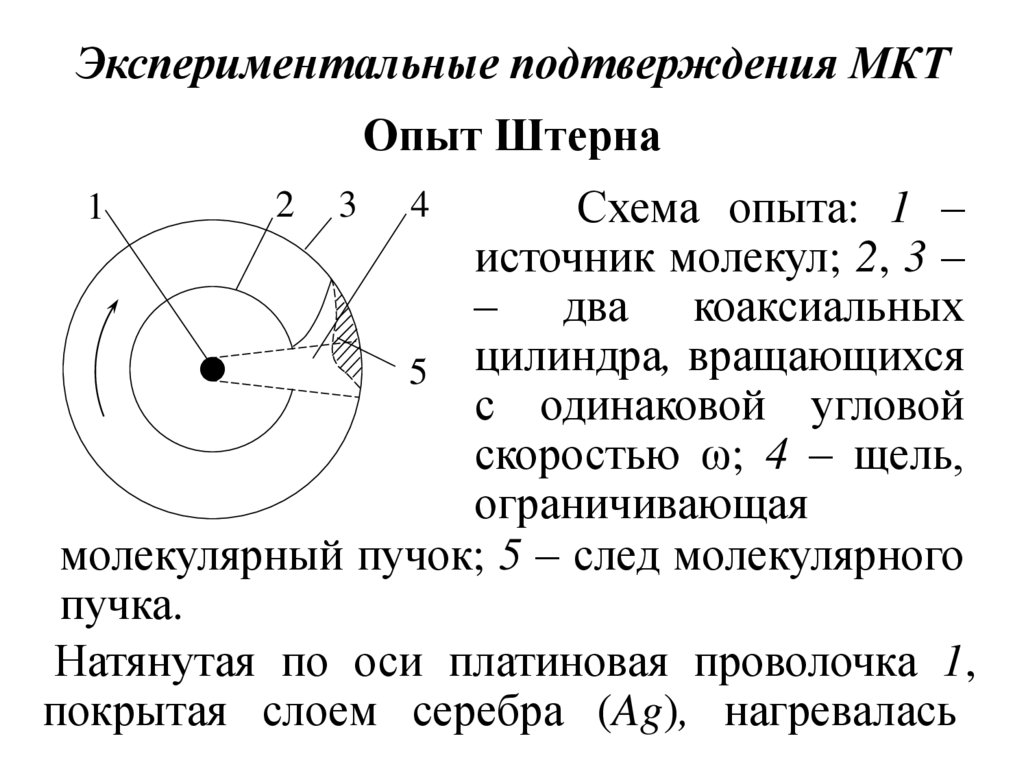
Опыт Штерна
Схема опыта: 1 –
источник молекул; 2, 3 –
– два коаксиальных
5 цилиндра, вращающихся
с одинаковой угловой
скоростью ω; 4 – щель,
ограничивающая
молекулярный пучок; 5 – след молекулярного
пучка.
Натянутая по оси платиновая проволочка 1,
покрытая слоем серебра (Ag), нагревалась
1
2
3
4

26.

электрическим током до t = 1200° C, при
которой атомы Ag испарялись. Воздух из
установки предварительно откачивали, чтобы
летящие атомы Ag не сталкивались с
молекулами воздуха.
Через
узкую
прорезь
4
вдоль
внутреннего цилиндра 2 вылетает пучок
атомов Ag, скорости которых направлены
радиально.
Пока атом Ag, летящий со скоростью υ,
проходит расстояние между цилиндрами l,
цилиндры успевают
l
повернуться на угол

27.

Прошедшие через щель 4 атомы Ag
осаждаются на холодной стенке внешнего
цилиндра 3, образуя серебряную полоску 5,
которая представляет собой изображение
щели внутреннего цилиндра на внешнем,
сдвинутое на угол φ. Измерив φ, находят
скорость теплового движения атомов Ag :
l
и сравнивают экспериментальное значение с
выведенным из МКТ.

28.

Прибор
Штерна
совершал
45
об/с.
Совпадение измеренных значений скоростей
молекул с теоретическими было хорошим.
Вследствие
хаотичности
теплового
движения скорости отдельных атомов Ag
несколько отличались друг от друга, в
результате серебряная полоска на внешнем
цилиндре оказалась размазанной, а различная
толщина отложившегося на ней серебра при
разных значениях φ указывает на то, что
некоторые значения скорости молекул
встречаются чаще, а другие – реже.

29.

Анализируя
плотность
осевших
молекул,
можно
было
оценить
характеристики распределения молекул по
скоростям, в частности максимальную и
минимальную скорости, соответствующие
краям следа, а также найти наиболее
вероятную
скорость,
соответствующую
максимальной плотности осевших молекул.
При температуре нити 1200° C среднее
значение
скорости
атомов
серебра,
полученное после обработки результатов
опыта Штерна, оказалось около 600 м/с, что
соответствует
средней
квадратичной
скорости, вычисленной по формуле (11.9).