Похожие презентации:
Решение логарифмических неравенств
1. Тема:
«Решениелогарифмических
неравенств»
2. Цель урока:
• Обобщить теоретическиезнания по теме «Решение
логарифмических неравенств»
• Рассмотреть методы
выполнения заданий на
решение логарифмических
неравенств.
3.
Определение:Логарифмическими
неравенствами называют
неравенства вида
log
a
f ( x) log g ( x)
a
где а – положительное число,
отличное от 1, и неравенства,
сводящиеся к этому виду.
4. Алгоритм
• При а > 1• При 0 < a < 1
f ( x) 0,
g ( x) 0, .
f ( x) g ( x),
f ( x) 0,
g ( x) 0, .
f ( x) g ( x).
5.
log (2x 4) log (14 x)3
3
Решение:
2 x 4 0
14 x 0
2 x 4 14 x
6.
log1
3
(2 x 3) log 1 (14 x)
3
Решение:
2 x 4 0
14 x 0
2 x 4 14 x
7.
log1
2
(16 4 x x ) 4
2
1
2
Решение:
1
4 log log 16
2
4
1
2
1
2
2
(
16
4
x
) log 1 16
x
log 1
2
16 4 х х2 0
2
16
4
x
16
x
2
16 4 x x2 16
x(4 x) 0
0 x 4
8. Область определения:
№1
2
3
Формула
Условия
y log a f ( x)
f ( x) 0
y log g ( x) b
g ( x) 0;
g ( x ) 1.
y log g ( x) f ( x)
g ( x) 0;
g ( x) 1;
f ( x ) 0.
9. Задание 1
1)2)
log
2
log
2
x 4
x 3
3)
1
log2 x 2
4)
1
log2 x 2
10. Задания 2
• 1)• 2)
2
log 1 ( x 7) 3
8
log (3 2x) log 13 0
2
• 3)
log ( x 1) 1 log 2
3
• 4)
2
3
3
log 1 ( x 2) log9 ( x 2) 2
3
11.
• 1)log (5x 9) log (3x 1)
• 2)
lg( x 8) lg( 2 9 x)
• 3)
2
2
2
log ( x
2
2
6 x 24) 4
12. Самостоятельная работа
• 1)• 2)
• 3)
log
2
2
2
x 4 log x 3
2
log x 15 log x 4 0
log (7 x) log x 1 log 3
2
2
2
2
2
2




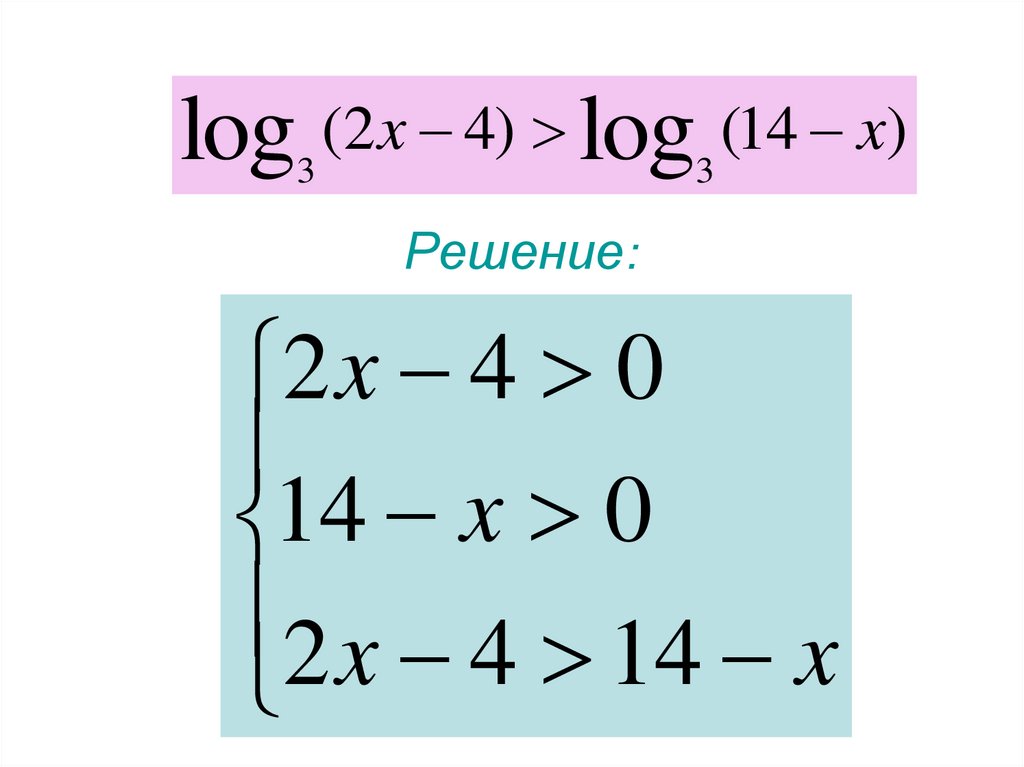

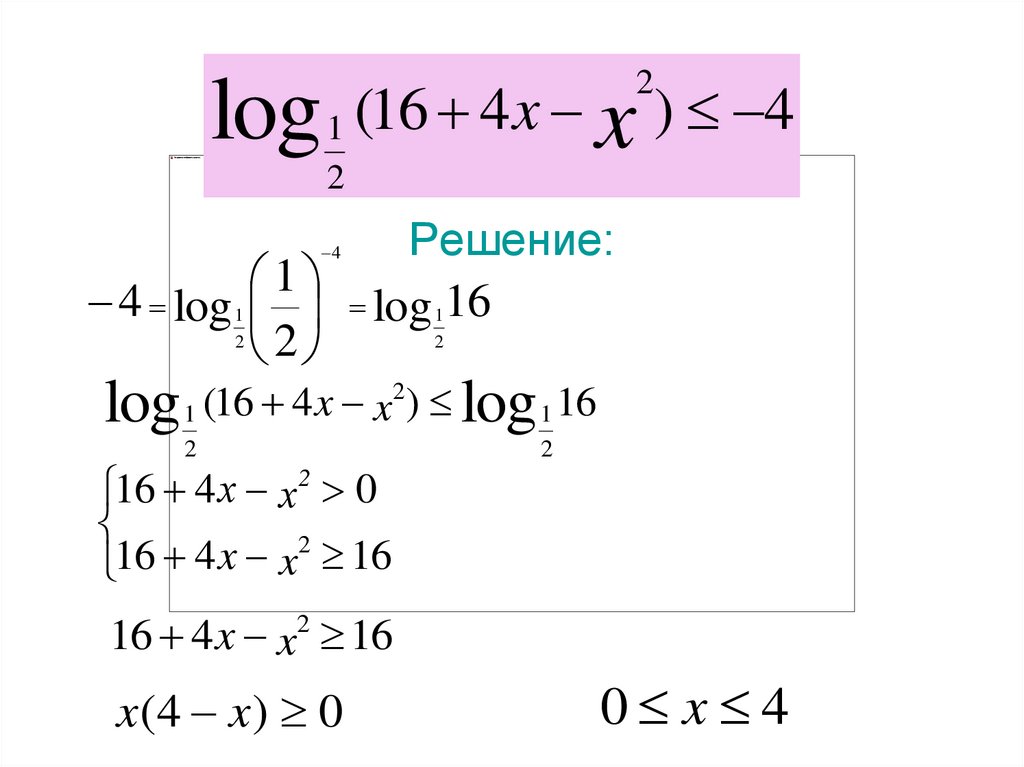





 Математика
Математика








