Похожие презентации:
Engineering Mechanics Part II: Dynamics . Lectures 7 - 9
1. Engineering Mechanics Part II: Dynamics Dr. Bahaa Saleh
2. Course Topics
• Chapter 1: Introduction to dynamics• Chapter 2: Kinematics of a Particle:
Topic # 1: Particle motion along a straight line
Topic # 2: Particle motion along a curved path
Topic # 3: Dependent motion of connected particles
Topic # 4: Relative motion of two particles
• Chapter 3: Kinetics of a Particle:
Topic # 1: Force and Acceleration
Topic # 2: Work and energy
Topic # 3: Impulse and momentum
3. Course Topics – Cont.
• Chapter 4: Planer Kinematics of a RigidBody.
• Chapter 5: Planar Kinetics of a Rigid
Body: Force and Acceleration.
• Chapter 6: Introduction to Mechanical
Vibration.
3
م04:13 24/06/2020
4. Chapter 3: Kinetics of a Particle Topic # 1: Force and Acceleration
5. First Law
• Law of inertia - a body in motion will stay inmotion and a body at rest will stay at rest
unless acted upon by a net external force.
• A particle originally at rest, or moving in a
straight line with a constant velocity, will
remain in this state provided the particle is
not subjected to an unbalanced force.
• Static law
6. Second Law
• A particle acted upon by an unbalanced forceF experiences an acceleration that has the
same direction as the force and a magnitude
that is directly proportional to the force
F a
F ma
a2
F2
a3
F3
7. Third Law
• Law of Action-Reaction - For everyaction, there is an equal and opposite
reaction.
• The mutual forces of
action and reaction
between two particles
are equal, opposite,
and collinear.
F12 F21
8. Summary of Newton’s laws
1- Law of inertia a body in motion will stay in motion and a body atrest will stay at rest unless acted upon by a net external force.
2- Law of force-acceleration A particle acted upon by an unbalanced
force F experiences an acceleration a that has the same direction
as the force and a magnitude that is directly proportional to the
force
F ma
3- Law of action-reaction for every action, there is an equal and
opposite reaction
mg = FN
9. The Equation of Motion Free Body and Kinetic Diagram
When more than one force acts on a particle, the resultant force isdetermined by a vector summation of all the forces. The equation
of motion may be written as
FR F m a
• Free-Body diagram (Force Diagram)
• Kinetic diagram (acceleration Diagram)
10. Equations of Motion: Rectangular Coordinates
• When the net force isprojected to separate
coordinate axes the
Newton’s second law
still holds
F ma
F
F
F
x
max
y
ma y
z
maz
11.
Free Body Diagram Method•Draw each object separately
•Draw all the forces acting on that object
•Get x and y components of all the forces to
calculate the net force
•Apply Newton’s second law to get acceleration
•Use the acceleration in any motion analysis and
establish a Kinetic Diagram
ma
12. Normal & Frictional Force
Normal & Frictional Forcemg = FN
F
mg
Ff
FN
13.
Static Friction ( ms )• Static friction – parallel force on the
surface when there is no relative
motion between the 2 objects
• Static friction force can vary from
zero to Maximum
Static Dynamic
Ff = msFN Ff = mkFN
F f μ s FN
Friction
The coefficient of static friction
is material dependent.
Applied external force
14.
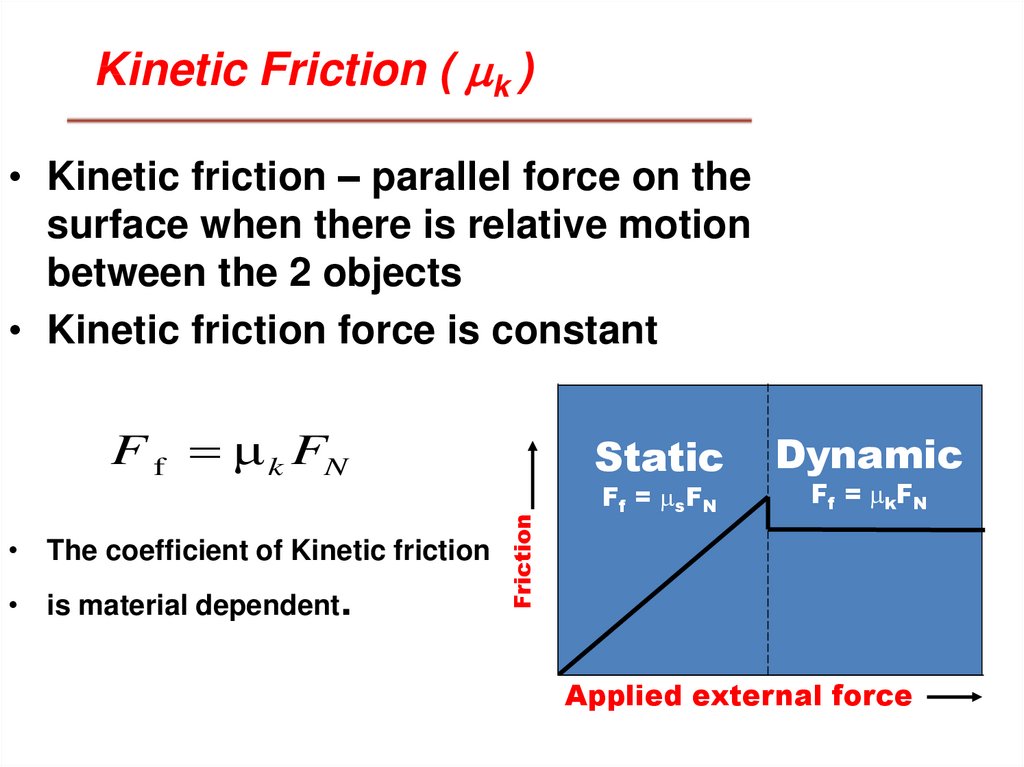
Kinetic Friction ( mk )• Kinetic friction – parallel force on the
surface when there is relative motion
between the 2 objects
• Kinetic friction force is constant
F f μ k FN
• is material dependent.
Friction
• The coefficient of Kinetic friction
Static
Ff = msFN
Dynamic
Ff = mkFN
Applied external force
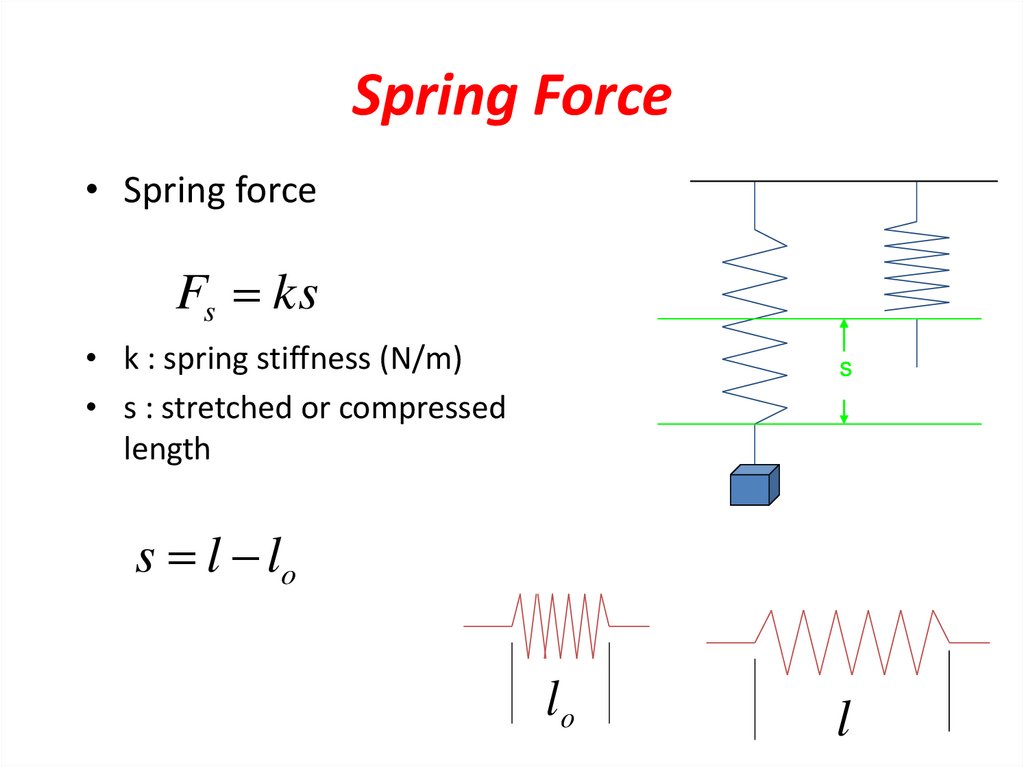
15. Spring Force
• Spring forceFs ks
• k : spring stiffness (N/m)
• s : stretched or compressed
length
s
s l lo
lo
lo
ll
16.
Problemmg
y
ma
x
N
mk N
a=?
N mg cos 0
F
y
0;
Fx max
N 40 9.81 cos 20 0
N 369 N
mk N mg sin ma
0.25(369) 40 9.81 sin 20 40ax
ax 5.66 m / s 2
17.
04:13 24/06/2020م17
18. Chapter 3: Kinetics of a Particle Topic # 2: Work and Energy
19.
Work of external Force W1 2• A force does work when it moves
through a
displacement in the direction of the force.
•Work is positive when the force component is in the
same direction as its displacement, otherwise it is
negative
• Forces that are functions of displacement must be
integrated to obtain the work. Graphically, the work is
equal to the area under the force-displacement curve.
20.
Work of external Force W1 2Work = Force F, (N) * displacement S, (m) = Joule
F
1
2
F cos θ
S
W1 2 S * F cos
21.
Work of a Weight• The work of a weight is the product of the
weight magnitude (W) and the vertical height
from reference plane (y).
UW W y
• The work is positive when the weight moves
downwards (the reference plane under the body).
• The work is negative when the weight moves
upwards (the reference plane over the body).
• The work is zero when the reference plane
pass with the body).
22.
Work of a WeightUU1 12 2 W ( yy) )
magnitude of the particle' s weight times
its vertical displaceme nt.
magnitude of the particle' s weight times
its vertical displacement.
23.
Work of a Spring ForceThe work of a spring is of the form
US
1
2
ks
2
where k is the spring stiffness (N/m)
S is the stretch or compression of the spring, m
24.
Work of a Spring ForceA mistake in sign can be avoided when applying this equation
if one simply notes the direction of the spring force acting on
the particle and compares it with the sense of direction of
displacement of the particle if both are in the same sense,
positive work results; if they are opposite to one another, the
work is negative.
11 2 2 1 1 2 2
UU
(( ks
ks2 2 ksks
) )
1 1
1 2s
22
22
1
2
U s k s
2
25.
The kinetic energyThe kinetic energy (T), Joule at the initial and final
points is always positive, since it involves the speed
squared
1
2
T mV
2
Where m is the particle mass, kg
V is the particle speed in m/s
26.
Principle of Work and EnergyW1 2 T2 T1
whereW1 2 is the external force work
T1and T2 are the initial and final kinetic energy
27.
Principle of Work and EnergyW1 2 T1 U1 T2 U 2
whereW1 2 is the external force work
T1and T2 are the initial and final kinetic energy
U UW U S
UW is the weigth work
U S is the spring work
28.
04:13 24/06/2020م28
29.
04:13 24/06/2020م29
30. Chapter 3: Kinetics of a Particle Topic # 3: Impulse and Momentum
31.
Principle of Linear Impulse and MomentumF ma m dv
dt will integrate the equation of
In this section we
t2
v2
t1
v1
Fdt respect
m dv
motion
to time and thereby obtain
with
the principle of impulse and momentum.
The resulting equation will be useful for solving
problems involving force, velocity, and time.
Principle of linear impulse and momentum equation
32. Newton’s Second Law
dvF madv m dt
t2
v2 dt
t1
v1
Fdt m d v
t2
Fdt mv
2
m v1
t1
Impulse
change in momentum
This equation is referred to as the principle of linear impulse and
momentum
33. Principle of Linear Impulse and Momentum
t2Fdt mv
2
m v1
t1
For problem solving, pervious equation will be rewritten in the
form
tt22
mv
v11
Fdt m v 2
m
tt11
• which states that the initial momentum of the particle
at time t1 plus the sum of all the impulses applied to
the particle from t1 to t2 is equivalent to the final
momentum of the particle at time t2.
34. Principle of Linear Impulse and Momentum
tt22m
Fdt
dt
m
mvv22
mv 1 F
tt11
If each of the vectors in above Eq. is resolved into its x, y, z
components, we can write the following three scalar equations
of linear impulse and momentum.
t2
m (v x )1 Fx dt m (v x ) 2
t1
t2
m (v y )1 Fy dt m (v y ) 2
t1
t2
m (v z )1 Fz dt m (v z ) 2
t1
35.
The 100-kg stone shown in Fig. is originally at rest on the smooth horizontal surface. Ifa towing force of 200 N, acting at an angle of 45°, is applied to the stone for 10 s,
determine the final velocity and the normal force which the surface exerts on the stone
during this time interval.
m=100 kg
t2
( ) m( x )1 Fx dt m( x ) 2
t1
0 200 N cos 45o (10s) (100 kg) 2
2 14.1 m / s
m(
t2
) Fy dt m( y ) 2
y 1
t1
0 N c (10s) 981N (10s) 200 N (10s) sin 45o 0
N c 840 N
At rest smooth
t=10 s
V2=?
N=?
36.
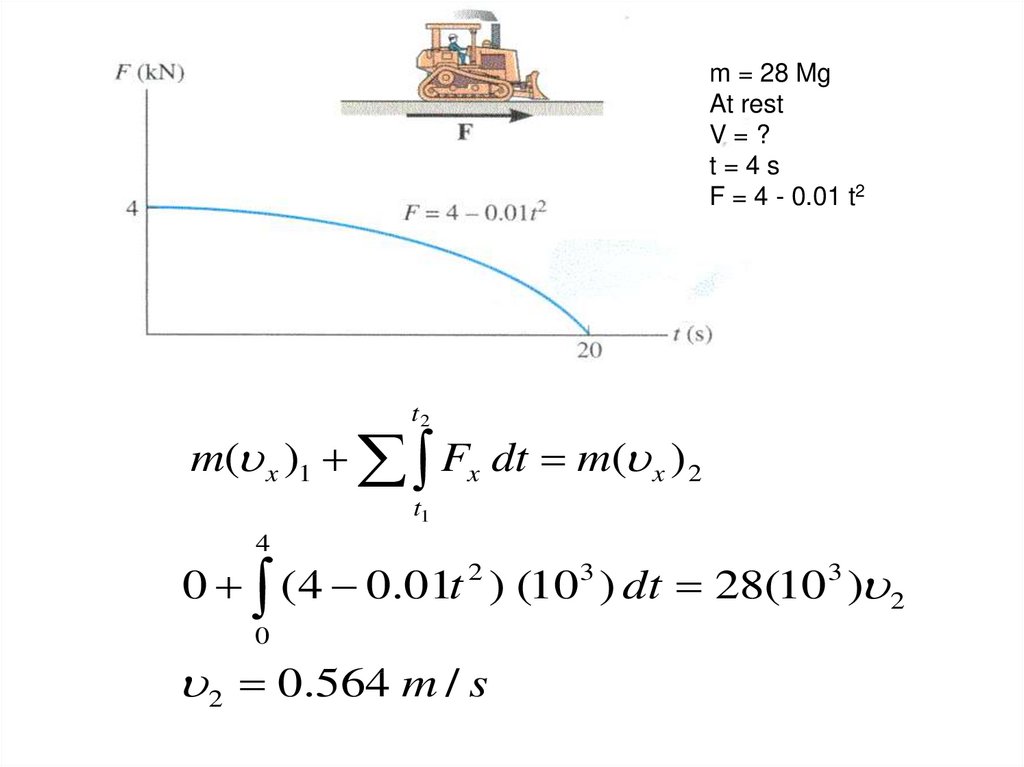
m = 28 MgAt rest
V=?
t=4s
F = 4 - 0.01 t2
t2
m( x )1 Fx dt m( x ) 2
t1
4
0 ( 4 0.01t ) (10 ) dt 28(10 ) 2
2
0
2 0.564 m / s
3
3
37.
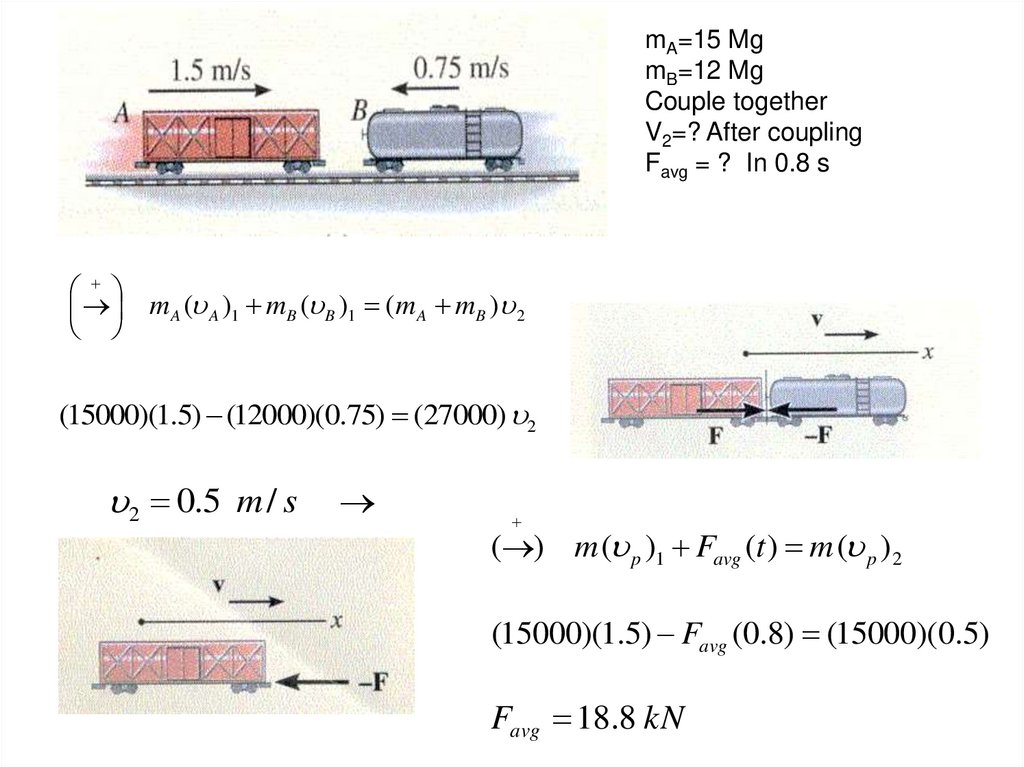
The 15-Mg boxcar A is coasting at 1 .5 mls on the horizontal trackwhen it encounters a 12-Mg tank car B coasting at 0.75 mls
toward it as shown in Fig. 15-Sa. If the cars collide and couple
together, determine (a) the speed of both cars just after the
coupling, and (b) the average force between them if the coupling
takes place in O.S s.
m A ( A )1 mB ( B )1 (m A mB ) 2
(15000)(1.5) (12000)(0.75) (27000) 2
2 0.5 m / s
mA=15 Mg
mB=12 Mg
Couple together
V2=? After coupling
Favg = ? In 0.8 s
( ) m ( p )1 Favg (t ) m ( p ) 2
(15000)(1.5) Favg (0.8) (15000)(0.5)
Favg 18.8 kN
38.
mA=15 MgmB=12 Mg
Couple together
V2=? After coupling
Favg = ? In 0.8 s
m A ( A )1 mB ( B )1 (m A mB ) 2
(15000)(1.5) (12000)(0.75) (27000) 2
2 0.5 m / s
( ) m ( p )1 Favg (t ) m ( p ) 2
(15000)(1.5) Favg (0.8) (15000)(0.5)
Favg 18.8 kN
39.
04:13 24/06/2020م39

































 Физика
Физика








