Похожие презентации:
Engineering Mechanics Part II: Dynamics. Lectures 1 - 3
1. Engineering Mechanics Part II: Dynamics Dr. Bahaa Saleh
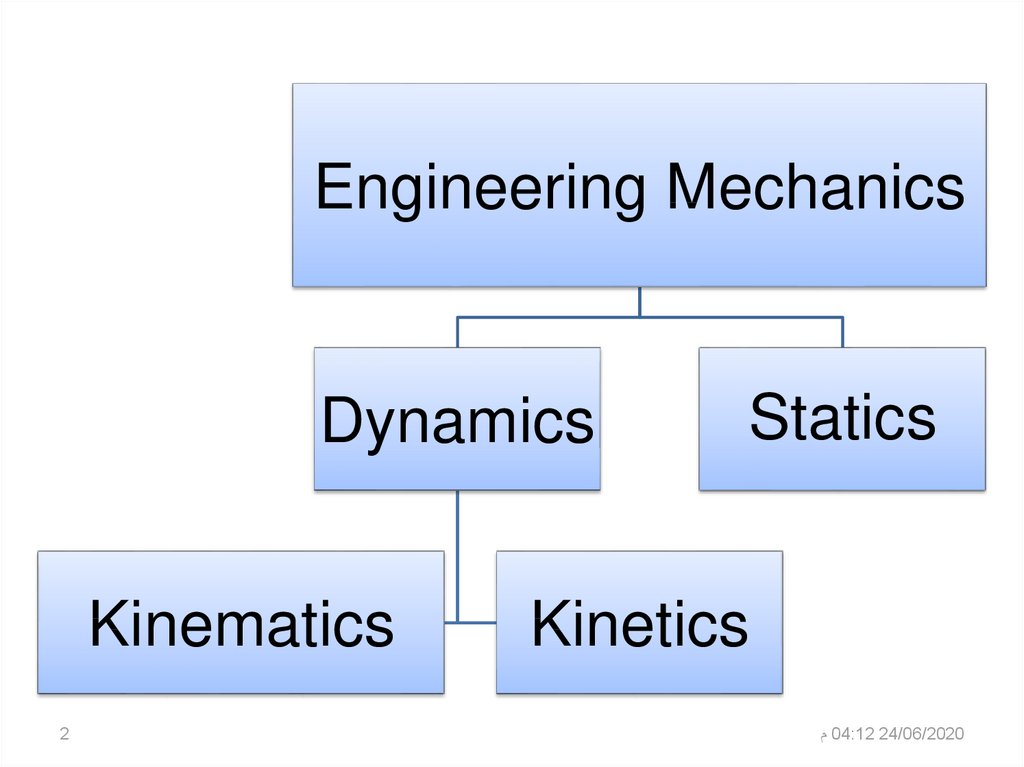
2.
Engineering MechanicsDynamics
Kinematics
2
Statics
Kinetics
م04:12 24/06/2020
3.
Course Supplemental MaterialsTextbook - Engineering Mechanics:
Dynamics, R. C. Hibbeler, 8th Edition,
Pearson Prentice Hall, 1998.
References: Engineering Mechanics:
Dynamics , J . L. Meriam and L. G. Kraige ,
6th Edition, John Wiley & Sons, Inc., 2008.
Lectures Notes prepared by instructors.
4. Course Grading System
• 20%• 20%
• 20%
• 40%
Attendance, participation,
Quizzes and assignments
1st Midterm Exam
2nd Midterm Exam
Final Exam
5. Course Topics
• Chapter 1: Introduction to dynamics• Chapter 2: Kinematics of a Particle:
Topic # 1: Particle motion along a straight line
Topic # 2: Particle motion along a curved path
Topic # 3: Dependent motion of connected particles
Topic # 4: Relative motion of two particles
• Chapter 3: Kinetics of a Particle:
Topic # 1: Force and Acceleration
Topic # 2: Work and energy
Topic # 3: Impulse and momentum
6. Course Topics – Cont.
• Chapter 4: Planer Kinematics of a RigidBody.
• Chapter 5: Planar Kinetics of a Rigid
Body: Force and Acceleration.
• Chapter 6: Introduction to Mechanical
Vibration.
6
م04:12 24/06/2020
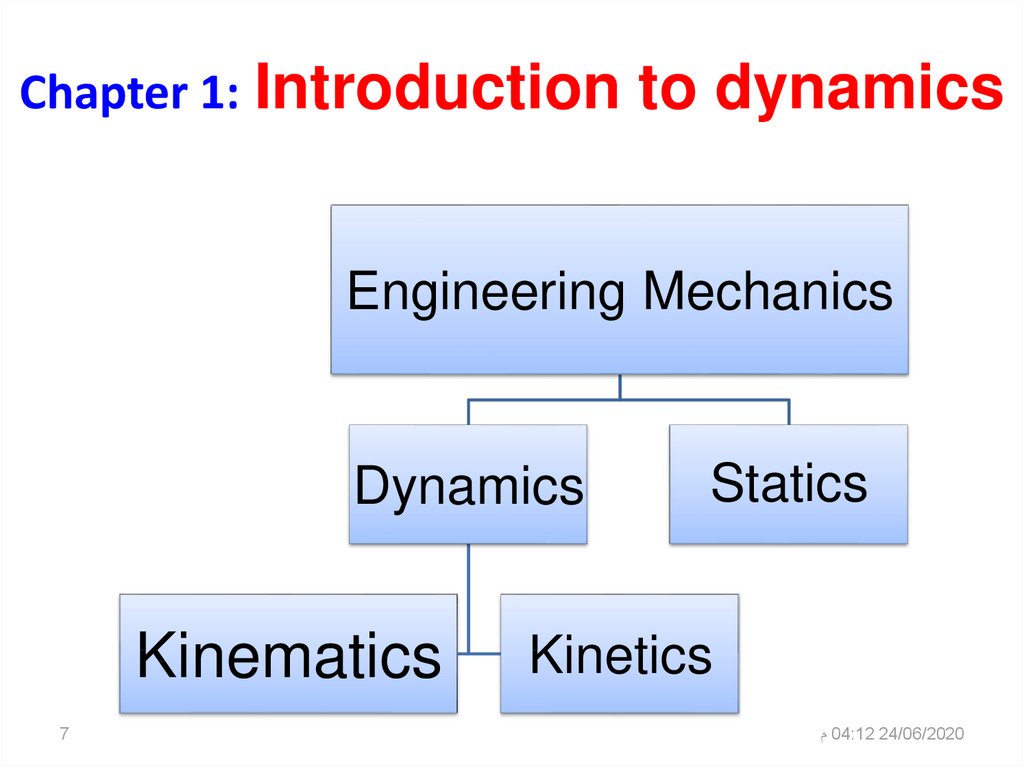
7. Chapter 1: Introduction to dynamics
Engineering MechanicsDynamics
Kinematics
7
Statics
Kinetics
م04:12 24/06/2020
8. Definitions
• Statics: concerned with theequilibrium of a body that is
either at rest or moves with
constant velocity.
8
م04:12 24/06/2020
9. Definitions – Cont.
Dynamics1- Kinematics: study of the motion of
particles/rigid
bodies
(relate
displacement, velocity, acceleration,
and time, without reference to the
cause of the motion).
• 2- Kinetics: study of the forces acting
on the particles/rigid bodies and the
motions resulting from these forces.
9
م04:12 24/06/2020
10. Definitions – Cont.
• Rigid Body• Particle
10
م04:12 24/06/2020
11. Review of Vectors and Scalars
• A Scalar quantity has magnitude only.• A Vector quantity has both magnitude and
direction.
12.
• Scalars (e.g)– Distance
– Mass
– Temperature
– Pure numbers
– Time
– Pressure
– Area
– Volume
• Vectors (e.g.)
– Displacement
– Velocity
– Acceleration
– Force
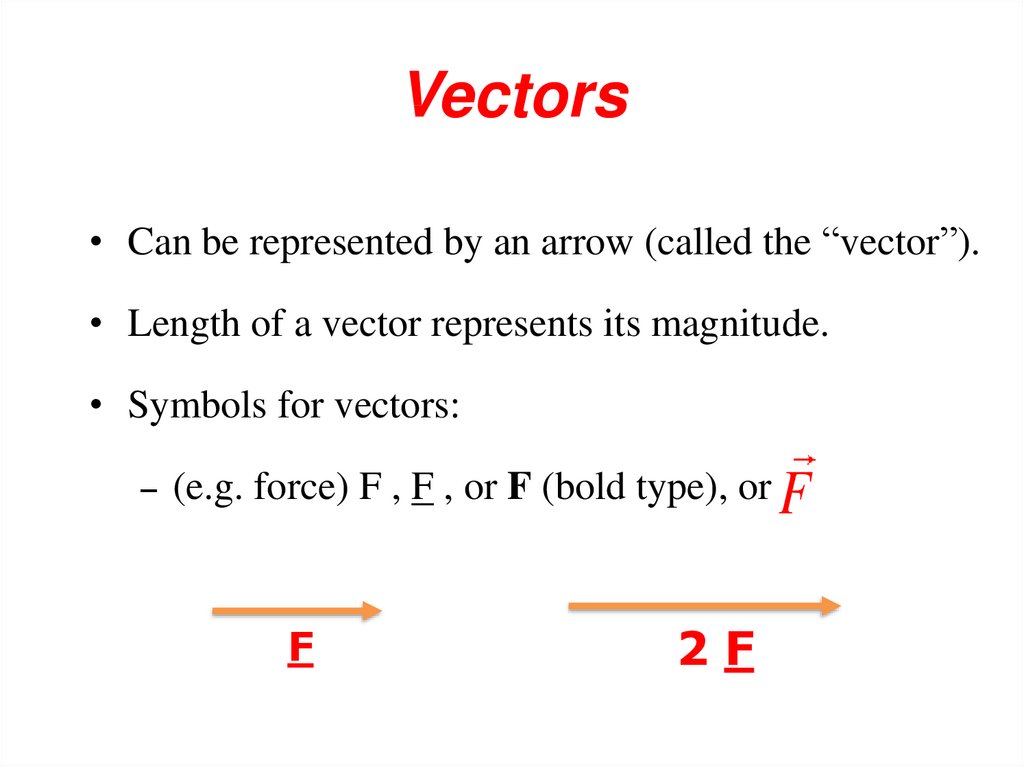
13. Vectors
• Can be represented by an arrow (called the “vector”).• Length of a vector represents its magnitude.
• Symbols for vectors:
–
(e.g. force) F , F , or F (bold type), or F
F
2F
14. Chapter 2: Kinematics of a Particle: Topic # 1: Particle motion along a straight line (Rectilinear Motion)
15. Definition
Rectilinear motion: A particle movingalong a horizontal/vertical/inclined straight
line.
16. Position of the particle (horizontal)
• Since the particle is moving, so theposition is changing with time (t):
• OP = Position = S = S (t)
17. Displacement of the particle (horizontal)
• Displacement (∆s) : The displacementof the particle is the change in its
position.
18. Displacement of the particle (horizontal)
1- ∆S is positive since the particle's finalposition is to the right of its initial position,
i.e., s` > s.
2- If the final position to the left of its initial
position, ∆S would be negative.
19. Velocity of the particle (horizontal)
• Velocity (v) : If the particle displacement ∆s duringtime interval ∆t, the average velocity of the
particle during this time interval is (displacement
per unit time)
• The magnitude of the velocity is known as the
speed, and it is generally expressed in units of m/s
v av
s
t
20. Velocity of the particle (horizontal)
• Instantaneous velocity :s
V lim
t 0 t
ds
v
dt
• So (v) is a function of time (t):
v v(t)
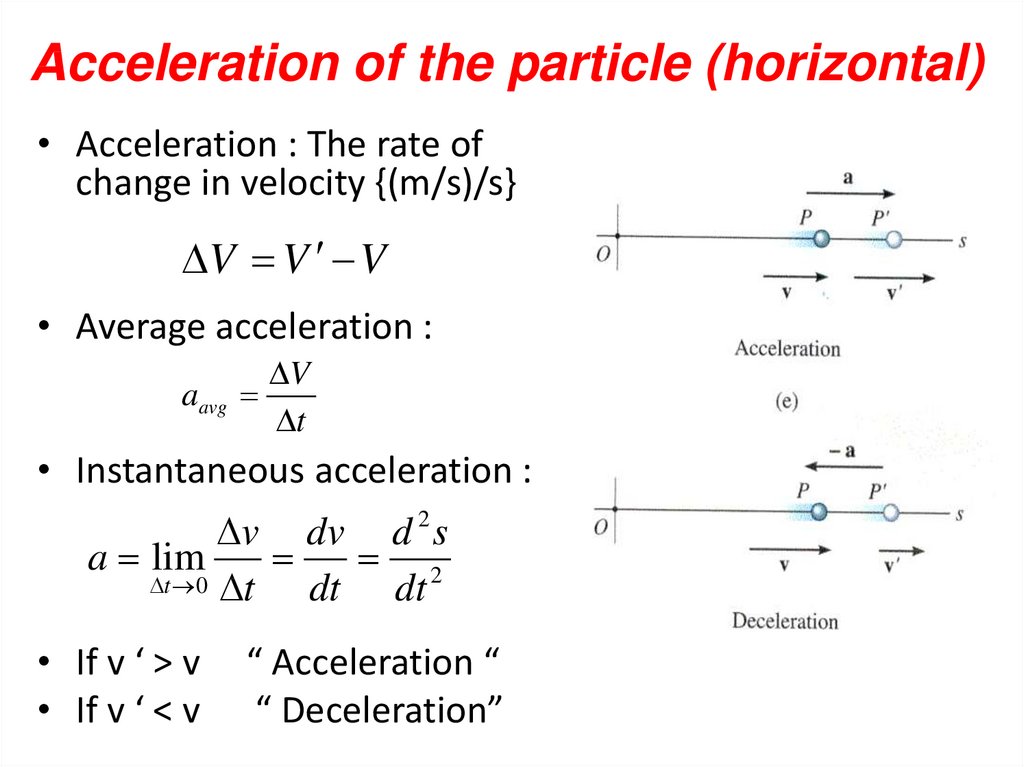
21. Acceleration of the particle (horizontal)
• Acceleration : The rate ofchange in velocity {(m/s)/s}
V V V
• Average acceleration :
aavg
V
t
• Instantaneous acceleration :
v dv d 2 s
a lim
2
t 0 t
dt dt
• If v ‘ > v
• If v ‘ < v
“ Acceleration “
“ Deceleration”
22. Acceleration of the particle (horizontal)
• Acceleration (a) : is the rate of change ofvelocity with respect to time.
2
dv d s
a
2
dt dt
23. Solved Examples
Example 1• A particle moves along a straight line such that its
position is defined by s = (t3 – 3 t2 + 2 ) m.
Determine the velocity of the particle when t = 4 s.
ds
2
v
3t 6t
dt
At t = 4 s,
the velocity (v) = 3 (4)(4) – 6(4) = 24 m/s
24.
Example 2• A particle moves along a straight line such that its
position is defined by s = (t3 – 3 t2 + 2 ) m.
Determine the acceleration of the particle when
t = 4 s.
ds
v
3t 2 6t
dt
dv
a
6t 6
dt
• At t = 4
a(4) = 6(4) - 6 = 18 m/s2
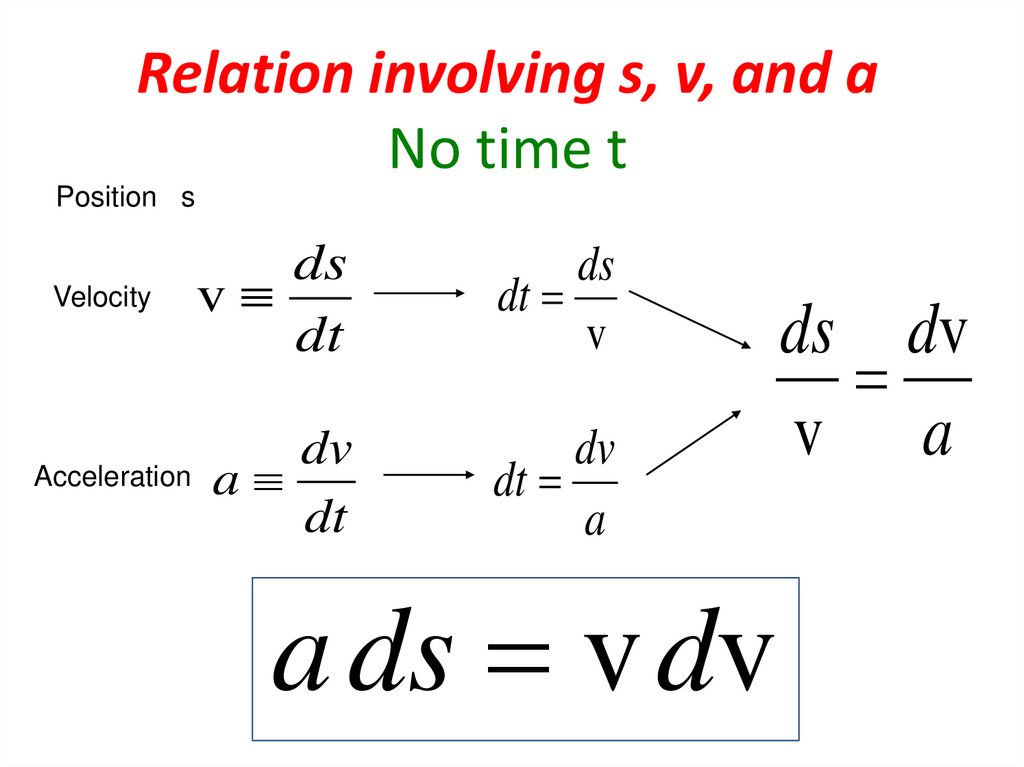
25. Relation involving s, v, and a No time t
Position sVelocity
Acceleration
ds
v
dt
ds
dt
v
dv
a
dt
dv
dt
a
a ds v dv
ds dv
v a
26. Motion with uniform/constant acceleration a
dva
dt
v
t
vo
0
dv
a
dt
dv a dt
v v 0 at
v v 0 at
27. Motion with uniform/constant acceleration a
dsv
v0 a t
dt
s
t
so
0
ds
(
v
a
t
)
dt
0
1 2
s s0 v 0 t a t
2
28. Motion with uniform/constant acceleration a
v dv a dsv
s
v0
s0
v
d
v
a
ds
1 2 1 2
v v 0 ac ( s s 0 )
2
2
v v 2 a ( s s0 )
2
2
0
29. Summary
• Time dependent acceleration• Constant acceleration
s s (t )
v v0 a t
ds
v
dt
2
dv d s
a
2
dt dt
a ds v dv
1 2
s s0 v 0 t a t
2
v v 2 a ( s s0 )
2
2
0
30.
Example 3• A car moves in a straight line such that for a short time its
velocity is defined by v = (3t^2 + 2t) m/s, where t is in
seconds. Determine its position and acceleration when t =
3 s. (When t = 0, s = o).
When t = 3 s
s 3 3 36 m
3
2
a 6 * 3 2 20 m s
2
31. Chapter 2: Kinematics of a Particle: Topic # 2: Particle Motion along a Curved Path
32.
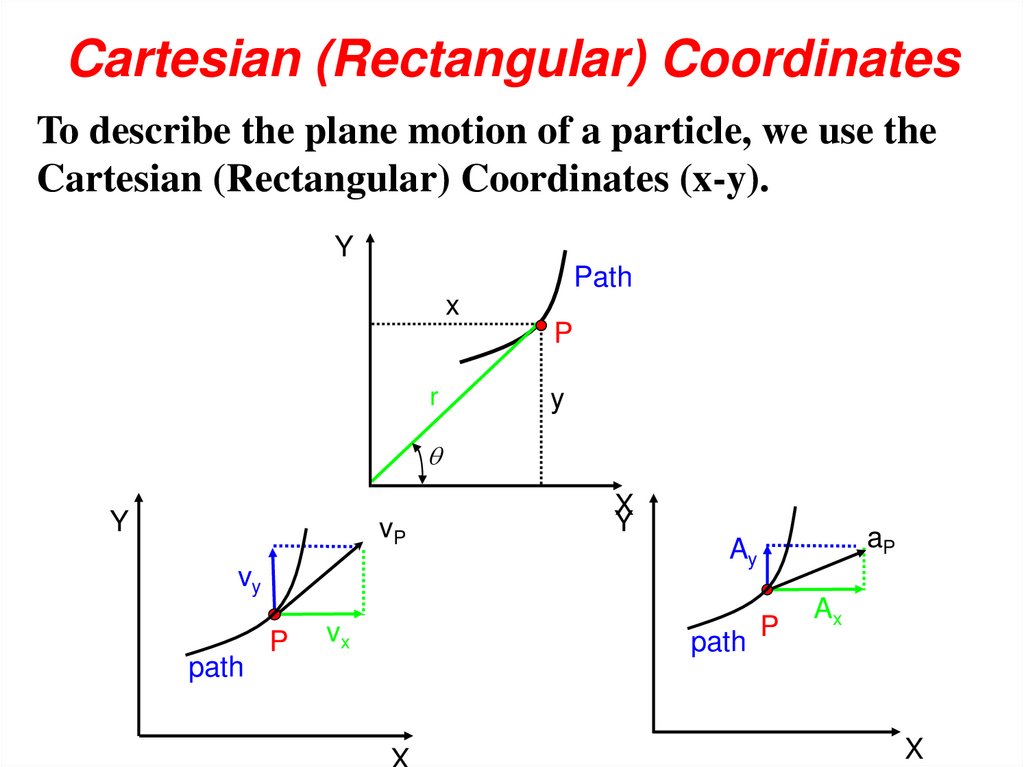
Cartesian (Rectangular) CoordinatesTo describe the plane motion of a particle, we use the
Cartesian (Rectangular) Coordinates (x-y).
Y
Path
x
P
r
y
Y
vP
vy
path
P
vx
X
Y
path
X
aP
Ay
P
Ax
X
33. 12Projectile Motion
• Projectile: any body that is given an initialvelocity and then follows a path determined by
the effects of gravitational acceleration and air
resistance.
• Trajectory – path followed by a projectile
34.
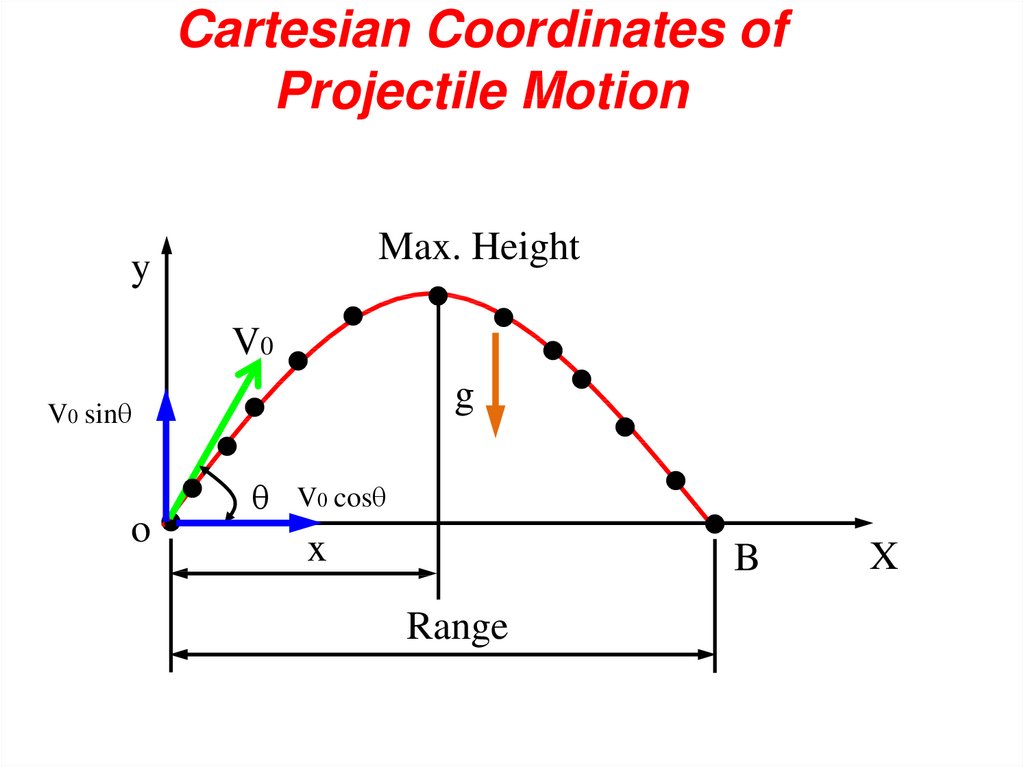
Cartesian Coordinates ofProjectile Motion
Max. Height
y
V0
g
V0 sin
o
V0 cos
x
B
Range
X
35.
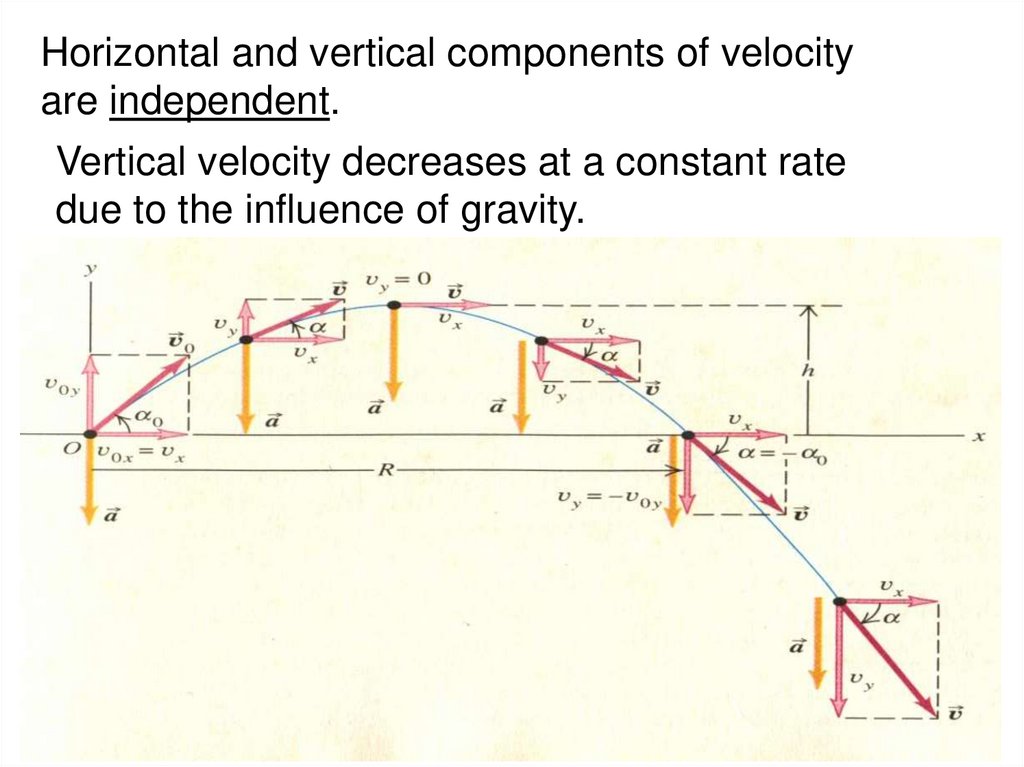
Horizontal and vertical components of velocityare independent.
Vertical velocity decreases at a constant rate
due to the influence of gravity.
36.
Cartesian Coordinates ofProjectile Motion
• Assumptions:
(1) free-fall acceleration
(2) neglect air resistance
• Choosing the y direction as positive upward:
ax = 0;
ay = - g (a constant)
y
v0
• Take x0= y0 = 0 at t = 0
• Initial velocity v0 makes an
x
angle with the horizontal
v 0x v 0 cosθ
v 0y v 0sin θ
37. Horizontal Motion of Projectile
• Acceleration in X-direction: ax= 0• Integrate the acceleration yields:
( ) v x v 0 cosθ constant
• Integrate the velocity yields:
( ) x v 0 t cosθ
38. Vertical Motion of Projectile
• ay = ac= -g = -9.81 m/s2• Integrate the acceleration yields:
( ) v v0 ac t
( )
v y (v0 ) y gt
v y v 0 sinθ gt
• Integrate the velocity yields:
( )
gt 2
y v 0 t sinθ
2
39.
• ax = 0;ay = - g (a constant)
• Integration of these acceleration yields
v x v0 cosθ constant
v y v 0 sin θ g t
x v 0 t cosθ
(1)
y v 0 t sin θ g t /2
2
(2)
• Elimination of time t from Eqs. 1 & 2 yields
• Equation of the path of projectile
y x tan θ (g x sec θ / 2 v )
2
2
2
o
(3)
40.
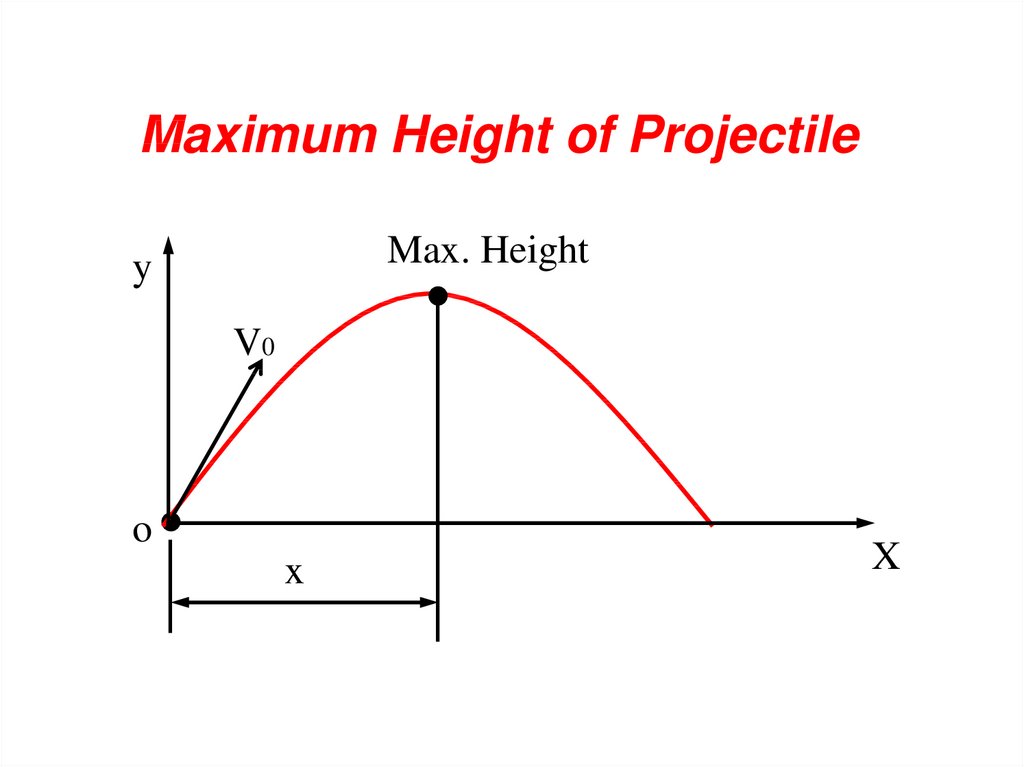
Maximum Height of ProjectileMax. Height
y
V0
o
x
X
41.
Maximum Height of ProjectileAt the peak of its trajectory, vy = 0.
v y v 0y a t v o sin gt 0
v 0 sin
Time t1 to reach the peak t1
g
g
1 2
Substituting into: y v 0 sin t gt
2
v 0y
h y max
v 0sinθ 1 v 0 sinθ
g
v 0sinθ
g 2 g
v 0sinθ
2
h y max
g
1 v 0sinθ
2
g
2
2
42.
Maximum Height of Projectilev 0 sin
1 v 0 sin
2
g
2
h y max
h y max
2
g
(v o sin )
v sin v
2g
2g
2g
2
2
o
2
2
0y
v 0 sinθ
v 0 sinθ
x v 0x t v 0x
v 0 cosθ
g
g
2
v o sin 2θ
sin2θ
x
sinθ cosθ
2g
2
43.
Maximum Height of Projectile andthe corresponding time and X
h y max
v sin
2g
2
o
2
o
v sin 2θ
x
2g
v 0 sin
t1
g
2
44.
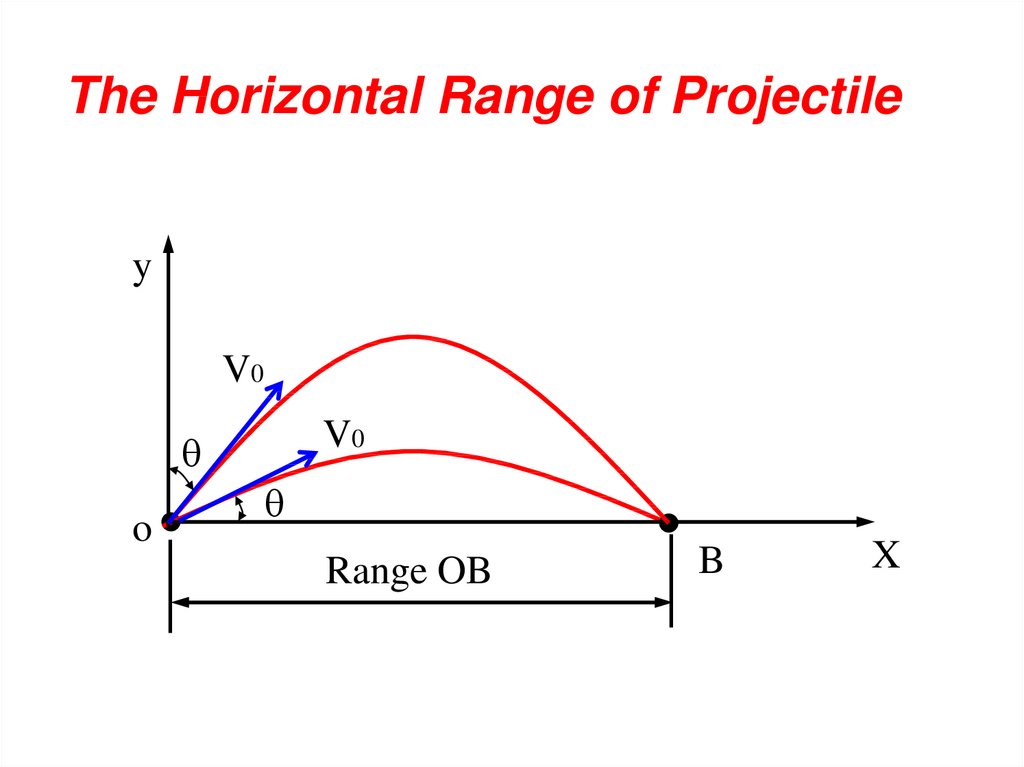
The Horizontal Range of Projectiley
V0
V0
o
Range OB
B
X
45.
The Horizontal Range of ProjectileThe range (OB) where y = 0.
1 2
y v 0 sin t gt
2
Time for the range OB
2 v 0 sin
tB
g
For the rang OB substitute into:
x v 0 t B cosθ
2
o
2v o
v
X OB v o cosθ
sinθ
2 sinθ cosθ
g
g
2
2
vo
vo
X OB
sin2(90 - θ)
sin2 θ
g
g
46.
The Horizontal Range of ProjectileFrom the Rang equation it is clear that an
angle of firing with the horizontal gives the
same range OB as an angle of firing (90 - )
with the horizontal or as an angle of with
vertical.
47.
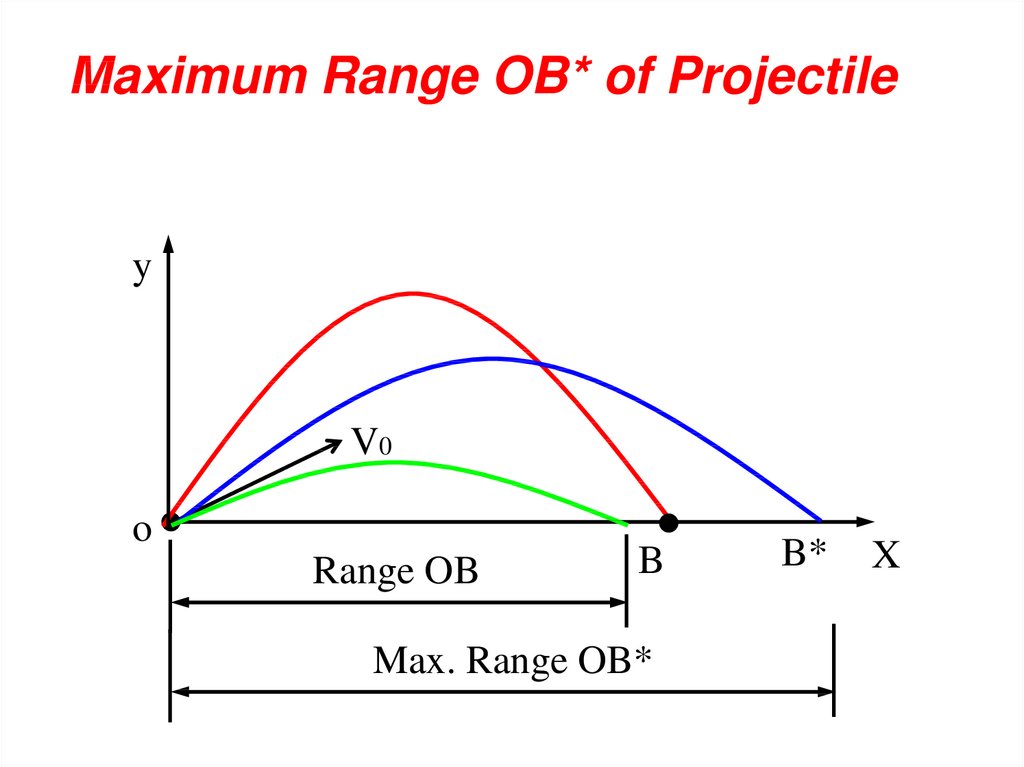
Maximum Range OB* of Projectiley
V0
o
Range OB
B
Max. Range OB*
B*
X
48.
Maximum Range OB* of ProjectileTo calculate max. Range (OB*) and its angle
2
o
v
X OB
sin2(90 - θ)
g
sin2(90 - θ) 1 sin(2 )
θ 45
2
vo
OB
g
*
o
49.
Projection Angle• The optimal angle of projection is dependent
on the goal of the activity.
• For maximal height the optimal angle is 90o.
• For maximal horizontal distance the optimal
angle is 45o.
50.
Projection angle = 10 degrees10 degrees
51.
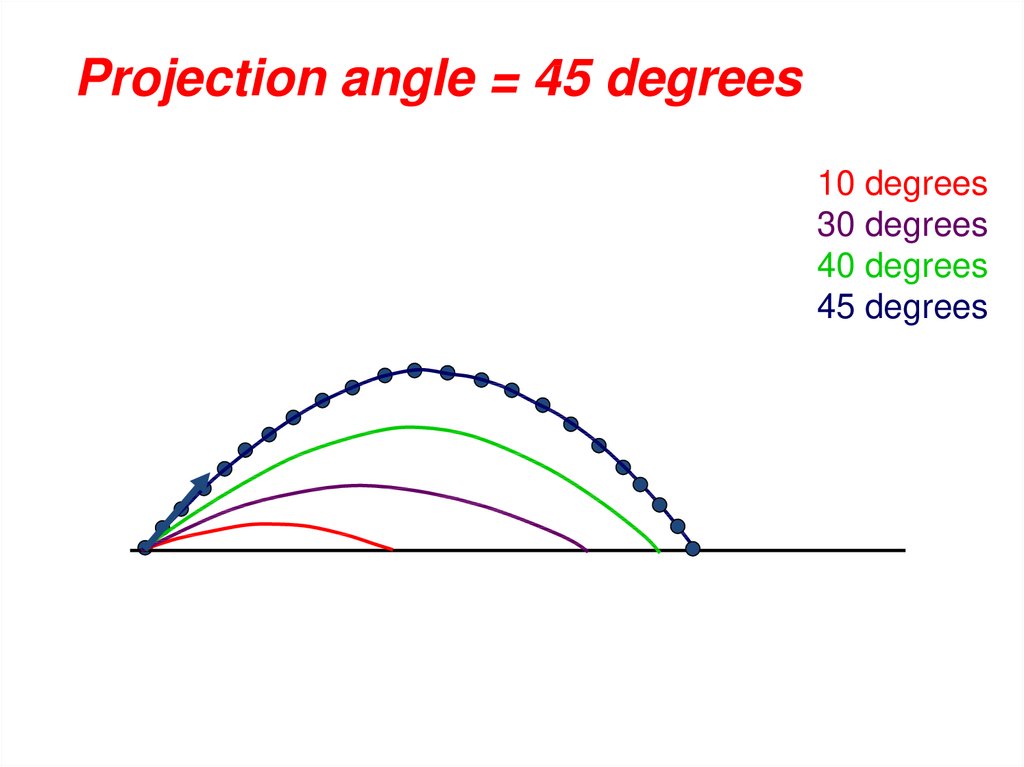
Projection angle = 45 degrees10 degrees
30 degrees
40 degrees
45 degrees
52.
Projection angle = 60 degrees10 degrees
30 degrees
40 degrees
45 degrees
60 degrees
80 degrees
53.
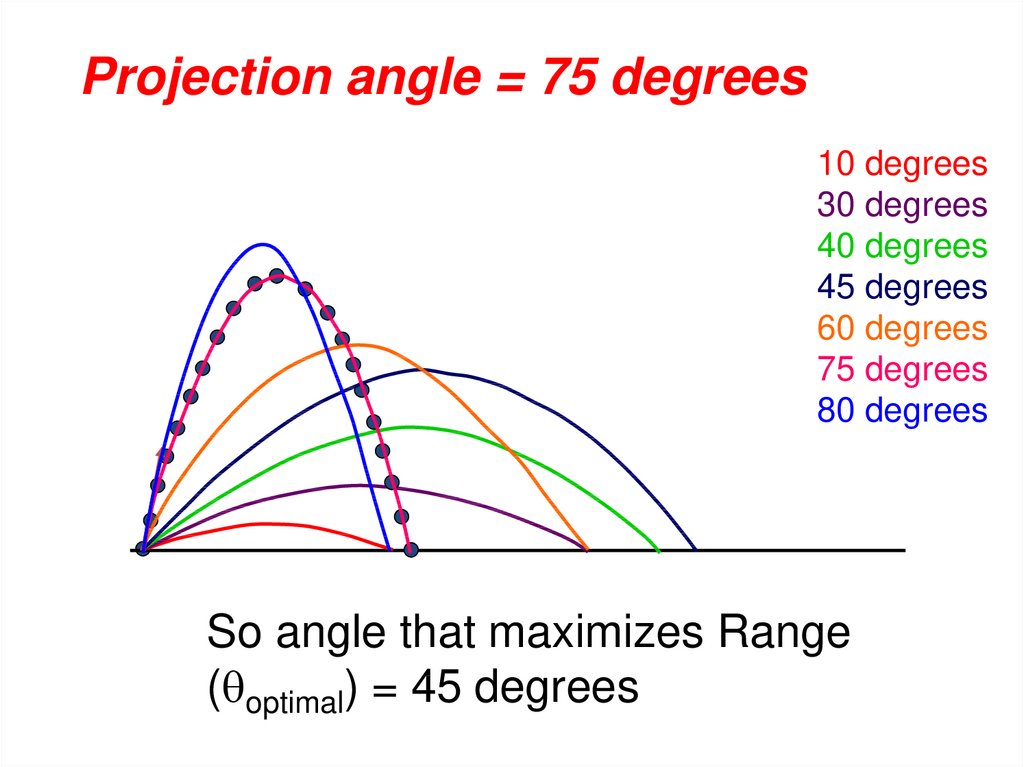
Projection angle = 75 degrees10 degrees
30 degrees
40 degrees
45 degrees
60 degrees
75 degrees
80 degrees
So angle that maximizes Range
( optimal) = 45 degrees
54.
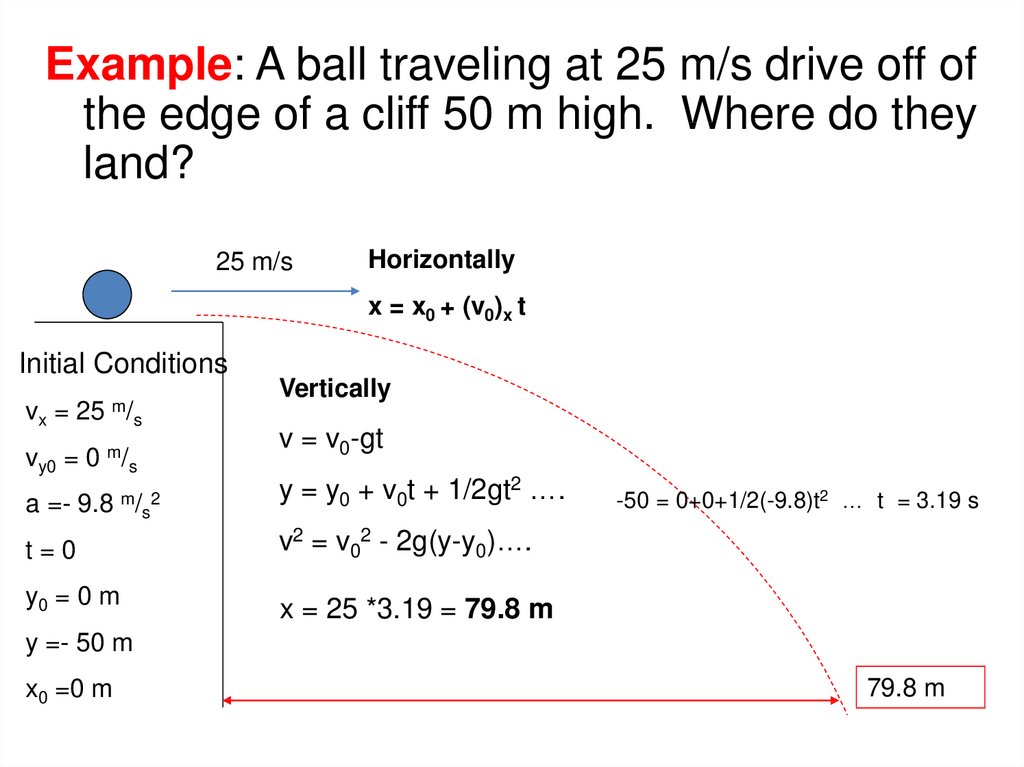
Example: A ball traveling at 25 m/s drive off ofthe edge of a cliff 50 m high. Where do they
land?
25 m/s
Horizontally
x = x0 + (v0)x t
Initial Conditions
vx = 25
m/
s
vy0 = 0 m/s
a =- 9.8
m/ 2
s
Vertically
v = v0-gt
y = y0 + v0t + 1/2gt2 ….
t=0
v2 = v02 - 2g(y-y0)….
y0 = 0 m
x = 25 *3.19 = 79.8 m
-50 = 0+0+1/2(-9.8)t2 … t = 3.19 s
y =- 50 m
x0 =0 m
79.8 m








































 Физика
Физика








