Похожие презентации:
Негармонические волны в равновесных средах с дисперсией. (Лекция 11)
1.
Лекция 11Негармонические волны в равновесных средах с дисперсией
1. Общее решение начальной задачи
а. Основные формулы для пространственно гармонических волн
б. Построение общего решения в случае негармонических волн
в. Пространственно временная функция точечного источника
г. Задача об эволюции негармонического начального возмущения
2. Квазигармоническое приближение. Групповая скорость
а. Спектральная плотность начального возмущения
б. Случай слабой дисперсии – групповая скорость
в. Скорость переноса энергии волны
г. Групповая скорость и метод медленных амплитуд
д. Групповые скорости конкретных волн
е. Поток энергии волн
3. Расплывание импульсов в равновесных средах с дисперсией
а. Постановка задачи и общие соображения
б. Компьютерное моделирование
в. Метод стационарной фазы
2.
A(t , z ) A(t , k ) exp(ikz )D( ˆ , k ) A(t , k ) F (t , k )
Pn 1 ( , k )
1
A(t , k )
exp( i t )d
2 C ( ) D( , k )
t
A(t , k ) G ( , k ) F (t , k )d
0
n
A(t , k ) Am (k ) exp i m (k )t
m 1
G (t , k )
1
1
exp( i t )d
2 C ( ) D ( , k )
D( ˆ , kˆ) A(t , z ) F (t , z )
1
A(t , z )
A(t , k ) exp(ikz )dk
2
A(t , k ) A(t , z ) exp( ikz )dz
Pn 1 ( , k )
1
A(t , z )
dk
exp( i t ikz )d
2
(2 ) C ( ) D( , k )
n
1
Am (k ) exp i m (k )t ikz dk
A(t , z )
2 m 1
A(t , z ) d dx G ( , x) F (t , z x)
0
t
D( ˆ , kˆ)G (t , z ) (t ) ( z )
1
1
1
G (t , z )
G
(
t
,
k
)
exp(
ikz
)
dk
dk
exp( i t ikz )d
2
(2 ) 2 C ( ) D( , k )
3.
1A(t , z )
A(k ) exp i (k )t ikz dk
2
1
A(k ) A0 ( z ) exp( ikz )dz A0 (k )
A(0, z )
A(k ) exp(ikz )dk A0 ( z )
z k ~ 2
2
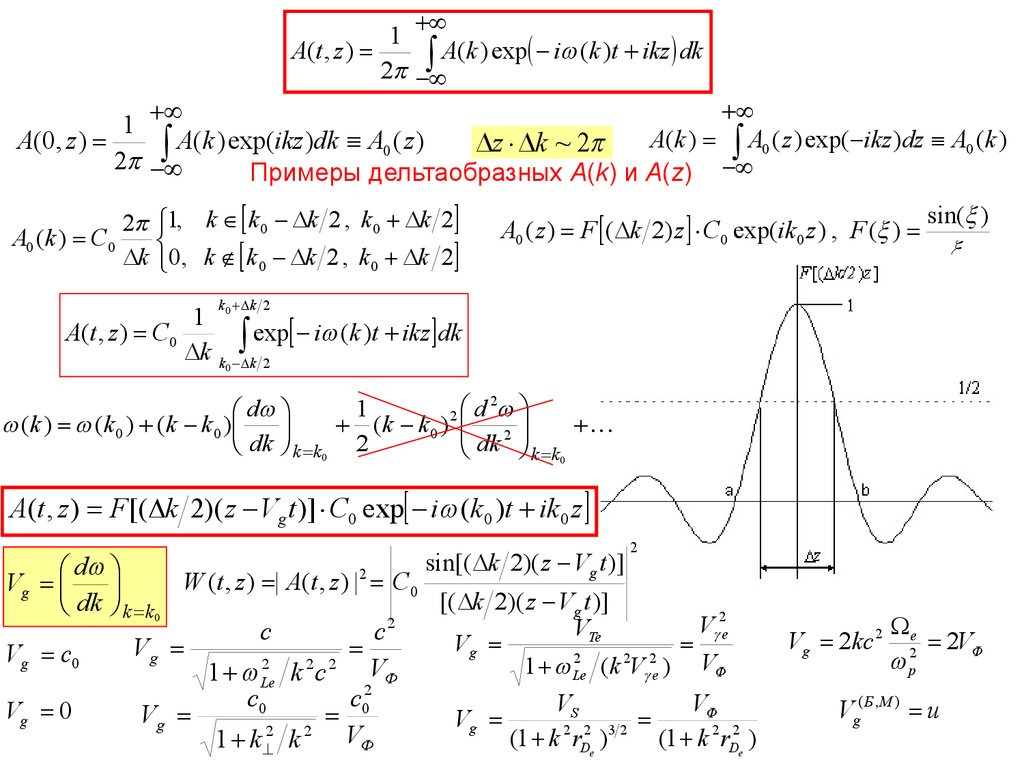
Примеры дельтаобразных A(k) и A(z)
2
A0 (k ) C0
k
1, k k 0 k 2 , k0 k 2
0, k k0 k 2 , k 0 k 2
1
A(t , z ) C0
k
A0 ( z ) F ( k 2) z C0 exp(ik0 z ) , F ( )
sin( )
k0 k 2
exp i (k )t ikz dk
k 0 k 2
2
1
d
2 d
(k ) ( k0 ) (k k0 )
(k k0 ) 2
dk k k0 2
dk k k0
A(t , z ) F [( k 2)( z Vg t )] C0 exp i (k0 )t ik0 z
sin[( k 2)( z Vg t )]
2
d
W (t , z ) | A(t , z ) |2 C0
Vg
[( k 2)( z Vg t )]
dk k k0
2
V 2e
VTe
c
c
Vg
Vg
Vg c0
2
2 2
2
2 2
1 Le (k V e ) VФ
VФ
1 Le k c
2
c
c
VS
VФ
0
0
Vg 0
Vg
V
g
(1 k 2 rD2 ) 3 2 (1 k 2 rD2 )
1 k 2 k 2 VФ
e
e
Vg 2kc 2
e
2VФ
p2
Vg( Б , М ) u
4.
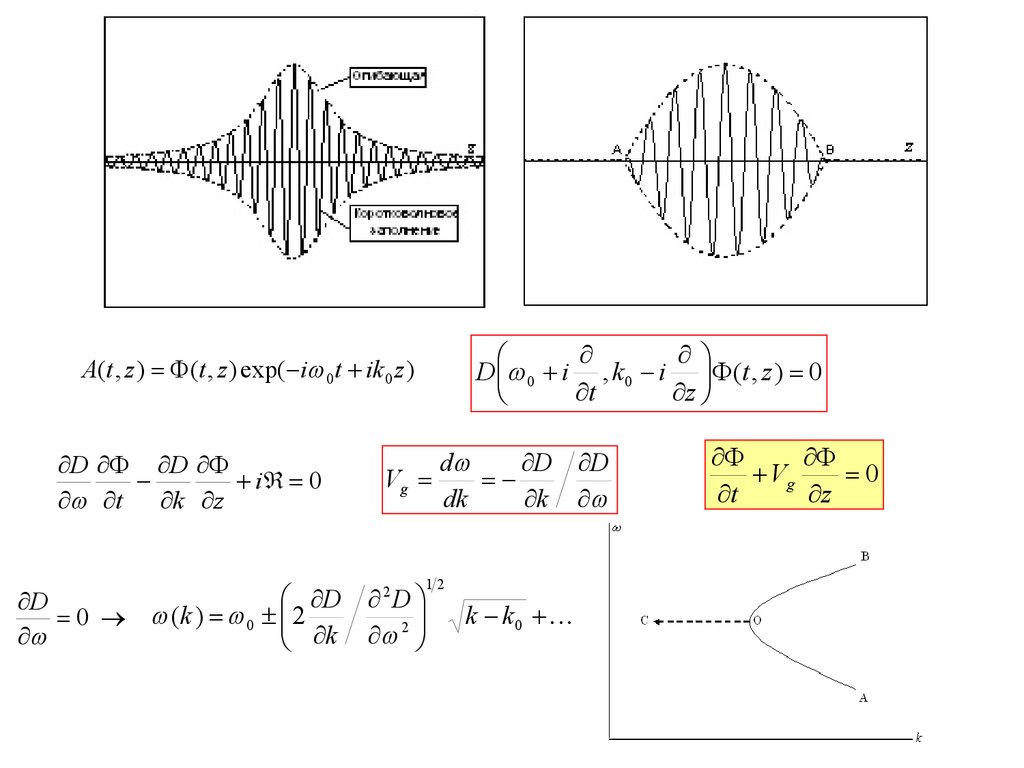
D 0 i , k 0 i (t , z ) 0t
z
A(t , z ) (t , z ) exp( i 0t ik 0 z )
D D
i 0
t k z
D
D
0 (k ) 0 2
k
d
D D
Vg
dk
k
12
2D
2
k k0
Vg
0
t
z
5.
~A(t , r ) A(t , r ) exp( i 0t ik 0r )
~
~
A
A
Vg
0
t
r
S(t , r ) VgW (t , r )
Vg
~
D 0 i , k 0 i A(t , r ) 0
t
r
d
D D
dk
k
W
W
Vg
0
t
r
W (t , r ) ~ | A(t , r ) |2
W
d
div S 0
W (t , r )dr S dσ
t
dt V
| E~l (t , r ) |2
l
S l (t , r ) [ ( , k )]
k
16
tr
k 2 c 2 | E~tr (t , r ) |2
S tr (t , r )
( , k ) 2
k
16
kc 2 | E~tr (t , r ) |2
S tr (t , r )
8
c[E B] 4
k 2 2 | E~l (t , r ) |2
S l (t , r ) V e 2
2
Le
8
l tr 1 2 Le2 2
2
( k V e )
Le
2 | E~tr (t , r ) |2
k 2
2
S tr (t , r )
c V e 2
( k 2V 2e )
8
6.
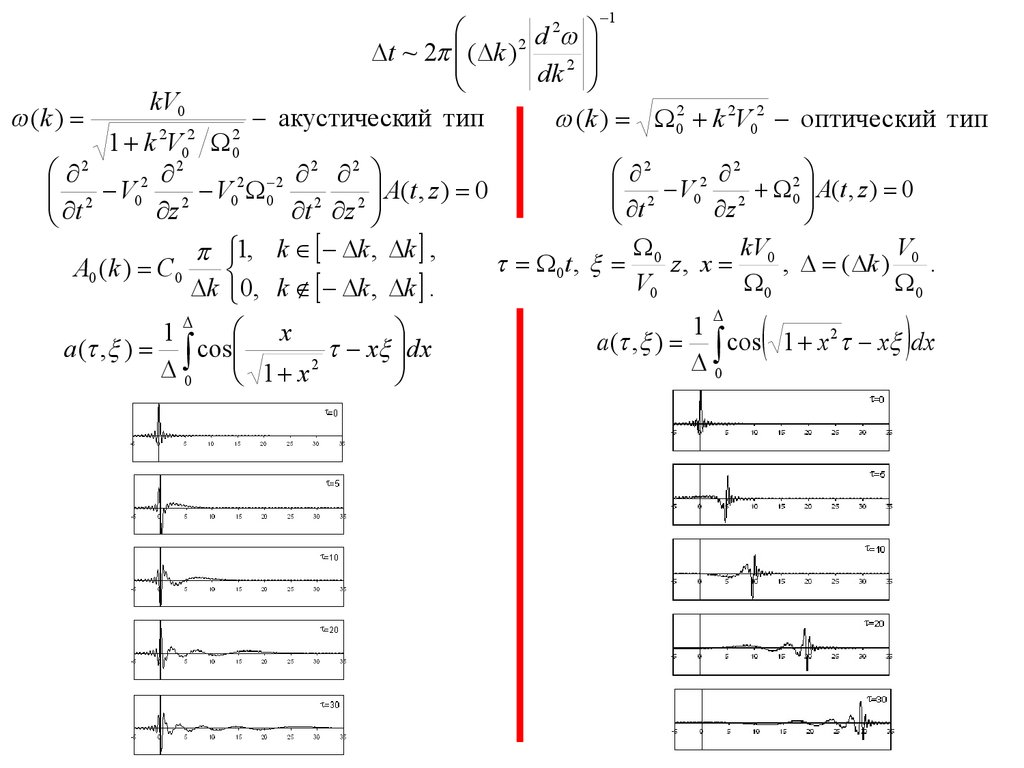
(k )kV0
1
d
t ~ 2 ( k ) 2
2
dk
акустический тип
(k ) 02 k 2V02 оптический тип
2
1 k 2V02 02
2
2
2
2
2
2 2
2 V0 2 V0 0
A(t , z ) 0
2
2
z
t z
t
1, k k , k ,
0t ,
A0 (k ) C0
k 0, k k , k .
x
1
dx
a ( , ) cos
x
2
0
1 x
2
2
2
2 V0 2 02 A(t , z ) 0
z
t
kV
V
0 z, x 0 , ( k ) 0 .
V0
0
0
1
a( , ) cos 1 x 2 x dx
0
7.
b(b )
I ( ) P (q ) exp i (q ) dq
x ( x ) I ( )
a
2
(q0 )
23
0 V0
k0 ( )
1
V0
1
1
P (q0 ) exp i (q0 ) (q q0 ) 2 (q0 )
2
1
A(t , z )
A0 (k ) exp it (k ) dk ,
2
A(t , z )
( x) exp(i x)dx ~
(a)
(q0 ) 0
I ( )
P( x)
12
12
P(q0 ) exp i (q0 ) i
4
(k ) k
z
(k )
t
d z
Vg ( k ) 0
dk t
2
0 V0
k0 ( )
1
V0
1 2
d 2
A0 ( k0 )
exp i (k 0 )t ik0 z i , G (k 0 ) 2
, k0 k0 ( z t )
4
2 t | G (k 0 ) |
dk k k0
dk0
1
dz t | G (k0 ) |
zt




 Математика
Математика Физика
Физика








