Похожие презентации:
Дифракция света на акустических волнах. Качественный анализ
1. 3. Дифракция света на акустических волнах
3.1. Качественный анализдифракции света на
акустических волнах
2.
Сточки
зрения
квантовой
механики
дифракцию
света
на
акустических волнах можно рассматривать как процесс трехчастичного
взаимодействия, когда фотон с энергией hωn и квазиимпульсом
взаимодействует с фононом
, K
kn
. В результате рождается фотон
дифрагированной волны, энергия и квазиимпульс которого должны
удовлетворять законам сохранения:
g n ,
(3.1)
kg kn K .
(3.2)
Первое из этих равенств всегда является точным и описывает с
классической точки зрения доплеровский сдвиг в дифрагированной волне,
обусловленный движением фазовой решетки (акустической волны).
3.
Второе равенство не всегда выполняется точно, может существоватьвектор k , выражающий рассогласования волновых векторов
k kn K k g . Это связано в первую очередь с тем, что реальные
оптические и акустические пучки являются ограниченными по апертуре и
описываются набором волновых векторов вблизи центрального вектора
k g 0 , k n 0 или K 0 (рис. 3.1).
k0
Рис. 3.1.
4.
Угол, в котором сосредоточена основная энергия волны,
определяется угловой расходимостью вследствие дифракции:
a
,
(3.3)
где –длина волны, а – апертура пучка.
При точном синхронизме имеем одно скалярное и одно векторное
условие трехчастичного взаимодействия (условия синхронизма):
g n ,
(3.4)
kg kn K .
(3.5)
5.
Вид треугольника волновых векторовkg , kn
и
K
зависит от
типа дифракции. Если длины волновых векторов световых волн не
зависят от их направления, что возможно в изотропной среде или для
обыкновенных волн в анизотропной среде, то этот треугольник
является равнобедренным.
Действительно, неравенство
g , n
соотношению
n
c
nn k n k g
g
c
ng ,
поскольку nn = ng = n не зависят от направления.
(3.6)
приводит к
6.
Векторная диаграмма для такой «изотропной» (обычной) дифракцииизображена
на рис. 3.2.
положениям концов векторов
Здесь
kn
сфера
и
соответствует
kg
, отложенных из начала
координат и называется поверхностью волновых векторов.
kg
Б
Б
kn
kg kn K
Рис. 3.3.
возможным
K
7.
Угол между волновым вектором падающей волныkn
и фронтом
акустической волны называется углом Брэгга и может быть легко найден
из рис. 3.2:
sin Б
K
2 kn
2 n
2va n
f.
(3.7)
Напомним, что подобное соотношение для дифракции рентгеновских
лучей на атомных плоскостях в кристаллах встречалось в курсе «Физика»
(Λ ↔ d, где d – межплоскостное расстояние).
На частотах до 3 ГГц угол
Б
мал, и синус можно заменить
аргументом. В этом случае для угла дифракции между
имеем
vа n
f.
(3.8)
k n и k g 2 Б
8.
Отметим важные следствия из нашего качественного рассмотрения:Сдвиг частоты в дифрагированной волне на частоту акустической
1.
волны можно использовать для частотной модуляции световых пучков.
Изменением амплитуды акустической волны можно модулировать
2.
амплитуду дифрагированного света.
Изменением частоты акустической волны f можно сканировать по
3.
углу
θ
световым
пучком
(сценические
эффекты,
телевизионные
изображения большой яркости, оптическая локация и т.д.).
4.
При заданных
измерять
частоту
, va
и n измерением угла
неизвестных
сигналов,
приходящих
можно
на
АОМ
(акустооптические анализаторы спектра и частотомеры).
5.
При заданных
n, va
и f можно проводить спектральный анализ
световых пучков и спектральную фильтрацию.
9.
В анизотропной среде возможна так называемая аномальнаядифракция Брэгга, когда падающая и дифрагированная волны имеют
разные типы, т.е. одна из них является обыкновенной, а другая –
необыкновенной (рис. 3.3).
x
K
kg
kn
z
10.
На данном рисунке падающая волна является обыкновеннойn( ) n0
, а дифрагированная – необыкновенной, с показателем
преломления n '( ) const .
Обыкновенная и необыкновенная волны, распространяющиеся в
одном
направлении,
имеют
ортогональные
(собственные векторы). Поскольку угол
векторы
поляризации
мал, то в изображенном
случае можно приближенно считать, что падающая и дифрагированная
волны ортогонально поляризованы по отношению друг к другу.
Аномальную дифракцию называют еще и дифракцией света с
поворотом плоскости поляризации, а также анизотропной дифракцией.
Отметим,
что
треугольник
волновых
существенно отличаться от равнобедренного.
векторов
здесь
может
11.
Частным случаем аномальной дифракции является коллинеарнаядифракция, когда волновые векторы всех взаимодействующих волн
параллельны друг другу (рис. 3.4).
kn
K
kg
Рис. 3.4
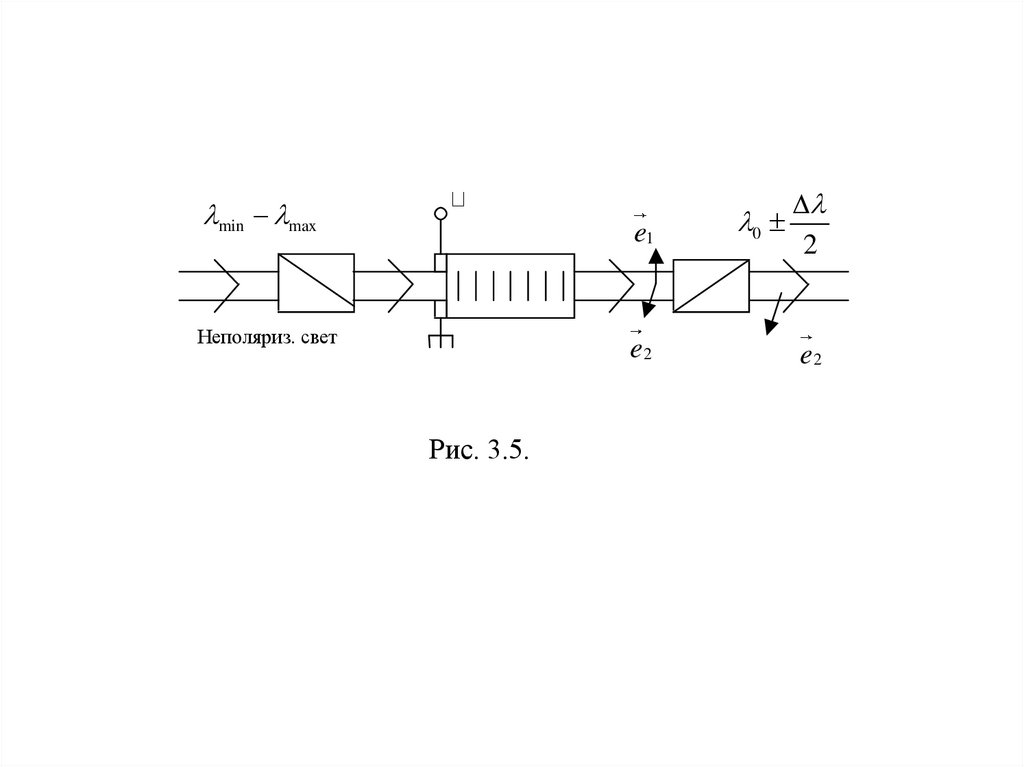
12.
Этот вид дифракции позволяет реализовать спектральные фильтры сшириной полосы пропускания
~ 5 Å (рис. 3.5), перестраиваемые при
изменении частоты акустической волны:
0
va
n0 n ' .
f
(3.9)
13.
min maxe1
Неполяриз. свет
e2
Рис. 3.5.
0
2
e2
14.
Количественный анализ эффектов дифракции света наакустических волнах рассмотрим ниже, используя несколько
подходов.
Начнем с подхода, в котором акустооптический модулятор
(АОМ) является «тонким» фазовым транспарантом. В этом
случае дифракционная картина содержит набор дифракционных
максимумов и называется дифракцией Рамана-Ната.
15. 3.2. Дифракция Рамана-Ната
При возбуждении АОМ монохроматическим сигналом егофункция пропускания на низких частотах (< 100 МГц) может быть
выражена в виде
2
TE ( x) PD ( x)exp i m cos t
x ,
где PD – апертурная функция модулятора.
(3.10)
16.
Если такой модулятор расположить в передней фокальной плоскостиР1 линзы Л, и пропустить через него плоскую световую волну
(3.11)
E ( z, t ) E0 exp i( 0t kz ) ,
то поле Е2 в задней фокальной плоскости Р2 будет выражаться
интегралом Фурье
E2 ( x2 , t )
T ( x , t ) E ( z d , t )exp(i
E
1
x )dx1
x2 1
E0 exp i ( 0t kdn0 )
2T1
exp
i
cos
t
x
m
1
exp(i x 2 x1 )dx1
D 2
D 2
, (3.12)
где m (2 ) nm d , nm – амплитуда изменения коэффициента
преломления материала АОМ под действием акустической волны.
17.
Разлагая в ряд по функциям Бесселя функцию exp(i m cos ) , послепреобразований получаем поле Е2 в виде
E2 ( x2 , t ) E0 exp( ikn0 d ) exp i ( 0 m )t m m
2
m
2
D
sin
m x 2
2
J m ( m )
,
2
D
m x 2
2
(3.13)
m 0, 1, 2,...
Таким образом, световое поле в фокальной плоскости линзы при
дифракции Рамана-Ната представляет собой набор дифракционных
максимумов, причем положение m-го определяется формулой
x2 m n0 F m
va
fFm .
(3.14)
18.
Амплитуда световой волны в m-м дифракционном максимумеопределяется функцией Бесселя m-го порядка от аргумента
m
,
пропорционального амплитуде деформаций в акустической волне.
Для m = ±1, при m 1 , имеем J 1 m 2 , что дает линейную
зависимость амплитуды дифрагированного света от амплитуды
акустической волны. Отметим также сдвиг частоты в m-м максимуме
на величину mΩ и наличие сдвига фазы mφ, определяемого начальной
фазой сигнала, возбудившего акустическую волну.
Применение дифракции Рамана-Ната ограничено ввиду множества
дифракционных максимумов.
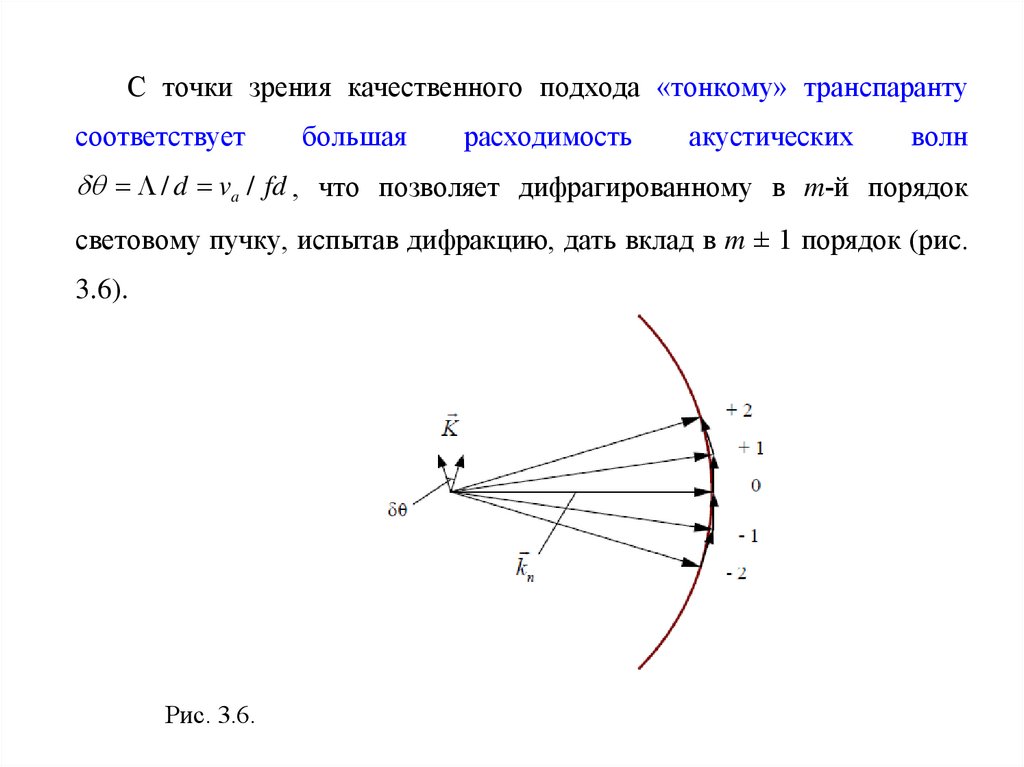
19.
С точки зрения качественного подхода «тонкому» транспарантусоответствует
большая
расходимость
акустических
волн
/ d va / fd , что позволяет дифрагированному в m-й порядок
световому пучку, испытав дифракцию, дать вклад в m ± 1 порядок (рис.
3.6).
Рис. 3.6.
20. 3.3. Дифракция Брэгга в изотропной среде. Метод волнового уравнения
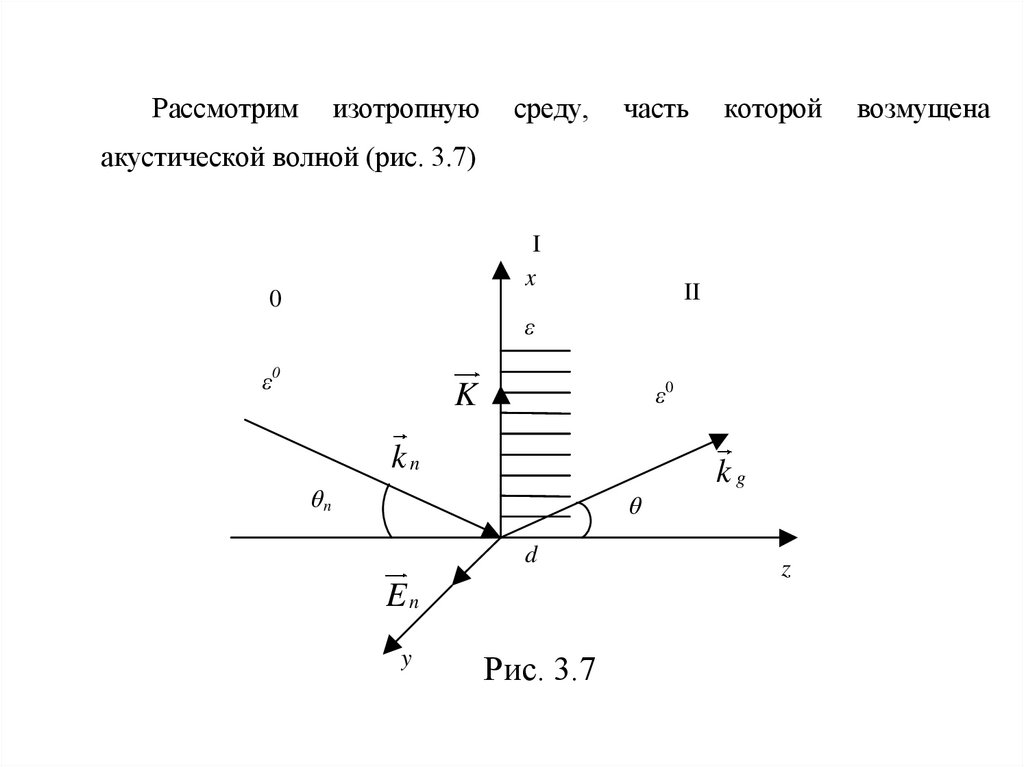
21.
Рассмотримизотропную
среду,
часть
которой
акустической волной (рис. 3.7)
I
x
0
II
ε
ε0
ε0
K
kn
kg
θn
θ
d
En
y
Рис. 3.7
z
возмущена
22.
Здесь относительная диэлектрическая проницаемость среды может бытьпредставлена в виде
r r0 m cos( t Kx ) , при 0 z d ,
0
где r
(3.15)
– диэлектрическая проницаемость невозмущенной среды; m –
амплитуда изменения диэлектрической проницаемости акустической
волной; φ – начальная фаза акустической волны.
Пусть плоская монохроматическая световая волна с волновым вектором
k n , лежащим в плоскости xz, и поляризованная вдоль оси y, падает на
акустический пучок.
Очевидно, если угол θn близок к углу Брэгга, то возникает за счет
дифракции на неоднородностях дифрагированная волна с волновым
вектором k g .
Отметим, что угол θ не обязательно может быть равен θБ.
23.
Количественное рассмотрениедифракции
может
Брэгга
быть
проведено на основе волнового уравнения.
2
E 0 0 2 ( r E) 0 ,
t
2
(3.16)
где μ0 и ε0 – магнитная и диэлектрическая проницаемости вакуума. Для
z 0 решение волнового уравнения хорошо известно и в нашем случае
может быть представлено в виде
0
exp i ( nt knx x knz z ) к.с. ,
E n y0 Enm
0
0
const
Enm
где
kn
на оси x и z, соответственно;
преломления невозмущенной среды.
амплитуда
–
knx 2 n0 sin n , knz 2 n0 cos n
вектора
(3.17)
–
проекции
n0 r0
волны;
волнового
– коэффициент
24.
Из физических соображений ясно, что в пределах акустического пучкабудет происходить изменение амплитуды падающей волны за счет
передачи
энергии
дифрагированной
волне.
Поэтому
целесообразно
решение для падающей волны в возмущенной среде искать в виде
E n y0 Enm ( z )exp i( nt knx x knz z ) к.с.
I
(3.18)
Считаем здесь, что knx и knz такие же, как и для невозмущенной среды.
По аналогии запишем и решение для дифрагированной волны
I
E g y0 E gm ( z )exp i( g t k gx x k gz z ) к.с.,
где k gx (2 ) n0 sin , k gz (2 ) n0 cos .
(3.19)
25.
Очевидно, что амплитуды волн Enm(z) и Egm(z) удовлетворяютграничным условиям
0
Enm ( z ) Enm
z 0
E gm ( z ) 0 z 0 .
,
(3.20)
(3.21)
26.
Частотывзаимодействующих
волн
будем
считать
удовлетворяющим условию синхронизма
g n .
Кроме
того,
(3.22)
будем
предполагать
выполнение
векторного синхронизма для проекций векторов
условий
kn, K и kg
на
ось x:
k gx knx K ,
(3.23)
а на проекции этих векторов на ось z пока никаких ограничений не
накладываем.
27.
Теперь мы можем подставить решение для поляI
g
I
n
E E E в волновое уравнение (3.16) и учесть выражение
для εr при 0 z d из (3.15), расписывая его через экспоненты
по формуле Эйлера.
28.
В результате получаем, опуская y0 :d E nm d 2 E mn
2
2
2 2
knx knz 0 0 n0 n E mn 2iknz dz dz
exp i ( nt knx x knz z )
2
d
E
d
E mg
gm
2
2
2 2
k gx k gz 0 0 n0 g E gm 2ik gz
dz
dz
exp i ( g t k gx x k gz z )
m
0 0
( n ) 2 Enm
2
exp i ( n )t (knx K ) x knz z 0 0 ( n ) 2 Enm
exp i ( n )t (knx K ) x knz z 0 0 ( g ) 2 E gm
exp i ( g )t (k gx K ) x k gz z 0 0 ( g ) 2 Egm . (3.24)
exp i ( g )t (k gx K ) x k gz z
29.
В этом выражении подчеркнем члены, которые находятся в резонанседруг с другом, с учетом условий (3.22) и (3.23); найдем, что
удовлетворяются соотношения
knx2 knz2 0 0 n 2 2 0 , k gx2 k gz2 0 0 n2 2 0 ,
а также будем считать малыми вторые производные от амплитуд волн:
2
dEgm
d 2 Enm
dEnm d Egm
k gz
,
.
knz
2
2
dz
dz
dz
dz
30.
Последниенеравенства
используются
в
методе
медленно
меняющихся амплитуд для получения укороченных уравнений, в
которых ими пренебрегается
dEmn
m k02
i
Egm exp( i kz ) exp( i ) ,
dz
4knz
dEmg
dz
i
m k02
4k gz
Enm exp(i kz ) exp(i ) ,
(3.25)
(3.26)
где k k gz knz .
Здесь мы приравняли члены в правой и левой частях (3.24),
находящиеся в резонансе, и отбросили нерезонансные члены.
31.
Уравнения (укороченные) (3.25) и (3.26) называютуравнениями связанных волн.
Они показывают, что при дифракции света на
акустических волнах изменение амплитуды волн в
пространстве пропорционально амплитуде «связанной»
волны и амплитуде акустической волны.
32.
Длянахождения
решений
для
амплитуд
падающей
и
дифрагированной волн из уравнений связанных волн (3.25) и (3.26),
являющихся обыкновенными дифференциальными уравнениями первого
порядка, сведем ее к одному уравнению второго порядка. Для этого
выразим из (3.26) амплитуду падающей волны Enm ( z ) :
Emn
exp( i kz ) exp( i ) dEgm
.
i m k02 (4k gz )
dz
(3.27)
Далее, отыскивая производную этой функции,
dEgm d 2 Egm
dEnm
exp( i )
exp( i kz ) ,
i k
2
2
dz
i m k0 (4k gz )
dz
dz
подставим результаты в (3.25).
33.
В результате получаем следующее линейное дифференциальноеуравнение второго порядка с постоянными коэффициентами:
d 2 E gm
dz
2
i k
dE gm
dz
m2 k04
16k gz k nz
E gm 0 .
(3.28)
Его решение имеет вид
Egm ( z ) A exp( p1 z ) B exp( p2 z ) ,
(3.29)
где p1,2 – корни характеристического уравнения
p 2 i kp 2 0 ,
(3.30)
2
2 4
в котором введено обозначение m k0 (16k gz k nz ) .
34.
Выражая эти корни в видеp1,2
i
k k 2 4 2
2
(3.31)
и используя граничное условие (3.21), из (3.29) получаем решение для
амплитуды дифрагированной волны
1
k
E gm ( z ) A0 sin
k 2 4 2 z exp i
2
2
известное с точностью до постоянной A0.
z ,
(3.32)
35.
Амплитуду падающей волны найдем, подставляя решение (3.32) вуравнение (3.27):
Enm ( z ) A0
exp i kz / 2 exp( i )
i m k02 (4k gz )
1
1
k
1
k 2 4 2 cos k 2 4 2 z i
sin k 2 4 2 z .
2
2
2
2
(3.33)
Используя далее граничное условие (3.20), находим постоянную A0:
m
exp(i )
0
A0 iEnm
.
2
2
2 cos n k 4 / 2
(3.34)
36.
В результате выражения для амплитуд Еgm(z) и Enm(z) могут бытьполучены в виде
m
k
Egm ( z ) iE
z exp i
2
2 cos n
2
sin k 2 m n0 cos z / 2
k 2 n cos 2 z / 2
m
0
0
nm
z exp(i )
,
2
m
k 1
0
E nm ( z ) Enm
exp i
z cos
k 2
z
2 2
n0 cos
2
sin k 2 m n0 cos z / 2
k
i
z
,
2
2
k 2 n cos z / 2
m
0
(3.35)
(3.36)
37.
Здесь мы выразили 4 2 в виде2
m
( m ) 2 k02
2
4 2
,
4n0 cos cos n n0 cos
поскольку
n .
Выразим далее расстройку волновых векторов взаимодействующих
волн k через длину волны акустических колебаний и угол падения n :
38.
k k0 n0 (cos cos n ) k0 n01 sin cos
2
n
2
2
(knx K )
k0 n0 1
cos n k0 n0 1
sin n cos n
2 2
k0 n0
n0
2
2
2
k0 n0 (1 sin n ) 2 2
sin n cos n
n
n
0
0
1
k0 n0 cos n 1
2sin
cos
n
n
2
n0
2cos n n0
K
sin
n
.
cos n
2n0
При выводе (3.37) использовалось неравенство
2sin
n
n0
n0
cos n .
(3.37)
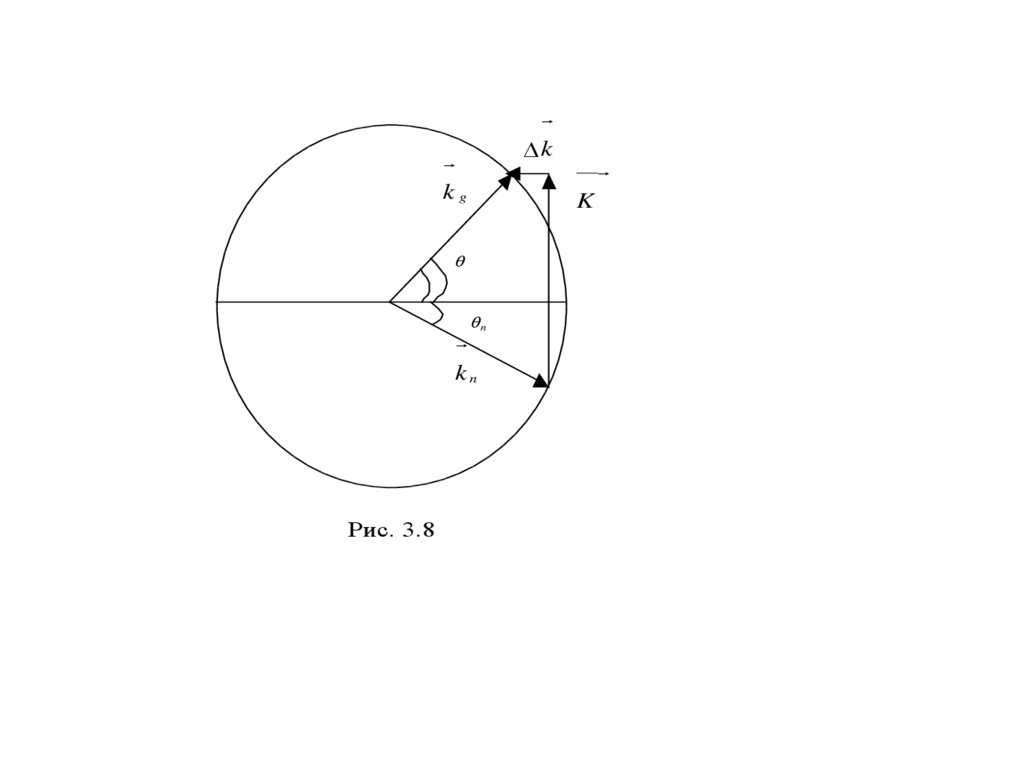
39.
Проведем ниже анализ полученных выражений, которыесправедливы также и для дифракции света на фазовых
голографических решетках с периодом Λ.
1. Вектор Δk определяет фазовую расстройку треугольника
векторов и от условия синхронизма
k k g k n K ,
(3.38)
см. рис. 3.8. Точный синхронизм наблюдается при выполнении
условия Брэгга, Δk = 0 при sin n sin Б 2 n0 .
40.
kkg
K
θ
θn
kn
Рис. 3.8
41.
В этом случае решения для Egm(z) и Enm(z) имеют простой вид:m
0
E gm ( z ) iEnm
exp(i )sin
,
2 cos n
(3.39)
m
Enm ( z ) E cos
.
2
cos
n
0
nm
(3.40)
Здесь происходит полный обмен энергией между падающей и
дифрагированной волнами при толщине фазовой решетки z = dm:
dm
cos n
.
m
(3.41)
42.
2. Выбор направления kпо нормам к границам слоя обеспечивает
автоматическое выполнение граничных условий для падающей и
дифрагированной волн при z = 0.
3. В случае акустической волны её начальная фаза переносится на
световую дифрагированную волну.
Этот эффект можно использовать для фазовой модуляции света,
для
построения
акустооптических
фазометров
и
пеленгаторов источников радиоизлучения (Egm(z) ~ exp(iφ)).
фазовых
43. 3.4 Анализ соотношений для дифрагированного светового поля
В выражении (3.35) можно выделить несколько сомножителей.Первый из них,
m
i E
2 n0 cos
0
nm
характеризует
z ,
амплитуду
k 2 m n0 cos z / 2 1.
2
дифрагированной
волны
при
44.
Она пропорциональна амплитуде падающей волны при z = 0,0
Enm
, амплитуде модуляции диэлектрической проницаемости среды
акустической волной δεm, и длине взаимодействия z.
Множитель –i показывает, что фаза дифрагированной волны
сдвинута относительно падающей волны, как минимум, на / 2 ,
без учета других фазовых сдвигов.
45.
Второй сомножитель,k
exp i
2
Kz
sin
z exp i
n
2n0
2cos n
(3.42)
fz
f
exp i
,
sin n
2va n0
va cos
характеризует
характеристику
фазочастотную
брэгговского
акустооптического взаимодействия.
Для
случая
точного
выполнения
условия
Брэгга,
sin n sin Б f (2va n) фазочастотный множитель равен единице.
46.
Третий сомножитель exp(iφ) показывает, что начальная фазаакустической волны переносится на дифрагированную световую волну.
Четвертый сомножитель,
sin k 2 m n0 cos z / 2
A( f )
,
2
k 2 n cos z / 2
m
0
2
характеризует амплитудно-частотную характеристику брэгговского
акустооптического взаимодействия.
47.
При условии «слабого» взаимодействия, когда выполняется условиеk
m
n0 cos
,
получаем
z
sin
sin n
cos
2
n
sin kz 2
n
0
. (3.43)
A( f ) ~
kz 2
z
sin n
cos
2
n
n
0
При точном выполнении условий Брэгга
A( f0 ) 1 .
Условия Брэгга нарушаются: при изменении частоты акустической
волны (частотная селективность акустооптического брэгговского
взаимодействия); при изменении угла падения θn (угловая селективность
дифракции Брэгга); при изменении длины волны света (спектральная
селективность дифракции Брэгга).
48.
Подбором параметров Λ, z, va , f можно изменять каждыйвид
селективности,
обеспечивая
или
широкополосную
дифракцию (частотная селективность), или, например, высокую
угловую
селективность
голограмм,
обеспечивающую
возможность записи большого числа голограмм в одном
кристалле.
49. 3.5. Эффективность дифракции Брэгга. Коэффициент акустооптического качества среды М2. Зависимость эффективности дифракции от
акустической мощностии размеров пьезопреобразователя
50.
Определим эффективность дифракции как отношение мощностидифрагированного
света
после
взаимодействия
к
мощности
падающего светового пучка до взаимодействия:
Eg (d )
0 2
( Enm
)
2
2
nm sin kd 2
d
2
cos kd 2
2
d
2
sin
sin
n
2
cos
2
n
nm
n
0
d
2
cos d
sin n
cos
2
n
n
0
d
f
2
sin
f sin n
2
v
cos
2
n
v
n
n
0 a
a
m
d
.
2
cos
d
f
f sin n
v
cos
2
n
v
n
0 a
a
(3.44)
51.
Здесьm 2n0 nm
мы
0
воспользовались
соотношением
m (n0 nm ) 2 , 0 n02 ; nm2 2n0 nm .
При выполнении условия Брэгга эффективность дифракции
максимальна и определяется выражением
nm
( Б ) m
d .
cos
2
(3.45)
52.
Воспользуемся далее соотношениями из теории акустическихволн в твердых телах:
n03
nm
pU m , U m
2
2 P0
3
0 va
2 Pa
,
3
0 va hd
(3.46)
где Um – амплитуда деформаций в акустической волне; p –
фотоупругая
постоянная
среды,
в
которой
происходит
акустооптическое взаимодействие; P0 – плотность акустической
мощности; 0 – плотность среды; h – ширина пьезопреобразователя;
Pa – полная акустическая мощность, излучаемая преобразователем
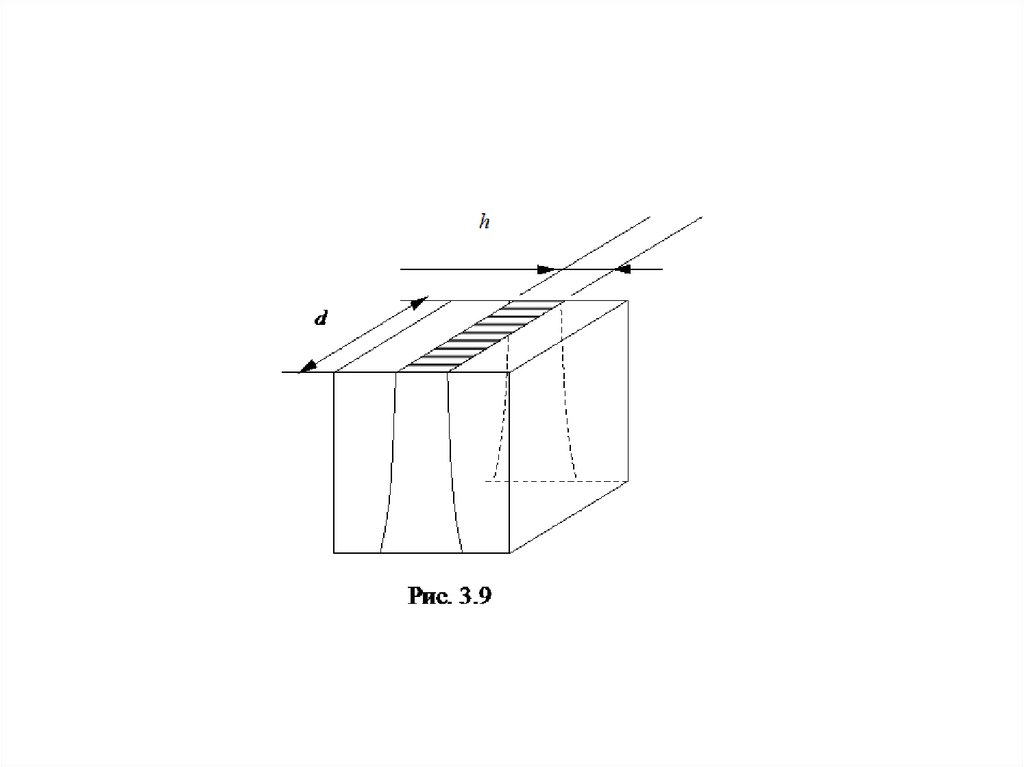
(рис. 3.9). С учетом (3.46) из (3.45) получаем
1
1 n06 p d
m
Pa .
2
3
2 cos va h
2
(3.47)
53.
54.
В этой формуле можно выделить сомножитель, зависящий только отфизических параметров акустооптического материала. Для общего случая
анизотропной среды имеем
M2
6
2
nэф
pэф
v
3
0 a
,
(3.48)
где nэф и pэф – эффективные показатель преломления и фотоупругая
постоянная для выбранного среза кристалла и геометрии взаимодействия.
Коэффициент
качества
среды
M2
является
важнейшей
характеристикой акустооптического материала. Обычно он измеряется по
отношению к M2 плавленого кварца, найденному при дифракции света на
продольной акустической волне, когда световая волна поляризована в
плоскости треугольника волновых векторов k n , k g и K .
55.
Для плавленого кварца в этом случае коэффициент качества M2 =1.56∙10-18 с3/кг. С помощью относительного коэффициента качества,
учитывая, что для большинства случаев cos 1, выражение (3.47)
можно привести к удобному для практических расчетов виду
2
1 0.63
d
m
M
P
,
2r a
54
h
(3.49)
где Pa измеряется в Вт, λ – в мкм, M2r – в относительных единицах.
Заметим, что подобное выражение справедливо и для анизотропных
сред, однако при этом M2r сложным образом зависит от фотоупругих,
упругих, электрооптических, и других констант материала.


















































 Физика
Физика








