Похожие презентации:
Производная функции
1.
Математикагруппа 201
Производная
функции
Преподаватель Морозова И.М.
2. Домашнее задание
1. Изучить презентацию.2. Выписать в тетрадь примеры решения задач из данной
презентации.
3. Выполнить тест в тетради в конце презентации. Фото теста
прислать на почту idenm@ya.ru. Вариант – номер вопросаномер ответа. В письме написать ФИО и номер группы.
4. Все вопросы по теме и выполнению данных заданий можно
задавать в WhatsApp или Viber по номеру 8-912-61-85-301.
3.
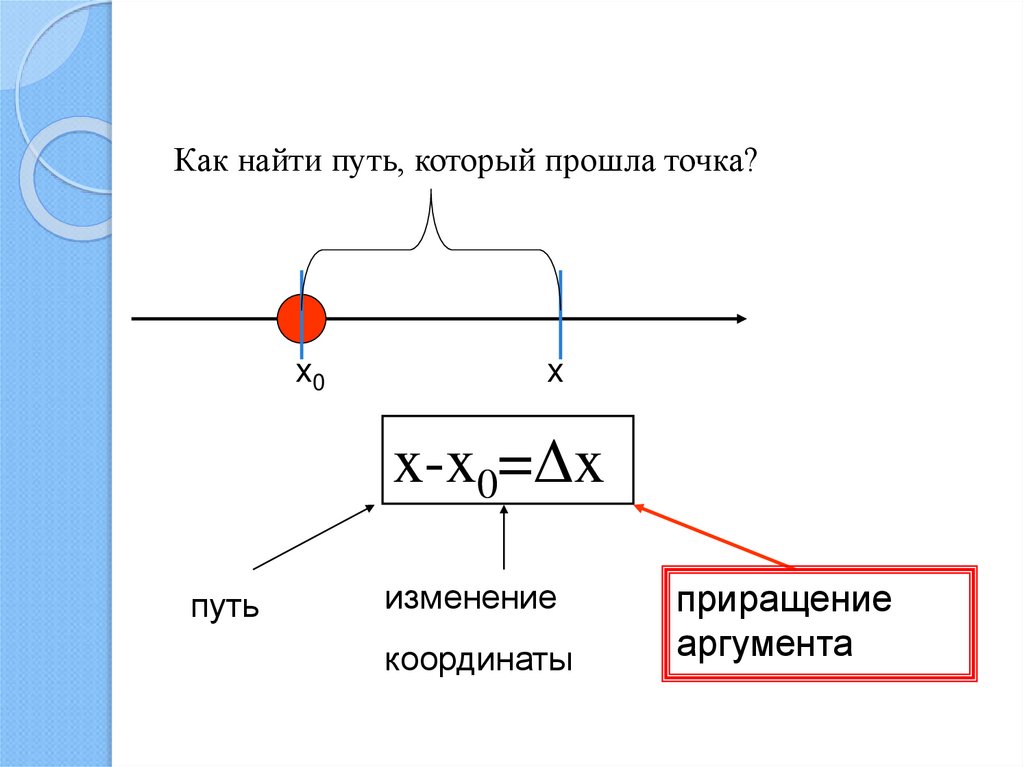
Как найти путь, который прошла точка?x0
x
x-x0=Δx
путь
изменение
координаты
приращение
аргумента
4.
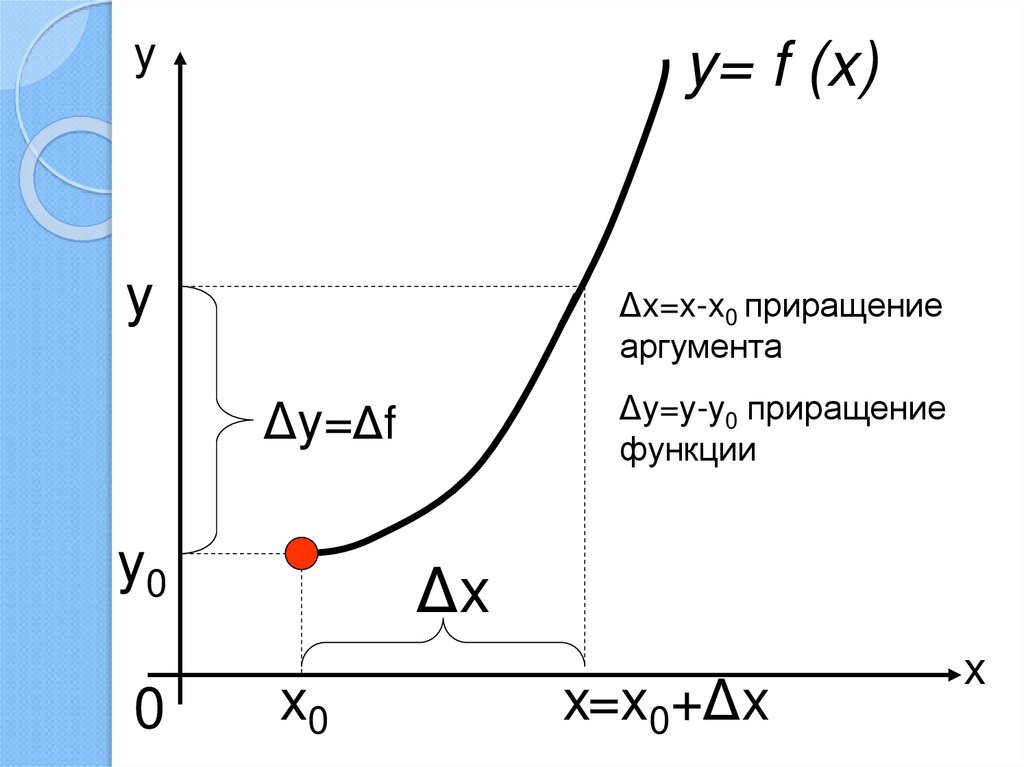
yy= f (x)
y
Δx=x-x0 приращение
аргумента
Δy=y-y0 приращение
функции
Δy=Δf
y0
0
Δx
x0
x=x0+Δx
x
5.
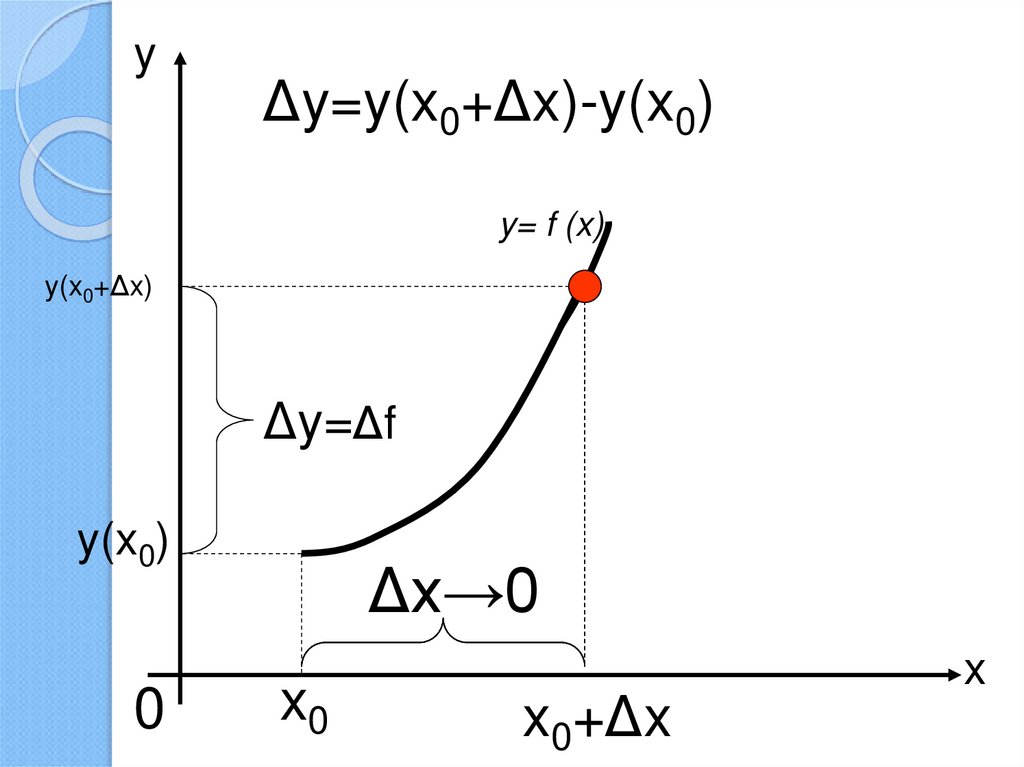
yΔy=y(x0+Δx)-y(x0)
y= f (x)
y(x0+Δx)
Δy=Δf
y(x0)
0
Δx→0
x0
x
x0+Δx
6.
ОпределениеПроизводной функции называется предел отношения
приращения функции к приращению аргумента, когда
приращение аргумента стремится к нулю.
y ( x0 x) y ( x0 )
y
y lim
lim
x 0 x
x 0
x
Обозначение
y
или
f (x )
7.
Схема вычисления производной функции1. Найти приращение функции на отрезке [ x; x+Δx]:
y y ( x x) y ( x)
2. Разделить приращение функции на приращение
аргумента: y
y ( x x) y ( x)
x
x
3. Найти предел отношения приращения функции к
приращению аргумента, когда приращение аргумента
стремится к нулю.
y
y ( x x) y ( x)
y lim
lim
x 0 x
x 0
x
8.
Пример: Вычислить производную функции y=x2Решение: Используем схему вычисления производной по
действиям:
1.
y y ( x x) y ( x) ( x x) x
2
2
x 2 2 x x x 2 x 2 2 x x x 2
2.
3.
y 2 x x x
x (2 x x)
x
x
x
2
2x x
y
y lim
lim 2 x x
x 0 x
x 0
lim 2 x lim x 2x 0 2x
x 0
x 0
9.
Задание: Найти производную функции:1.
y x
2.
y C , где С число
Решение 2
3.
y kx b, где k и b числа
Решение 3
4.
5.
3
Решение 1
y ax , где a число
2
1
y
x
Решение 5
6.
Решение 4
y x
Решение 6
10.
y (функция ) y (производная функции )y x
3
y C , где С число
3x
2
0
y kx b, где k и b числа
k
y ax , где a число
2ax
2
1
y
x
y x
1
x2
1
2 x
11.
Решение 1: Вычислить производную функции y x 31.
y y ( x x) y ( x) ( x x) x
3
3
x 3 3x 2 x 3x x 2 x 3 x 3
3x 2 x 3x x 2 x 3
2.
3.
y 3x 2 x 3x x 2 x 3
3x 2 3x x x 2
x
x
y
2
2
y lim
lim 3x 3 x x x
x 0 x
x 0
2
2
lim 3x lim 3x x lim x
x 0
2
x 0
3x 0 0 3x
x 0
2
Задания
12.
Решение 2: Вычислить производную функции y C , где С число1.
2.
3.
y y ( x x) y ( x) С С 0
y
0
0
x x
y
y lim
lim 0
x 0 x
x 0
0
Задания
13.
Решение 3: Вычислить производную функции y kx b, где k и b числа1.
y y ( x x) y ( x) k x x b kx b
kx k x b kx b k x
2.
3.
y k x
x
x
k
y
y lim
lim k
x 0 x
x 0
k
Задания
14.
Решение 4: Вычислить производную функции1.
y y ( x x) y ( x)
y ax 2 , где a число
a( x x) ax
2
2
a( x 2 2 x x x 2 ) ax 2
ax 2 2ax x a x 2 ax 2 2ax x a x 2
2.
y 2ax x a x 2
x (2ax a x)
x
x
x
2ax a x
3.
y
y lim
lim (2ax a x)
x 0 x
x 0
lim 2ax lim a x 2ax 0 2ax
x 0
x 0
Задания
15.
1y
Решение 5: Вычислить производную функции
x
1
1
y y ( x x) y ( x)
x x x
1 x
1 ( x x) x x x x
x( x x) x( x x)
x( x x) x( x x)
1.
2.
3.
x
y
1
x
x( x x)
2
x
x x x
x( x x) x
x
y
1
1
1
y lim
lim ( 2
) 2
2
x 0 x
x 0 x x x
x 0 x
Задания
16.
y xРешение 6: Вычислить производную функции
1.
y y ( x x) y ( x)
2.
y
x
x x x
x
x x x
x x x x x x
x x x x
x x x
x
1
x x x x x x x x x x x
3.
y
1
y lim
lim (
)
x 0 x
x 0
x x x
1
1
x 0 x 2 x
Задания
17.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИСложная функция: y g f x .
1) y 3 x 2 x .
Примеры:
5
2
2) y sin x . y f ;
f sin x.
y f 5;
f 3 x 2 2 x.
3) y cos 2 x .
3
y cos f ;
f 2x .
3
Правило нахождения производной сложной функции
g
/
f x g f f x
/
/
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
18.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИСложная функция: y g f x .
Правило нахождения производной сложной функции
g / f x g / f f / x
Простая
функция
Производная
простой
функции
xn
nx
1
x
1
2
x
x
2 x
sin x
cos x
n 1
1
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Сложная Производная сложной функции
функция
f n x
1
f x
f x
sin f x
n f n 1 x f / x
f / x
f 2 x
f / x
2 f x
cos f x f / x
19.
1)y = x•cos xНайти у´
y´=(x•cos x)´= x´•cos x + x•(cos x)´=1•cos x + x•(-sin x)= cos x - x•sin x
2)y = x5+sin x
Найти у´
y´=(x5+sin x)´= (x5)´+(sin x)´= 5x4+cosx
3) y = x•sin x
Найти у´
y´=(x•sin x)´= x´•sin x + x•(sin x)´=1•sin + x•cos x= sin x + x•cos x
4) y = 4 x +tg x
Найти у´
y´=(4 x +tg x)´= (4 x )´+(tg x)´= 4
5) y = sin x –2х
1
2 х
Найти у´(0)
y´=(sin x - 2x)´= (sin x)´-(2x)´= cosx - 2
у´(0) = cos 0 - 2 = 1-2 = -1
+
1
cos 2 x
=
2
х
+
1
cos 2 x
20.
Производная сложнойфункции
Функция h есть
сложная функция, составленная
из функций g и f, если
h(x)=g(f(x))
f(x) – «внутренняя функция»
g(f) – «внешняя функция»
21.
Определим внутреннюю(f) и внешнюю(g)элементарные функции, из которых составлена
сложная функция h(x)=g(f(x))
h(x) = cos3x
f(x) = 3x
g(f) = cosf
1)
h(x) = tg(2x- /4)
f(x)= 2x- /4
g(f) = tgf
2)
h(x)=(3-5x)5
f(x) = 3-5x
g(f) = f 5
4) h(x) = sin x
f(x) = sin x
g(f) = f
3)
22.
Определите внутреннюю(f) и внешнюю(g)элементарные функции, из которых составлена
сложная функция y=g(f(x))
1) y = 9-x2
2) y = sin
x
3
3) y = 2(3x3-6x)7
f(x)= 9-x2,
f(x)=
x
3
,
f(x)= 3x3-6x,
g(f)= f
g(f)=sin f
g(f)=2f 7
23.
Формула производной сложнойфункции
.
h΄(x) = g´(f) f ´(x)
24.
h΄(x) = g´(f) • f ´(x)Алгоритм нахождения производной
сложной функции
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f
3)
Найди производную внешней функции g´(f)
4)
´(x)
Перемножь производные внутренней и внешней
функции и получишь производную сложной
функции
h΄(x) = f ´(x) • g´(f)
25. Производная сложной функции
Задание 1. Найдите производную функцииh(x) = (2x+3)100
1. Определим внутреннюю(f)и внешнюю(g) функции
f(x)=2x+3
g(f)=f 100
2. Найдем производную внутренней функции
f ´(x)=(2x+3)´=2
3. Найдем производную внешней функции
g´(f)=(f 100)´=100 f 99
4. Перемножим производные внутренней и внешней
функций
h´ (x) = 2 . 100 f 99= 200 f 99 = 200(2x+3) 99
26. Определим внутреннюю(f) и внешнюю(g) элементарные функции, из которых составлена сложная функция h(x)=g(f(x))
Задание 2. Найдите производную функцииy(x) =4cos 3x
1. Определим внутреннюю(f)и внешнюю(g) функции
f(x)=3x
g(f)=4cosf
2. Найдем производную внутренней функции
f ´(x)=(3x)´=3
3. Найдем производную внешней функции
g´(f)=(4cosf)´= - 4sin f
4. Перемножим производные внутренней и внешней
функций
y´ (x) = 3 .( - 4sin f) = - 12sin f = - 12sin3x
27.
Задание 3. Найдите производную функцииa) y= 9 х
2
a) f(x)=9-x2, g(f)= f
f ´(x)=(9-x2)´= -2x
g´ (f)=( f )´=
1
х
б) у= 6sin 3
х
б) f(x)=
, g(f)= 6sin f
3
f ´(x)=( х ) ´= 1
3
3
2 f
g´ (f)=(6sin f)´=6cos f
2x
y ´ = -2x
==
2 f
2 f
1
y´ = .6cos f = 2cos f=
3
x
=f
х
= 2cos
3
1
=
x
9 x2
28.
Тест29.
1 вариантА
В
С
1.
2.
3
4.
5.
2 вариант
1
2
3
4
5
А
В
С
30.
Многие, которым никогда не представлялосьслучая более узнать математику, смешивают
ее с арифметикой и считают ее наукой сухой.
В сущности же эта наука, требующая
наиболее фантазии, и один из первых
математиков нашего века говорит совершенно
верно, что нельзя быть математиком, не
будучи в то же время поэтом в душе.
С. КОВАЛЕВСКАЯ
Благодарю за внимание!
Учитесь с удовольствием!



















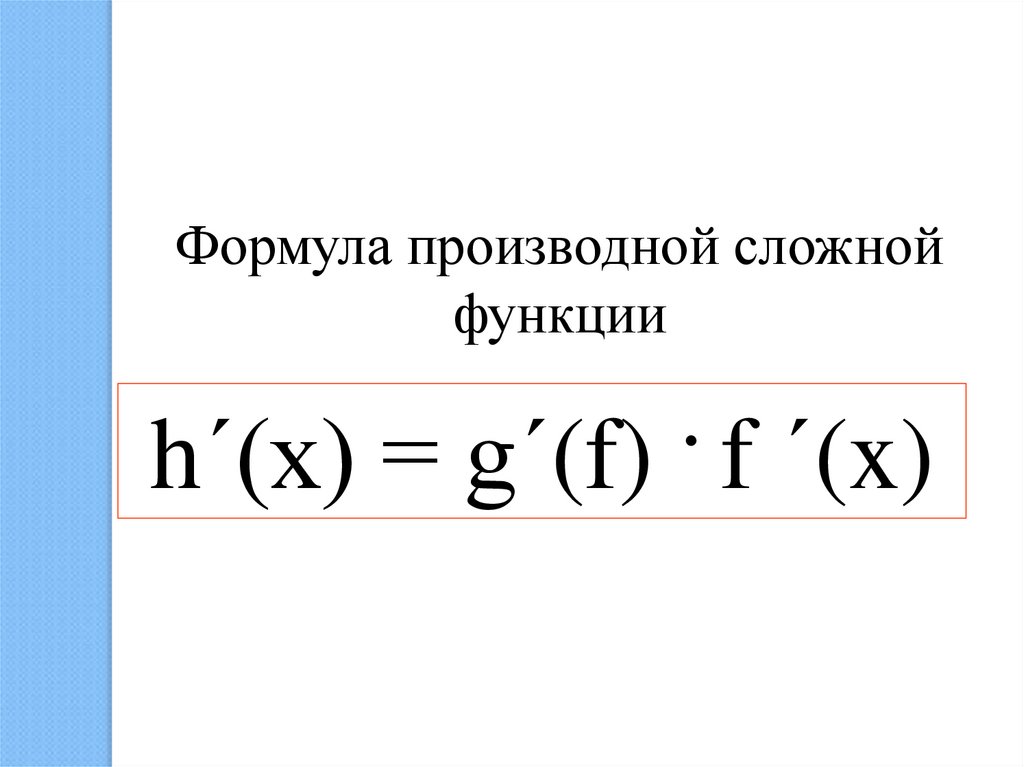







 Математика
Математика








