Вписанная окружность в треугольник

1. ГЕОМЕТРИЯ

30 апреля
Повторить определение вписанной окружности,
Решит №552,553
Тетради сдать до 2 мая

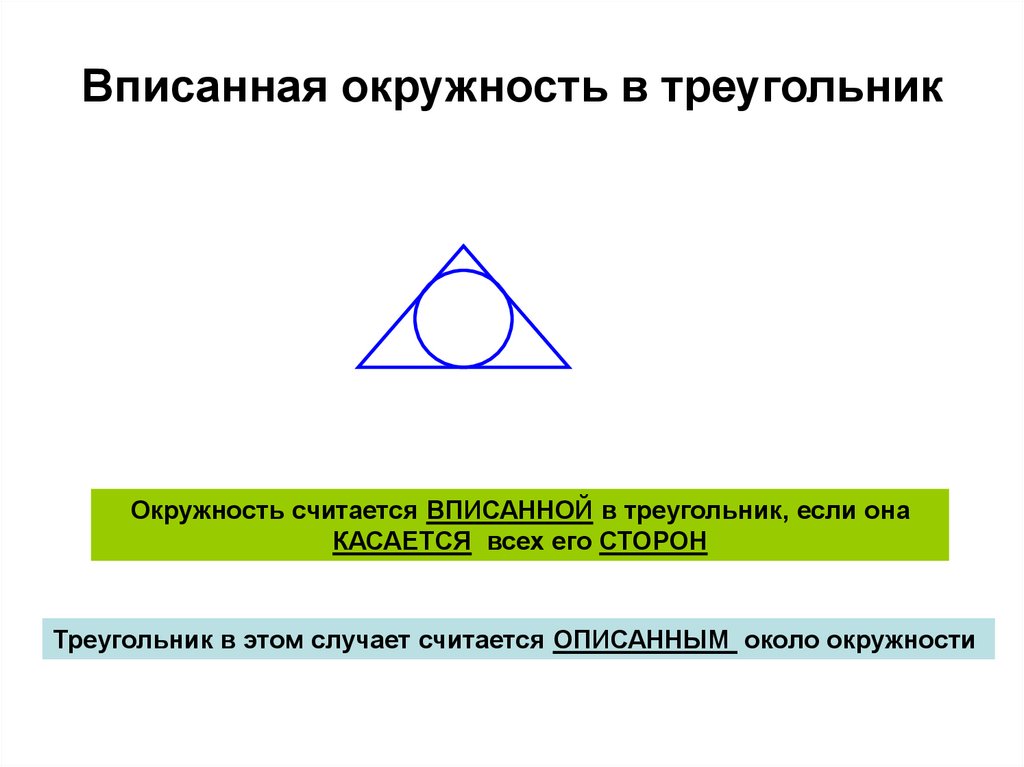
2. Вписанная окружность в треугольник

Окружность считается ВПИСАННОЙ в треугольник, если она
КАСАЕТСЯ всех его СТОРОН
Треугольник в этом случает считается ОПИСАННЫМ около окружности

3.

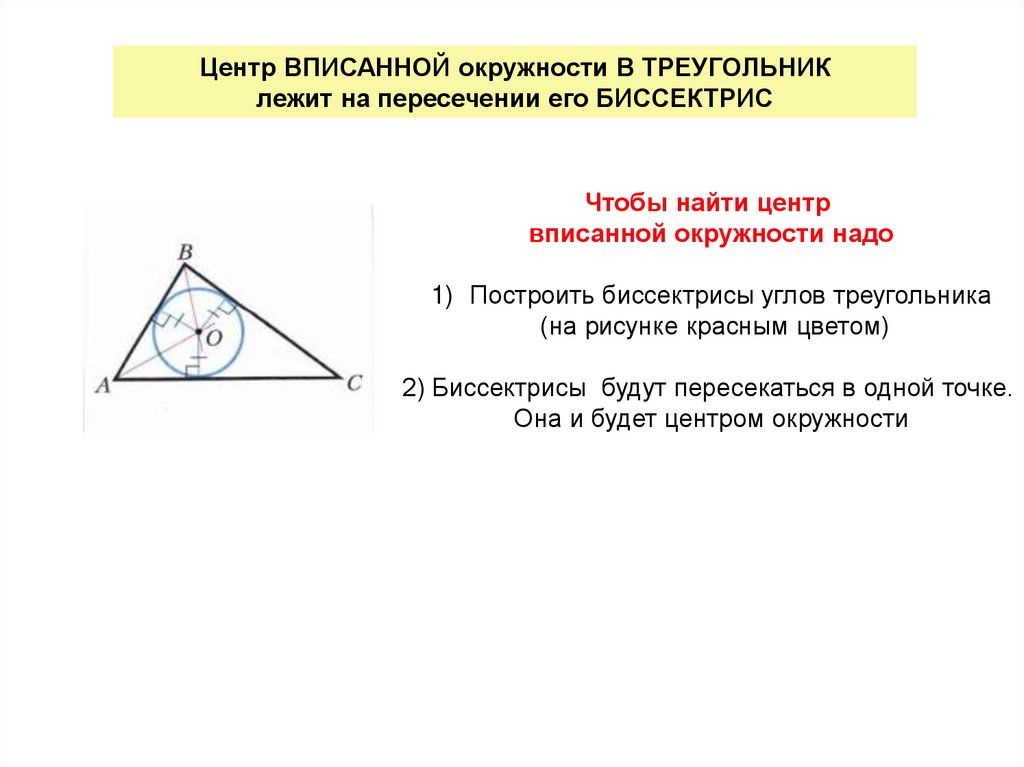
Центр ВПИСАННОЙ окружности В ТРЕУГОЛЬНИК
лежит на пересечении его БИССЕКТРИС
Чтобы найти центр
вписанной окружности надо
1) Построить биссектрисы углов треугольника
(на рисунке красным цветом)
2) Биссектрисы будут пересекаться в одной точке.
Она и будет центром окружности

4.

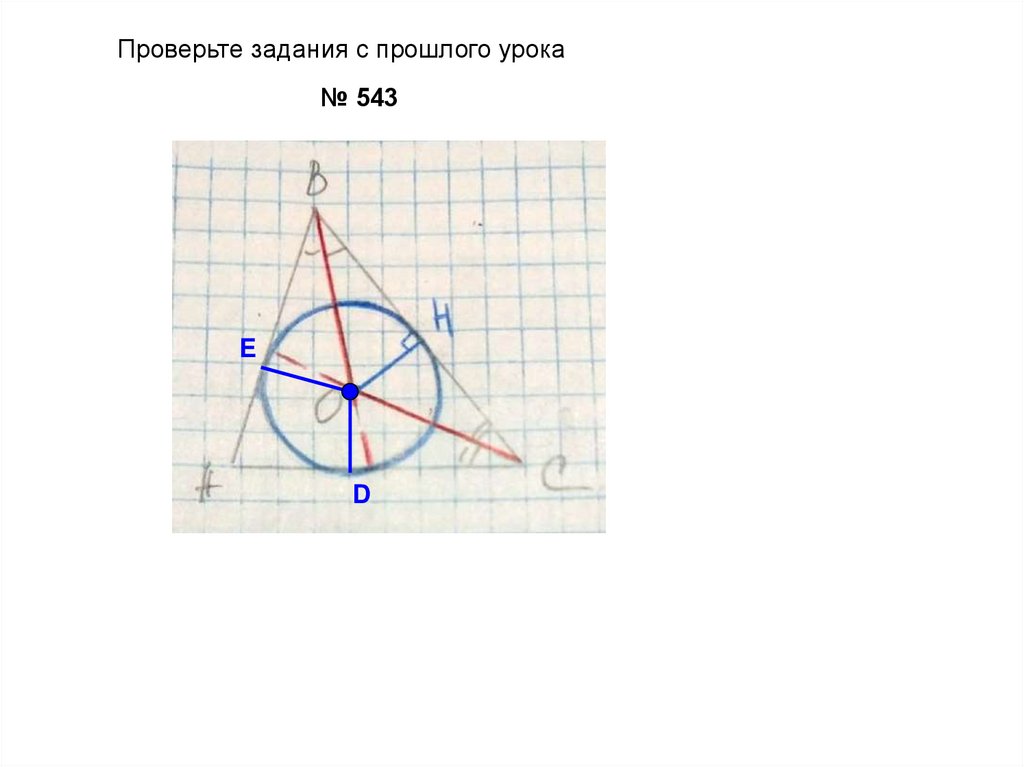
Проверьте задания с прошлого урока
№ 543
E
D

5.

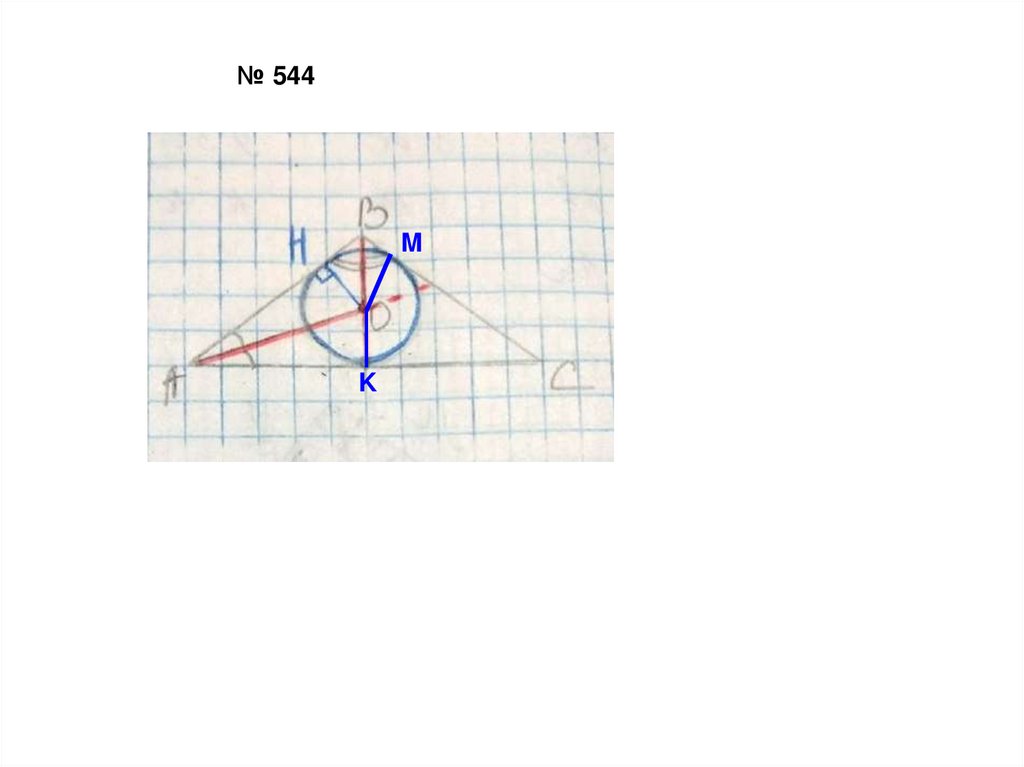
№ 544
M
K

6.

№ 553
Дано: (записать самостоятельно)
О
Решение (план)
1)
2)
3)
4)
5)
Дополнительное построение: радиусы, биссектрисы
Доказать, что треугольник АОМ равен треугольнику АОЕ, тогда АМ = АЕ
Доказать, что треугольник ВМО равен треугольнику ВОК, тогда МВ = ВК
Использовать определение периметра найти ЕС
Найти АС

7.

№ 552
Дано: (записать самостоятельно)
О
Решение (план)
1)
2)
3)
4)
5)
6)
Дополнительное построение: радиусы, биссектрисы
Доказать, что треугольник АОМ равен треугольнику АОЕ, тогда АМ = АЕ
Доказать, что треугольник ВМО равен треугольнику ВОК, тогда МВ = ВК
Доказать, что треугольник СЕО равен треугольнику СКО, тогда ЕС = КС
Найти стороны треугольника АВС
Найти периметр