Практическое занятие 8. Постоянный ток и его законы. Переменный ток. Импеданс цепи переменного тока. Импульсные токи

1.

Практическое занятие 8
Постоянный ток и его законы.
Переменный ток.
Импеданс цепи переменного тока.
Импульсные токи.
1

2.

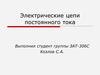
Внешний
источник
U = φ1 - φ 2
φ1
φ2
I
R
Элемент электрической
цепи – резистор,
«подчиняется» закону Ома.
Обладает свойствами
проводников.
U Причина
Следствие I =
R Свойство
2

3.

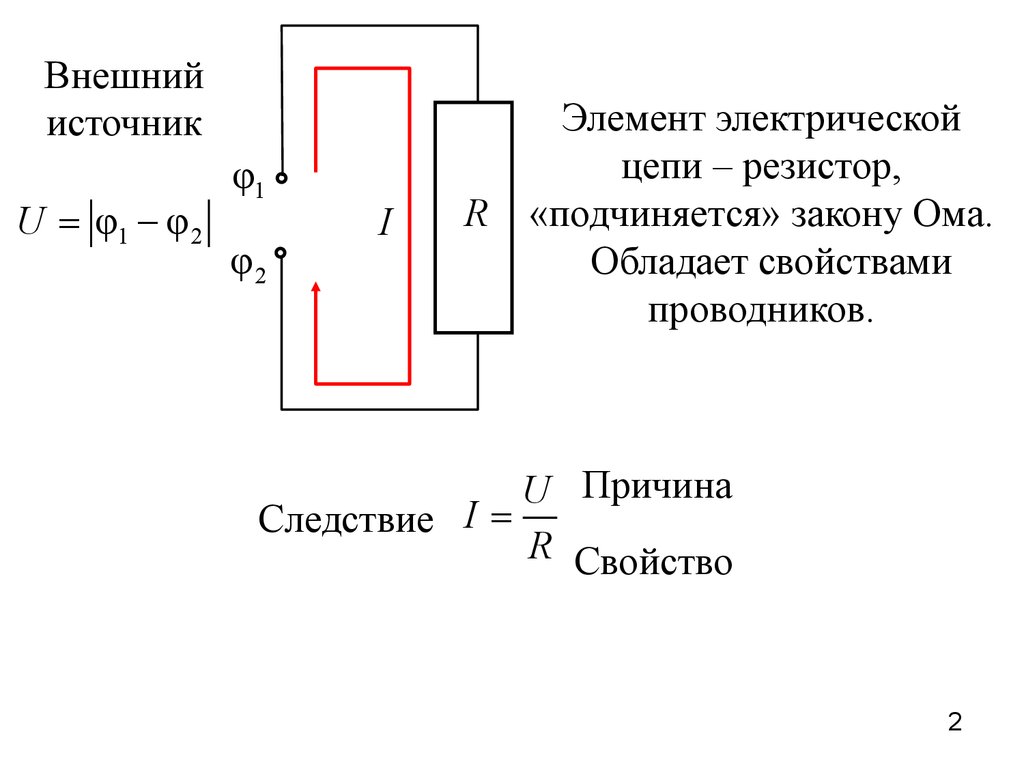
U = φ1 - φ 2 = const
I = const
Цепь постоянного тока
Схемы соединения резисторов:
Последовательная:
R1
R2
I
Параллельная:
I1
R1
I = I1 + I 2
R2 I 2
U = U1 + U 2
U = U1 = U 2
IR = IR1 + IR2
R = R1 + R2
U U U
= +
R R1 R2
1 1
1
= +
R R1 R2
3

4.

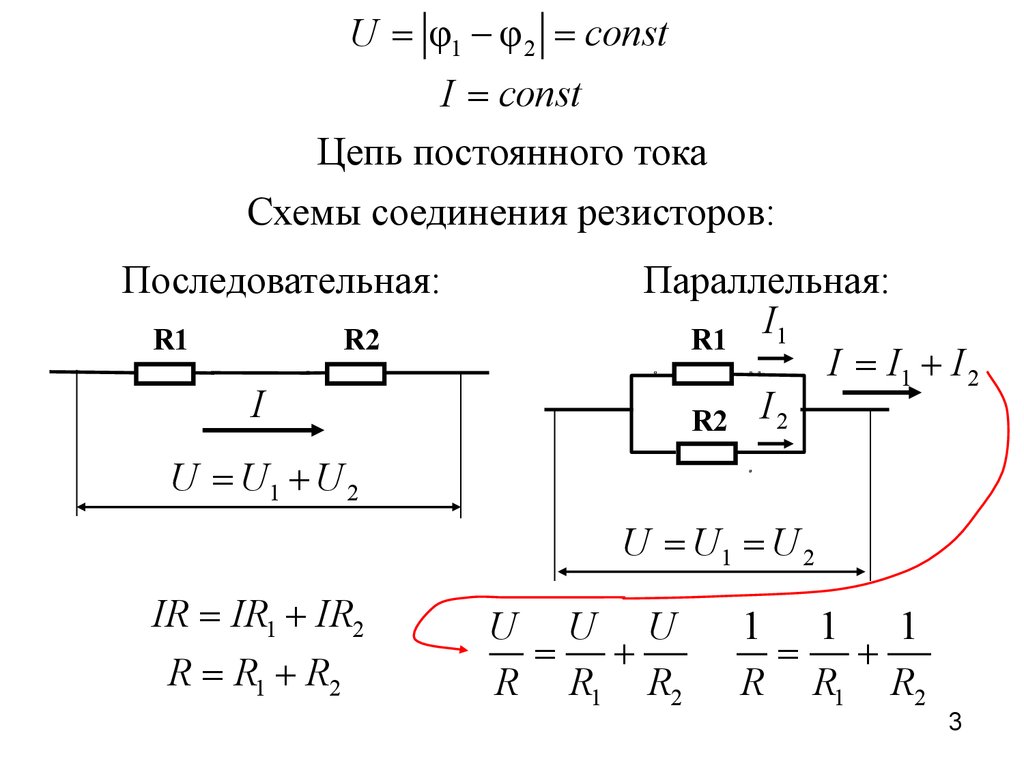
Определить электрическое сопротивление участка
цепи, содержащего резисторы R1 = 5 Ом; R2 = 10 Ом;
R3 = 30 Ом; R4 = 20 Ом; R5 = 10 Ом.
R2
R4
R1
R5
R3
R = R1 + éë( R 2 + R 4 ) P R3ùû + R5
4

5.

R = R1 + éë( R 2 + R 4 ) P R3ùû + R5
R2+ 4 = R 2 + R 4 =
1
R2+3+ 4
1
1
=
+
=
R2+ 4 R3
R2+3+ 4 =
R = R1 + R2+3+ 4 + R5 =
5

6.

Определить токи через все резисторы
цепи, подключенной к источнику напряжения
U = 120 B: R1 = 5 Ом; R2 = 10 Ом;
R3 = 30 Ом; R4 = 20 Ом; R5 = 10 Ом.
R2
R4
R1
R5
R3
6

7.

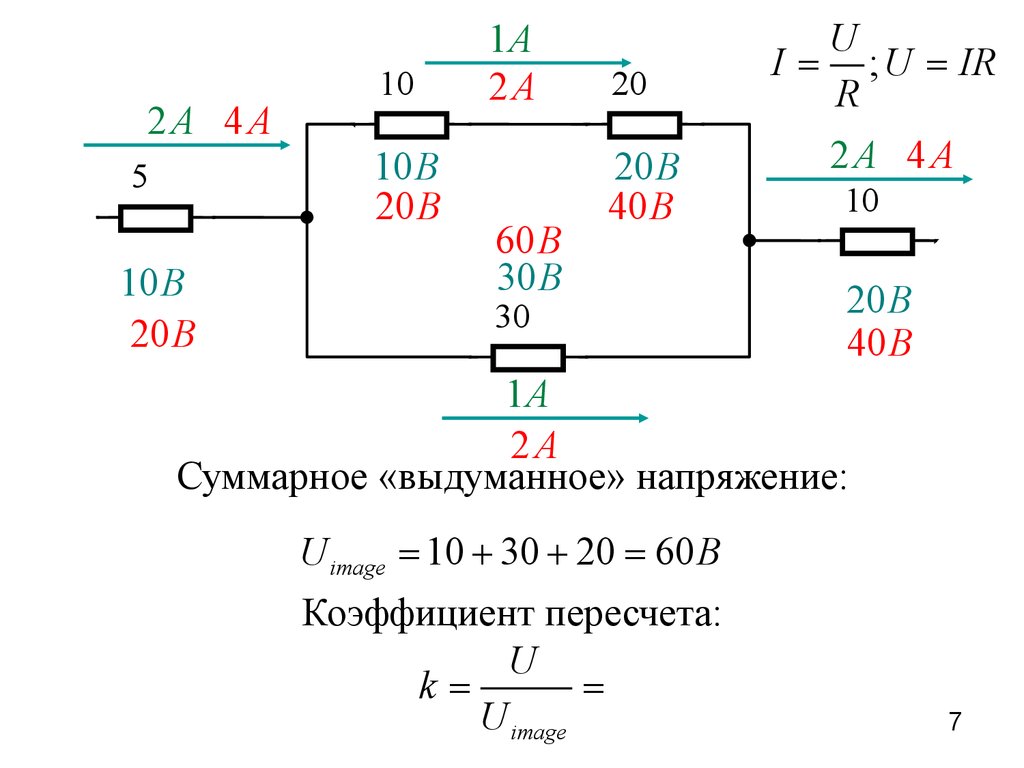
2A 4A
10
10B
20B
5
10B
20B
1A
2A
60B
30B
20
20B
40B
30
U
I = ; U = IR
R
2A 4A
10
20B
40B
1A
2A
Суммарное «выдуманное» напряжение:
U image = 10 + 30 + 20 = 60 B
Коэффициент пересчета:
U
k=
=
U image
7

8.

При сухой коже сопротивление между ладонями рук может
достигать значения R1 = 105 Ом, а при потных (влажных)
ладонях сопротивление будет существенно меньше:
R2 = 1500 Ом. Найти токи, которые возникнут при
контакте с бытовой электросетью с напряжением 220 В.
Оценить опасность воздействия током
(относительно безопасным является ток силой менее 10 мА).
U
I1 =
=
R1
U
I2 =
=
R2
8

9.

При согласовании источника электрической энергии с
нагрузкой в нагрузку от источника передается
максимальная электрическая энергия. Определить
сопротивление нагрузки для согласования источника
постоянного напряжения с внутренним
сопротивлением r = 10 Ом с нагрузкой.
9

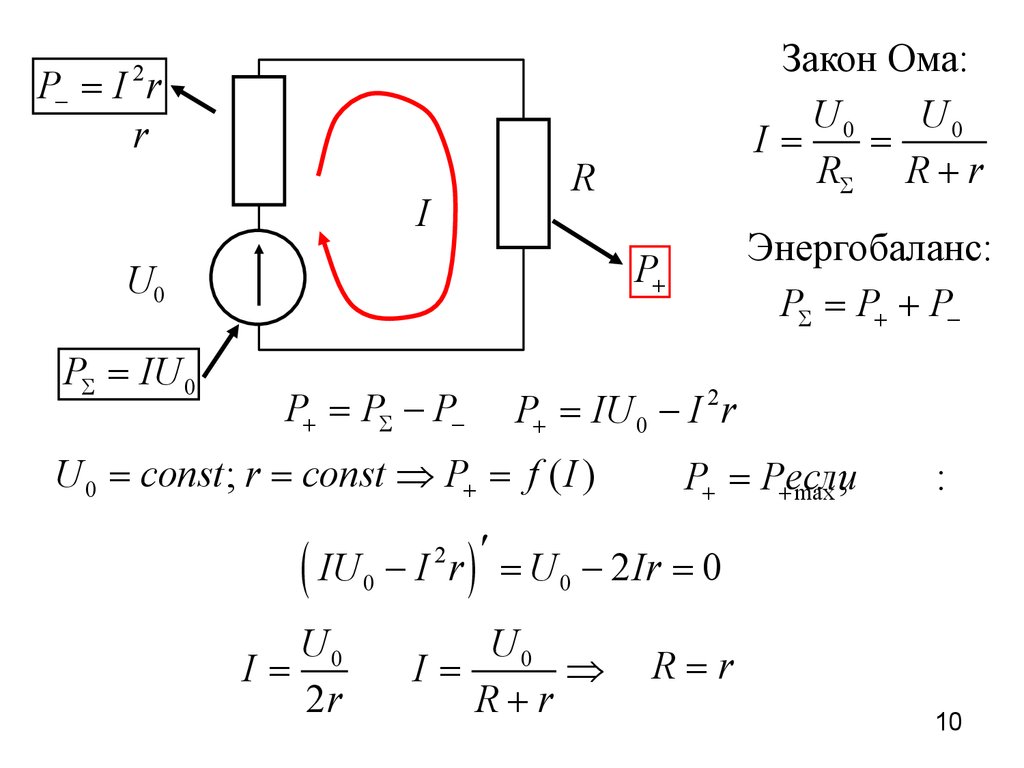
10.

P- = I r
r
Закон Ома:
U0
U0
I=
=
RS R + r
2
R
I
P+
U0
PS = IU 0
Энергобаланс:
PS = P+ + P-
P+ = PS - P-
P+ = IU 0 - I 2 r
U 0 = const ; r = const Þ P+ = f ( I )
P+ = Pесли
+ max ,
:
¢
( IU 0 - I r ) = U 0 - 2Ir = 0
2
U0
I=
2r
U0
I=
Þ
R+r
R=r
10

11.

онденсатор емкостью С разряжается через резистор
сопротивлением R так, что заряд конденсатора
изменяется во времени по закону:
q(t ) = q0e
-
t
RC
-
t
RC
= CUeмкКл
,
Определить закон изменения тока.
11

12.

1
U
C
U = const ; C = const ; R = const
1: q0 = CU
i
=
i
(
t
)
2
2 : q ¯ Þ q = q (t )
R
t
t
q (t ) = q0e RC = CUe RC
dq
i=
= q&
dt
qö
æ
çI = ÷
tø
è
æ - RCt ö æ 1 ö
i = CU ç e ÷ ç ÷
è
ø è RC ø
U æ - RCt ö
i = - çe ÷
Rè
ø
(-) – ?
12

13.

Скорость изменения пороговой силы тока выражается
dI
1,12
соотношением:
= - 2 , мА / с
dt
t
Установить закон изменения силы тока, если в момент времени
t = 0,с4 соответствующее значение силы тока равно 3,2 мА.
Изменение порогового тока за время dt
Разделение переменных:
dt
dI = -1,12 2
t
dt
ò dI = -1,12ò t 2
13

14.

dt
-2
dI
=
I
dI
=
1,12
=
1,12
t
ò
ò
ò t2
ò dt
0
1,12
I=
+C
t
1,12
C = 3,2 =
0,4
Таблица интегралов элементарных функций
f (t )
0
t n , n ¹ -1
e
t
F (t )
A
1 n+1
t
n +1
et
f (t )
cost
F (t )
sin t
sin t
- cost
1
t
ln t
14

15.

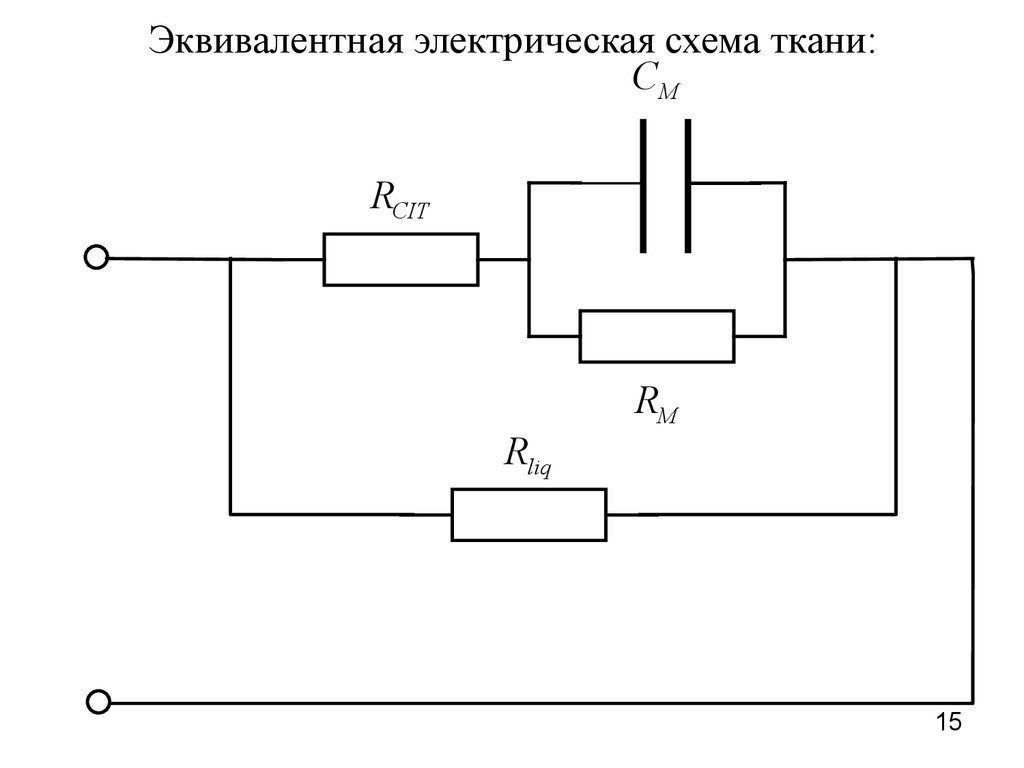
Эквивалентная электрическая схема ткани:
CM
RCIT
RM
Rliq
15

16.

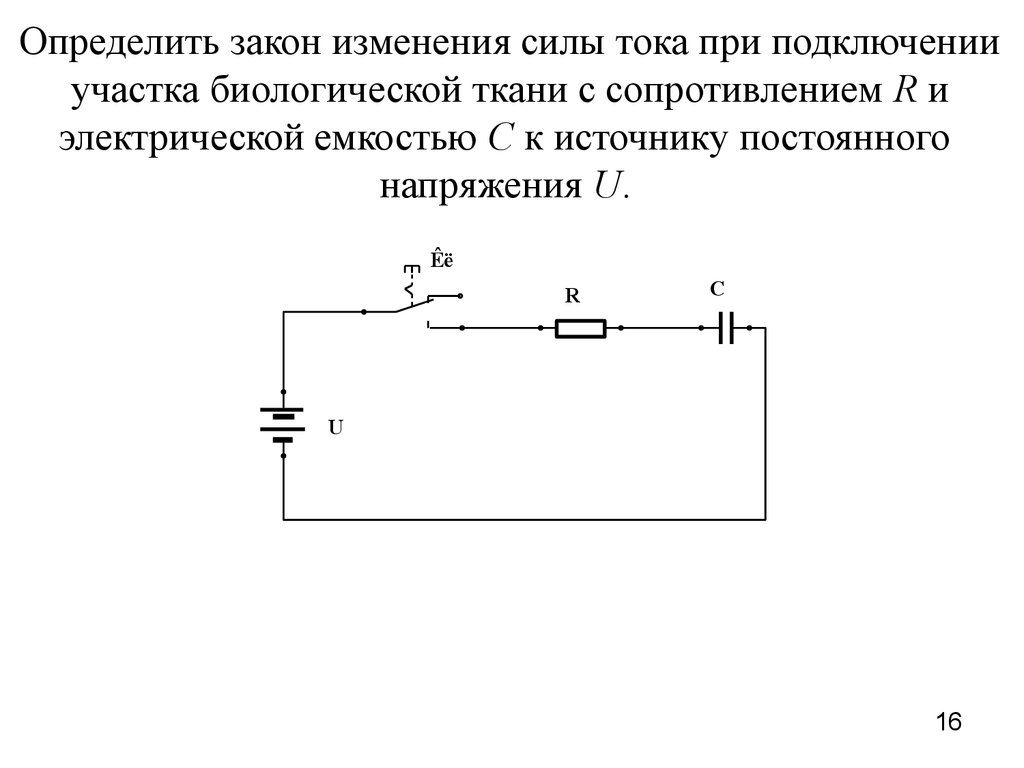
Определить закон изменения силы тока при подключении
участка биологической ткани с сопротивлением R и
электрической емкостью С к источнику постоянного
напряжения U.
Êë
R
C
U
16

17.

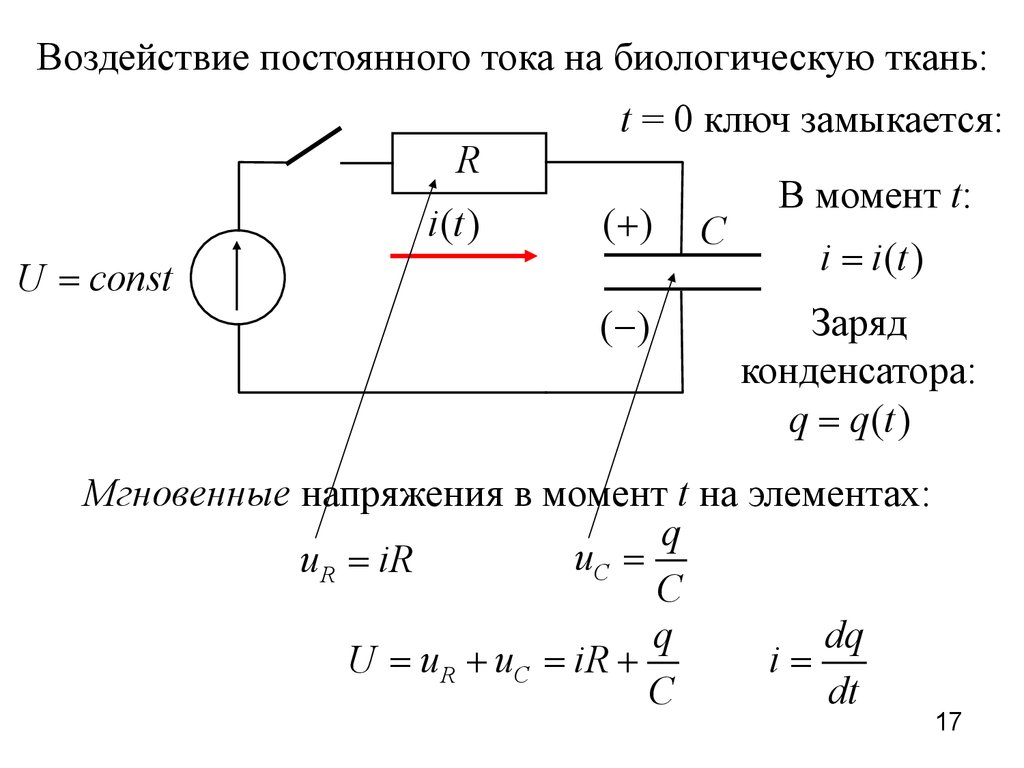
Воздействие постоянного тока на биологическую ткань:
R
i (t )
U = const
t = 0 ключ замыкается:
(+)
( -)
C
В момент t:
i = i (t )
Заряд
конденсатора:
q = q (t )
Мгновенные напряжения в момент t на элементах:
q
uC =
u R = iR
C
q
dq
U = u R + uC = iR +
i=
C
dt
17

18.

Дифференциальное уравнение, описывающее
поведение конкретной системы:
dq 1
U =R + q
dt C
dq
CU = RC
+q
dt
CU = q0 = q (t ® ¥)
dq
q0 - q = RC
dt
Разделение переменных и дифференциалов –
переменные к «своим» дифференциалам,
все постоянные в «общую кучу»:
dt
dq
=
RC q0 - q
18

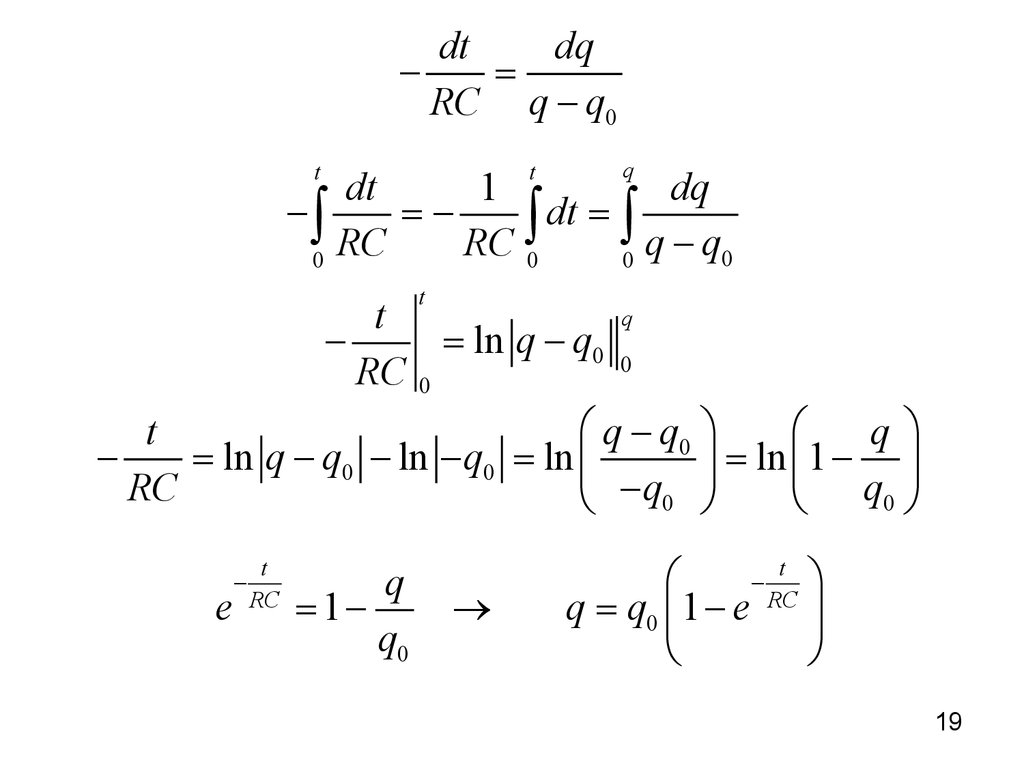
19.

dt
dq
=
RC q - q0
t
t
q
dt
1
dq
-ò
=dt = ò
ò
RC
RC 0
q - q0
0
0
t
q
t
= ln q - q0 0
RC 0
æ q - q0 ö
æ
t
qö
= ln q - q0 - ln - q0 = ln ç
÷ = ln ç1 - ÷
RC
è -q0 ø
è q0 ø
e
-
t
RC
q
= 1q0
®
t
æ
ö
RC
q = q0 ç1 - e ÷
è
ø
19

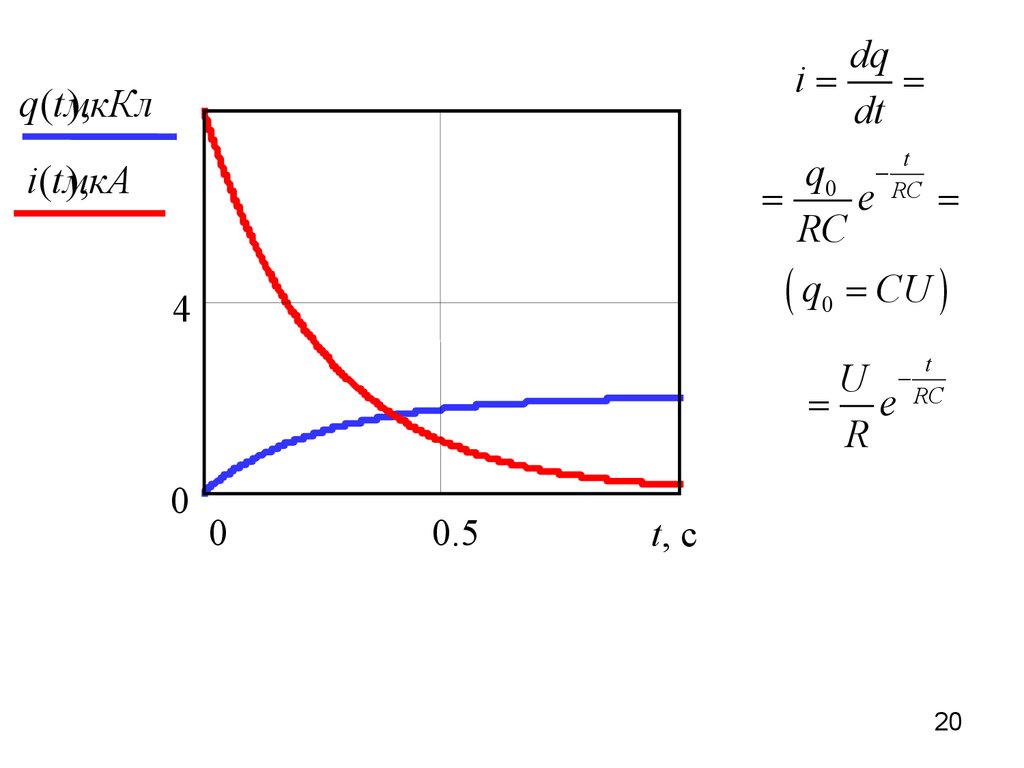
20.

dq
i=
=
dt
q (tмкКл
),
q0 - RCt
=
e
=
RC
i (tмкА
),
( q0 = CU )
4
U - RCt
= e
R
0
0
0.5
t, с
20

21.

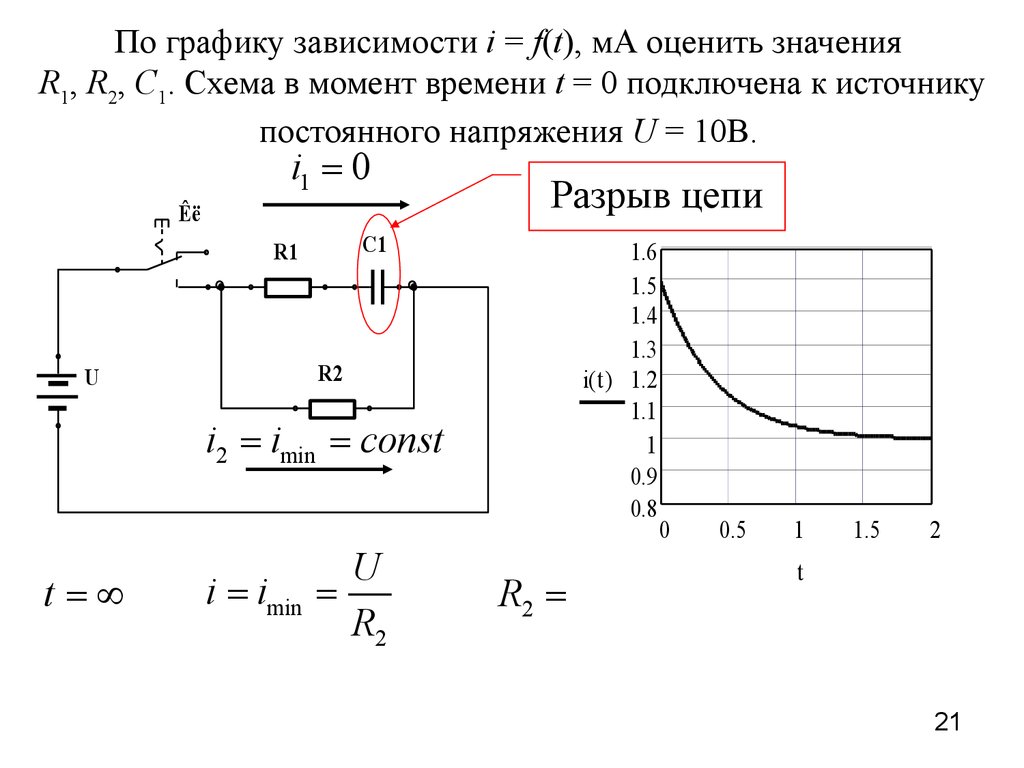
По графику зависимости i = f(t), мА оценить значения
R1, R2, C1. Схема в момент времени t = 0 подключена к источнику
постоянного напряжения U = 10В.
i1 = 0
Êë
Разрыв цепи
C1
R1
1.6
1.5
1.4
1.3
i( t ) 1.2
1.1
1
0.9
0.8
R2
U
i2 = imin = const
t=¥
i = imin
U
=
R2
R2 =
0
0.5
1
1.5
2
t
21

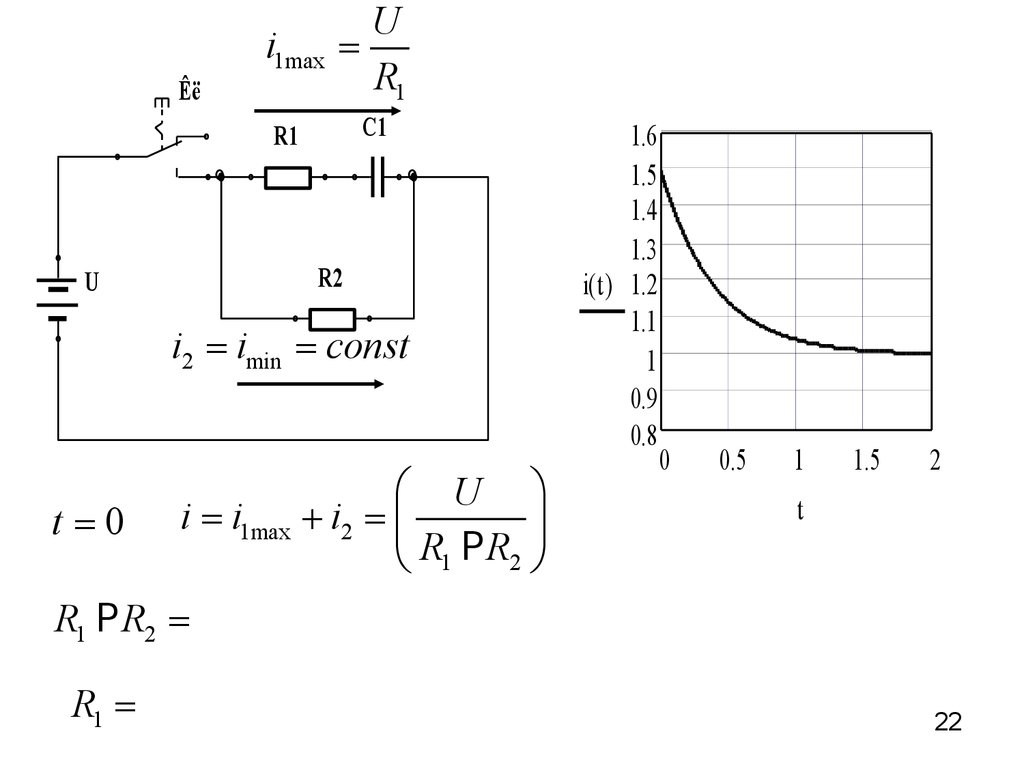
22.

i1max
Êë
U
=
R1
C1
R1
R2
U
i2 = imin = const
t=0
æ U ö
i = i1max + i2 = ç
÷
è R1 P R2 ø
1.6
1.5
1.4
1.3
i( t ) 1.2
1.1
1
0.9
0.8
0
0.5
1
1.5
2
t
R1 P R2 =
R1 =
22

23.

Êë
Электромагнитный контур
q – заряд конденсатора в момент времени t ;
u – напряжение на конденсаторе в момент t
+
Ñ
q
uC =
C
i
q
&+ = 0
Lq&
C
Сила тока в контуре в момент t:
dq
i=
= var
dt
di
L
&
i = varεÞ i = - L = - Li¢ = - Lq&
dt
Закон сохранения энергии:
uC = ε i
q
di
&
uC = = e i = - L = - Lq&
C
dt
1
&+
q&
q=0 Û &
x&+ ω02 × x = 0
LC
23

24.

Вывод:
1
&+
q&
q=0
LC
1. q = q0 cos(ω0t + φ 0 )
2.ω
0
=
1
LC
2π
T=
= 2π LC
ω0
24

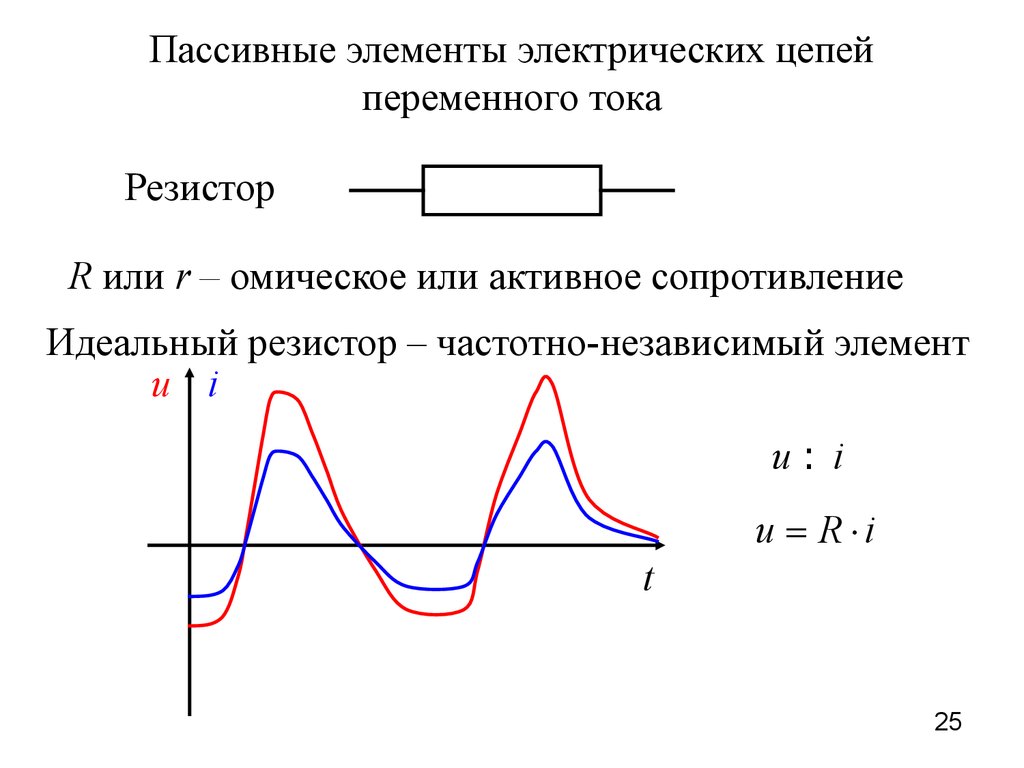
25.

Пассивные элементы электрических цепей
переменного тока
Резистор
R или r – омическое или активное сопротивление
Идеальный резистор – частотно-независимый элемент
u i
u: i
u = R ×i
t
25

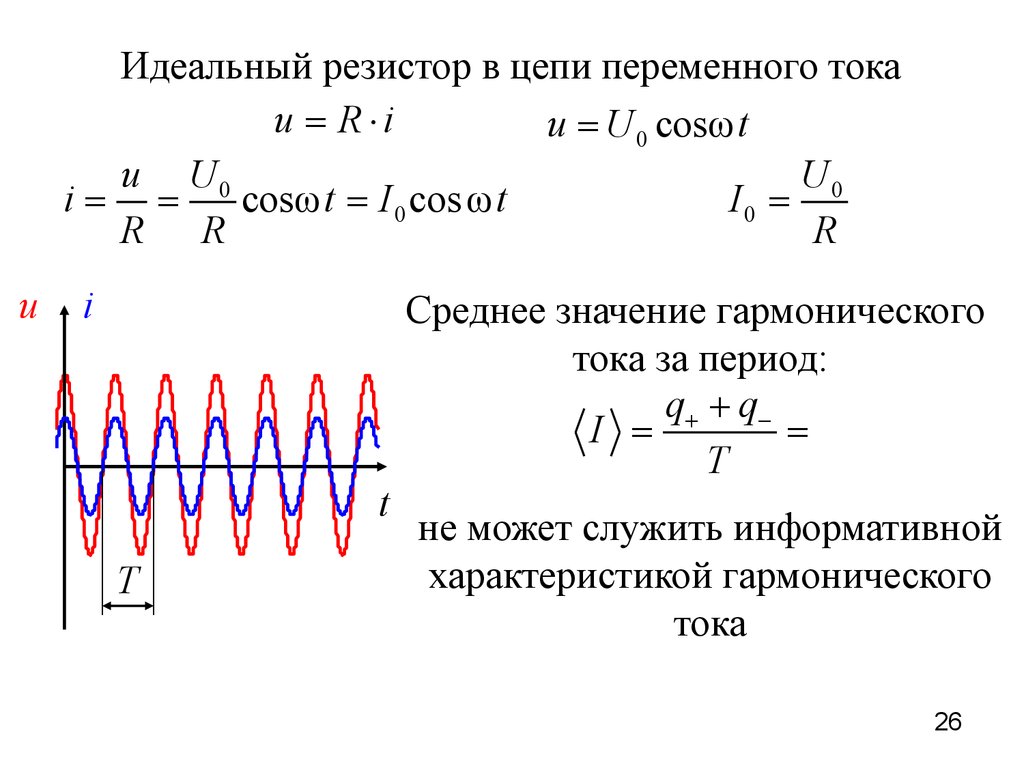
26.

Идеальный резистор в цепи переменного тока
u = R ×i
u = U 0 cosω t
u U0
U0
i= =
cosω t = I 0 cosω t
I0 =
R R
R
u
i
t
T
Среднее значение гармонического
тока за период:
q+ + qI =
=
T
не может служить информативной
характеристикой гармонического
тока
26

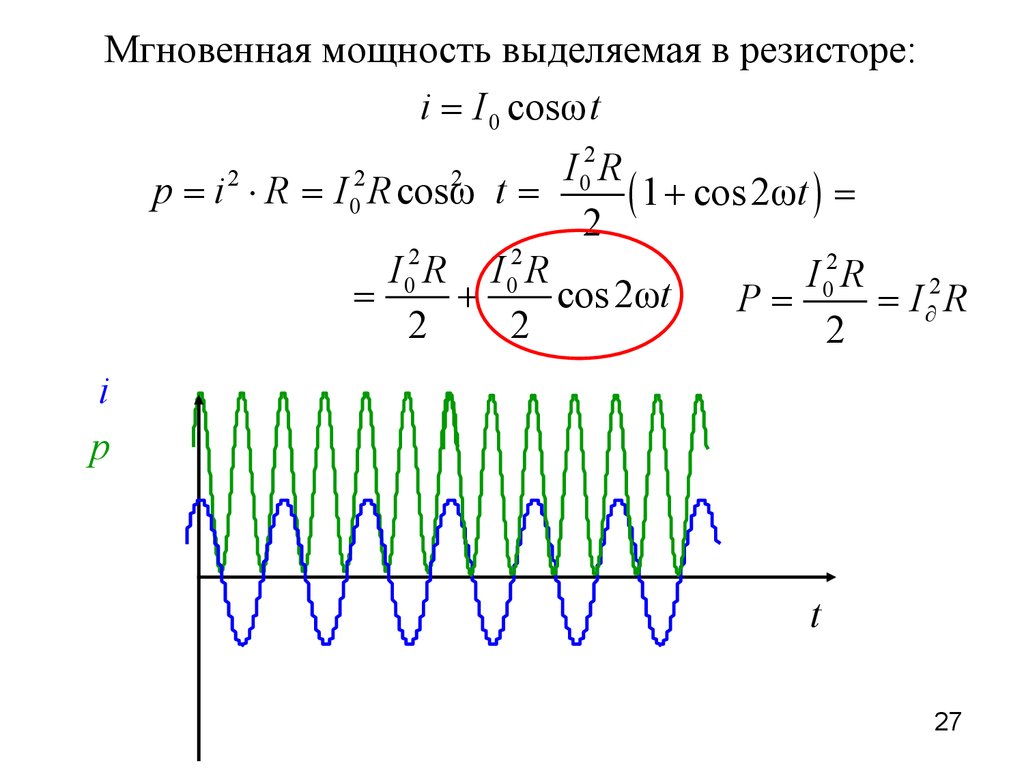
27.

Мгновенная мощность выделяемая в резисторе:
i = I 0 cosω t
2
I
2
2
2
0R
p = i × R = I 0 R cosω t =
( 1 + cos 2ωt ) =
2
I 02 R I 02 R
I 02 R
=
+
cos 2ωt
P=
= I ¶2 R
2
2
2
i
p
t
27

28.

Действующие значения тока и напряжения
I0
U0
I¶ = I =
U¶ = U =
2
2
Только для резистора закон Ома:
u U0 U
R= =
=
i
I0
I
Мощность, выделяемая в резисторе - активная:
I 02 R
P=
= I 2R
2
R или r – омическое или активное сопротивление
28

29.

Конденсатор в цепи переменного тока:
q
Электрическая емкость конденсатора: C = = const
U
С
Мгновенный заряд конденсатора:
q = Cu = CU 0 cosω t = q0 cosω t q0 = CU 0
Мгновенный ток через конденсатор:
u = U 0 cosω t
dq
i=
= -ωC × U 0 sin ωt =
dt
πö
πö
æ
æ
I 0 = ωC × U 0
= ωC × U 0 cos ç ωt + ÷ = I 0 cosω
ç t+ ÷
2ø
2ø
è
è
29

30.

u = U 0 cosω t
u
i
i = - I 0 sinω t
πö
æ
i = ωC × U 0 cos ç ωt + ÷
2ø
è
t
30

31.

Выводы:
1. Колебания тока в данной цепи «опережают» колебания
напряжения на π/2 (90º).
2. Конденсатор «ведет себя» не так, как резистор.
Поэтому и суммарная цепь переменного тока «ведет»
себя отличительно от цепи постоянного тока:
для цепи постоянного тока идеальный конденсатор –
разрыв цепи
Для цепи переменного тока с конденсатором:
U0
1
=
I 0 = ωC × U 0 Þ xC =
I 0 ωC
Формальный
закон Ома
31

32.

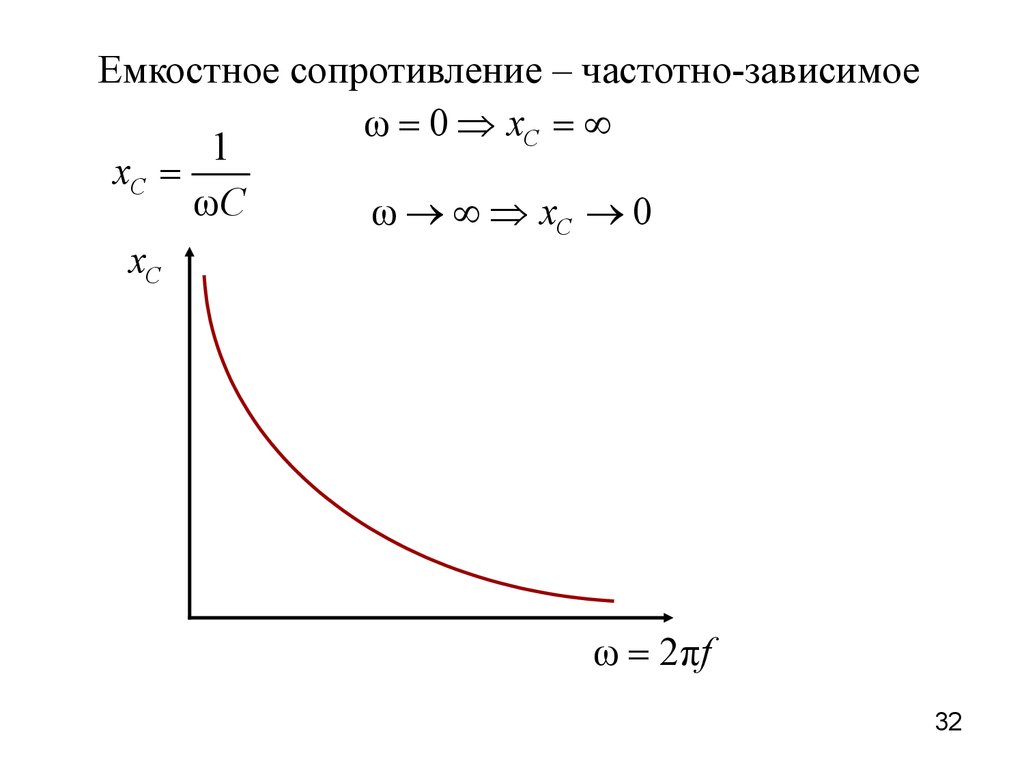
Емкостное сопротивление – частотно-зависимое
ω = 0 Þ xC = ¥
1
xC =
ωC
ω ® ¥ Þ xC ® 0
xC
ω = 2πf
32

33.

Эквивалентная схема замещения цепи, содержащей
резистивные и емкостные элементы:
C
u (t ) = U 0 cosω t
R
i (t ) = I 0 cosω
( t +φ )
u (t )
i (t )
φ – суммарный сдвиг колебаний
тока относительно колебаний
напряжения в в цепи
Полное сопротивление (импеданс) подобной цепи:
U0
æ 1 ö
2
2
2
z=
= R + xC = R + ç
÷
I0
ω
C
è
ø
2
33

34.

Найти полное сопротивление переменному току, если
последовательно включены резистор сопротивлением
R = 6 Ом и конденсатор с емкостным сопротивлением
хC = 8 Ом.
z= R +x =
2
2
C
Найти полное сопротивление переменному току
частотой 50 Гц, если последовательно включены
резистор сопротивлением R = 6 Ом и конденсатор
с емкостью С = 10 мкФ =
2
æ
ö
1
z = R +ç
=
÷
è 2π × f × C ø
2
34

35.

Определить характеристики импульсного сигнала:
амплитуду, период следования импульсов,
длительность импульса, скважность, коэффициент
заполнения, крутизну переднего фронта.
T
Q= =
I max =
τi =
T=
i, мА
τi
0,4
1τ i
k= = =
0,3
Q T
di
Di
0,2
K R PF =
=
=
dt PF Dt
0,1
0
0,5
1
t, мс
35