Похожие презентации:
Задачи классификации и регрессии. Технологии обработки данных
1. Задачи классификации и регрессии
2. Технологии обработки данных
• Knowledge Discovery in Databases(KDD) – процесс получения из данных
знаний в виде зависимостей, правил,
моделей.
• Data Mining (DM) – обнаружение в
данных неизвестных нетривиальных
знаний, необходимых для принятия
решений.
3. Методы DM
• Классификация – установление зависимостидискретной выходной переменной от входных.
• Кластеризация – группировка объектов на основе
свойств.
• Регрессия - установление зависимости непрерывной
выходной переменной от входных.
• Ассоциация – выявление закономерностей между
связанными событиями.
• Последовательные шаблоны – установление
закономерностей между связанными во времени
событиями
4. Решение задач классификации
Логистическая регрессия
Метод опорных векторов
Деревья решений
Байесовские алгоритмы
5.
Задача классификации данныхЗадача классификации формулируется следующим образом.
Имеется множество объектов
X x , h 1, H
h
аждый объект характеризуется набором свойств x1 ,..., x n
и меткой принадлежности к классу q
из множества классов q Q
при известном наборе характеристик x
некоторый объект необходимо отнести к какому-либо классуq Q
Свойства объекта могут быть булевыми, дискретными или
непрерывными, а метку класса обычно представляют в виде
номера класса, то есть дискретной переменной.
6.
Метод опорных векторовРассмотрим задачу бинарной классификации.
Имеющийся набор данных
X {x , q }, h 1, H
h
h
содержит два класса q { 1; 1}
Требуется построить поверхность, разделяющую все
множество точек на два подмножества
q 1
и q 1
Сначала предположим возможность линейного разделения, то
есть, поверхность представляет собой разделительную
гиперплоскость.
7.
Уравнение разделительной гиперплоскости в пространствепеременных
x Rn
представим в виде n
T
w
x
b
w
x b 0
j j
j 1
а линейный пороговый классификаторq SL ( x)
Коэффициенты
w j , j 1, n; b
подбираются в процессе обучения.
sign w x b
T
8.
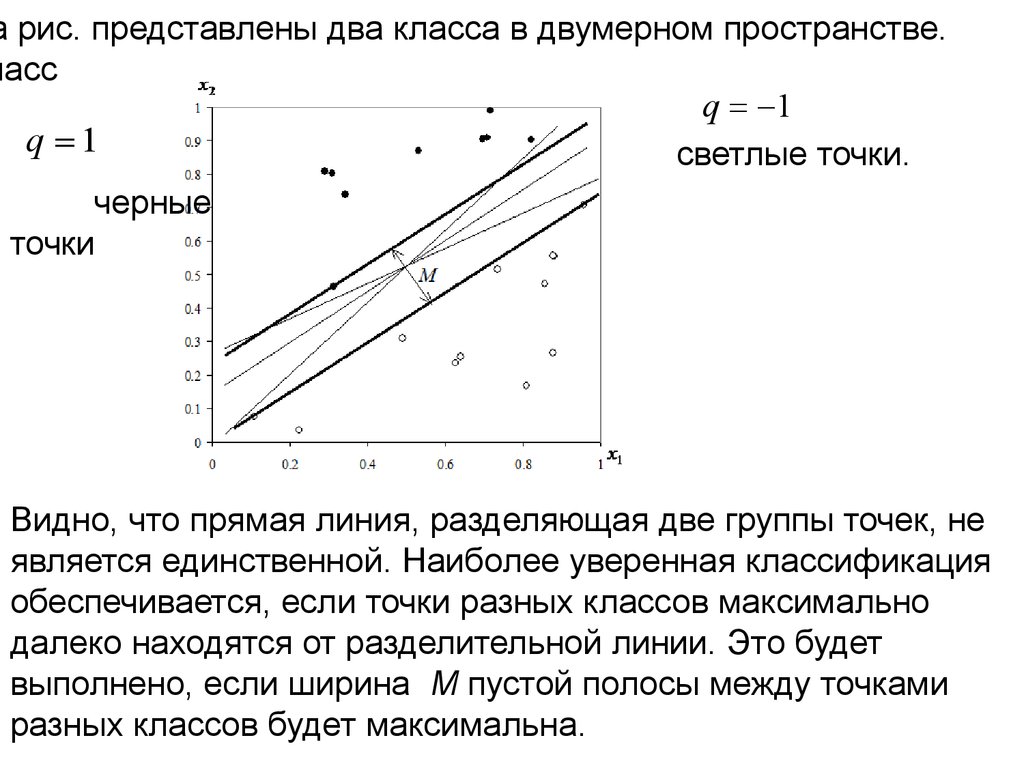
а рис. представлены два класса в двумерном пространстве.ласс
q 1
q 1
светлые точки.
черные
точки
Видно, что прямая линия, разделяющая две группы точек, не
является единственной. Наиболее уверенная классификация
обеспечивается, если точки разных классов максимально
далеко находятся от разделительной линии. Это будет
выполнено, если ширина М пустой полосы между точками
разных классов будет максимальна.
9.
Коэффициентыwj ,b
можно пронормировать таким
T
образом, чтобы
w x b q
в точках, ближайших к разделяющей классы полосе. В
остальных точках условие
1 |q 1
T
w x b
1 | q 1
выполняется с запасом. Ширина полосы М рассчитывается
как расстояние между двумя параллельными плоскостями
w x b 1 и w x b 1 M
T:
T
(b 1) (b 1)
T
w w
2
wT w
Следовательно, максимум М соответствует
0.5wT w min
и получим задачу оптимизации с ограничениями
q h ( wT x h b) 1, h 1, H
10.
11.
Если в данных присутствует существенная нелинейность,то решение задачи не приводит к правильной классификации.
На рисунке приведены данные такого типа.
12.
Выражение дляклассификатора
H
SVM
h
h
q (x) sign h q K (x , x) b
h 1
Практически
ядра:
используются следующие функции
K (x, x ) x T x
K (x, x ) x x 1
T
d
K (x, x ) exp 0.5(x x ) T 1 (x x )
K (x, x ) tanh x T x w0
K (x, x )
.
1
2
x x
x T x
13.
Для примера на рис. представлена выборка из 190 точек.Нелинейное разделение с
радиальным ядром
Опорные вектора
отмечены крестиками.
Эти точки расположены
на разделяющей классы
замкнутой поверхности.
Неправильно
классифицированные
точки обведены
квадратиками. Таких
точек три из 190.
Треугольниками
обозначены точки из
проверочной выборки,
не участвующие в
обучении.
14.
Байесовские классификаторы15.
16.
17.
18.
19.
20.
21.
22.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
2
1
1
1
1
2
1
1
2
1
2
1
4
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
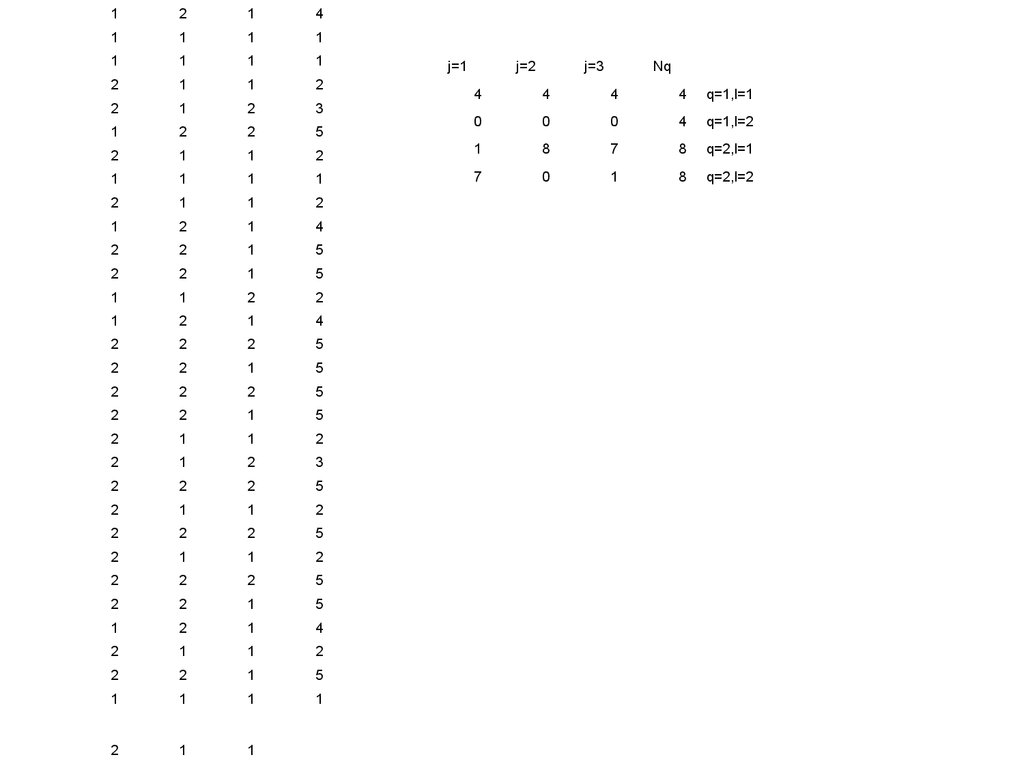
Последовательность действий
H hjq
j=1
j=2
4
j=3
4
Nq
4
4
q=1,l=1
23.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
2
1
1
1
1
2
1
1
2
1
2
1
4
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
24.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
2
1
1
1
1
2
1
1
2
1
2
1
4
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
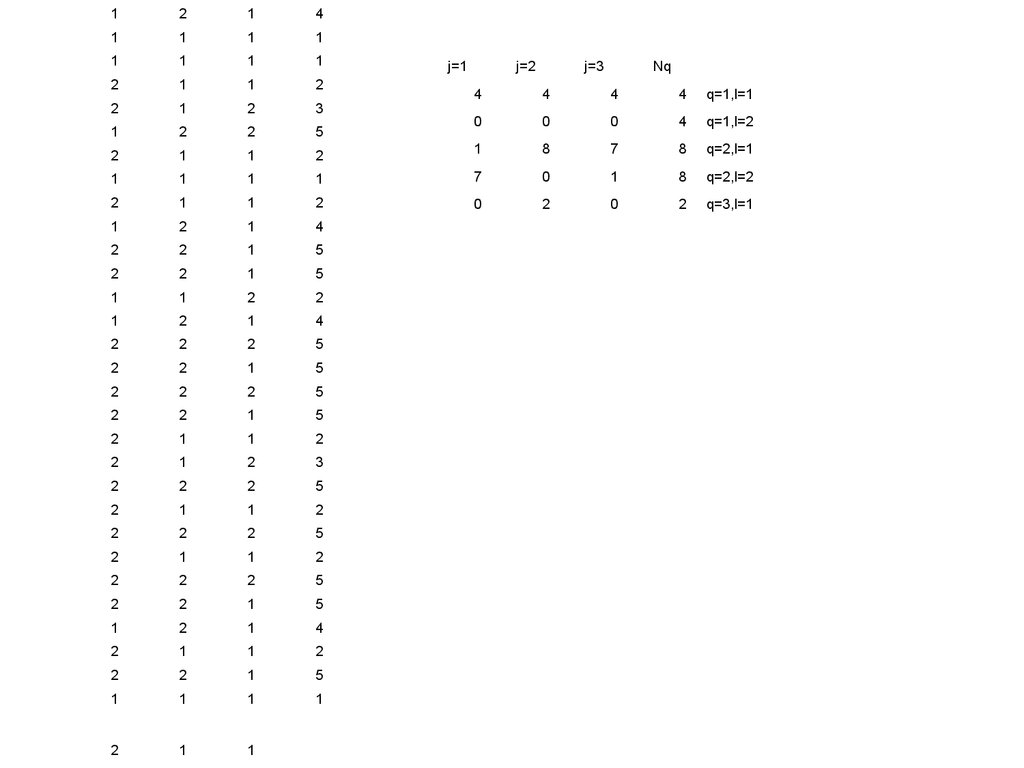
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
1
8
7
8
q=2,l=1
25.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
1
2
1
4
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
26.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
27.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
0
2
2
q=3,l=2
2
2
1
5
2
2
1
5
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
28.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
0
2
2
q=3,l=2
2
2
1
5
2
2
1
5
4
0
4
4
q=4,l=1
1
1
2
2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
29.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
0
2
2
q=3,l=2
2
2
1
5
2
2
1
5
4
0
4
4
q=4,l=1
1
1
2
2
0
4
0
4
q=4,l=2
1
2
1
4
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
30.
12
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
0
2
2
q=3,l=2
2
2
1
5
2
2
1
5
4
0
4
4
q=4,l=1
1
1
2
2
0
4
0
4
q=4,l=2
1
2
1
4
1
0
6
12
q=5,l=1
2
2
2
5
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
5
2
1
1
2
2
2
2
5
2
2
1
5
1
2
1
4
2
1
1
2
2
2
1
5
1
1
1
1
2
1
1
31.
,1
2
1
4
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
3
1
2
2
5
2
1
1
1
1
2
j=1
j=2
j=3
Nq
4
4
4
4
q=1,l=1
0
0
0
4
q=1,l=2
2
1
8
7
8
q=2,l=1
1
1
7
0
1
8
q=2,l=2
1
1
2
0
2
0
2
q=3,l=1
1
2
1
4
2
0
2
2
q=3,l=2
2
2
1
5
2
2
1
5
4
0
4
4
q=4,l=1
1
1
2
2
0
4
0
4
q=4,l=2
1
2
1
4
1
0
6
12
q=5,l=1
2
2
2
5
11
12
6
12
q=5,l=2
2
2
1
5
2
2
2
5
2
2
1
5
2
1
1
2
2
1
2
3
2
2
2
5
2
1
1
2
2
2
2
2
1
2
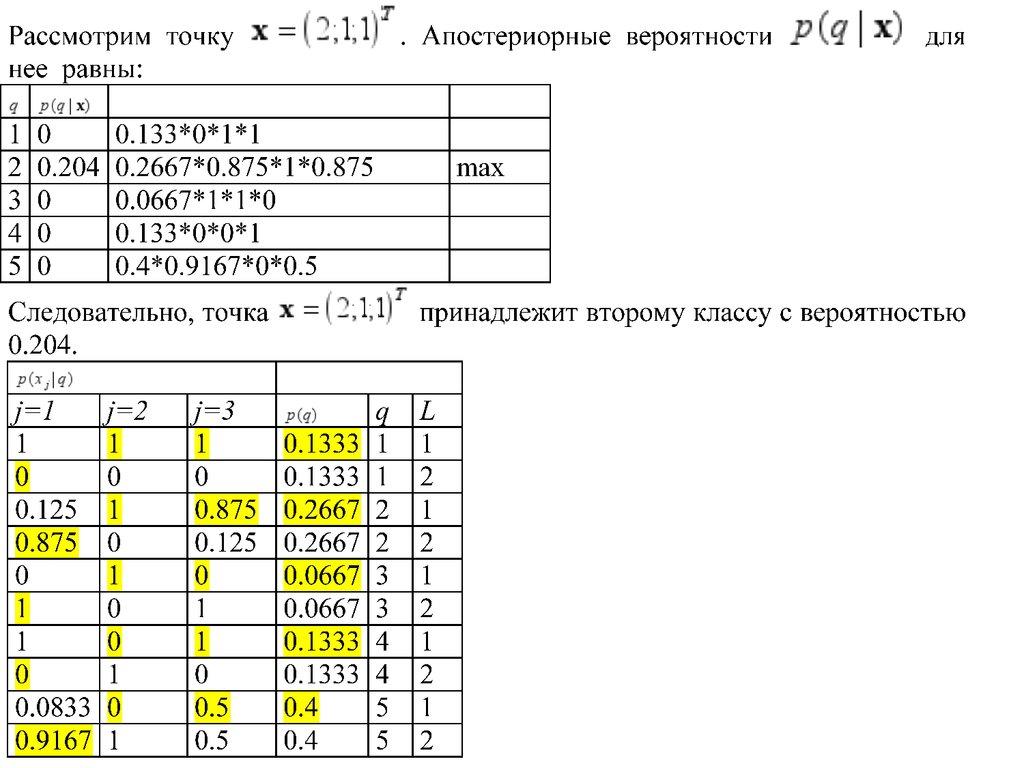
p(q)
j=1
j=2
1
1
0.1333
q=1,l=1
0
0
0
0.1333
q=1,l=2
5
0.125
1
0.875
0.2667
q=2,l=1
1
2
0.875
0
0.125
0.2667
q=2,l=2
2
2
5
0
1
0
0.0667
q=3,l=1
2
2
1
5
1
0
1
0.0667
q=3,l=2
1
2
1
4
2
1
1
2
1
0
1
0.1333
q=4,l=1
2
2
1
5
0
1
0
0.1333
q=4,l=2
1
1
1
1
0.0833
0
0.5
0.4
q=5,l=1
0.9167
1
0.5
0.4
q=5,l=2
1
1
H
j=3
1
2
Hq
p( x j | q)
H qjl
Hq
32.
33.
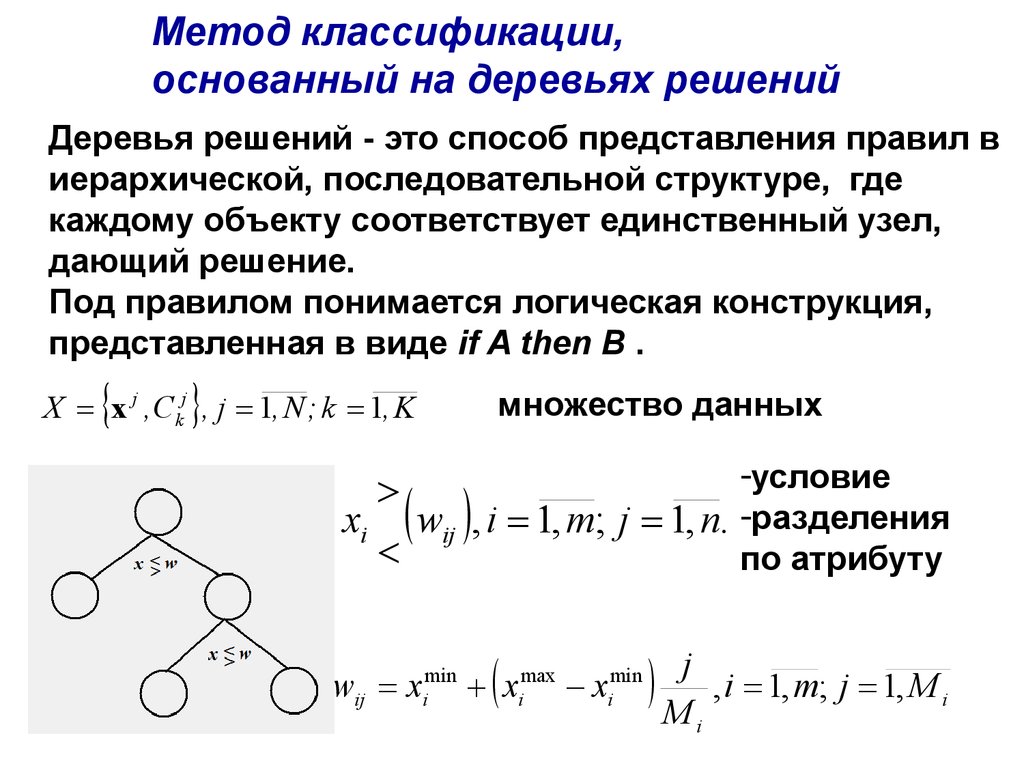
Метод классификации,основанный на деревьях решений
Деревья решений - это способ представления правил в
иерархической, последовательной структуре, где
каждому объекту соответствует единственный узел,
дающий решение.
Под правилом понимается логическая конструкция,
представленная в виде if A then B .
множество данных
X x j ,C kj , j 1, N ; k 1, K
-условие
xi wij , i 1, m; j 1, n. -разделения
по атрибуту
wij x
min
i
x
max
i
x
min
i
j
, i 1, m; j 1, M i
Mi
34.
P , k 1, K ; i 1, m 1; q 1, n; l 1,2k
liq
- вероятность принадлежности
w ,i 1, m 1; j 1, n.
x
классу k по атрибуту i
i
ij
и q-му пороговому значению
k
- вероятность попадания в класс k.
l
P
Разбиению множества X по проверке t соответствует
выражение для энтропии Шеннона
K
H iq P log 2 P
l
k 1
k
liq
Критерий выбора
k
liq
H iq min
35.
0 if X[1] >= 0.36 AND X[0] >= 1.64 then Y= 11 if X[0] >= 0.13 AND X[0] < 1.64 AND X[1] >= 1.60 then Y= 0
2 if X[0] < 1.64 AND X[1] < 1.60 AND X[1] >= 0.61 AND X[0] >= 1.18 then Y= 1
3 if X[1] < 1.60 AND X[1] >= 0.61 AND X[0] >= 1.08 AND X[0] < 1.18 then Y= 0
4 if X[1] < 1.60 AND X[1] >= 0.61 AND X[0] >= 0.64 AND X[0] < 1.08 then Y= 0
5 if X[0] >= 0.13 AND X[1] < 1.60 AND X[1] >= 0.61 AND X[0] < 0.64 then Y= 0
6 if X[1] >= 0.36 AND X[0] < 1.64 AND X[1] < 0.61 AND X[0] >= 0.41 then Y= 1
7 if X[1] >= 0.36 AND X[0] >= 0.13 AND X[1] < 0.61 AND X[0] < 0.41 then Y= 0
8 if X[1] >= 0.36 AND X[0] >= -0.37 AND X[0] < 0.13 then Y= 0
9 if X[1] >= 0.36 AND X[0] >= -1.18 AND X[0] < -0.37 then Y= 0
10 if X[1] >= 0.36 AND X[0] < -1.18 then Y= 0
11 if X[1] < 0.36 AND X[0] >= 0.40 then Y= 1
12 if X[1] < 0.36 AND X[0] < 0.40 AND X[0] >= -1.54 AND X[1] >= -0.01 then Y= 0
13 if X[0] < 0.40 AND X[1] >= -1.50 AND X[1] < -0.01 AND X[0] >= -0.38 then Y= 1
14 if X[0] >= -1.54 AND X[1] < -0.01 AND X[0] < -0.38 AND X[1] >= -0.72 then Y= 0
15 if X[1] >= -1.50 AND X[0] < -0.38 AND X[1] < -0.72 AND X[0] >= -1.22 then Y= 1
16 if X[1] >= -1.50 AND X[0] >= -1.54 AND X[1] < -0.72 AND X[0] < -1.22 then Y= 0
17 if X[1] < 0.36 AND X[1] >= -1.50 AND X[0] < -1.54 then Y= 0
18 if X[0] < 0.40 AND X[1] < -1.50 then Y= 1
36.
0 if X[1] >= 1.39 then Y= 01 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] >= 1.43 then Y= 0
2 if X[1] < 1.39 AND X[0] < 1.43 AND X[1] >= -0.07 AND X[0] >= 1.23 then Y= 0
3 if X[1] < 1.39 AND X[0] >= 0.91 AND X[1] >= -0.07 AND X[0] < 1.23 then Y= 1
4 if X[0] < 1.43 AND X[0] >= 0.91 AND X[1] >= -1.06 AND X[1] < -0.07 then Y= 1
5 if X[1] >= -1.52 AND X[0] < 1.43 AND X[0] >= 0.91 AND X[1] < -1.06 then Y= 0
6 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] >= 0.25 AND X[0] < 0.91 then Y= 1
7 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] >= 0.04 AND X[0] < 0.25 then Y= 1
8 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] >= -0.28 AND X[0] < 0.04 then Y= 1
9 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] >= -0.63 AND X[0] < -0.28 then Y= 1
10 if X[1] < 1.39 AND X[0] < -0.63 AND X[1] >= -1.00 AND X[0] >= -1.01 then Y= 1
11 if X[1] < 1.39 AND X[0] >= -1.47 AND X[0] < -1.01 AND X[1] >= 0.67 then Y= 0
12 if X[0] >= -1.47 AND X[1] >= -1.00 AND X[0] < -1.01 AND X[1] < 0.67 then Y= 1
13 if X[1] >= -1.52 AND X[0] >= -1.47 AND X[0] < -0.63 AND X[1] < -1.00 then Y= 0
14 if X[1] < 1.39 AND X[1] >= -1.52 AND X[0] < -1.47 then Y= 0
15 if X[1] < -1.52 then Y= 0
37.
Разделение областиДерево решений




























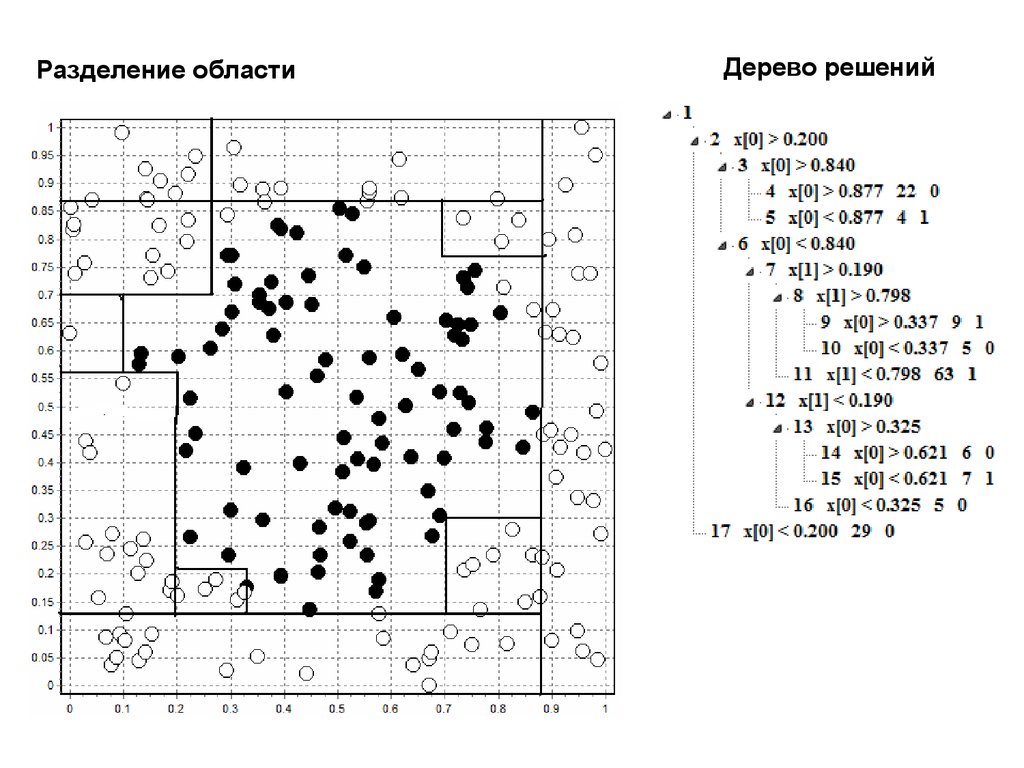
 Информатика
Информатика








