Mongeova projekcia

1. Snímek 1

Vajsáblová, M.: Deskriptívna geometria pre GaK
Margita Vajsáblová
35

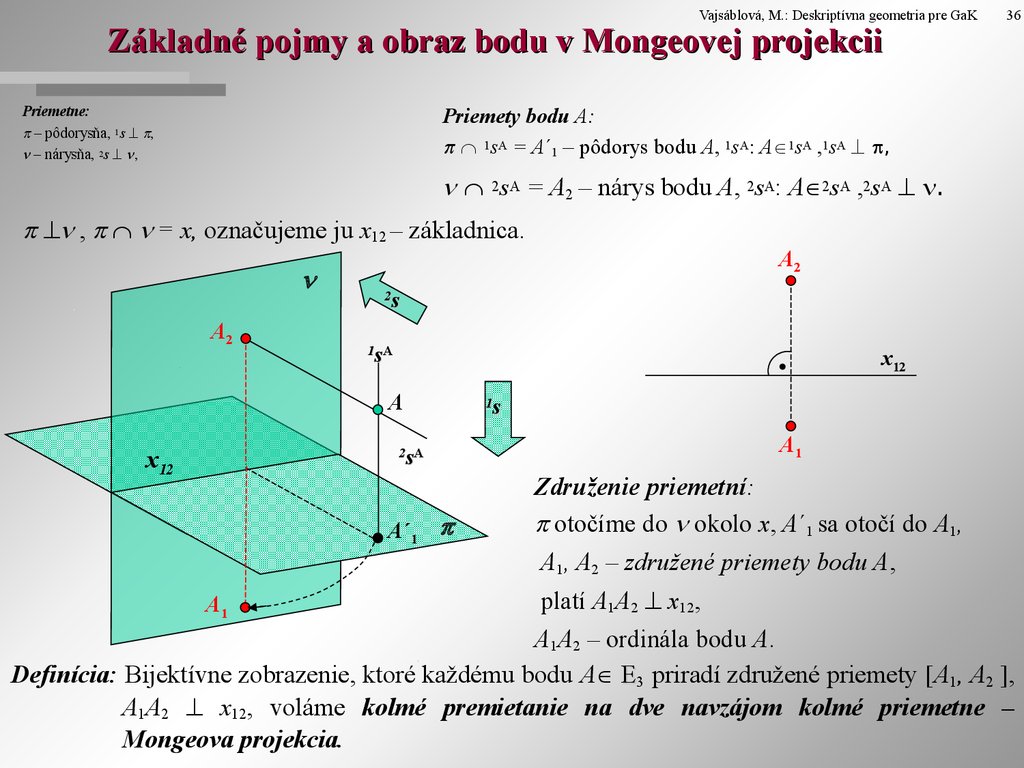
2. Základné pojmy a obraz bodu v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Základné pojmy a obraz bodu v Mongeovej projekcii
Priemetne:
– pôdorysňa, 1s ,
– nárysňa, 2s ,
36
Priemety bodu A:
1sA = A´1 – pôdorys bodu A, 1sA: A 1sA ,1sA ,
2sA = A2 – nárys bodu A, 2sA: A 2sA ,2sA .
, = x, označujeme ju x12 – základnica.
A2
A2
s
2
s
1 A
A
s
1
A1
s
x12
x12
2 A
A´1
Združenie priemetní:
otočíme do okolo x, A´1 sa otočí do A1,
A1, A2 – združené priemety bodu A,
A1
platí A1A2 x12,
A1A2 – ordinála bodu A.
Definícia: Bijektívne zobrazenie, ktoré každému bodu A 3 priradí združené priemety [A1, A2 ],
A1A2 x12, voláme kolmé premietanie na dve navzájom kolmé priemetne –
Mongeova projekcia.

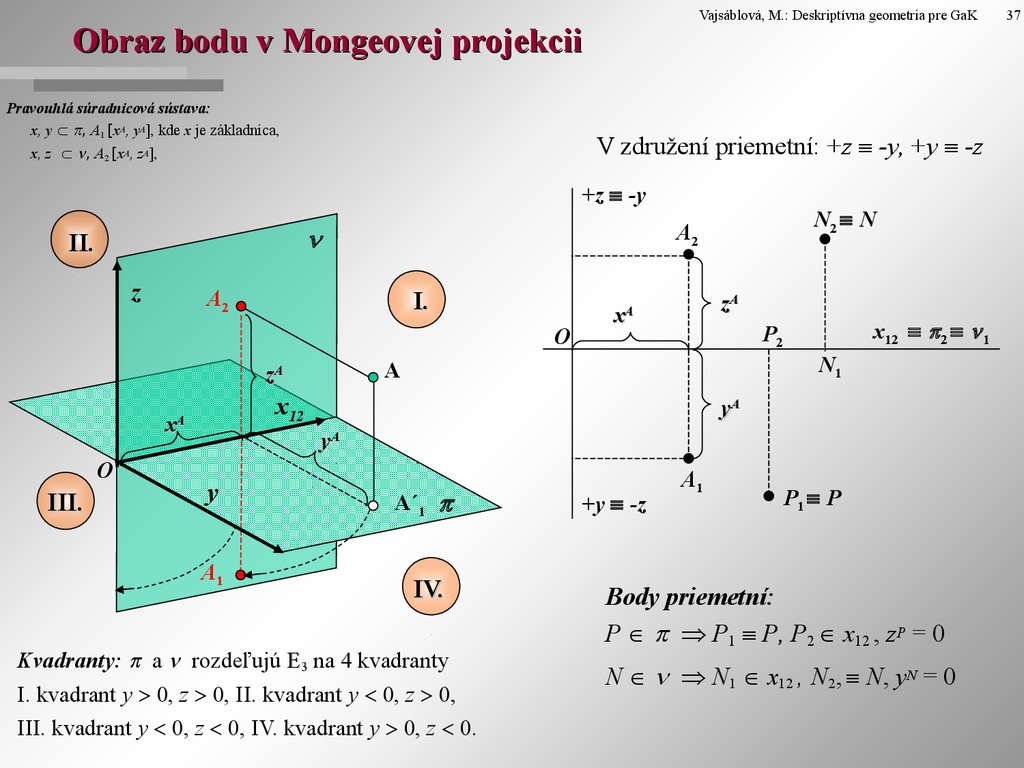
3. Obraz bodu v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Obraz bodu v Mongeovej projekcii
Pravouhlá súradnicová sústava:
x, y , A1 [xA, yA], kde x je základnica,
V združení priemetní: +z -y, +y -z
x, z , A2 [xA, zA],
+z -y
II.
z
A2
I.
O
III.
x12 2 1
P2
N1
x12
x
O
zA
xA
A
zA
A
N2 N
A2
yA
yA
y
A1
A´1
IV.
Kvadranty: a rozdeľujú 3 na 4 kvadranty
I. kvadrant y 0, z 0, II. kvadrant y 0, z 0,
III. kvadrant y 0, z 0, IV. kvadrant y 0, z 0.
+y -z
A1
P1 P
Body priemetní:
P P1 P, P2 x12 , zP = 0
N N1 x12 , N2, N, yN = 0
37

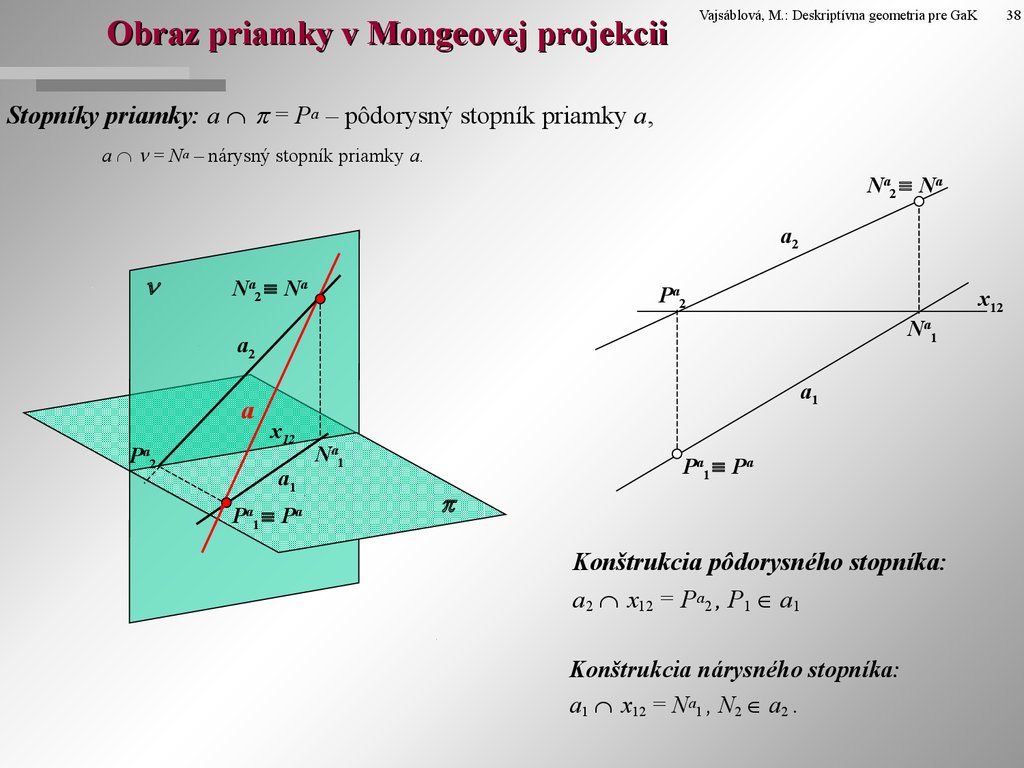
4. Obraz priamky v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Obraz priamky v Mongeovej projekcii
38
Stopníky priamky: a = Pa – pôdorysný stopník priamky a,
a = Na – nárysný stopník priamky a.
Na2 Na
a2
Na2 Na
Pa2
x12
Na1
a2
a
P2
a
a1
x12
a1
Pa1 Pa
Na1
Pa1 Pa
Konštrukcia pôdorysného stopníka:
a2 x12 = Pa2 , P1 a1
Konštrukcia nárysného stopníka:
a1 x12 = Na1 , N2 a2 .

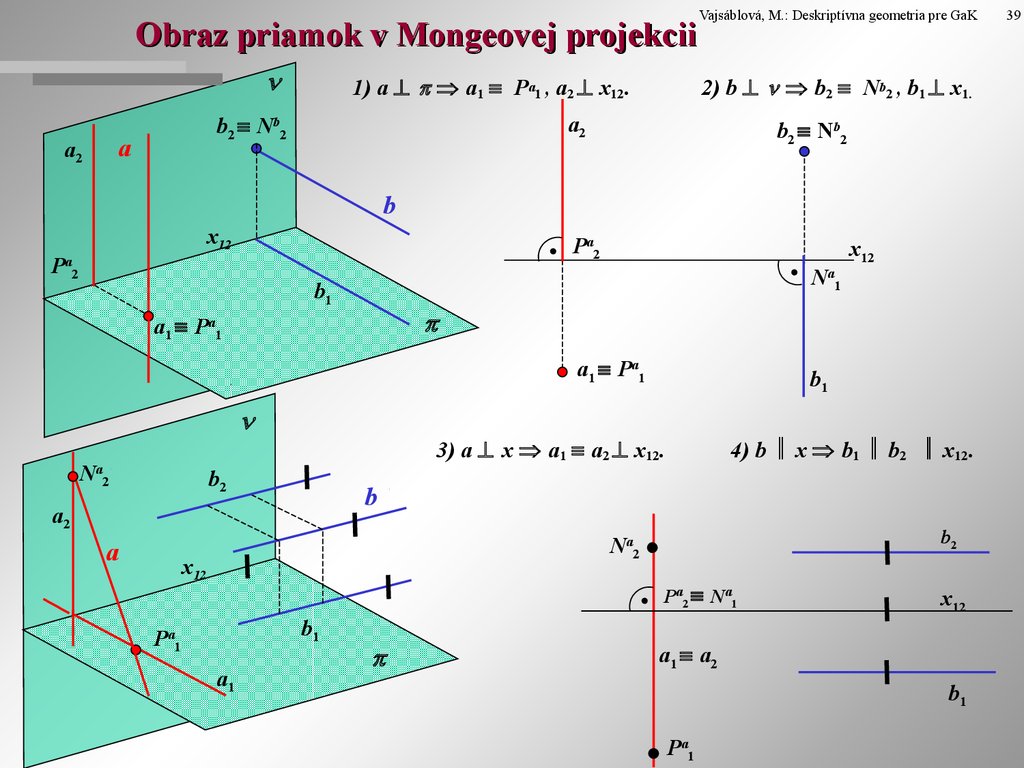
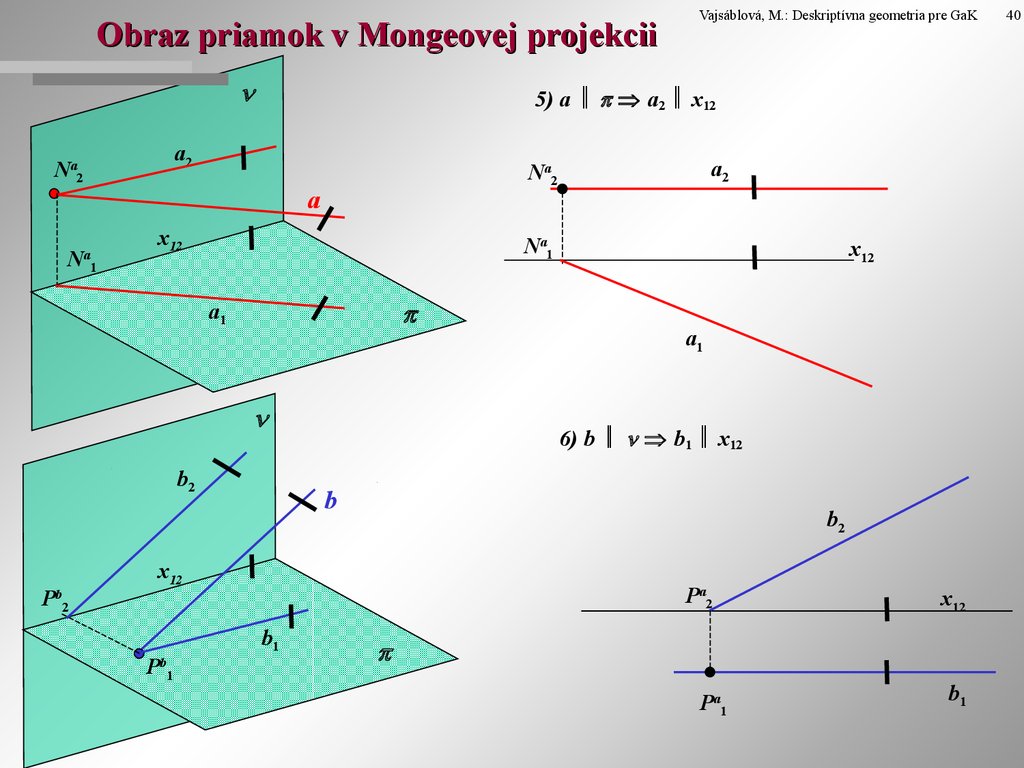
5. Obraz priamok v Mongeovej projekcii

b2 Nb2
a
a2
1) a a1 Pa1 , a2 x12.
Vajsáblová, M.: Deskriptívna geometria pre GaK
2) b b2 Nb2 , b1 x1.
a2
b2 Nb2
b
x12
P2
a
Pa2
b1
a1 Pa1
a1 Pa1
N2
a
4) b x b1 b2 x12.
b
a2
a
b1
3) a x a1 a2 x12.
b2
b2
Na2
x12
b1
Pa1
a1
N1
x12
a
Pa2 Na1
x12
a1 a2
b1
Pa1
39

6. Obraz priamok v Mongeovej projekcii

5) a a2 x12
a2
Na2
x12
Na1
a1
b2
Pb2
x12
a1
6) b b1 x12
b
b2
x12
Pa2
b1
Pb1
a2
Na2
a
Na1
Vajsáblová, M.: Deskriptívna geometria pre GaK
x12
Pa1
b1
40

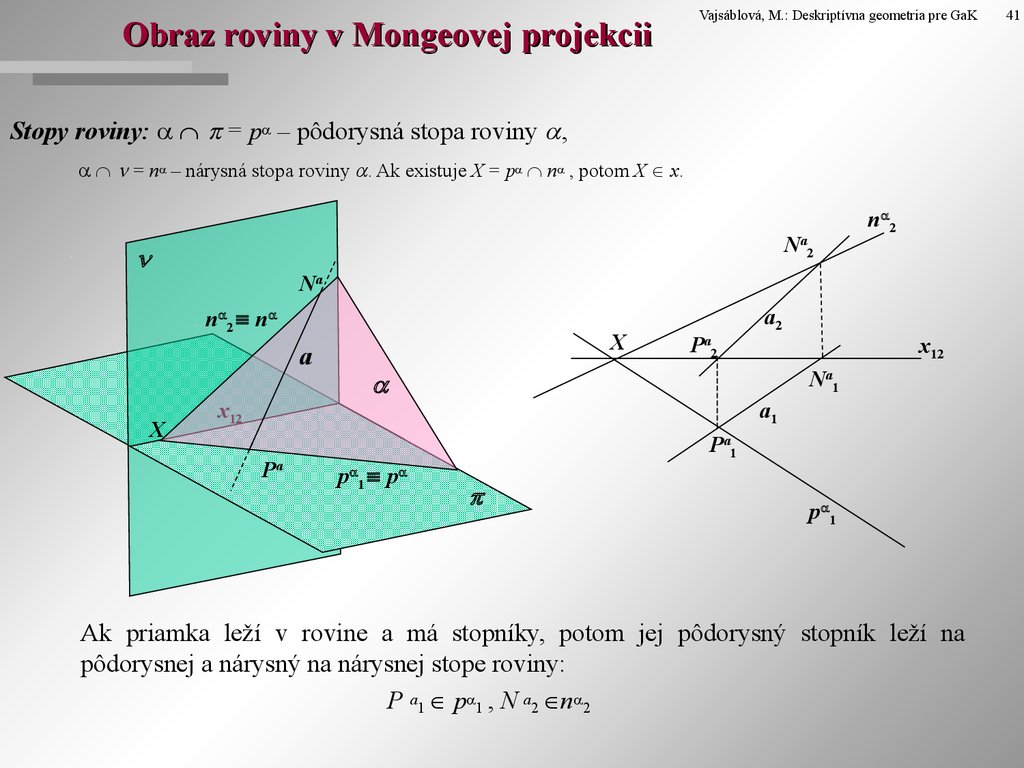
7. Obraz roviny v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Stopy roviny: = p – pôdorysná stopa roviny ,
= n – nárysná stopa roviny . Ak existuje X = p n , potom X x.
Na2
Na
n 2 n
a
X
n 2
x12
Pa
X
Pa2
x12
Na1
p 1 p
a2
a1
Pa1
p 1
Ak priamka leží v rovine a má stopníky, potom jej pôdorysný stopník leží na
pôdorysnej a nárysný na nárysnej stope roviny:
P a1 p 1 , N a2 n 2
41

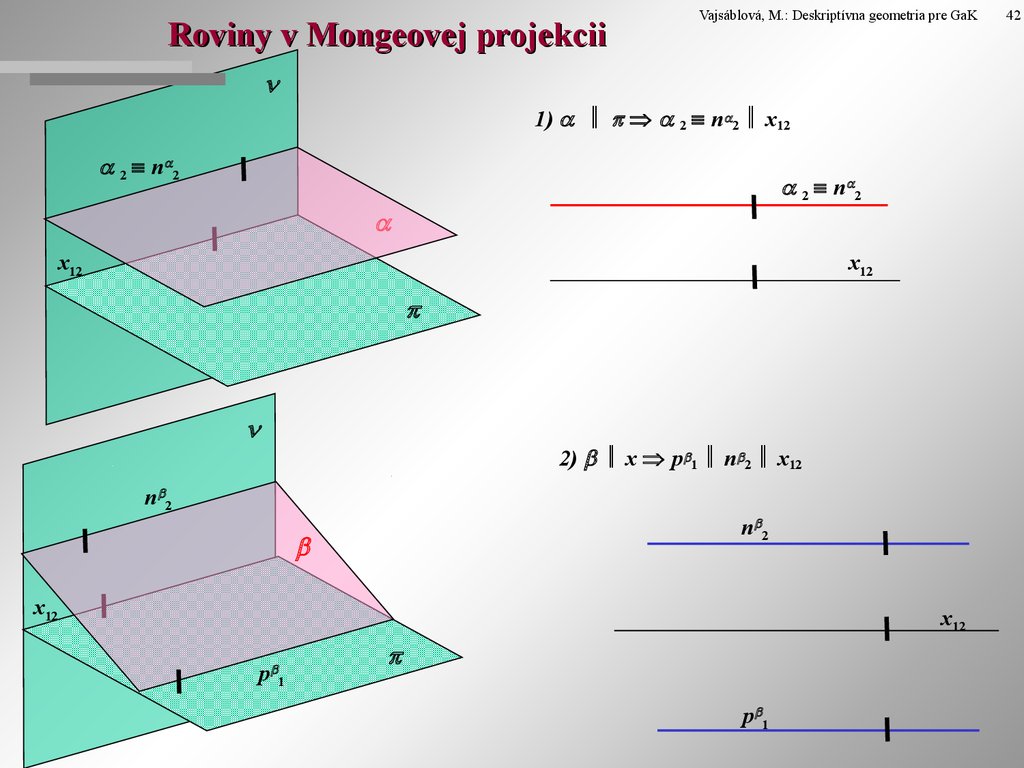
8. Roviny v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
1) 2 n 2 x12
2 n 2
2 n 2
x12
x12
2) x p 1 n 2 x12
n 2
n 2
x12
x12
p 1
p 1
42

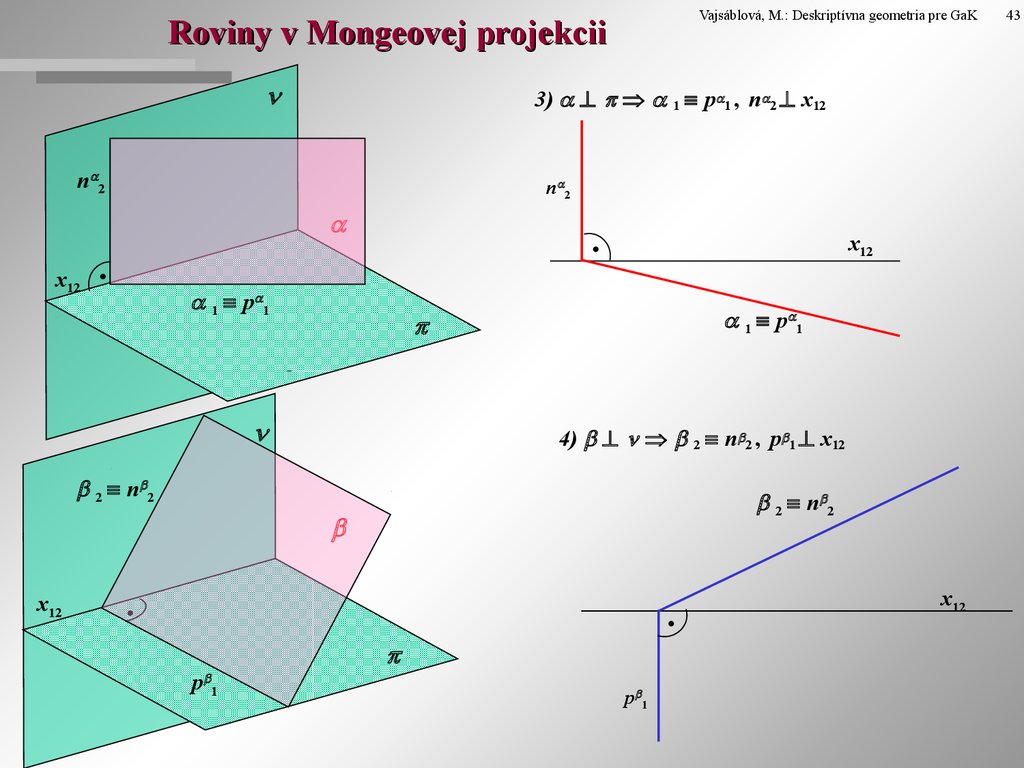
9. Roviny v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Roviny v Mongeovej projekcii
3) 1 p 1 , n 2 x12
n 2
n 2
x12
x12
1 p 1
1 p 1
4) 2 n 2 , p 1 x12
2 n 2
2 n 2
x12
x12
p 1
p 1
43

10. Hlavné a spádové priamky roviny v Mongeovej projekcii

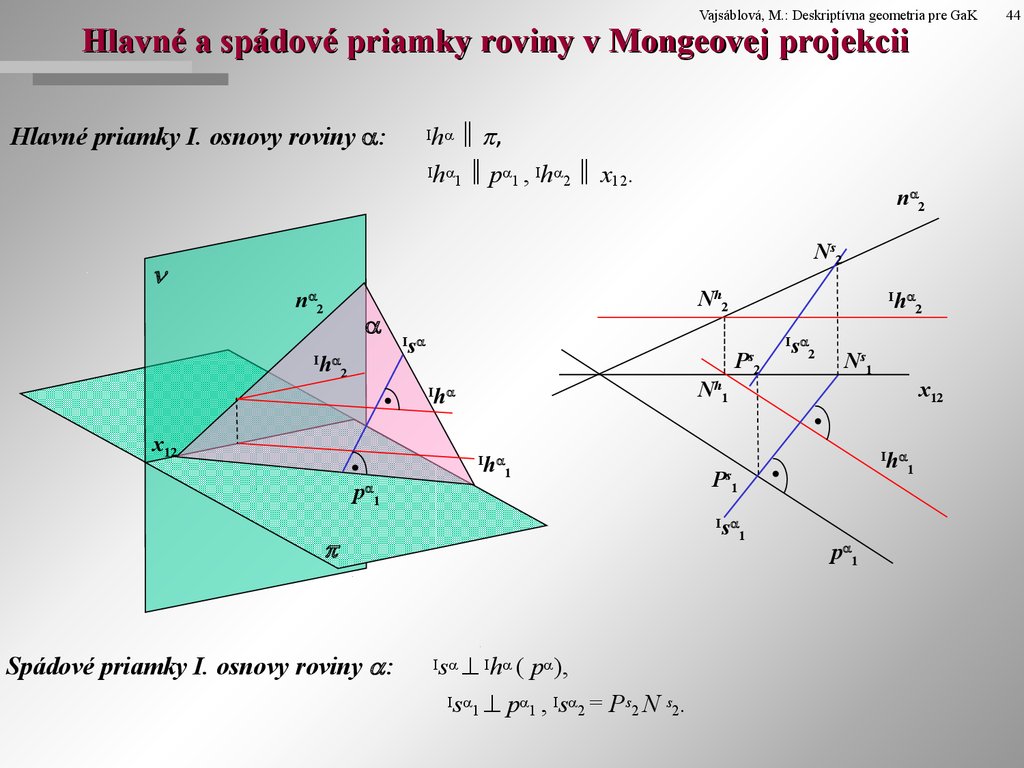
Vajsáblová, M.: Deskriptívna geometria pre GaK
Hlavné a spádové priamky roviny v Mongeovej projekcii
h ,
Ih p , Ih x .
1
1
2
12
Hlavné priamky I. osnovy roviny :
I
n 2
Ns2
n 2
Nh2
h
I
s
I
s
I
P
2
h
I
s
2
Nh1
h
I
2
Ns1
x12
x12
h
I
p
1
P
s
s Ih ( p ),
Is p , Is = Ps N s .
1
1
2
2
2
I
s
1
I
Spádové priamky I. osnovy roviny :
h
I
1
1
p 1
2
1
44

11. Hlavné a spádové priamky roviny v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
45
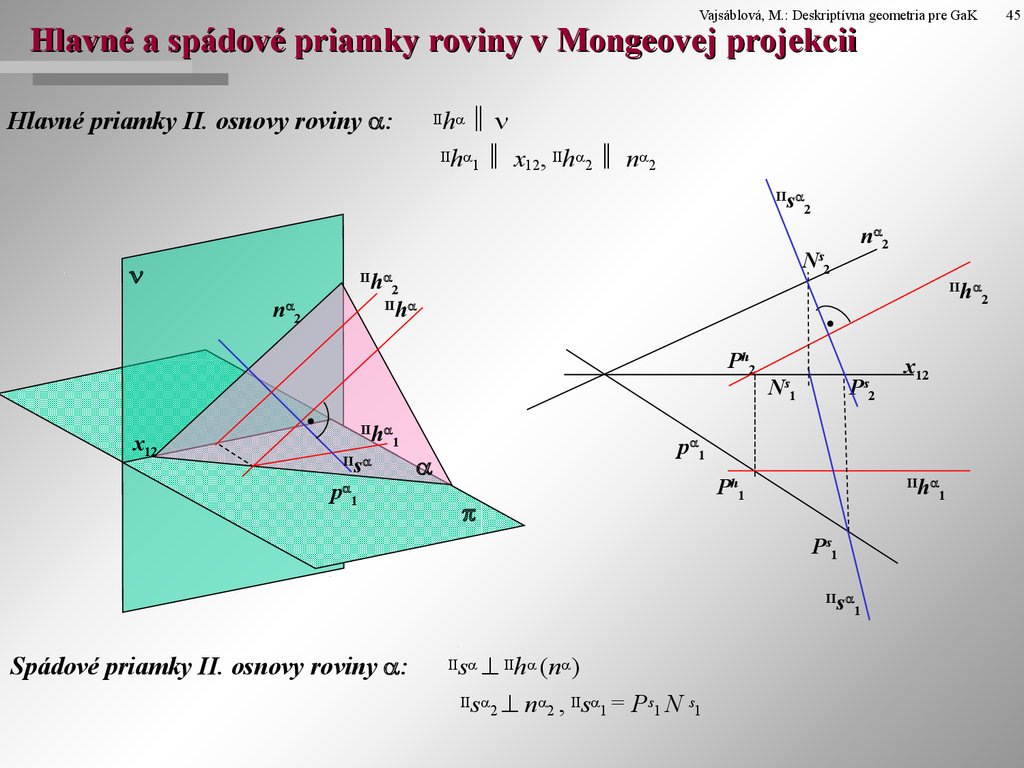
Hlavné a spádové priamky roviny v Mongeovej projekcii
Hlavné priamky II. osnovy roviny :
h
IIh x , IIh n
1
12
2
2
II
s
II
h
n
h
II
2
II
h
2
Ph2
h
II
x12
1
s
II
p
n 2
Ns2
II
2
1
N
P
s
1
x12
p 1
Ph1
h
II
Ps1
s
II
Spádové priamky II. osnovy roviny :
s
2
s IIh (n )
IIs n , IIs = Ps N s
2
2
1
1
1
II
1
1
2

12. Vzájomná poloha 2 priamok v Mongeovej projekcii

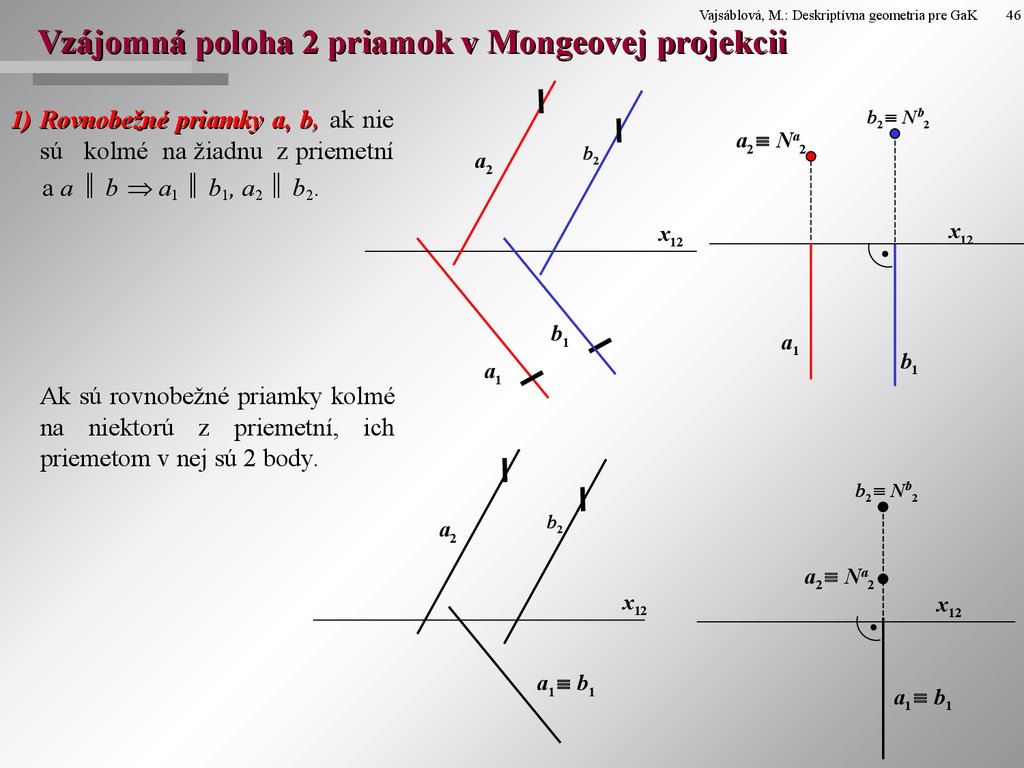
Vajsáblová, M.: Deskriptívna geometria pre GaK
Vzájomná poloha 2 priamok v Mongeovej projekcii
1) Rovnobežné priamky a, b, ak nie
sú kolmé na žiadnu z priemetní
a a b a1 b1, a2 b2.
a2 Na2
b2
a2
b 2 N b2
x12
x12
b1
a1
b1
a1
Ak sú rovnobežné priamky kolmé
na niektorú z priemetní, ich
priemetom v nej sú 2 body.
b2 Nb2
b2
x12
a2 Na2
x12
a2
a1 b1
a1 b1
46

13. Vzájomná poloha 2 priamok v Mongeovej projekcii

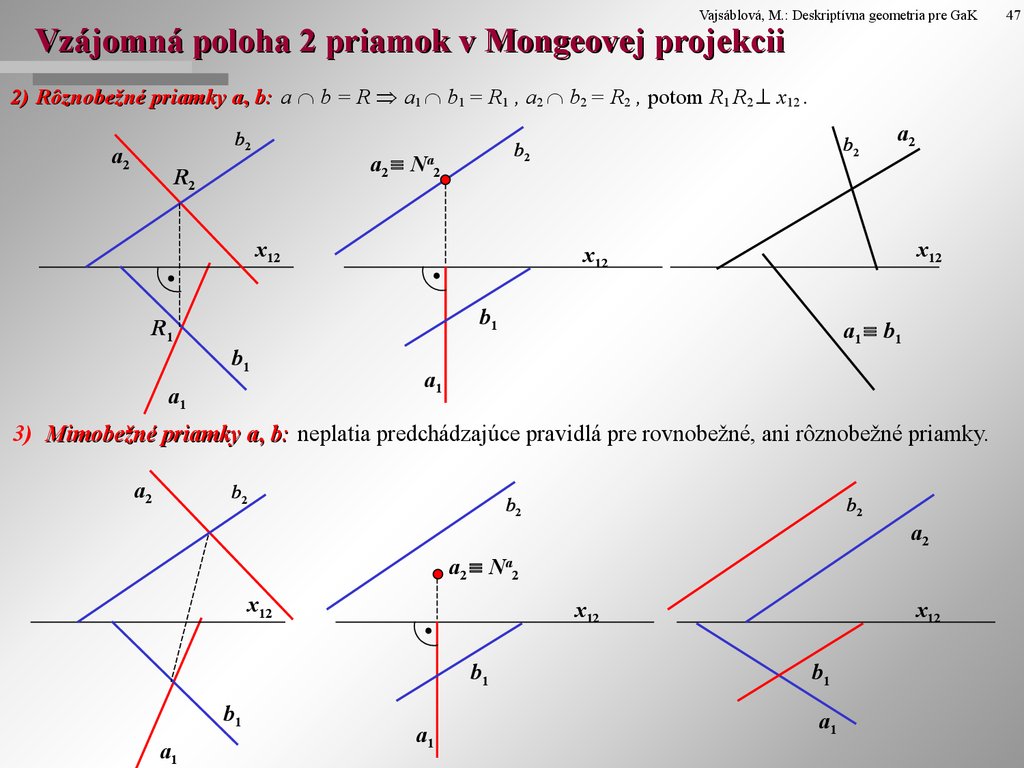
Vajsáblová, M.: Deskriptívna geometria pre GaK
Vzájomná poloha 2 priamok v Mongeovej projekcii
2) Rôznobežné priamky a, b: a b = R a1 b1 = R1 , a2 b2 = R2 , potom R1 R2 x12 .
b2
a2
a2 Na2
R2
b2
b2
x12
x12
x12
b1
R1
b1
a1
a2
a1 b1
a1
3) Mimobežné priamky a, b: neplatia predchádzajúce pravidlá pre rovnobežné, ani rôznobežné priamky.
a2
b2
b2
b2
a2
a2 Na2
x12
x12
b1
b1
a1
a1
x12
b1
a1
47

14. Vzájomná poloha 2 rovín v Mongeovej projekcii

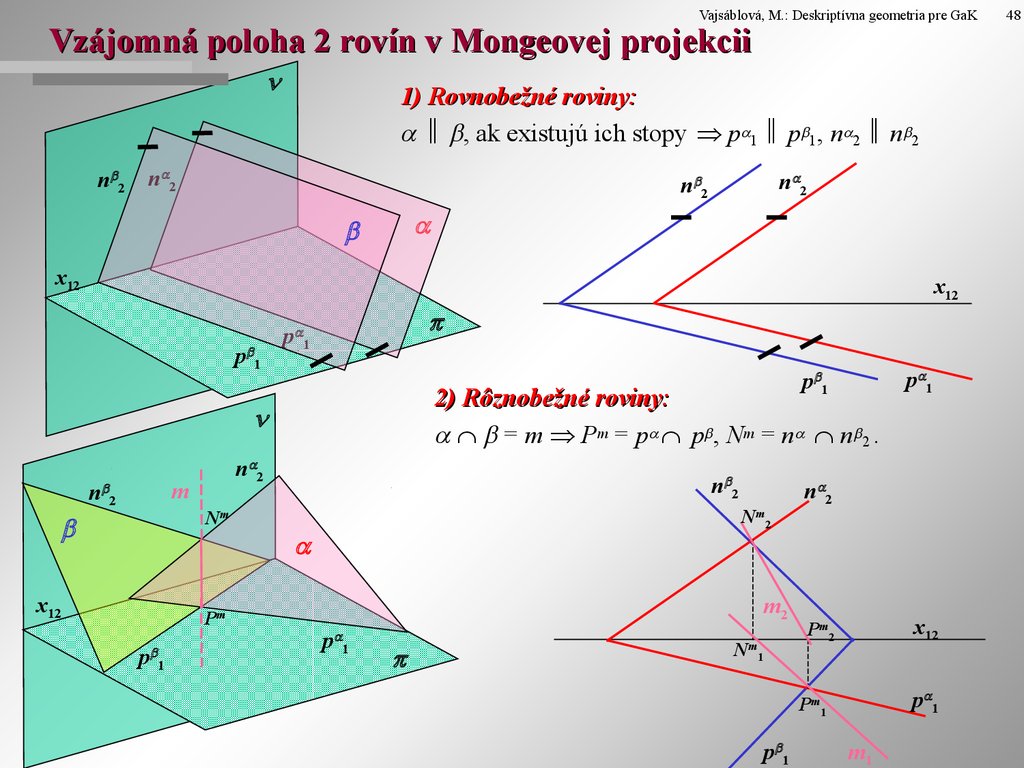
Vajsáblová, M.: Deskriptívna geometria pre GaK
Vzájomná poloha 2 rovín v Mongeovej projekcii
n 2
1) Rovnobežné roviny:
, ak existujú ich stopy p 1 p 1, n 2 n 2
n 2
n 2
n 2
x12
x12
p 1
p 1
p 1
2) Rôznobežné roviny:
= m Pm = p p , Nm = n n 2 .
n 2
m
n 2
Nm
x12
Pm
p 1
n 2
Nm 2
m2
p 1
N
m
p 1
n 2
x12
Pm2
1
p 1
Pm 1
p 1
m1
48

15. Vzájomná poloha priamky a roviny v Mongeovej projekcii

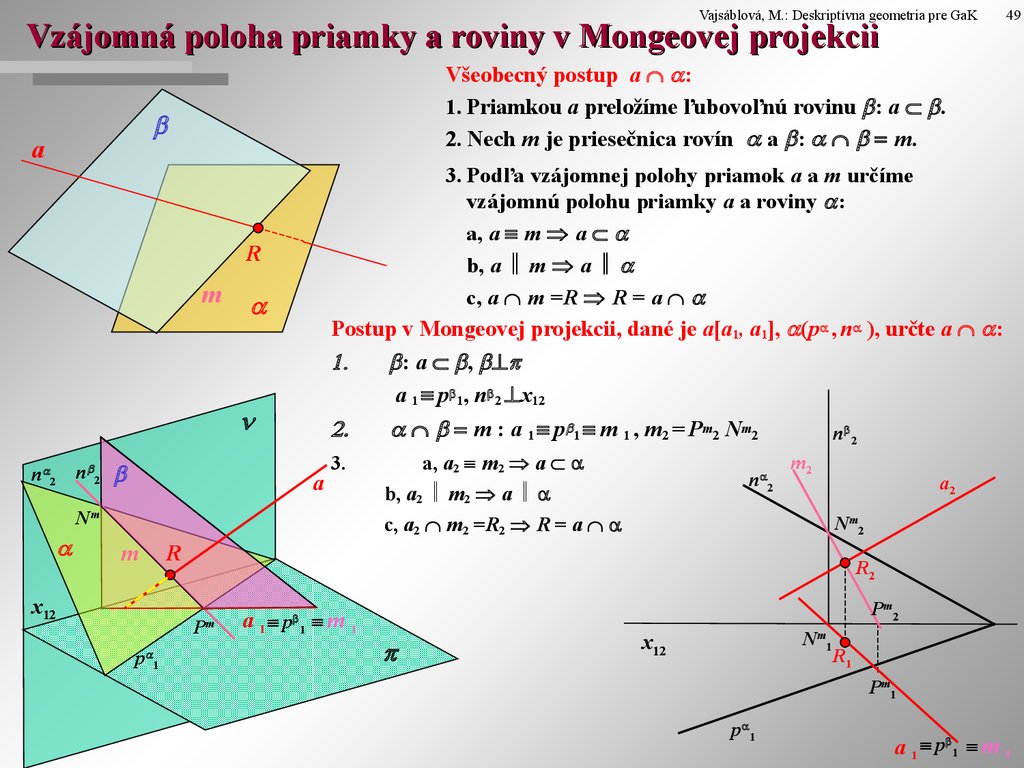
Vajsáblová, M.: Deskriptívna geometria pre GaK
Vzájomná poloha priamky a roviny v Mongeovej projekcii
Všeobecný postup a :
1. Priamkou a preložíme ľubovoľnú rovinu : a .
2. Nech m je priesečnica rovín a : m.
a
3. Podľa vzájomnej polohy priamok a a m určíme
vzájomnú polohu priamky a a roviny :
a, a m a
b, a m a
c, a m =R R = a
Postup v Mongeovej projekcii, dané je a[a1, a1], (p , n ), určte a :
R
m
n 2
n 2
a
1.
: a ,
a 1 p 1, n 2 x12
2.
m : a 1 p 1 m 1 , m2 = Pm2 Nm2
a, a2 m2 a
3.
Nm
n 2
b, a2 m2 a
n 2
m2
c, a2 m2 =R2 R = a
m
Nm 2
R2
P
p
a2
R
x12
1
49
m
a 1 p 1 m 1
Pm2
Nm 1
x12
R1
Pm1
p 1
a 1 p 1 m 1

16. Viditeľnosť priamky vzhľadom na rovinu v Mongeovej projekcii

Vajsáblová, M.: Deskriptívna geometria pre GaK
Viditeľnosť priamky vzhľadom na rovinu v Mongeovej projekcii
50
Viditeľnosť pôdorysu: Porovnávame bod na priamke a v rovine, ktorých pôdorysy sú totožné a viditeľný je
ten, ktorý má väčšiu z-tovú súradnicu:
1. a 1 p 1=A1 P 1, A a , P p
n 2n 2
N
2. A2 a2 , P 2 x12
3. zA zP bod A vidíme, teda
m
a
RA
m
x12
Pm a 1 p 1 m 1
p
vidíme polpriamku
1
n 2
m2
A2
n 2
R1 A1
R2
N1
a2
A´2 N2
x12
Pm 2
R1
A´1
Pm1 A1
a 1 p 1 m 1
p 1
Viditeľnosť nárysu: Porovnávame bod na priamke a v rovine, ktorých
nárysy sú totožné a viditeľný je ten, ktorý má väčšiu y-ovú súradnicu:
1. a 2 n 2=A´2 N2, A´ a, N n ,
2. A´1 a1 , N1 x12 ,
3. yA´ zN bod A vidíme, teda vidíme polpriamku
R 2 A´2 .