Mongeova projekcia

1. Snímek 1

Vajsáblová, M.: Deskriptívna geometria pre GaK
Margita Vajsáblová
54

2. Metóda: Sklápanie roviny kolmej na priemetňu

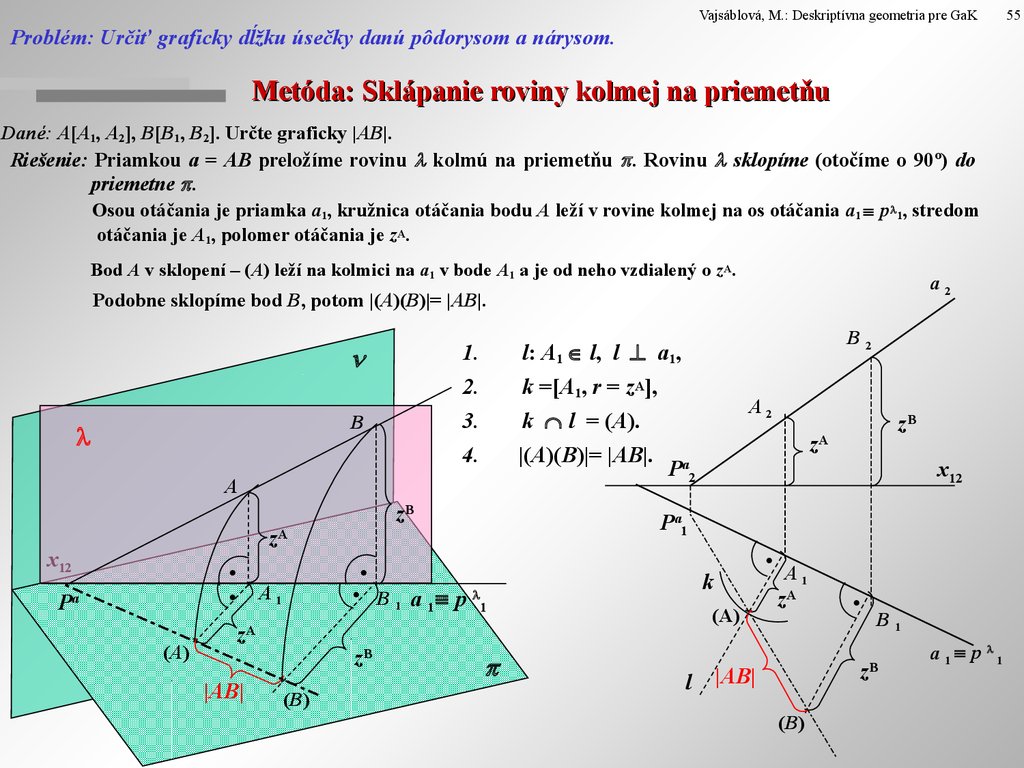
Vajsáblová, M.: Deskriptívna geometria pre GaK
Problém: Určiť graficky dĺžku úsečky danú pôdorysom a nárysom.
Metóda: Sklápanie roviny kolmej na priemetňu
Dané: A[A1, A2], B[B1, B2]. Určte graficky |AB|.
Riešenie: Priamkou a = AB preložíme rovinu kolmú na priemetňu . Rovinu sklopíme (otočíme o 90º) do
priemetne .
Osou otáčania je priamka a1, kružnica otáčania bodu A leží v rovine kolmej na os otáčania a1 p 1, stredom
otáčania je A1, polomer otáčania je zA.
Bod A v sklopení – (A) leží na kolmici na a1 v bode A1 a je od neho vzdialený o zA.
a2
Podobne sklopíme bod B, potom |(A)(B)|= |AB|.
B
A
zB
z
A1
(A)
zA
|AB|
zB
(B)
zB
zA
Pa
A2
x12
Pa1
A
x12
B2
l: A1 l, l a1,
k =[A1, r = zA],
k l = (A).
|(A)(B)|= |AB|. a
P2
1.
2.
3.
4.
k
B 1 a 1 p 1
(A)
l
A1
zA
B1
zB
|AB|
(B)
a 1 p 1
55

3. Metóda: Sklápanie roviny kolmej na priemetňu

Vajsáblová, M.: Deskriptívna geometria pre GaK
Problém: Určiť graficky uhol priamky s priemetňou.
Metóda: Sklápanie roviny kolmej na priemetňu
Definícia: Uhol priamky s priemetňou sa rovná uhlu priamky s jej kolmým priemetom do tejto
priemetne:
(a, ) = (a1, a)
[a]
(a, ) = (a2, a)
1.
2.
(a, ) = (a1, a) = (a1, (a))
[B]
yB
a2
(a, ) = (a2, a) = (a2, [a])
[A]
B2
yA
A2
B
A
(a, )
x
zB
z
Pa
(a, )
(a, )
(A)
P2
Pa1
A
Na2
A1
zA
|AB|
zB
(B)
B1 a1 p
1
x12
yB
(a, )
zA
a
Na1
zB
(A)
A1
zA
B1
z
|AB|
(B)
(a)
B
a 1 p 1
56

4. Snímek 4

Vajsáblová, M.: Deskriptívna geometria pre GaK
Problém: Určiť graficky uhol roviny s priemetňou.
Metóda: Sklápanie roviny kolmej na priemetňu
I. osnova
n 2
Definícia: Uhol roviny s priemetňou sa rovná uhlu jej
príslušnej spádovej priamky s priemetňou:
( , ) = (Is , )
( , ) = (IIs , )
( , )
x12
( , ) = (Is , ) = (Is 1, (Is ))
2.
1.
s
I
s
I
( , ) = (IIs , ) = (IIs 2, [IIs ])
p 1
1
s
II
2
n
n 2
Ns2
2
II. osnova
s
II
x12
( ,
)
p
1
s
I
Ps2
s
I
Ps1
2
x12
Ns1
1
( ,
) (Is )
p 1
(Ns)
57

5. Snímek 5

Vajsáblová, M.: Deskriptívna geometria pre GaK
58
Priamka kolmá na rovinu v Mongeovej projekcii
Dôsledok vety o kolmom priemete pravého uhla hovorí, že kolmý priemet kolmice na rovinu je kolmý
na príslušné hlavné priamky roviny, a teda na príslušnú stopu roviny, a teda nech (p , n ) a priamka
k , potom v Mongeovej projekcii platí:
k1 p 1 (Ih 1), tiež k1 Is 1,
k2 n 2 (IIh 1), tiež k2 IIs 2.
Kolmica na rovinu je kolmá aj na spádové priamky roviny, a teda nech k1 Is 1, potom platí, že ležia v
spoločnej premietacej rovine a v jej sklopení platí:
k2
(k) ( Is )
k
s
I
2
n
A2
h
I
x12
k1 Is 1
x12
A1
p 1
(A)
(Is )
n 2
Ps1
k1 s
I
1
p
(k)
1

6. Snímek 6

Vajsáblová, M.: Deskriptívna geometria pre GaK
Obraz kružnice v Mongeovej projekcii
a, kružnica k leží v rovine ´
k2
x12
k
k1
´
r
2´
x12
S1
k1 – kružnica
k2 – úsečka
k1
S2
k2
59

7. Snímek 7

Vajsáblová, M.: Deskriptívna geometria pre GaK
Obraz kružnice v Mongeovej projekcii
b, kružnica k leží v rovine
2 n 2
2
n
r
C2
k
k2
k2
S2 A2 B2
r
D2
x12
x12
k1
A1
r
S1
C1
D1
r
k1
B1
k2 – úsečka na n 2 , jej dĺžka C2D2 = 2r.
k1 – elipsa , ktorej hlavná os A1B1 na Ih 1, A1B1 = 2r,
vedľajšia os C1D na Is 1 .
I
1
h
p 1
60

8. Snímek 8

Vajsáblová, M.: Deskriptívna geometria pre GaK
Obraz kružnice v Mongeovej projekcii
c, kružnica k leží vo všeobecnej rovine
n
2
h
I
s
I
r
r
s
I
n 2
h
II
r
r
k2
A´2
h
I
p 1
1
2
h
I
1
r
B2
2
A2
S2
x12
B´2
A1
k1 , k2 – elipsy
k1 – elipsa – hlavná os A1B1 na h 1 , A1B1 = 2r,
- A2B2 na Ih 2 .
k2 – elipsa - hlavná os A´2B´2 na IIh 2 , A´2B´2 = 2r,
- A´1B´1 na IIh 1 .
- vedľajšia os C1D1 elipsy k1 na Is 1,
- vedľajšia os C´2D´2 na IIs 2.
Vedľajšie osi elíps dourčíme rozdielovou konštrukciou.
I
h
II
C1
1
B´1
A´1
B1
h
I
1
r
S1
k1
p 1
D1
61

9. Snímek 9

Vajsáblová, M.: Deskriptívna geometria pre GaK
Otočenie roviny kolmej na nárysňu do pôdorysne
2 n 2
A2
A
s
I
A20
x12
A0
s
I
1
P1s
A2
A1
p1
r
s1
• kružnica otáčania leží v rovine kolmej na
- p1 ; teda v premietacej rovine Is1 ;
r
A20
I
• Os otáčania - p1 ;
r
A0
x12
PS1
.
B0
• stred otáčania je P1s ; polomer je r = P2s A2 ;
• A0 Is1 ;
• perspektívna afinita s osou - p1 ; A1 A0,
v nej zobrazíme B B
2 n 2
p 1
A1
B1
62