Решение квадратных неравенств

1. РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ часть 1 Параграф 40-41 учебника

2. Домашнее задание

Параграф 40-41
№ 659 (весь)
№№ 660-662 (1, 3)
№ 665

3. Ссылка на видеоурок

https://youtu.be/5ewyFZZw0wM

4. Конспект видеоурока

5.

Квадратным неравенством называют неравенство вида:
2
ax bx c 0, (a 0)
Пример 1: Решить неравенство: a) x 2 2 x 3 0;
б ) x 2 2 x 3 0;
в) x 2 2 x 3 0;
г ) x 2 2 x 3 0;
Решение:
a) x2 2 x 3 0;
y x 2 2 x 3;
y 0 x 1 или x 3
( ; 1) (3; )
б ) x 2 2 x 3 0;
y x 2 2 x 3;
y 0 1 x 3
( 1;3)
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU

6.

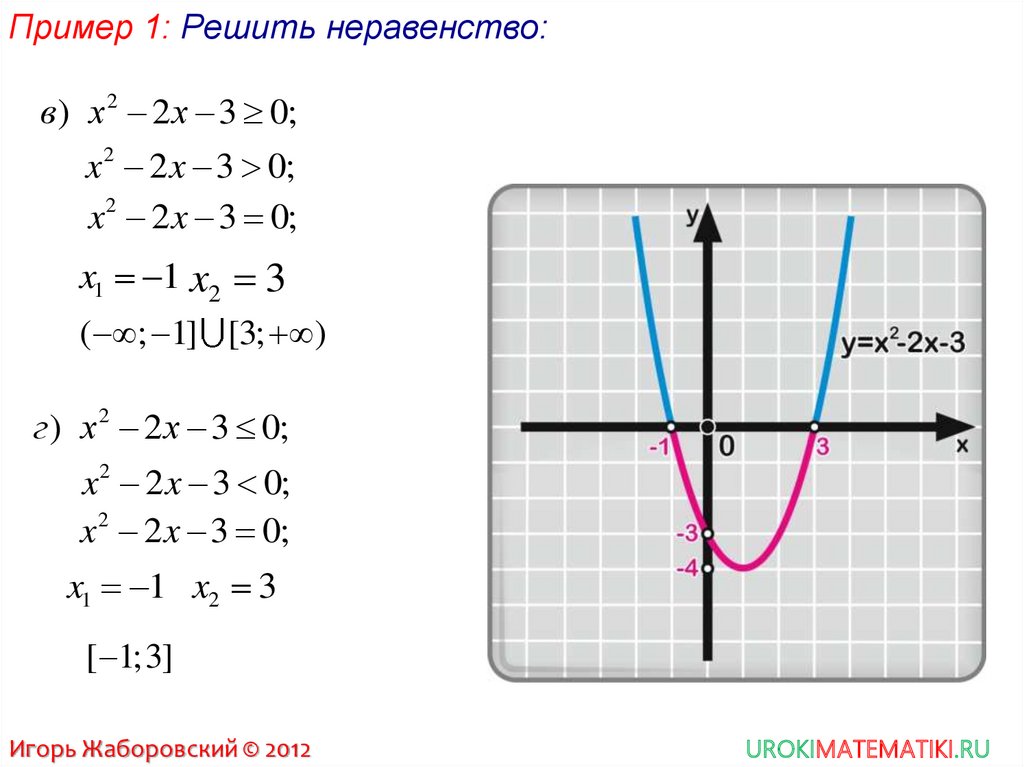
Пример 1: Решить неравенство:
в) x 2 2 x 3 0;
x 2 2 x 3 0;
x 2 2 x 3 0;
x1 1 x2 3
( ; 1] [3; )
г ) x 2 2 x 3 0;
x 2 2 x 3 0;
x 2 2 x 3 0;
x1 1 x2 3
[ 1;3]
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU

7.

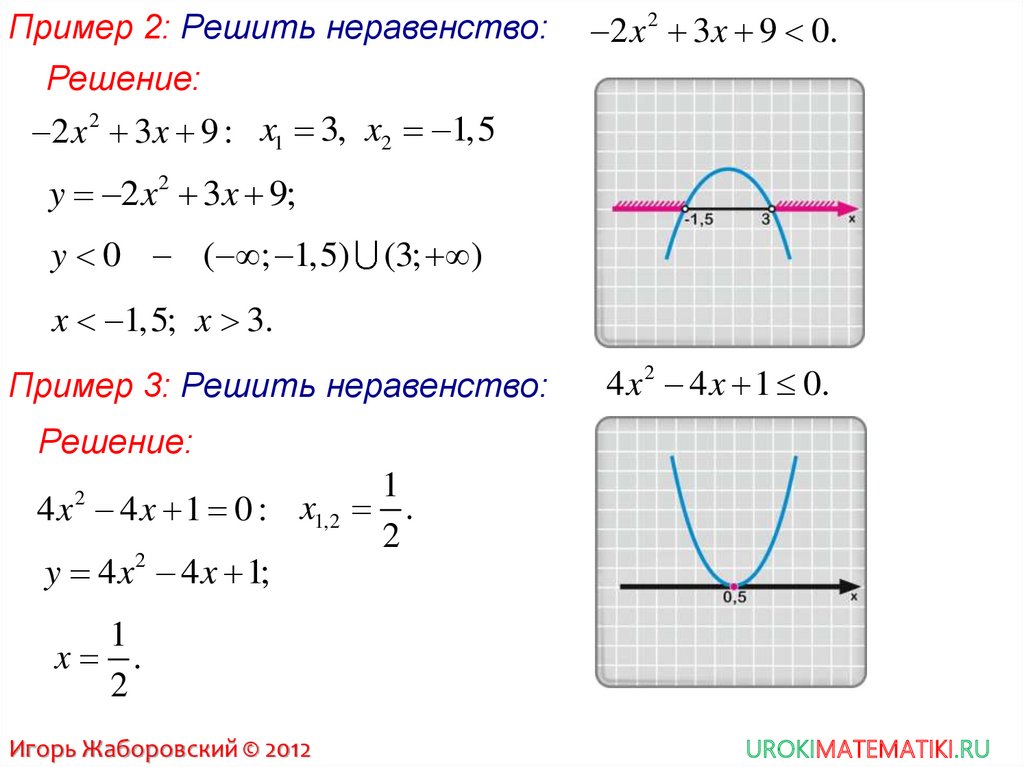
Пример 2: Решить неравенство:
2 x 2 3 x 9 0.
Решение:
2 x 2 3 x 9 : x1 3, x2 1,5
y 2 x2 3x 9;
y 0 ( ; 1,5) (3; )
x 1,5; x 3.
Пример 3: Решить неравенство:
4 x 2 4 x 1 0.
Решение:
1
4 x 4 x 1 0 : x1,2 .
2
2
y 4 x 4 x 1;
2
1
x .
2
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU

8.

Алгоритм решения квадратного неравенства
ax2+bx+c>0 ( ax2+bx+c>0)
1. Найти корни квадратного трехчлена ax2 + bх + с.
2. Отметить найденные корни на оси х и определить, куда
(вверх или вниз) направлены ветви параболы, служащей
графиком функции ax2 + bх + с; сделать набросок графика.
3. С помощью полученной геометрической модели определить,
на каких промежутках оси х ординаты графика положительны
(отрицательны); включить эти промежутки в ответ.
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU

9.

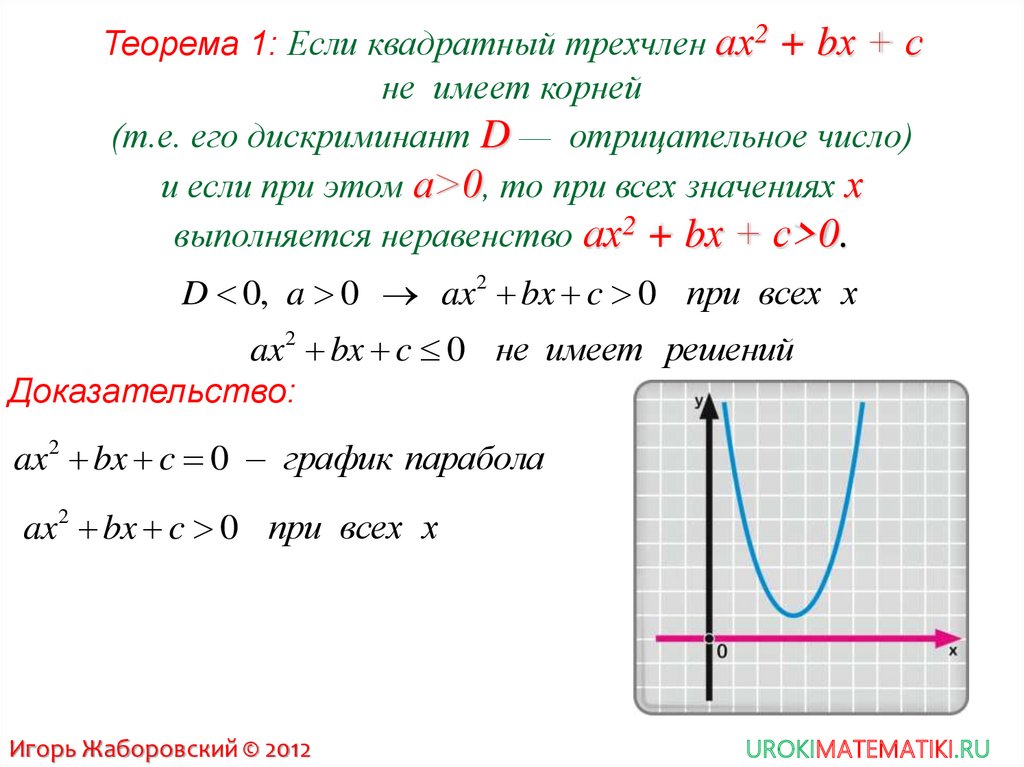
Теорема 1: Если квадратный трехчлен ах2 + bх + с
не имеет корней
(т.е. его дискриминант D — отрицательное число)
и если при этом а>0, то при всех значениях х
выполняется неравенство ах2 + bх + с>0.
D 0, a 0 ax 2 bx c 0 при всех х
ax 2 bx c 0 не имеет решений
Доказательство:
ax2 bx c 0 график парабола
ax2 bx c 0 при всех х
Игорь Жаборовский © 2012
UROKIMATEMATIKI.RU

English Русский Правила