Формулы корней квадратных уравнений

1. ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ часть 1

Игорь Жаборовский ©
UROKIMATEMATIKI.RU

2.

ax 2 bx c 0
b
2
2
2
ax bx c (ax bx) c a ( x x) c
a
2
2
2
2
b
b
4ac
b
b
b
2
.
a( x 2 x 2 )
c a x
2a
4a
2a
4a
4a
уравнения
b 2 4ac D - Дискриминант квадратного
2
b
D
2
.
ax bx c a x
2a 4a
2
b
D
a x ;
2a
4a
2
b
D
x 2 .
2a
4a
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

3.

Теорема 1: Если D < 0, то квадратное уравнение
ax2+bx+c=0 не имеет корней.
Доказательство:
2
b
D
x 2 .
2a
4a
D 0:
D
отрицательное число
2
4a
2
b
x неотрицательное число
2a
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

4.

Пример 1: Решить уравнение 2х2+4х+7=0.
Решение:
a 2, b 4, c 7,
D b 2 4ac 42 4 2 7 16 56 40 0
Уравнение корней не имеет
Теорема 2: Если D = 0, то квадратное уравнение
ax2+bx+c=0 имеет один корень,
b
который находится по формуле x
.
2a
2
Доказательство:
b
D
x 2 ;
D 0 :
2a
4a
2
b
b
b
x
.
x
0;
x 0;
2a
2a
2a
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

5.

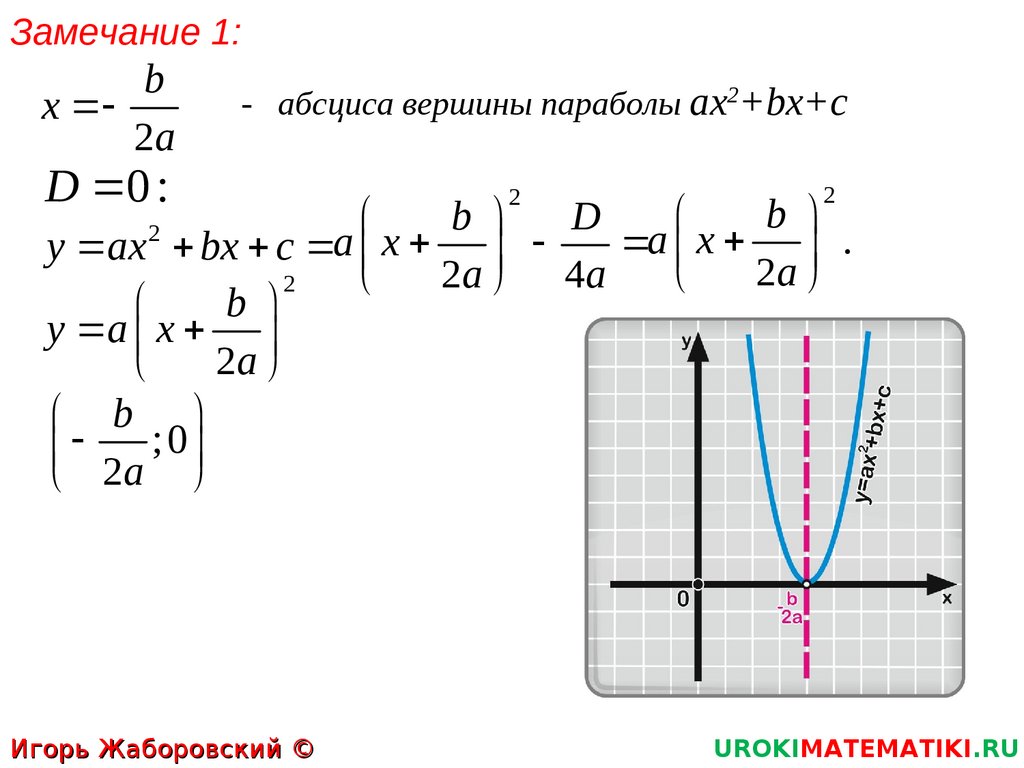
Замечание 1:
b
x
2a
- абсциса вершины параболы ах2+bх+с
D 0 :
2
2
b
b
D
a x .
y ax bx c a x
2a
2a 4a
2
b
y a x
2a
b
;0
2a
2
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

6.

Пример 2: Решить уравнение 4х2-20х+25=0.
Решение:
a 4, b 20, c 25,
2
D b 2 4ac ( 20) 4 4 25 400 400 0
b
x
;
2a
2,5
20
x
2,5
2 4
Замечание 2:
4х2-20х+25=0 - полный квадрат
4х2-20х+25=(2х-5)2;
(2х-5)2=0;
х=2,5.
2х-5=0;
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

7.

Теорема 3: Если D > 0, то квадратное уравнение
ax2+bx+c=0 имеет два корня,
которые находятся по формуле
b D
x1
,
Доказательство: 2a
b D
x2
.
2a
2
b
D
x 2 .
2a
4a
b
x
t ;
2a
D
t
;
2a
b
D
b
D
x
;
x
;
2a 2a
2a
2a
b
D b D
b
D b D
x1
; x2
.
2a 2a
2a
2a 2a
2a
Игорь Жаборовский ©
D
t 2;
4a
2
UROKIMATEMATIKI.RU

8.

Пример 3: Решить уравнение 3х2+8х-11=0.
Решение:
a 3, b 8, c 11,
D b 2 4ac 82 4 3 ( 11) 64 132 196;
D 0:
b D 8 196 8 14
1;
x1
6
2a
2 3
11
2
b D 8 196 8 14
3 .
x2
6
3
3
2a
2 3
1;
Игорь Жаборовский ©
2
3 .
3
UROKIMATEMATIKI.RU

9.

Алгоритм решения уравнения ах2+bх+с=0 :
1. Вычислить дискриминант D по формуле D = b2 - 4ас.
2. Если D < 0, то квадратное уравнение не имеет корней.
3. Если D = 0, то квадратное уравнение имеет один
корень:
b
x
2a
.
4. Если D > 0, то квадратное уравнение имеет два
корня:
b D
b D
x1
,
x2
.
2a
2a
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

10.

2
a
)
x
3 x 5 0;
Пример 4: Решить уравнение:
б ) 9 x 2 6 x 1 0;
Решение:
a ) x 2 3x 5 0;
в ) 2 x 2 x 3,5 0;
a 1, b 3, c 5,
D b 2 4ac 32 4 1 ( 5) 9 20 29;
D 0:
b D
3 29
b D
3 29
x1
; x2
.
2a
2
2a
2
б ) 9 x 2 6 x 1 0;
9 x 2 6 x 1 (3x 1) 2 ;
9 x 2 6 x 1 0;
(3 x 1) 2 0;
a 9, b 6, c 1,
3 x 1 0;
D b 2 4ac 36 36 0;
b
6
1
x
.
2a 2 9 3
Игорь Жаборовский ©
1
x .
3
UROKIMATEMATIKI.RU

11.

Пример 4: Решить уравнение:
в ) 2 x 2 x 3,5 0;
a 2, b 1, c 3,5,
D b 2 4ac 12 4 2 3,5 1 28 27;
D 0:
Уравнение корней не имеет
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

12.

b b 2 4ac
x1,2
2a
D b 2 4ac 0
2
D b 4ac 0
D b 2 4ac 0
-
КОРНЕЙ НЕТ
b 0
b
x1,2
2a
2a
-
ОДИН КОРЕНЬ
ДВА КОРНЯ
b b 2 4ac
x1
,
2a
Игорь Жаборовский ©
-
b b 2 4ac
x2
2a
UROKIMATEMATIKI.RU

13.

Пример 5: Решить уравнение:
Решение:
2 2 5
7
a) x x
0;
3
6
12
2
5
7
a , b , c ,
3
6
12
7
2 2 5
12 x x
12 0;
6
12
3
8 x 2 10 x 7 0;
10 100 224 10 324 10 18
;
x1,2
16
16
16
10 18 1
x1
;
16
2
Игорь Жаборовский ©
10 18
7
x2
.
16
4
UROKIMATEMATIKI.RU

14.

Пример 5: Решить уравнение:
б ) 3 x 2 0, 2 x 2, 77 0;
a 3, b 0, 2, c 2, 77,
300 x 2 20 x 277 0;
20 202 4 300 277
x1,2
.
2 300
Уравнение корней не имеет
Игорь Жаборовский ©
UROKIMATEMATIKI.RU

15.

Пример 6: Решить уравнение
5 x 2 2 15 x 1 0.
Решение:
a 5, b 2 15, c 1,
D b 2 4ac ( 2 15) 2 4 5 1 60 20 40 0
b D 2 15 40 2 15 2 10 2 5 3 2
x1
10
10
2a
2 5
3 2
.
5
5
5
b D 2 15 40
x2
2a
2 5
Игорь Жаборовский ©
3 2 .
5
UROKIMATEMATIKI.RU

16.

Пример 7: Решить уравнение x 2 (2 p 1) x ( p 2 p 2) 0.
Решение:
Уравнение с параметром
D (2 p 1) 2 4 1 ( p 2 p 2) (4 p 2 4 p 1) (4 p 2 4 p 8) 9;
2 p 1 3 2 p 2 p 2;
(2 p 1) 9
x1
2
2
2
(2 p 1)
x2
2
9
Игорь Жаборовский ©
2 p 1 3 2( p 1)
p 1;
2
2
UROKIMATEMATIKI.RU

17.

Пример 8: Решить уравнение px 2 (1 p ) x 1 0.
Решение:
p 0 :
0 x 2 (1 0) x 1 0;
x 1 0;
x 1;
(1 p) (1 p ) 2 4 p ( 1)
p 0 : x1,2
2p
p 1 1 2 p p 2 4 p p 1 ( p 1) 2 p 1 ( p 1)
;
2p
2p
2p
p 1: D 0 x1 x2 1;
p 1 ( p 1) 2 p
p 1 ( p 1) 2
1
1; x2
;
p 1: x1
2p
2p
2p
2p
p
если p 0 или p 1, то x 1;
1
если p 0 или p 1, то x1 1, x2 .
p
Игорь Жаборовский ©
UROKIMATEMATIKI.RU