Похожие презентации:
Производная функции
1. Производная функции
Разработал: преподавательПроскурякова И.С.
2. Цели и задачи
изучить понятие приращенияфункции и приращения аргумента;
изучить понятие определение
производной функции в точке хо;
познакомить с формулами и
правилами дифференцирования
научить вычислять производную
функции.
3. Приращение функции и аргумента
х = х – хо – приращениеаргумента
f(х) = f(х) – f(хо)
f(х) = f (хо + х ) – f(хо)
приращение
функции
–
4. Пример
Найдите х, f, если f(х) = х2,хо = 1, х = 1,5
Решение:
х = х – хо =1,5-1=0,5 – приращение аргумента
f(х) = f(х) – f(хо)
f(хо) = f(1) = 12 = 1,
f (х) = f(1,5) = f(1,5) = 1,52 = 2,25,
f = 2,25 – 1 = 1,25.
Ответ: f = 1,25
5. Определение производной
f ′(xо) –f
f ( xo )
x
число
при условии при ∆х → 0
6.
Операцию вычисления производнойфункции называют
дифференцированием функции.
7. у = х2
у=2
х
у(хо) = хо2,
у(хо + ∆х) = (хо + ∆х)2= хо2 + 2 хо ∆х + (∆х)2,
∆у = у(хо + ∆х) – у(хо) = хо2 + 2 хо ∆х +
+ (∆х)2 – хо2 = 2 хо ∆х + (∆х)2 = ∆х(2хо + ∆х),
∆у
∆х (2хо + ∆х)
=
= 2хо + ∆х → 2хо
∆х
∆х
при ∆х → 0
2
′
Ответ: (х ) = 2х
8. у = х3
у=3
х
у(хо) = хо3
у(хо + ∆х) =
3 + зх 2 ∆х + зх (∆х)2 + (∆х)3
х
= о
о
о
∆у = у(хо + ∆х) – у(хо) =
2 + зх ∆х + (∆х)2)
∆х(зх
=
о
о
∆у
→ зхо2
3′
2
∆х
(х ) = 3х
9. у = kх + в
у(хо) = kхо + в,у(хо + ∆х) = k ∙ (хо + ∆х) + в = k хо +
+ k∆х + в,
∆у = у(хо + ∆х) – у(хо) = k хо + k∆х +
+ в – kхо – в = k∆х,
∆y k∆х
=
= k.
∆x
∆x
Ответ: (kх + в)′ = k
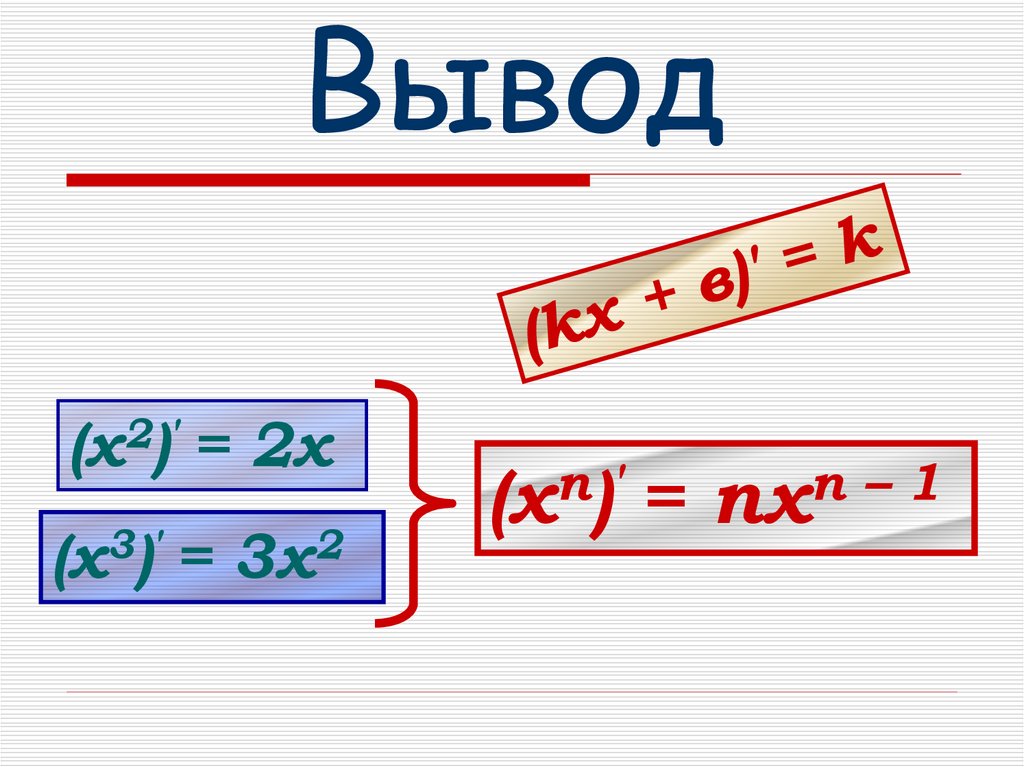
10. Вывод
2′
(х )
= 2х
(х3)′ = 3х2
n
′
(x )
=
n
–
1
nx
11. Найди производную!
1.2.
3.
4.
5.
(х7)′=7х6
(х9)′=9х8
(- 7)′=0
(9х + 16)′=9
(7 – 4х)′=-4











 Математика
Математика








