Похожие презентации:
Непрерывные случайные величины
1.
Случайна величина Х называется непрерывной,если невозможно перечислить все ее значения
2.
Случайна величина Х называется непрерывной,если невозможно перечислить все ее значения
Например, X – время работы электролампочки до
перегорания
X – рост случайно выбранного человека
3.
Вместо вероятности того, чтослучайная величина Х примет значение,
равное х, т.е. p(X=x), рассматривают P( X
F ( x ) P( X x )
Функция распределения
x)
4.
Известно, что студент приходит на занятия вслучайный момент времени в интервале от
8.00 до 9.00. Пусть X – Время прихода
студента. Найдем функцию распределения X.
5.
F ( x ) P( X x )событие
8.00
X x
x
9.00
( x 8)
F ( x)
x 8
1
если
x 8;9
6.
F ( x ) P( X x )F ( x) 0
если
x 8
7.
F ( x ) P( X x )F ( x) 0
если
F ( x) 1
если
x 8
x 9
8.
F ( x ) P( X x )0, x 8
F ( x) x 8, x (8;9]
1, x 9
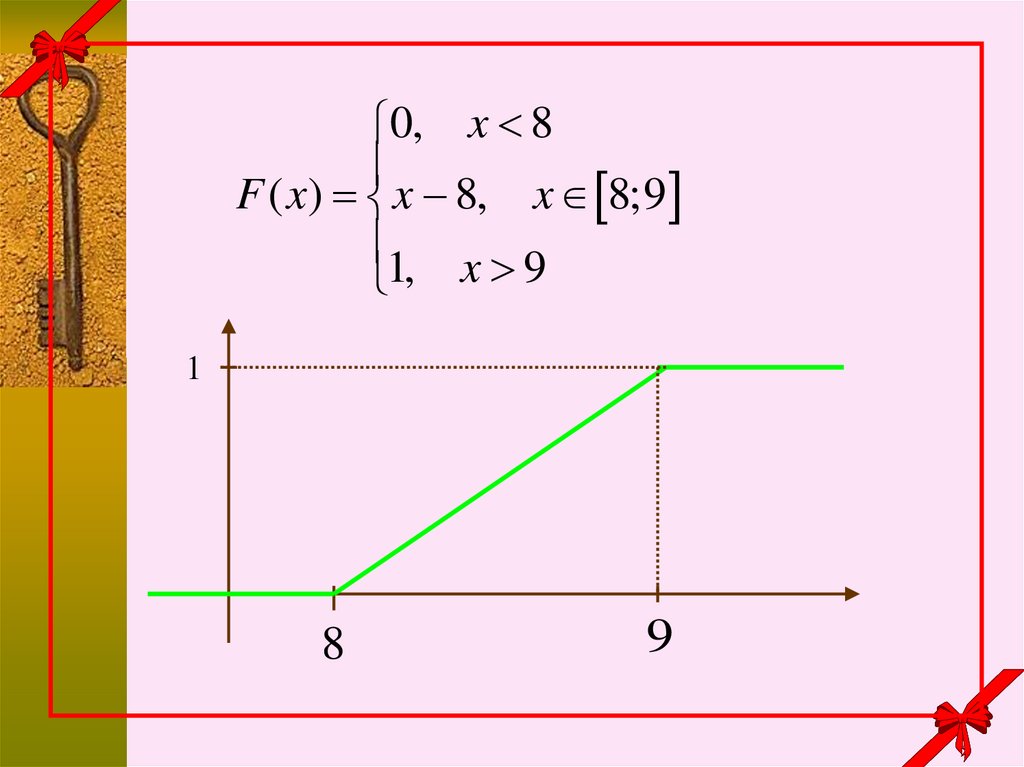
9.
0, x 8F ( x) x 8, x 8;9
1, x 9
1
8
9
10.
Автобусы ходят с интервалом 20 минут. Пассажирподходит к остановке в случайный момент
времени. Пусть Х – время ожидания автобуса
пассажиром.
Найти функцию распределения Х и построить ее
график.
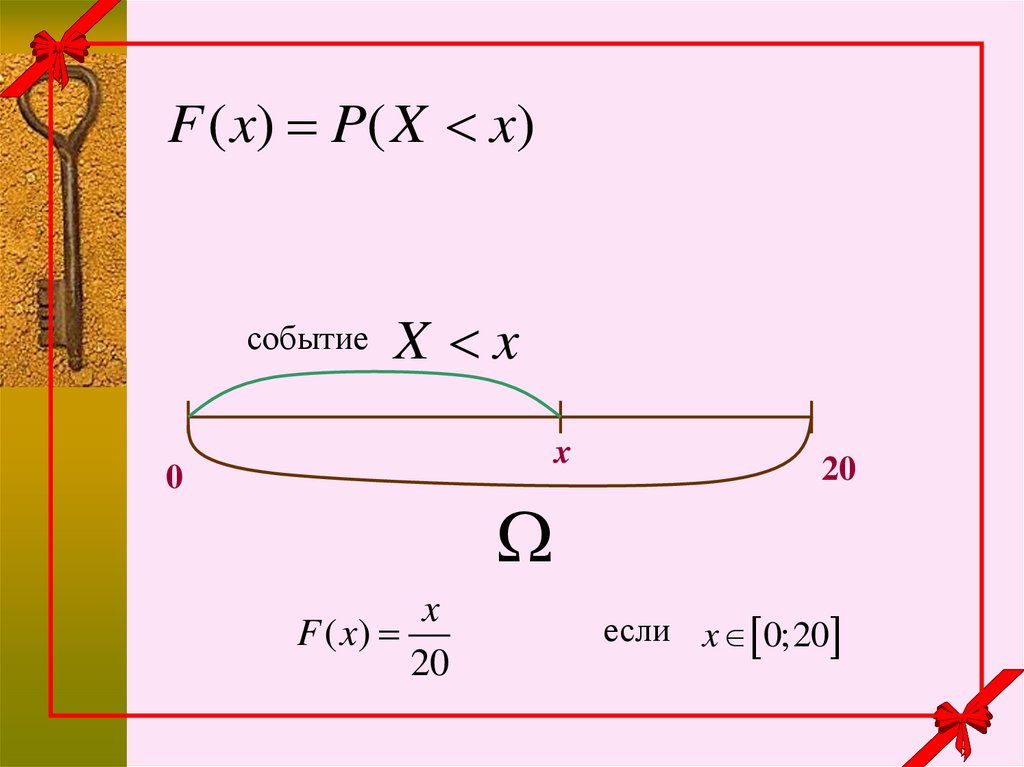
11.
F ( x ) P( X x )событие
X x
x
0
x
F ( x)
20
20
если x 0;20
12.
F ( x ) P( X x )F ( x) 0
если
x 0
13.
F ( x ) P( X x )F ( x) 0
F ( x) 1
если
x 0
если
x 20
14.
F ( x ) P( X x )0, x 0
x
F ( x) , x (0;20]
20
1, x 20
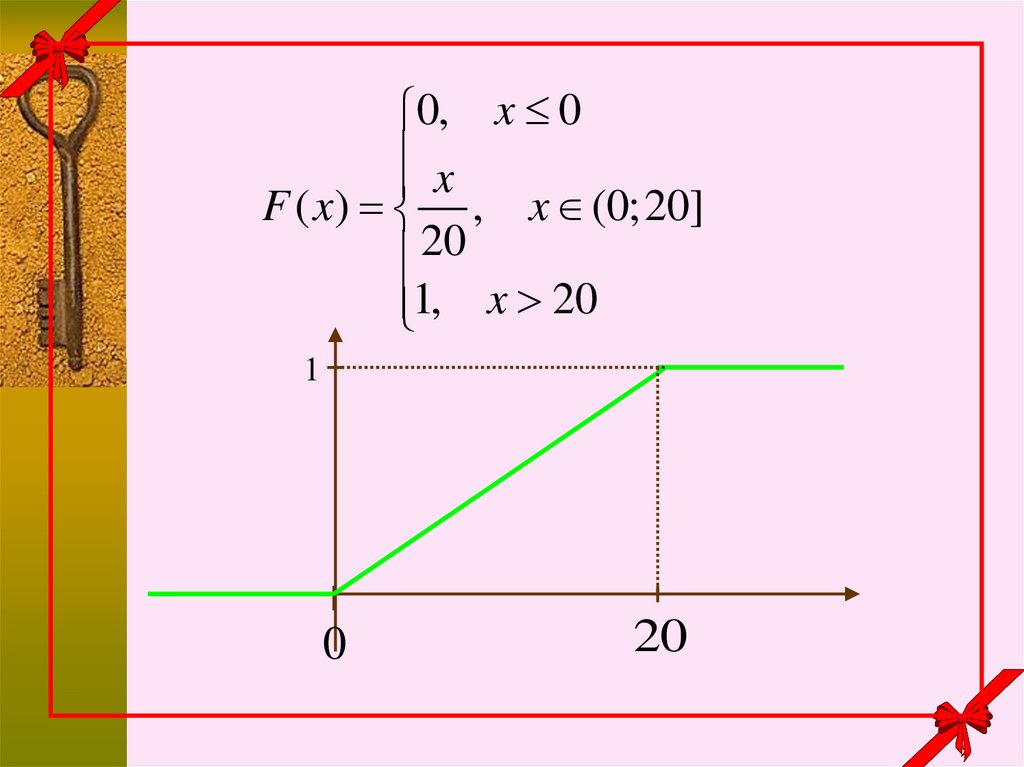
15.
0, x 0x
F ( x) , x (0;20]
20
1, x 20
1
0
20
16.
1Функция распределения является
неубывающей
функцией. Для
любых x1 x2 выполнено
F ( x1 ) F ( x2 )
17.
2На минус бесконечности функция
распределения равна нулю:
F ( ) 0
18.
3На плюс бесконечности функция
распределения равна единице:
F ( ) 1
19.
4p( X ) F ( ) F ( )
20.
5p( X ) 1 F ( )
21.
Пример Используя функцию распределениявеличины X – Время прихода студента на
лекцию, найти вероятность того, что он
прибудет в интервал времени от 8.30 до 8.40.
0, x 8
F ( x) x 8, x 8;9
1, x 9
22.
Рассмотримнепрерывную
случайную
величину Х с функцией распределения F(x).
Вычислим вероятность попадания этой
случайной величины на промежуток
[ x; x x]
23.
Рассмотримнепрерывную
случайную
величину Х с функцией распределения F(x).
Вычислим вероятность попадания этой
случайной величины на промежуток
[ x; x x]
p( x X x x) F ( x x) F ( x)
Рассмотрим предел
F ( x x) F ( x)
lim
x 0
x
=
24.
По определению производной этот пределравен производной функции F(x) :
=
F ( x) f ( x)
Функция f(x), равная производной
от функции распределения, называется
плотностью вероятности случайной
величины Х.
25.
F ( x x) F ( x)f ( x) lim
x 0
x
f ( x) x F ( x x) F ( x)
P ( x X x x )
При малых x величина f ( x) x
приближенно показывает вероятность попадания в
[ x; x x]
26.
Пример Дана функция распределения.0, x 0
x
F ( x) , x (0;20]
20
1, x 20
Найти плотность распределения
27.
Пример Дана функция распределения.0, x 0
x
F ( x) , x (0;20]
20
1, x 20
0, x 0
1
f ( x) F ( x) , x (0; 20]
20
0, x 20
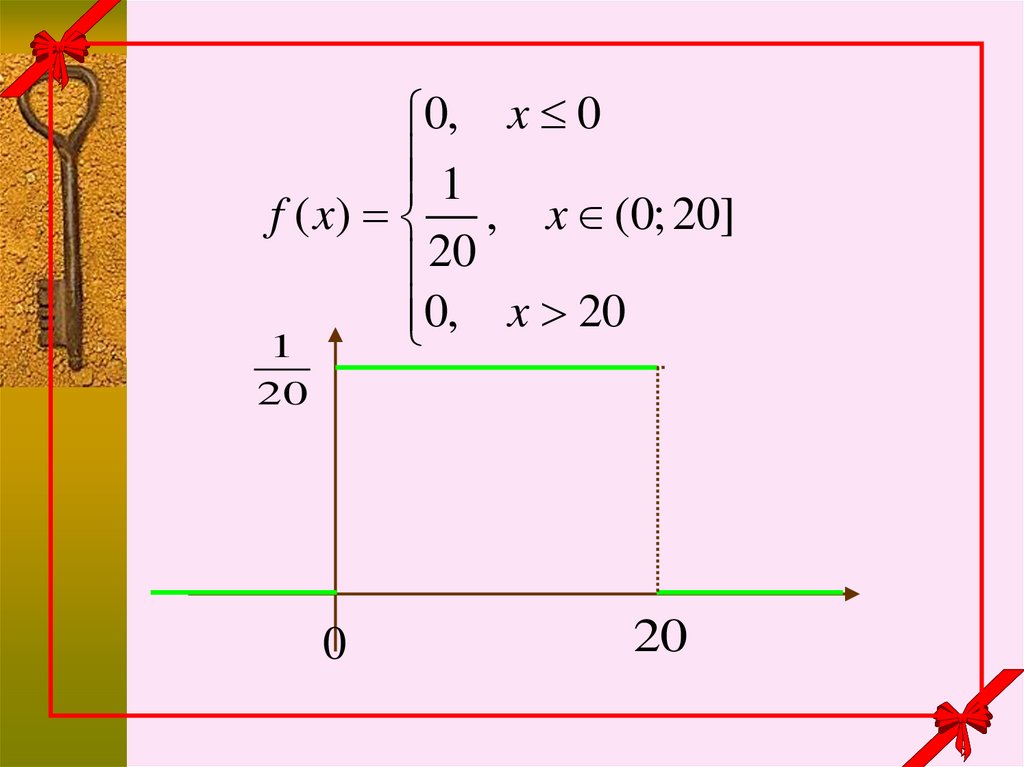
28.
0, x 01
f ( x) , x (0; 20]
20
0, x 20
1
20
0
20
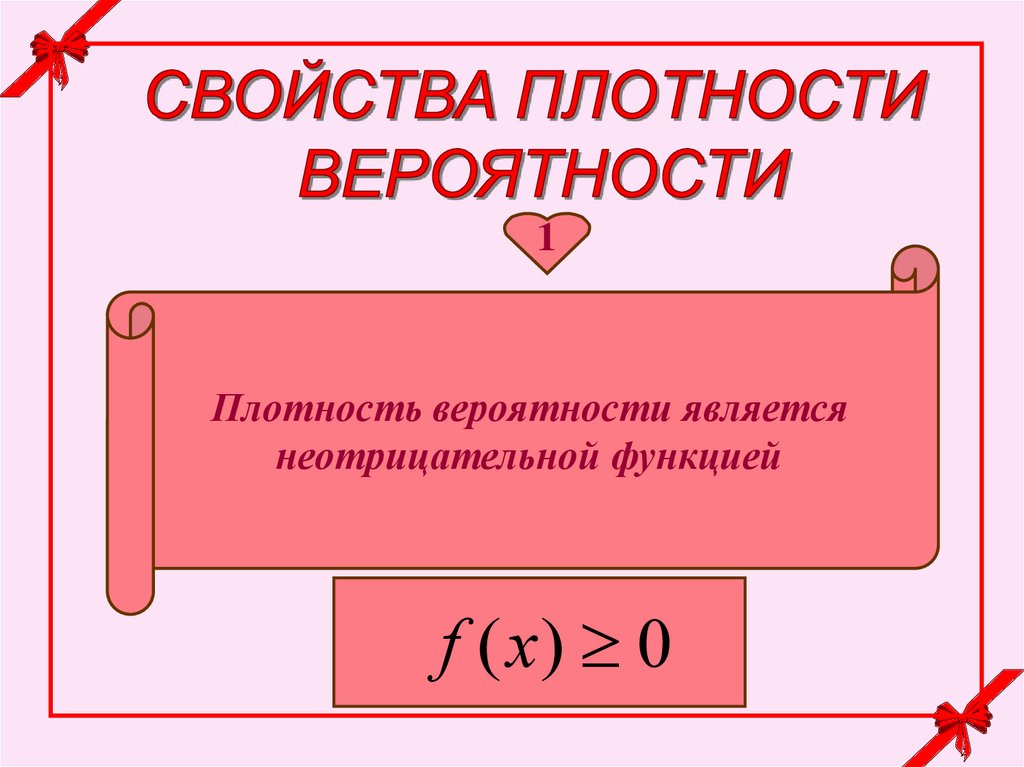
29.
1Плотность вероятности является
неотрицательной функцией
f ( x) 0
30.
2Вероятность попадания случайной величины
в отрезок
p ( X ) f ( x)dx
31.
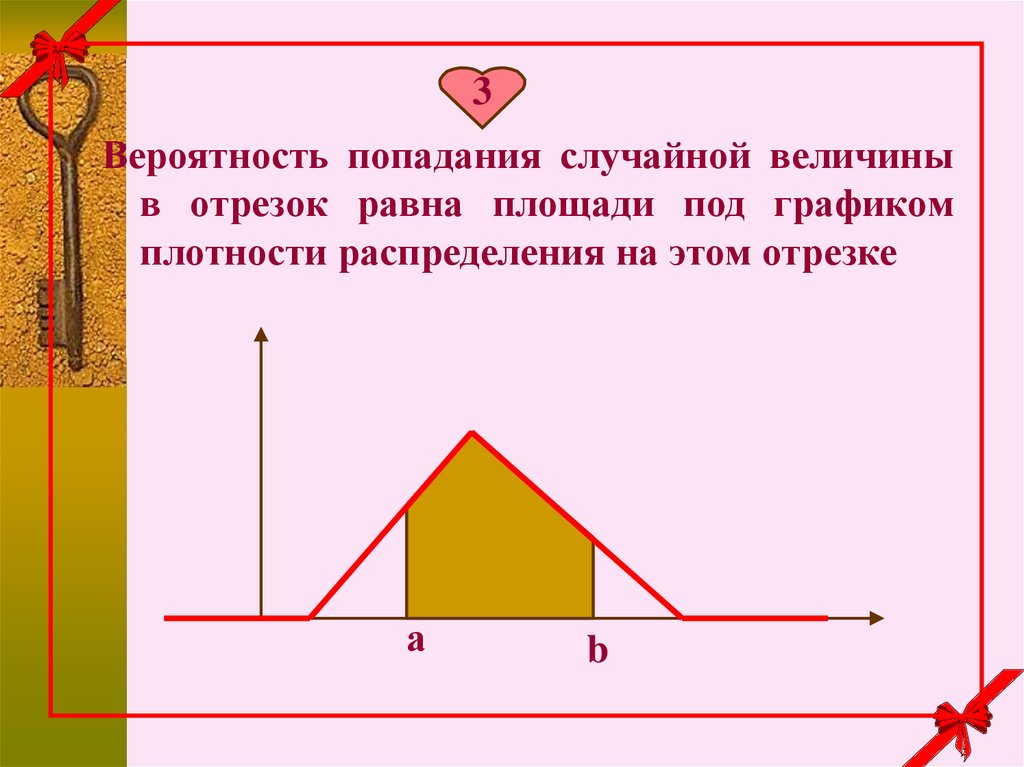
3Вероятность попадания случайной величины
в отрезок равна площади под графиком
плотности распределения на этом отрезке
а
b
32.
4Интеграл в бесконечных пределах
от плотности вероятности равен 1:
f ( x ) dx 1







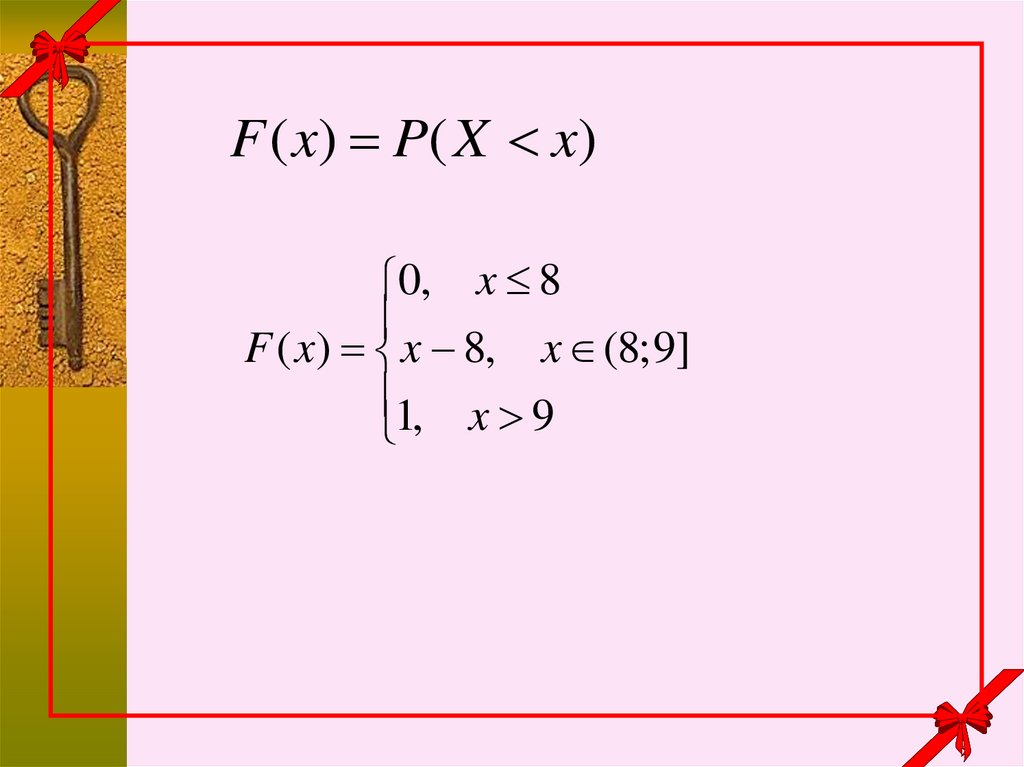



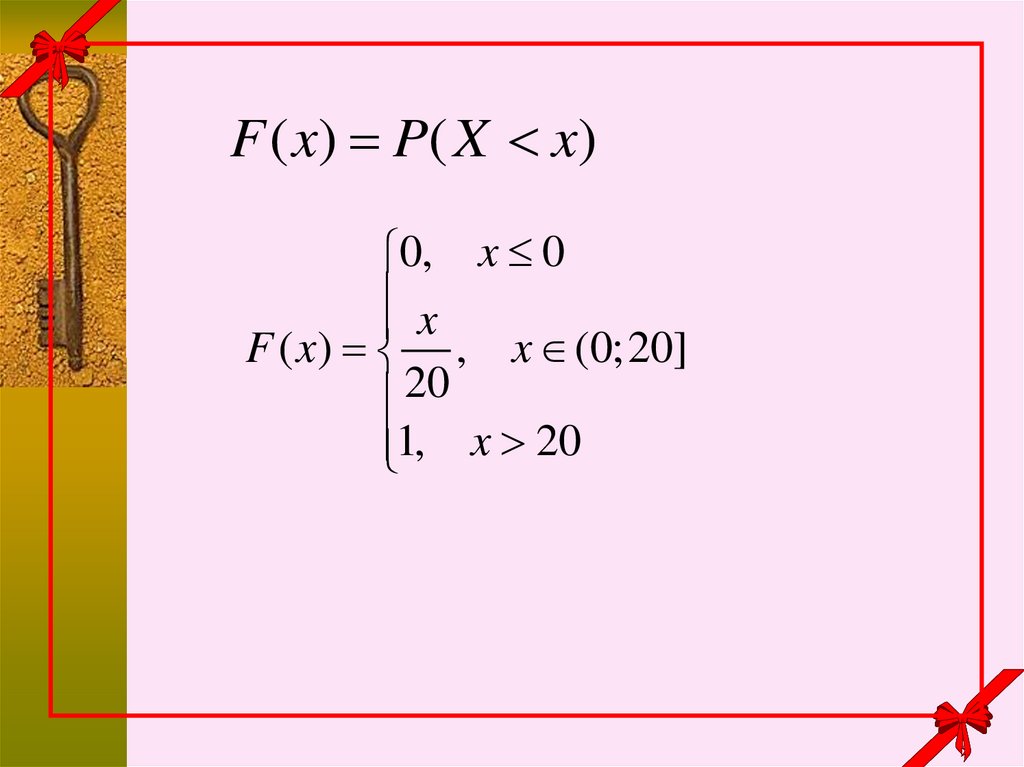




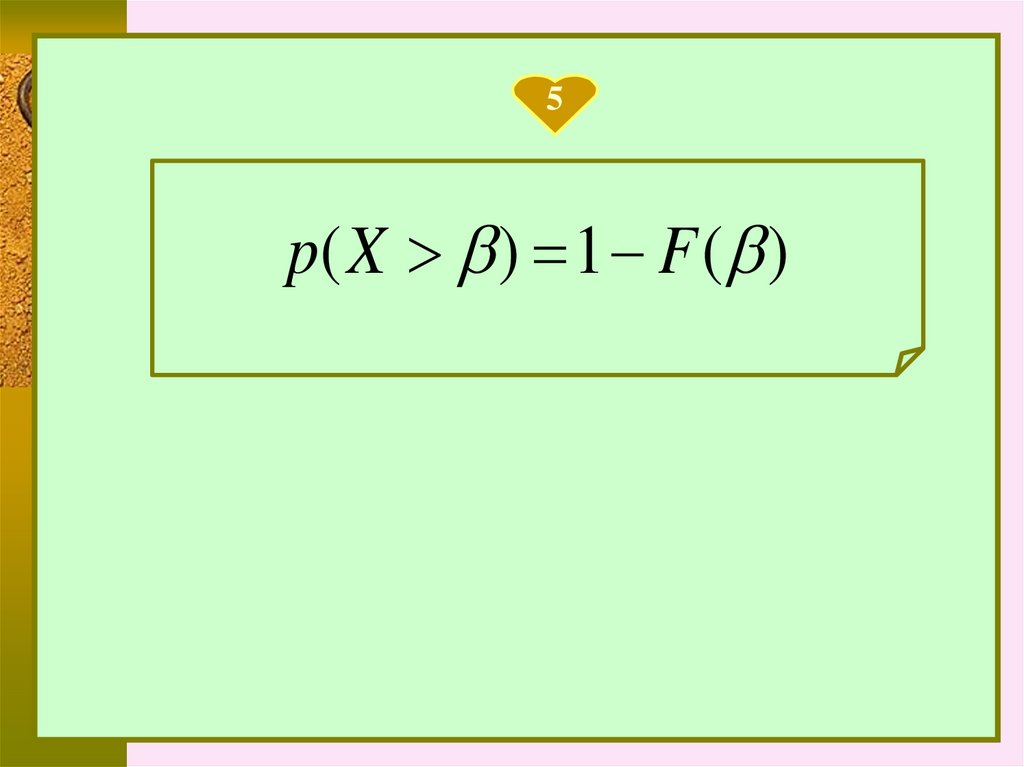









 Математика
Математика








