Похожие презентации:
Непрерывная случайная величина
1. Непрерывные случайные величины
Лекция 152. Непрерывные случайные величины
Случайные величины, возможные значениякоторых непрерывно заполняют некоторый
промежуток
Примеры:
- артериальное давление пациента;
- масса тела пациента;
- скорость биохимической реакции в клетке.
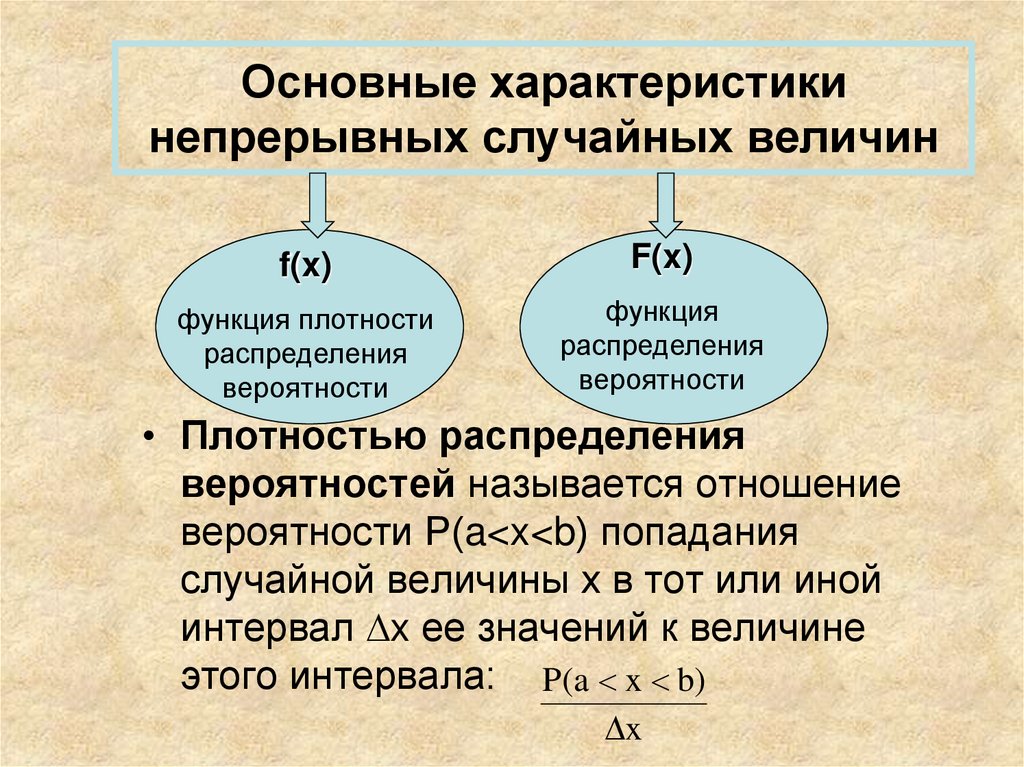
3. Основные характеристики непрерывных случайных величин
f(x)F(x)
функция плотности
распределения
вероятности
функция
распределения
вероятности
• Плотностью распределения
вероятностей называется отношение
вероятности Р(a<x<b) попадания
случайной величины x в тот или иной
интервал x ее значений к величине
этого интервала: P(a x b)
x
4.
• Функция плотности распределениявероятностей – это зависимость
плотности
распределения
от
значений величины x.
Функция плотности распределения вероятностей
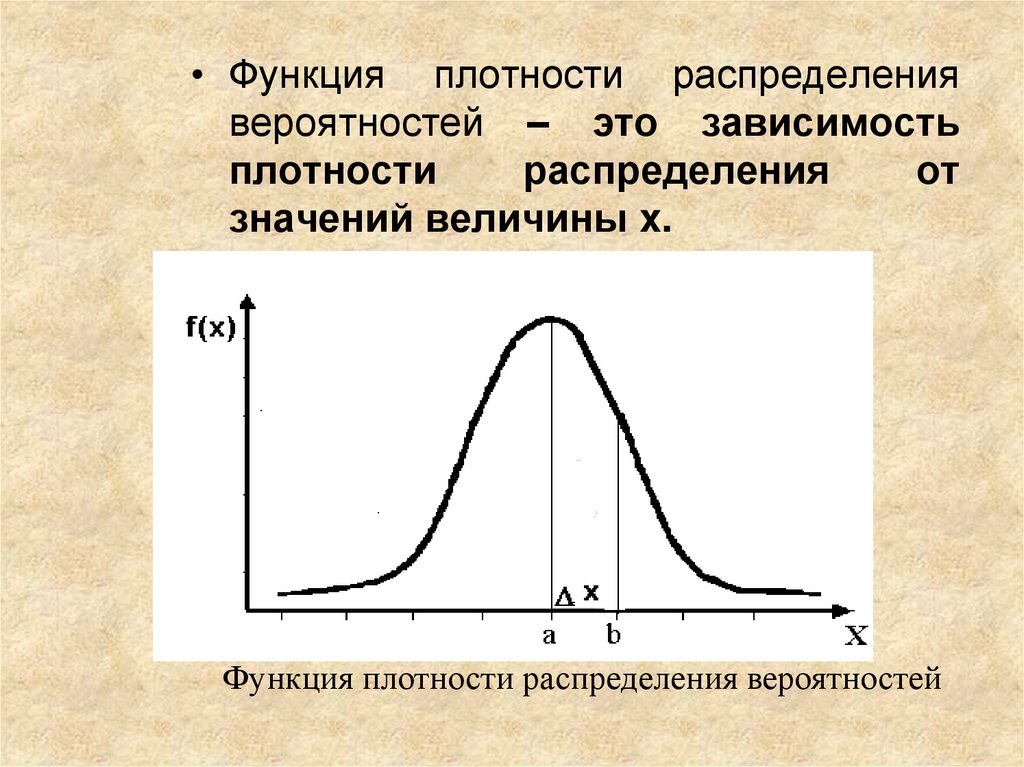
5. Пример: Функция плотности распределения вероятностей частоты пульса у студентов 1 курса КрасГМУ
Непрерывное распределениеf ( x)dx 1
условие
нормировки
1
f ( x)
e
10 2
x 69 2
200
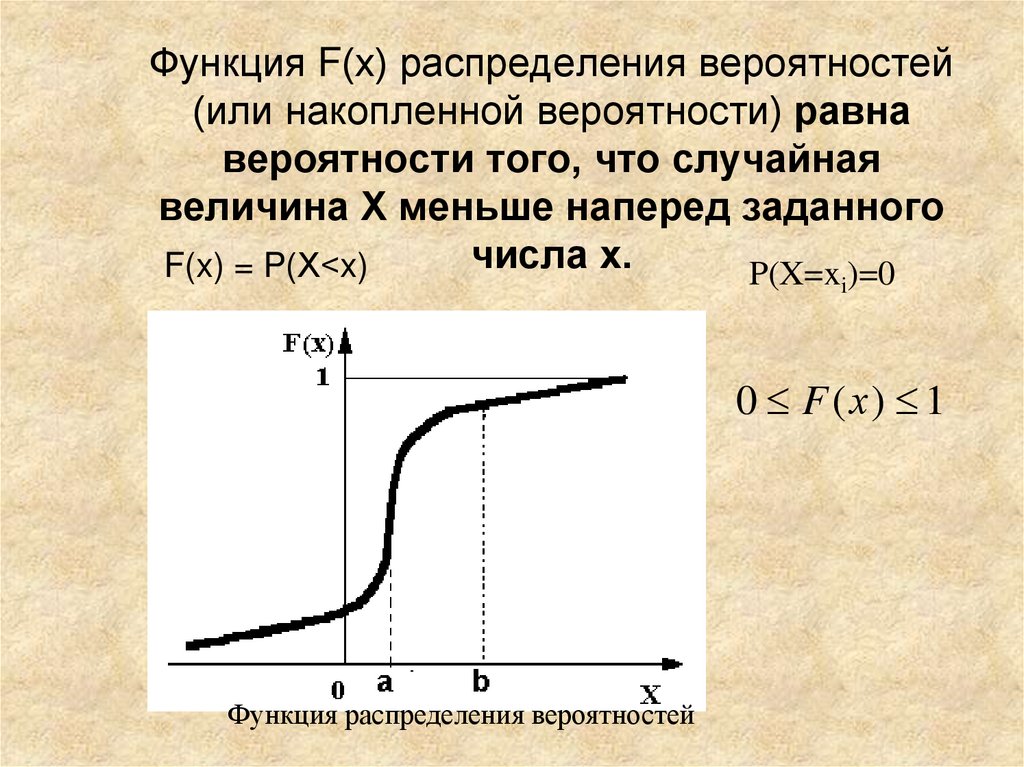
6. Функция F(х) распределения вероятностей (или накопленной вероятности) равна вероятности того, что случайная величина Х меньше
наперед заданногочисла x.
F(x) = P(Х<x)
P(X=x )=0
i
0 F ( х) 1
Функция распределения вероятностей
7. Вероятность попадания случайной величины на заданный участок
Задача: вычислить вероятность того, что случайнаявеличина примет значение , заключенное в некоторых
пределах, например, от a до b
a X b
Выразим вероятность этого события через функцию
распределения F(X):
Событие А: X < b;
Событие В: X < a
Событие С: a X < b
A=B+C
8. Вероятность попадания случайной величины на заданный участок-2
По теореме сложения вероятностей получим:P ( X b ) P ( X a ) P (a X b )
F (b ) F (a ) P (a X b )
P (a X b ) F (b ) F (a )
Вероятность попадания случайной величины на заданный
участок равна приращению функции распределения на
этом участке
9. Плотность распределения случайной величины
Вероятность попадания случайной величины на участок от х до х+ хP ( x X x x ) F ( x x ) F ( x )
F ( x x ) F ( x )
F ( x ) f ( x )
x 0
x
lim
f(x) – плотность функции распределения - производная
функции распределения – характеризует плотность, с
которой распределяется значение случайной величины в
данной точке
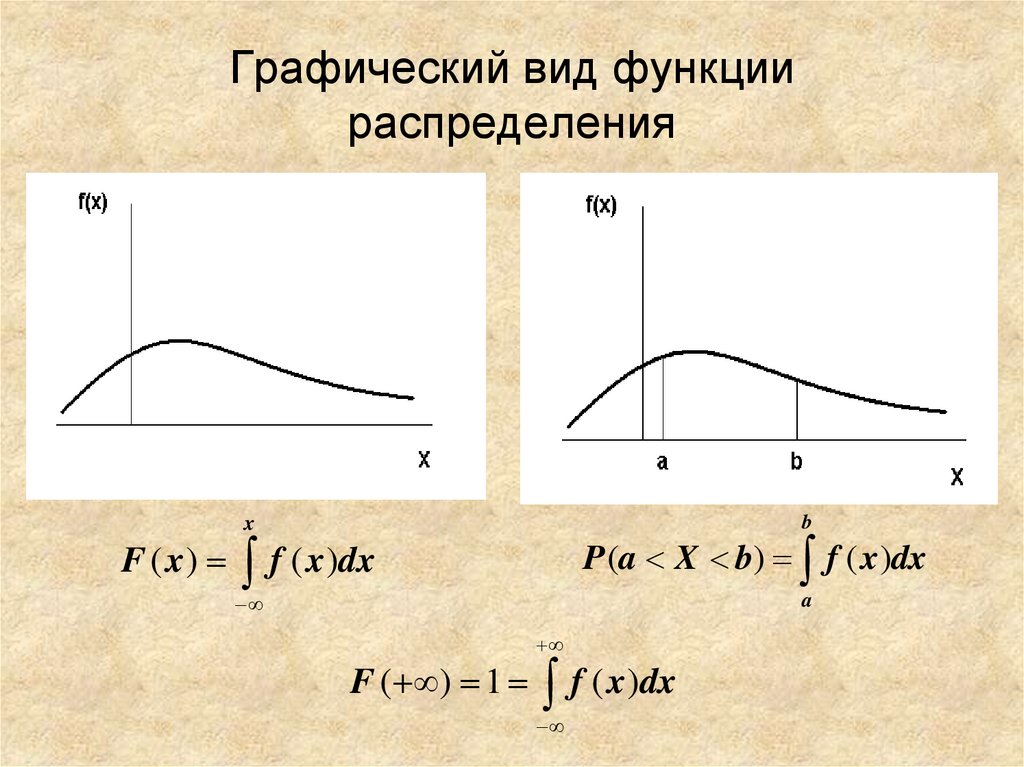
10. Графический вид функции распределения
bx
F ( x)
P (a X b) f ( x)dx
f ( x)dx
a
F ( ) 1
f ( x)dx
11. Связь между f(x) и F(x)
F(х) – является первообразной для f(х):b
F(x)=Р(a<x<b)= f ( x )dx
a F(a)
= F(b) –
f(x)=F′(x)
f(x)-дифференциальная функция
распределения
F(x)-интегральная функция
распределения
12. Задача
0, x 02
F ( x) x , 0 x 1
1, x 1
f ( x) ?
0, x 0
f ( x ) 2 x, 0 x 1
0, x 1
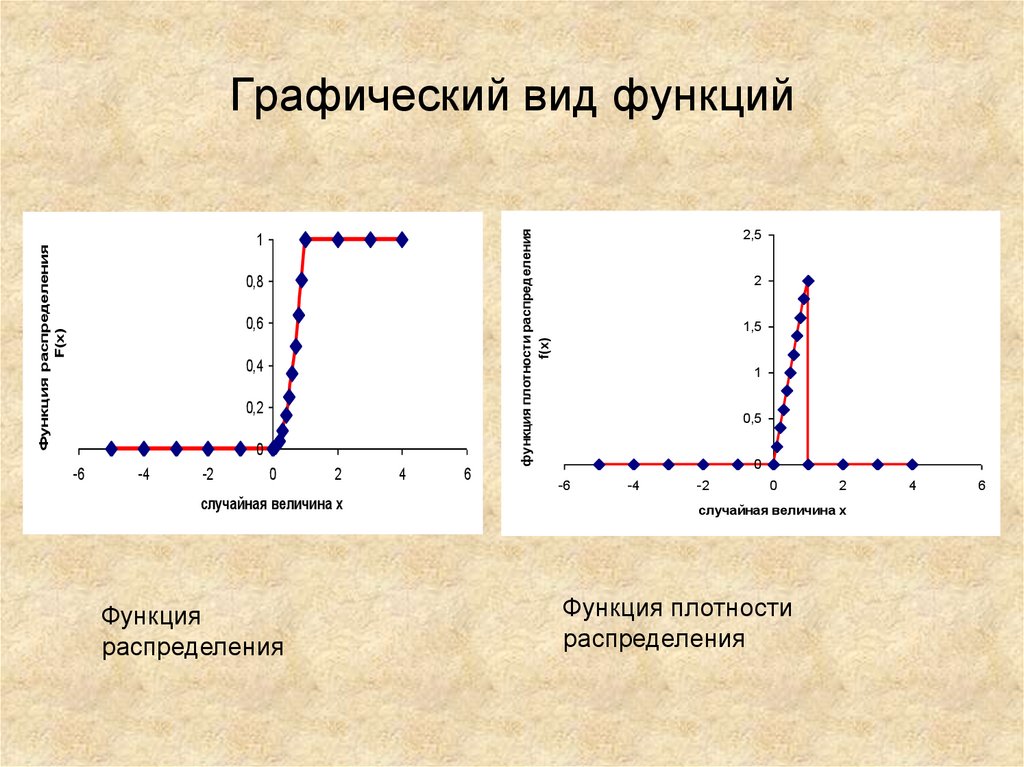
13. Графический вид функций
0,80,6
0,4
0,2
0
-6
-4
-2
0
2
случайная величина х
Функция
распределения
4
6
2,5
функция плотности распределения
f(x)
Функция распределения
F(x)
1
2
1,5
1
0,5
0
-6
-4
-2
0
2
случайная величина х
Функция плотности
распределения
4
6
14. Примеры:
Задана функция распределения
вероятностей непрерывной
случайной величины:
0 ïðè õ 0
cx 2
F(X )
ïðè 0 õ 2
4
1 ïðè õ 2
Найти: а)значение с, б)функцию плотности распределения
вероятностей f(Х), в) вероятность попадания случайной
величины Х в интервал (0;1). Построить графики функций
F(Х) и f(Х).
15. Решение:
• Константу С находим из условия :c x2
1 ïðè x 2
4
f (X )
c 22
1 , ñëåäîâàòåëüíî ñ 1
4
0 при х 0
x
при 0 х 2
2
0 при х 2
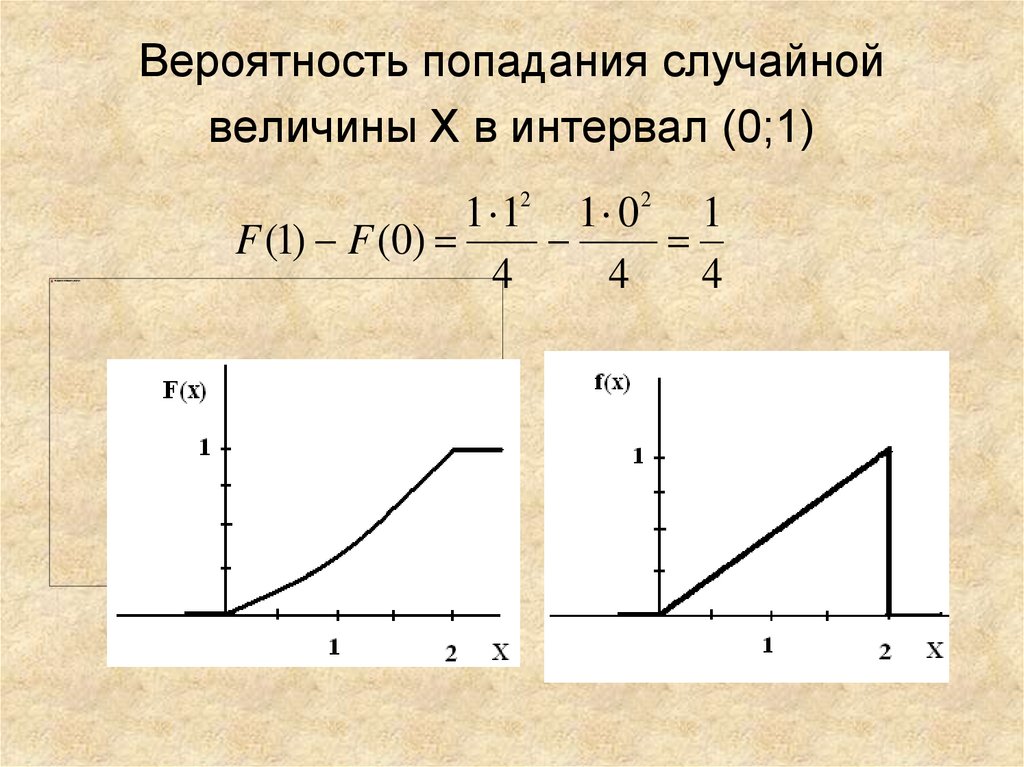
16. Вероятность попадания случайной величины Х в интервал (0;1)
1 12 1 0 2 1F (1) F (0)
4
4
4
17. Основные числовые характеристики непрерывных случайных величин
• Математическое ожиданиеМ ( х ) x f ( x )dx
• Дисперсия
Ì ( õ) x f ( x)dx
a
b
D( х )
b
( x M ( x))
2
f ( x )dx
D( õ) ( x M ( x)) 2 f ( x)dx
a
• Среднее квадратическое отклонение
( х) D( х)
18.
23
x
x
М ( х) x dx
2
6
0
2
0
3
2
4
6 3
4 2 x
16 x
2 8
D( х) ( x ) dx x x dx
3 2
3
9 2
0
0
2
2
x3 4 2 8
2 4 4 23 4 2 2 2
0 2 3 x 9 x dx 8 9 9 9
2
2
( х ) D( х )
0,47
9
19. Свойства математического ожидания
• Математическое ожидание постоянной величины Сравно этой постоянной: М(С)=С
• Постоянный множитель можно выносить за знак
математического ожидания: М(СХ)=СМ(Х)
• Математическое ожидание алгебраической суммы
случайных величин равно алгебраической сумме их
математических ожиданий: M(X Y)=M(X) M(Y)
• Математическое ожидание произведения случайных
величин равно произведению их математических
ожиданий: M(XY)=M(X)∙M(Y)
20. Свойства дисперсии случайной величины
• Дисперсия постоянной величины С равна нулю:D(C)=0
• Постоянный множитель можно выносить за знак
дисперсии возводя его в квадрат: D(CX)=C2D(X)
• Дисперсия двух случайных величин равна сумме
дисперсий этих величин: D(X+Y)=D(X)+D(Y)
• Дисперсия разности двух случайных величин равна
сумме дисперсий этих величин:
D(X-Y)=D(X)+D(Y)
21. Примеры:
Найти математическое ожидание
случайной величины Z=X+2Y, если
известно, что M(X)=4, M(Y)=2.
M(Z)=8
Найти дисперсию случайной величины
D(2X), если D(X)=10.
D(2X)=22 10=40
Найти дисперсию случайной величины
D(X-Y), D(2X+3), если D(X)=5, D(Y)=3.
D(X-Y)=5+3=8, D(2X+Y)= 22 5+ 0=20










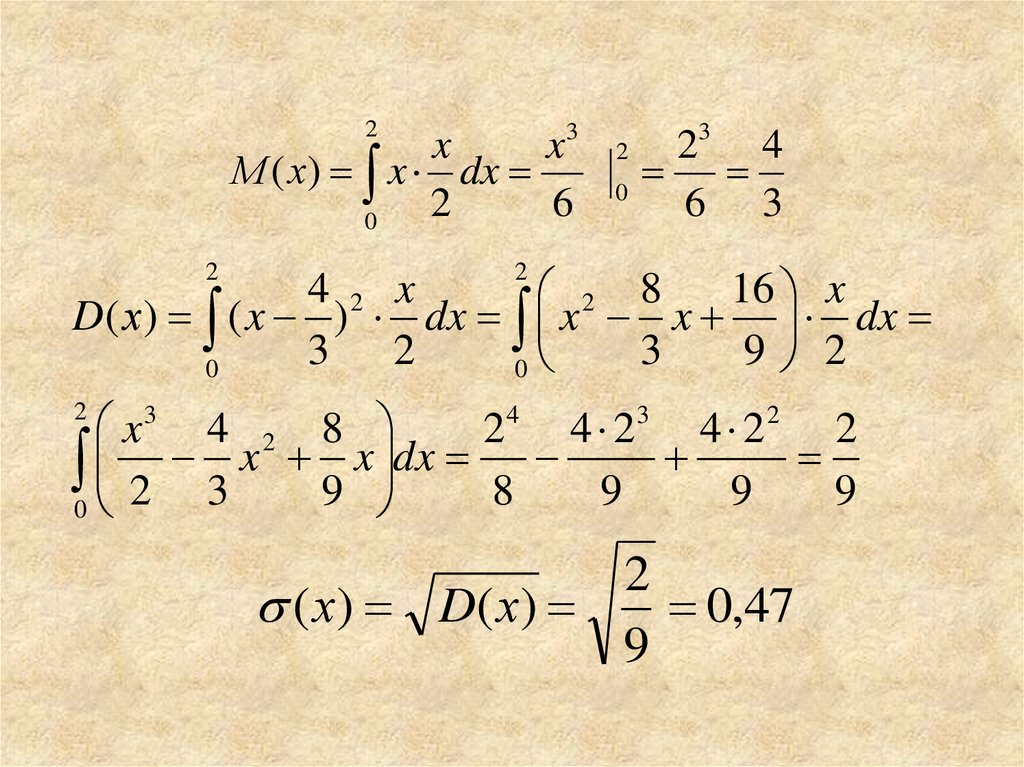



 Математика
Математика