Похожие презентации:
Representation of data in computer systems
1.
Representation ofdata in computer
systems
2.
Purpose: The concept of number systems, typesof number systems. Number systems used in
computers. Algorithms for converting numbers
from the binary number system to the octal,
hexadecimal number systems and back. Binary
arithmetic.
3.
Number system is a set of rules and methods ofrecording numbers by means of digits and symbols.
Number systems
positional
non-positional
Arabic (decimal)
unary (unit)
with the base of N
rome numbers
4. Arabic number system
Arabic number system ispositional decimal number
system.
This number system is used in
modern mathematics.
The basis of decimal
system is equal to 10.
The alphabet consists of 10
digits:
0123456789
In positional notation the value of each digit defines by its position in
number.
Any decimal number is represented as:
765=700+60+5=7*100+6*10+5*1=7*102 +6*101 +5*100
or
76,54=7*10+6*1+5*0,1+4*0,01=7*102+6*101+5*10-1+4*10-2
5. Number systems with the basis of N
Number systemBase
Alphabet of digits
N=2
Binary
2
01
N=8
Octal
8
01234567
N=10
Decimal
10
0123456789
N=16
Hexadecimal
16
0123456789
ABCDEF
In computers the binary number system is used. Also octal and
hexadecimal systems are used by programmers
6. Converting numbers to decimal system
To convert numbers from binary (octal, hexadecimal)system to decimal it’s necessary to represent them as
sum of basis powers of given system.
76543210
101001102=1*27+0*26+1*25+0*24+0*23+1*22+
+1*21+0*20=128+32+4+2=16610
210
7038=7*82+0*81+3*80=448+3=44710
43210
23FA116=2*164+3*163+15*162+10*161+1*160=
131072+12288+3840+160+1=14736110
7. Converting numbers from decimal system
With this aim we should divide the given number bythe basis of system to which we are going to convert it
until we get the remainder less than the basis. Received
remainders are digits which we’ll use for record
number in reversed sequence (from below to up)
2610=110102
24110=3618
362710=E2B16
8. Converting numbers from binary system
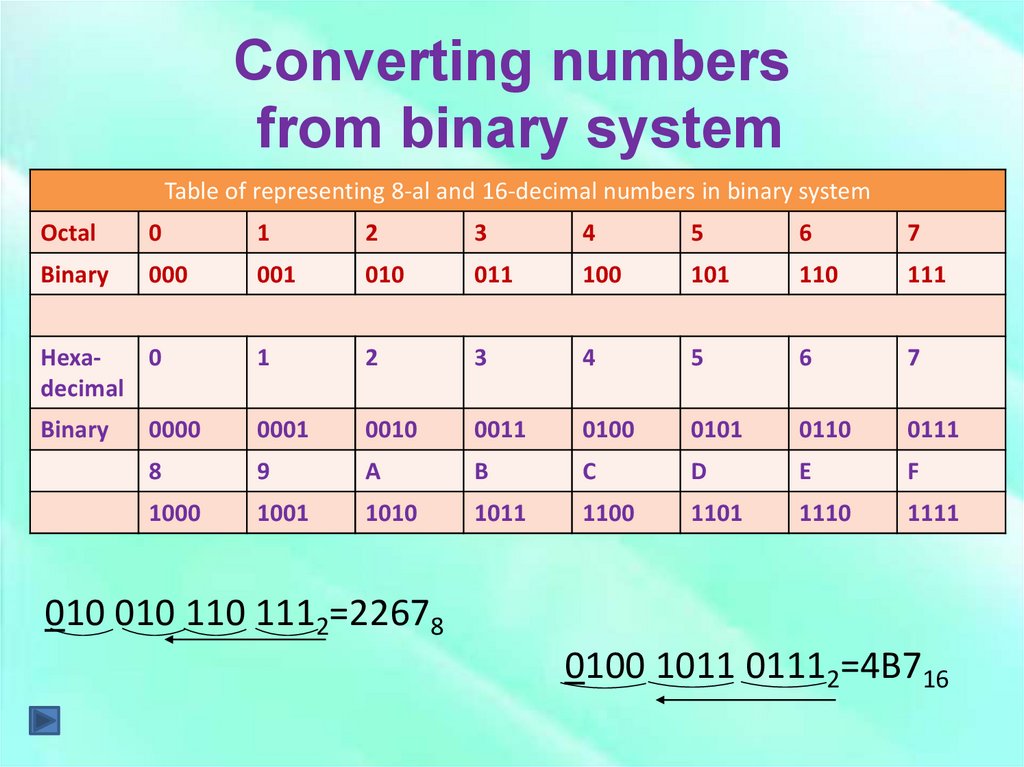
Table of representing 8-al and 16-decimal numbers in binary systemOctal
0
1
2
3
4
5
6
7
Binary
000
001
010
011
100
101
110
111
Hexa0
decimal
1
2
3
4
5
6
7
Binary
0000
0001
0010
0011
0100
0101
0110
0111
8
9
A
B
C
D
E
F
1000
1001
1010
1011
1100
1101
1110
1111
010 010 110 1112=22678
0100 1011 01112=4В716
9. Converting numbers to binary system
For converting octal (hexadecimal) numberto binary it is necessary to replace each
figure with a binary triad (tetrad)
equivalent to it
7268= 111 010 1102
74С16 = 0111 0100 11002
(at record of the number the first 0 isn’t written)
10. Converting numbers from 16-decimal to 8-al and vice versa
For converting from octal system tohexadecimal and vice versa it’s necessary
to use binary system
FAE16=1111101011102
111 110 101 1102=76568
6358 =1100111012
1 1001 11012=19D16
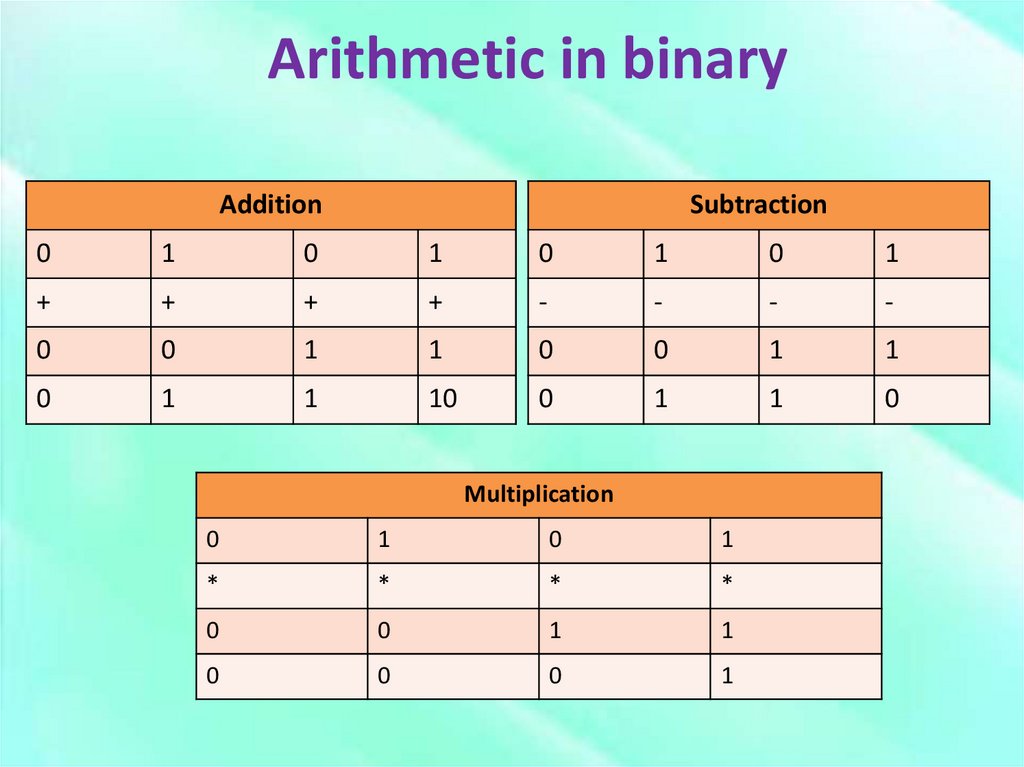
11. Arithmetic in binary
AdditionSubtraction
0
1
0
1
0
1
0
1
+
+
+
+
-
-
-
-
0
0
1
1
0
0
1
1
0
1
1
10
0
1
1
0
Multiplication
0
1
0
1
*
*
*
*
0
0
1
1
0
0
0
1
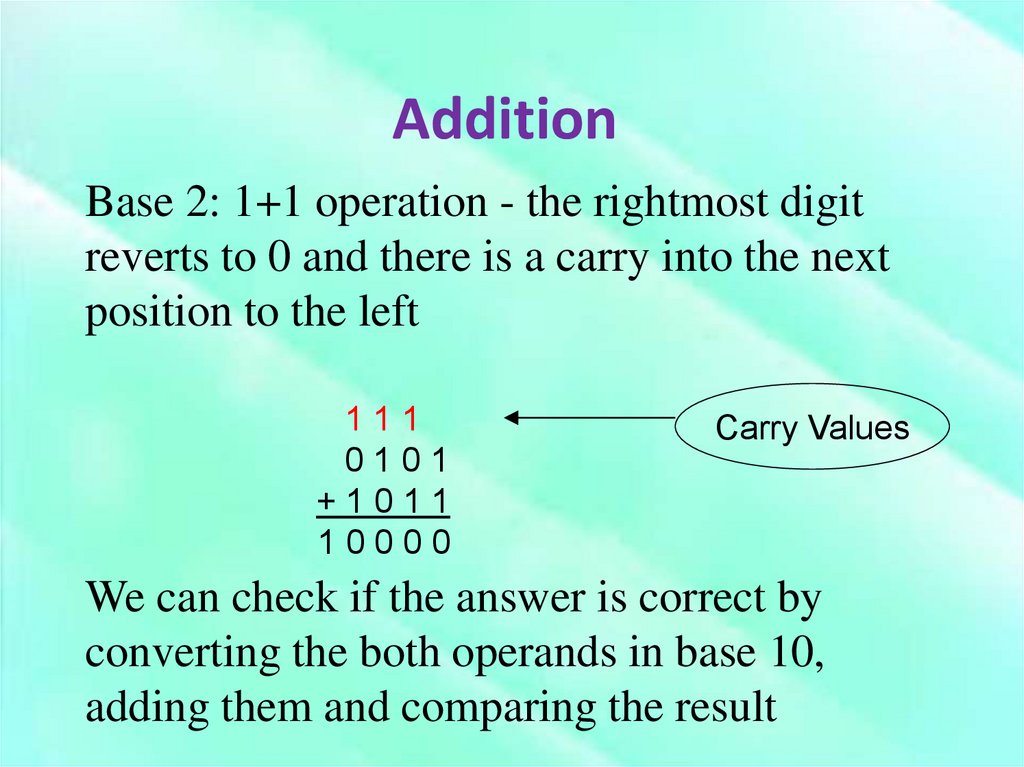
12. Addition
Base 2: 1+1 operation - the rightmost digitreverts to 0 and there is a carry into the next
position to the left
111
0101
+1011
10000
Carry Values
We can check if the answer is correct by
converting the both operands in base 10,
adding them and comparing the result
13. Subtracting
• The rules of the decimal base applies to binaryas well. To be able to calculus 0-1, we have to
“borrow one” from the next left digit.
• More precisely, we have to borrow one power
of the base
1 10 10
1010
-0111
0011
Borrow Values
• You can check if the result is correct by
converting the operands in decimal and
making the calculus.
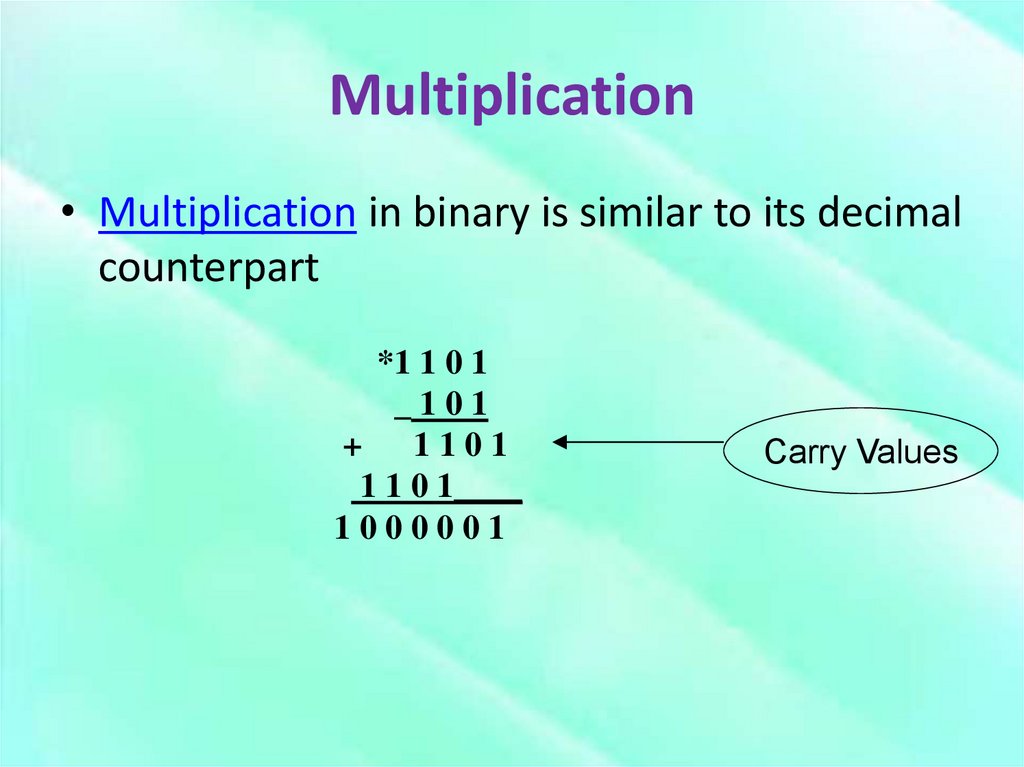
14. Multiplication
• Multiplication in binary is similar to its decimalcounterpart
*1 1 0 1
_101
+
1101
1 1 0 1____
1000001
Carry Values










 Информатика
Информатика








