Представление чисел в памяти ЭВМ (Лекция 03)

1.

МАТЕМАТИЧЕСКИЕ
ОСНОВЫ
ИНФОРМАТИКИ
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В
ПАМЯТИ ЭВМ

2.

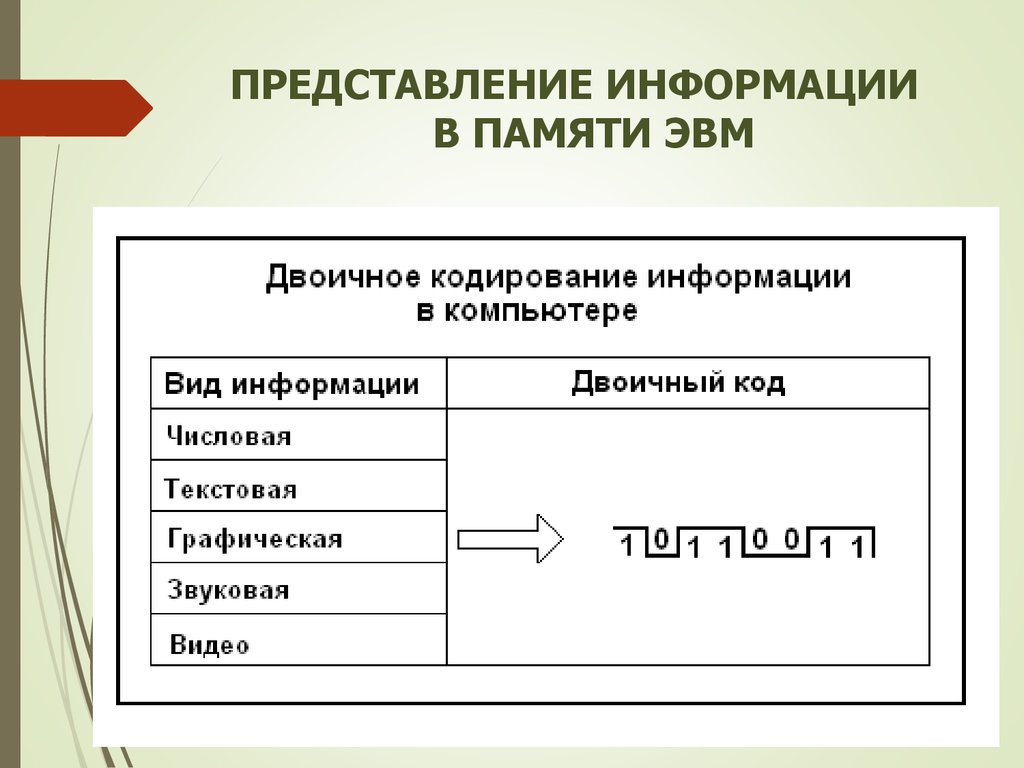
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ
В ПАМЯТИ ЭВМ
Для представления информации в памяти ЭВМ (как
числовой, так и не числовой) используется двоичный
способ кодирования.
Информация в компьютере представлена в двоичном коде,
алфавит которого состоит из двух цифр (0 и 1).
Элементарная ячейка памяти ЭВМ имеет длину 8 бит
(1 байт). Каждый байт имеет свой номер (его
называют адресом).
Наибольшую последовательность бит, которую ЭВМ может
обрабатывать как единое целое, называют машинным
словом. Длина машинного слова зависит от разрядности
процессора и может быть равной 16, 32, 64 битам и т.д.

3.

ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ
В ПАМЯТИ ЭВМ

4.

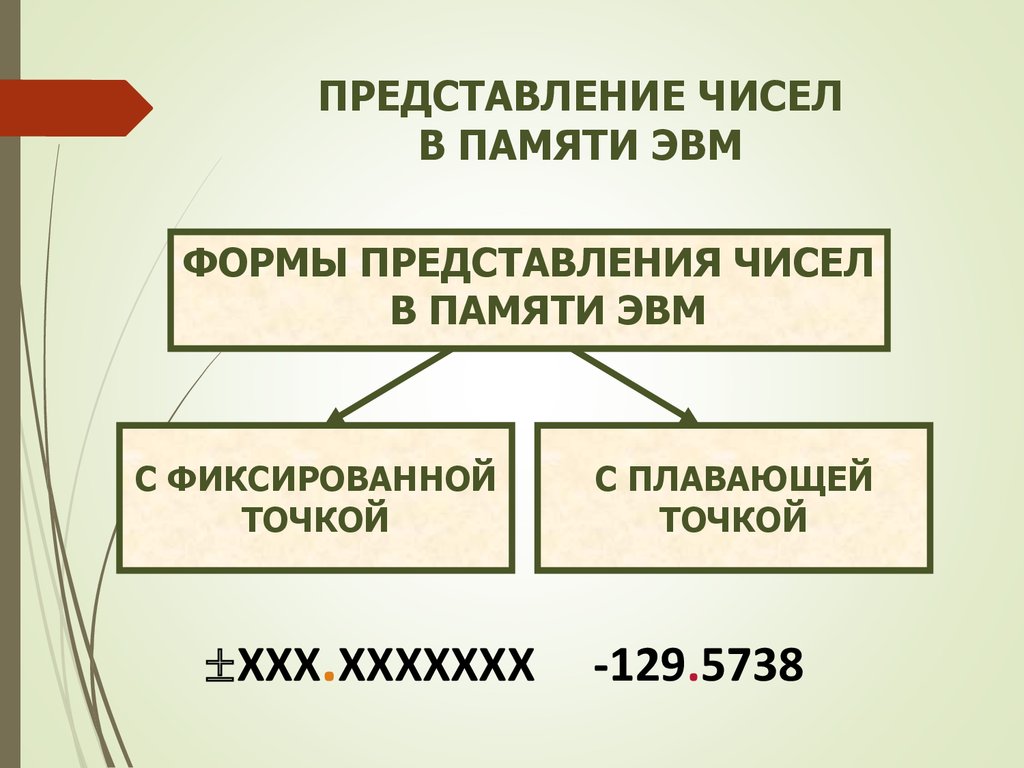
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ
В ПАМЯТИ ЭВМ
ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
В ПАМЯТИ ЭВМ
С ФИКСИРОВАННОЙ
ТОЧКОЙ
ХХХ.ХХХХХХХ
С ПЛАВАЮЩЕЙ
ТОЧКОЙ
-129.5738

5. ПРЕДСТАВЛЕНИЕ С ФИКСИРОВАННОЙ ТОЧКОЙ

0V1
В современных компьютерах представление
с фиксированной точкой используется для целых
чисел

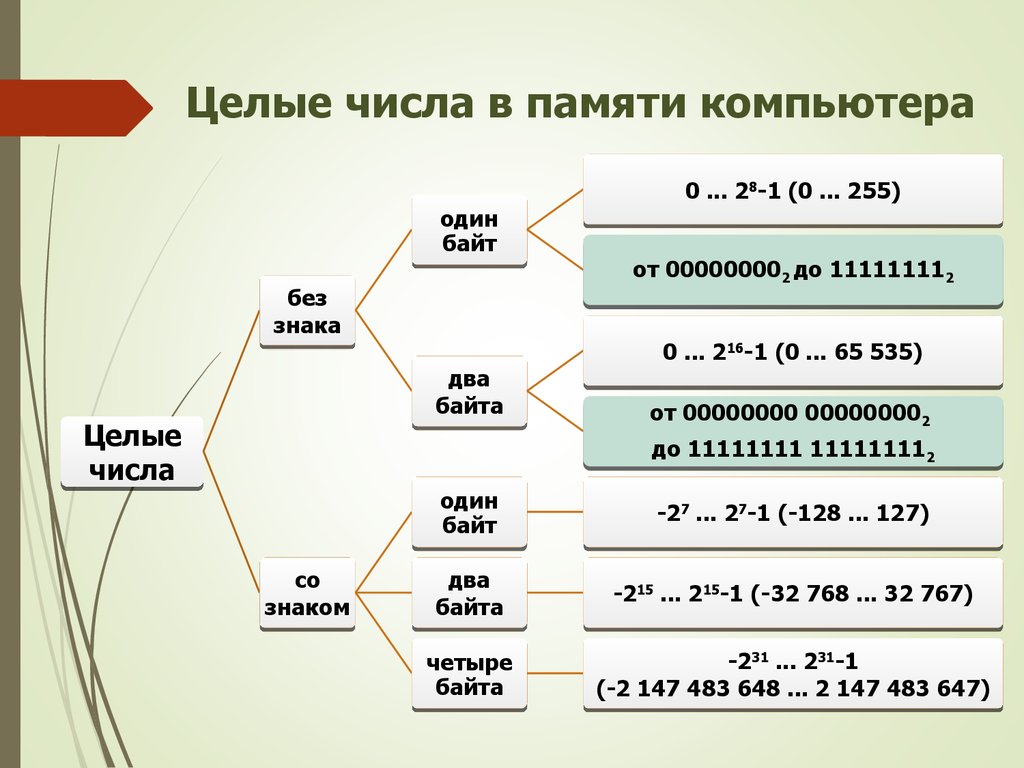
6. Целые числа в памяти компьютера

один
байт
без
знака
два
байта
Целые
числа
со
знаком
0 ... 288-1 (0 ... 255)
от 0000000022 до 1111111122
16-1 (0 ... 65 535)
0 ... 216
от 00000000 0000000022
до 11111111 1111111122
один
байт
-277 ... 277-1 (-128 ... 127)
два
байта
15 ... 215
15-1 (-32 768 ... 32 767)
-215
четыре
байта
31 ... 231
31-1
-231
(-2 147 483 648 ... 2 147 483 647)

7. ЦЕЛЫЕ ЧИСЛА БЕЗ ЗНАКА

Максимальное число:
во всех разрядах единицы
Диапазон n-разрядного числа: 0 (2n-1)
Диапазон числа
Длина числа Запись со
в байтах
степенью Обычная запись
двойки
1
2
4
0 2 8 -1
0 2 16 -1
0 2 32 -1
0 255
0 65 535
0 4 294 967 295

8. ЦЕЛЫЕ ЧИСЛА БЕЗ ЗНАКА

Пример. (72)10=(1001000)2

9. ЧИСЛА БЕЗ ЗНАКА

Число 3910 = 100111 2 в однобайтовом формате:
Номера разрядов
7
6
5
4
3
2
1
0
Биты числа 0 0 1 0 0 1 1 1
Число 3910 = 100111 2 в двубайтовом формате:
Номера разрядов
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Биты числа 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1
Число 65 53510 = 11111111 111111112 в двубайтовом формате:
Номера разрядов
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Биты числа 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

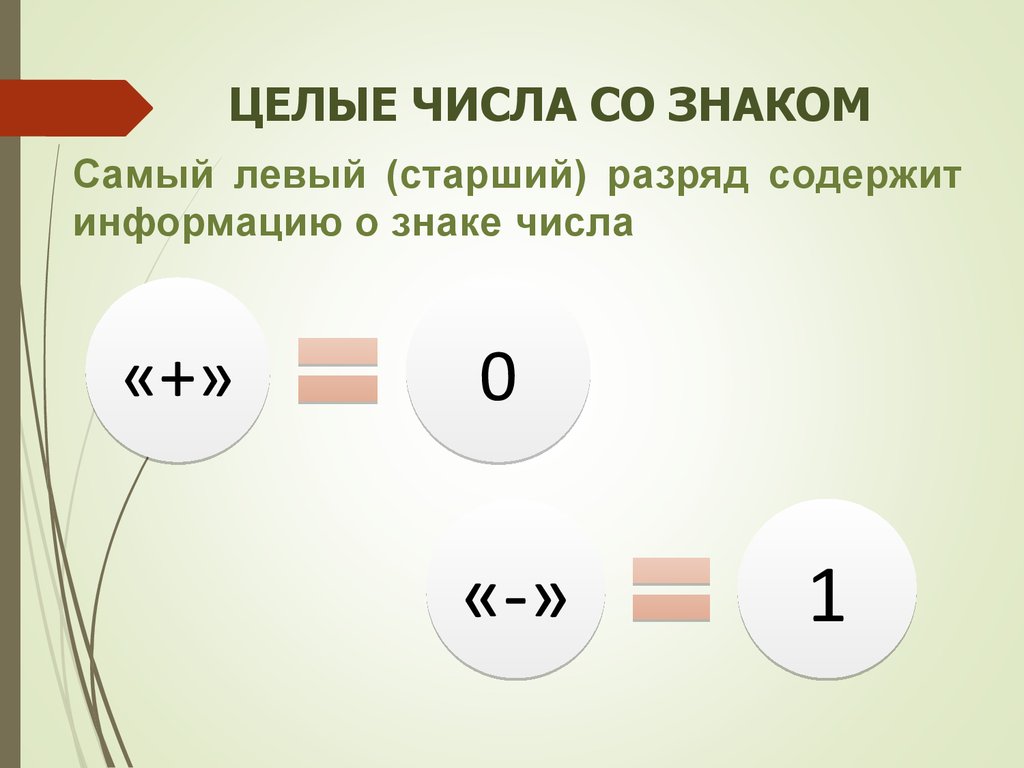
10. ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ

Самый левый (старший) разряд содержит
информацию о знаке числа
«+»
0
«-»
1

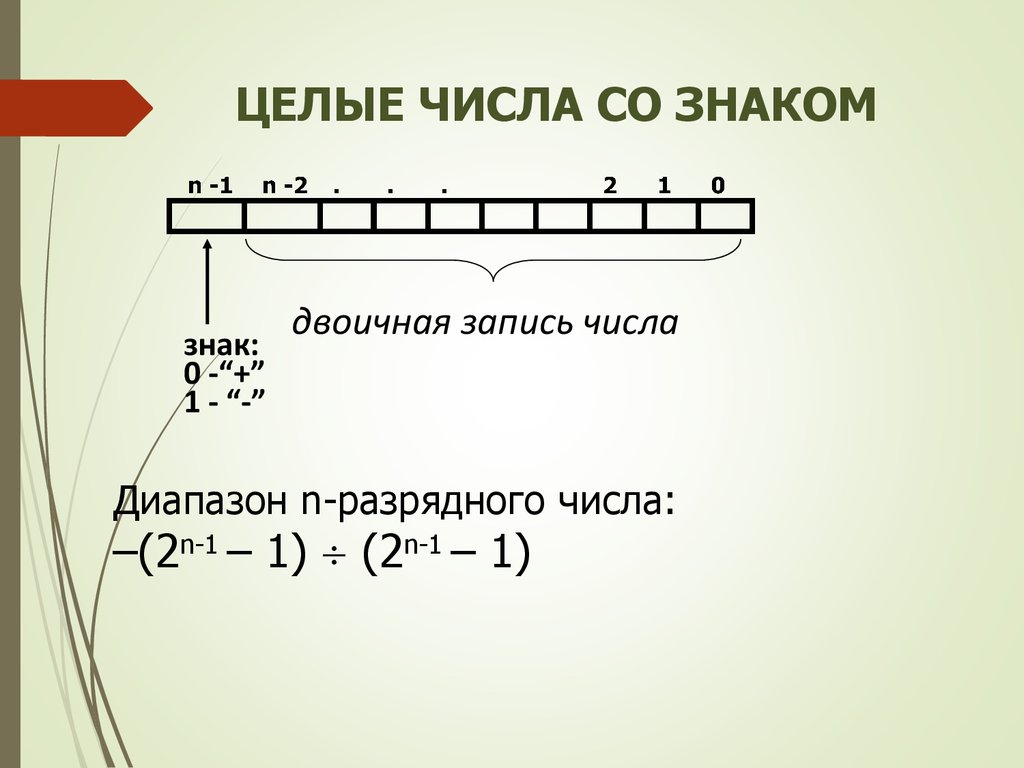
11. ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ

знак:
0 -“+”
1 - “-”
двоичная запись числа
Диапазон n-разрядного числа:
–(2n-1 – 1) (2n-1 – 1)

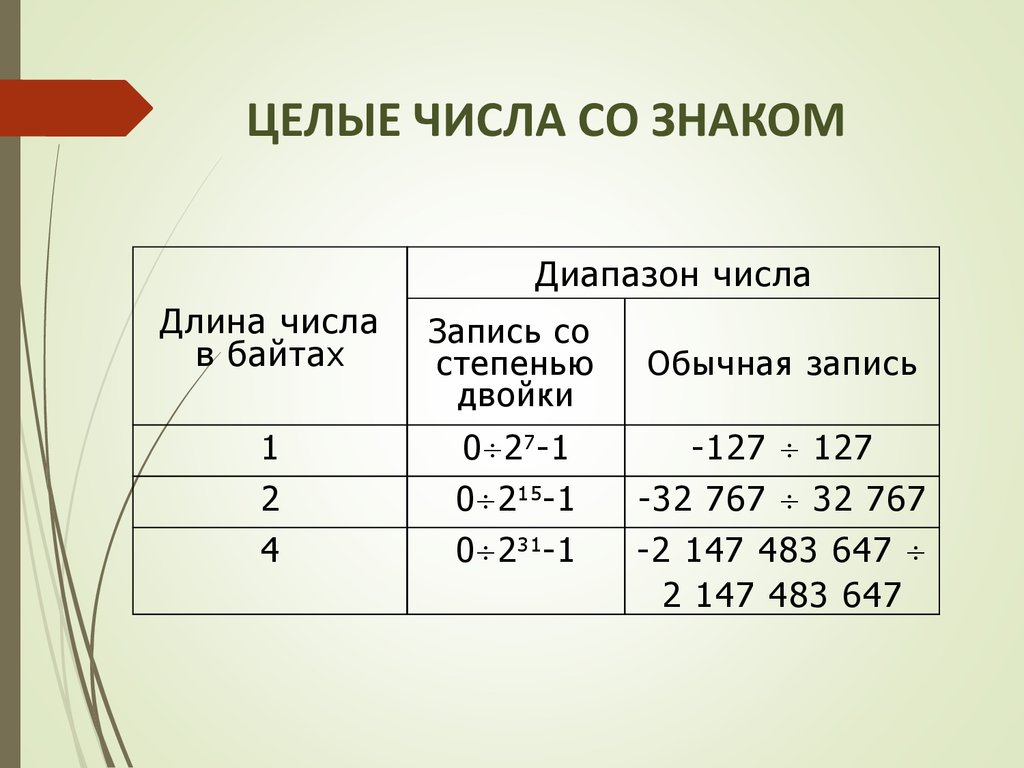
12.

ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ
Диапазон числа
Длина числа
в байтах
Запись со
степенью
двойки
Обычная запись
1
0 2 7 -1
-127 127
2
4
0 2 15 -1
0 2 31 -1
-32 767 32 767
-2 147 483 647
2 147 483 647

13. ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ

В ЭВМ в целях упрощения выполнения
арифметических операций применяют
специальные коды для представления целых чисел.
Прямой код числа
Обратный код числа
Дополнительный код числа

14.

ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ
СО ЗНАКОМ
Разряды числа в коде жестко связаны с разрядной
сеткой (8, 16, 32, 64 разряда);
Для записи кода знака числа в разрядной сетке
отводится фиксированный разряд.
Знаковым разрядом является старший разряд
в разрядной сетке.
знаковый разряд
0
7
1
1
0
1
0
0
1
0

15.

ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ
СО ЗНАКОМ
Прямой код двоичного числа
Прямой код двоичного числа совпадает по
изображению с записью самого числа.
Значение знакового разряда для положительных чисел
равно 0, а для отрицательных чисел равно 1.
+1101
0 0 0 0 1 1 0 1
-1101
1 0 0 0 1 1 0 1

16.

ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ
СО ЗНАКОМ
Обратный код двоичного числа
Обратный код для положительного числа совпадает с
прямым кодом.
Для отрицательного числа все цифры числа
заменяются на противоположные (1 на 0, 0 на 1), а в
знаковый разряд заносится единица.
+1101
-1101
0
0
0
0
1
1
0
1
- прямой код
0
0
0
0
1
1
0
1
- обратный код
1
0
0
0
1
1
0
1
- прямой код
1
1
1
1
0
0
1
0
- обратный код

17.

ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ
СО ЗНАКОМ
Дополнительный код положительного
двоичного числа
Дополнительный код для положительного числа
совпадает с прямым кодом.
+1101
Прямой код
00001101
Обратный код Дополнительный
код
00001101
00001101

18.

ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ
СО ЗНАКОМ
Дополнительный код отрицательного
двоичного числа
Для отрицательного числа дополнительный код
образуется путем получения обратного кода и
добавлением к младшему разряду единицы.
-1101
Прямой код Обратный код Дополнительный код
10001101
11110010
11110011

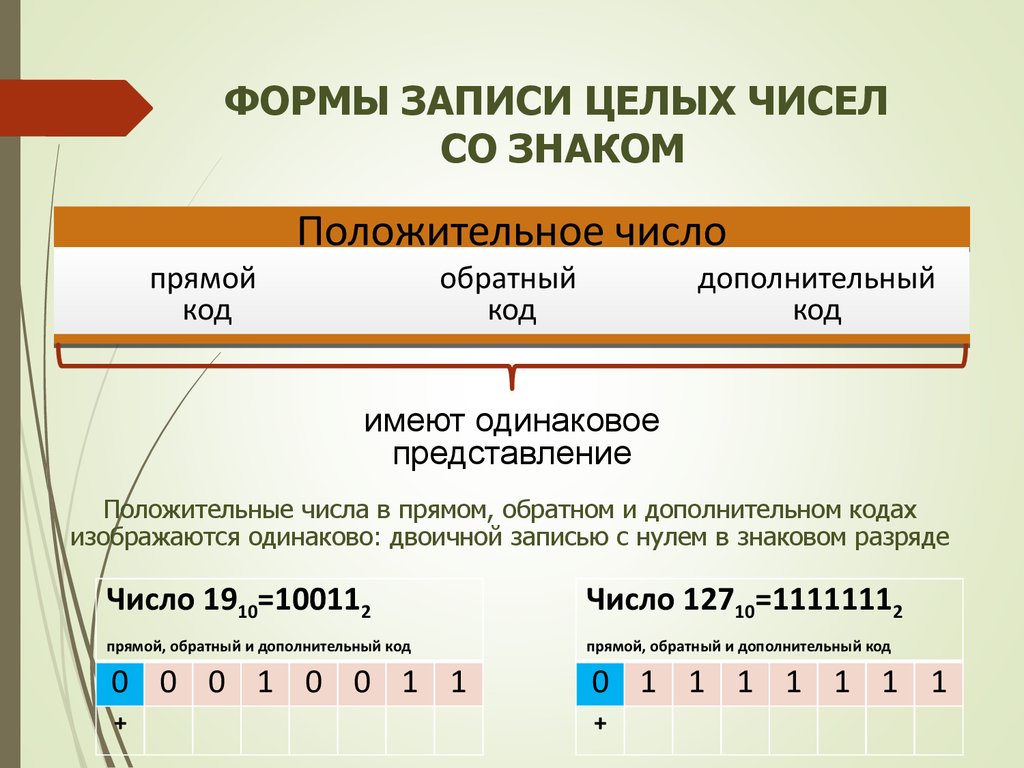
19. ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ

прямой
код
Положительное число
обратный
код
дополнительный
код
имеют одинаковое
представление
Положительные числа в прямом, обратном и дополнительном кодах
изображаются одинаково: двоичной записью с нулем в знаковом разряде
Число 1910=100112
Число 12710=11111112
прямой, обратный и дополнительный код
прямой, обратный и дополнительный код
0 0 0 1 0 0 1 1
0 1 1 1 1 1 1 1
+
+

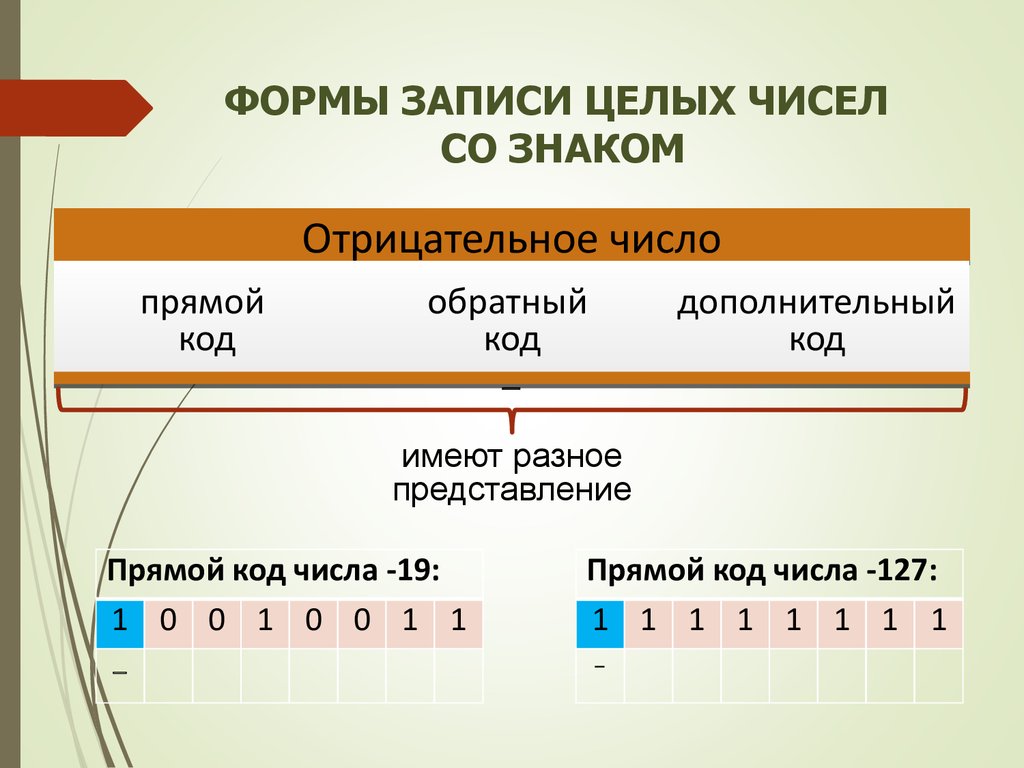
20. ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ

Отрицательное число
прямой
код
обратный
код
дополнительный
код
имеют разное
представление
Прямой код числа -19:
1 0 0 1 0 0 1 1
Прямой код числа -127:
1 1 1 1 1 1 1 1

21. ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ

Обратный код отрицательного числа получается
инвертированием всех цифр двоичного кода
абсолютной величины числа, включая разряд знака:
нули заменяются единицами, а единицы – нулями.
Число -19:
Код модуля числа:
Число -127:
0 0010011
Код модуля числа:
0 1111111
Обратный код числа: 1 1101100
Обратный код числа: 1 0000000
1 1 1 0 1 1 0 0
-
1 0 0 0 0 0 0 0
-

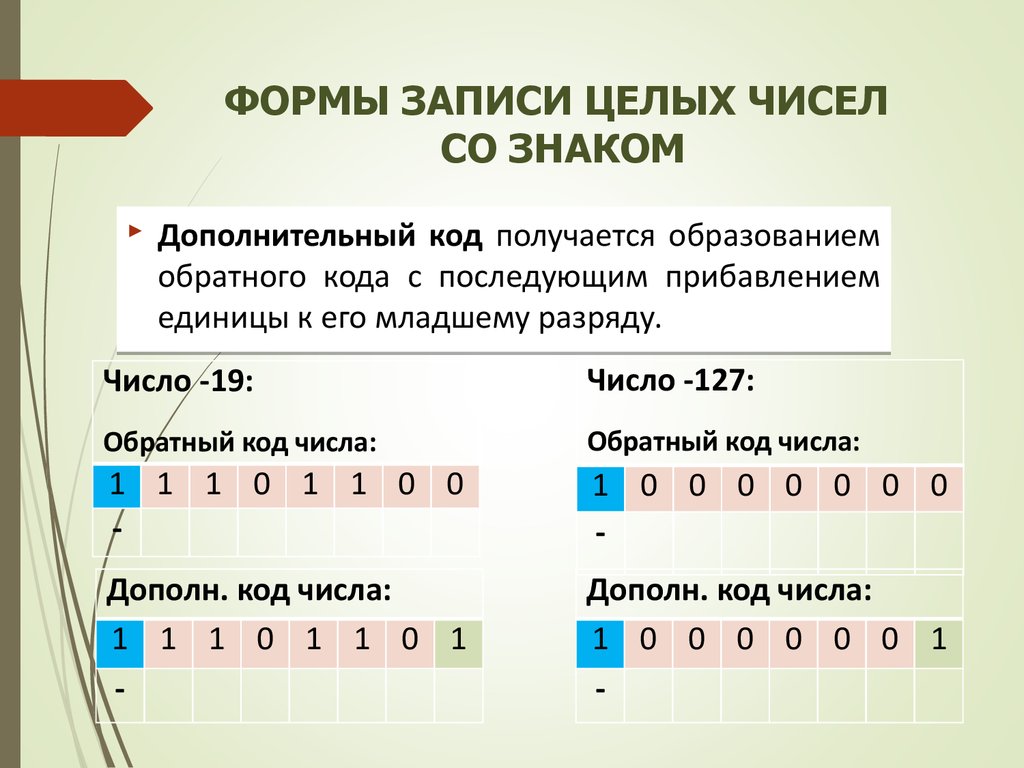
22. ФОРМЫ ЗАПИСИ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ

Дополнительный код получается образованием
обратного кода с последующим прибавлением
единицы к его младшему разряду.
Число -19:
Число -127:
Обратный код числа:
Обратный код числа:
1 1 1 0 1 1 0 0
-
1 0 0 0 0 0 0 0
-
Дополн. код числа:
1 1 1 0 1 1 0 1
-
Дополн. код числа:
1 0 0 0 0 0 0 1
-

23.

ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ
Применение
обратного
и
Применение обратного и
дополнительного
дополнительногокодов
кодовпозволяет
позволяет
упростить
упроститьконструкцию
конструкциюарифметикоарифметикологического
логическогоустройства
устройстваза
засчет
счетсведения
сведения
разнообразных
разнообразныхарифметических
арифметических
операций
операцийкксложению
сложению

24. Действия над двоичными кодами с фиксированной точкой

Вычитание заменяется сложением в
обратном или дополнительном коде;
Умножение сводится к сложению со
сдвигом в специальном регистре АЛУ накапливающем сумматоре;
Деление реализуется как многократное
прибавление к делимому
дополнительного кода делителя.

25. Арифметические действия

В большинстве компьютеров операция вычитания
не выполняется. Вместо неё производится
сложение уменьшаемого с обратным или
дополнительным кодом вычитаемого.
При сложении обратных и дополнительных кодов
чисел А и В в зависимости от знаков и соотношения
чисел имеют место различные случаи.

26. Арифметические действия

1) А и В положительные:
Десятичная запись:
+
Двоичные коды:
5
Апк
0 0 0 0 0 1 0 1
7
Впк
0 0 0 0 0 1 1 1
12
Спк
0 0 0 0 1 1 0 0
прямой код = обратный код = дополнительный код

27. Арифметические действия с обратными кодами

2) А – положительное, В – отрицательное, |B|>|A|
Десятичная запись:
+
Двоичные коды:
3
Апк
0 0 0 0 0 0 1 1
-10
Вок
1 1 1 1 0 1 0 1
-7
Сок
1 1 1 1 1 0 0 0

28. Арифметические действия с обратными кодами

3) А – положительное, В – отрицательное, |B|<|A|
Десятичная запись:
+
Двоичные коды:
10
Апк
0 0 0 0 1 0 1 0
-3
Вок
1 1 1 1 1 1 0 0
0 0 0 0 0 1 1 0
7
Сок
+ 1
0 0 0 0 0 1 1 1
Единицу переноса из знакового разряда компьютер
прибавляет к младшему разряду суммы для
корректировки результата.

29. Арифметические действия с обратными кодами

4) А и В – отрицательное
Десятичная запись:
+
Двоичные коды:
-3
Аок
1 1 1 1 1 1 0 0
-7
Вок
1 1 1 1 1 0 0 0
1 1 1 1 0 1 0 0
-10
Сок
+ 1
1 1 1 1 0 1 0 1
Единицу переноса из знакового разряда компьютер
прибавляет к младшему разряду суммы для
корректировки результата.

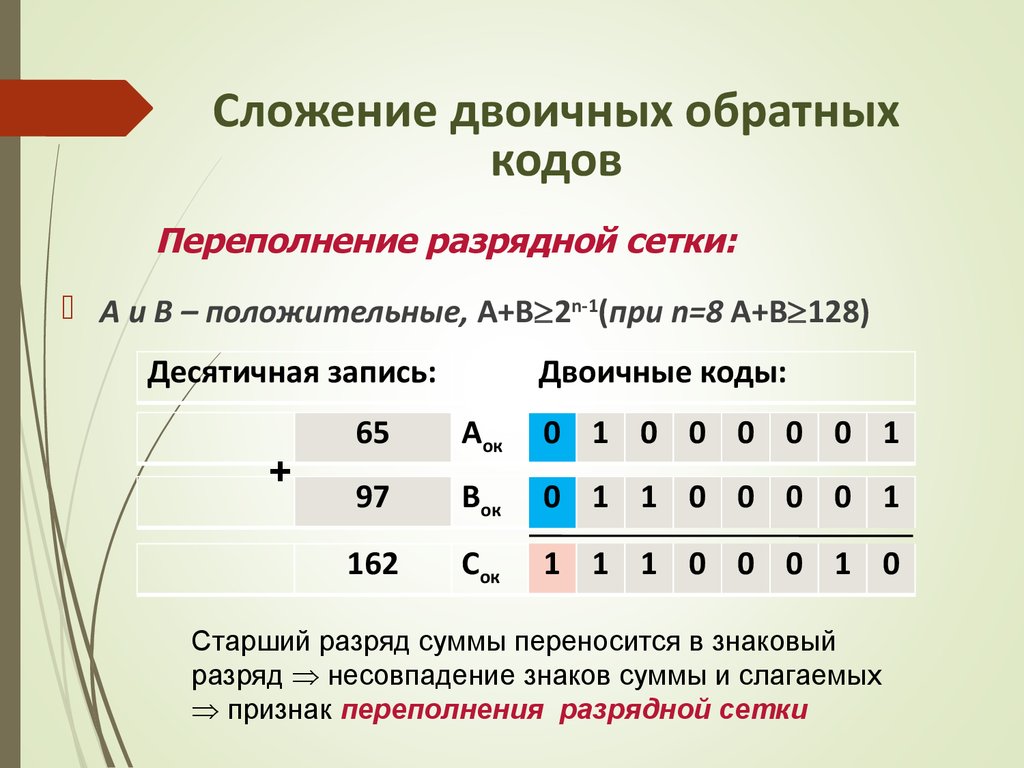
30. Сложение двоичных обратных кодов

Переполнение разрядной сетки:
А и В – положительные, A+B 2n-1(при n=8 A+B 128)
Десятичная запись:
+
Двоичные коды:
65
Аок
0 1 0 0 0 0 0 1
97
Вок
0 1 1 0 0 0 0 1
162
Сок
1 1 1 0 0 0 1 0
Старший разряд суммы переносится в знаковый
разряд несовпадение знаков суммы и слагаемых
признак переполнения разрядной сетки

31. Сложение двоичных обратных кодов

Переполнение разрядной сетки:
А и В – отрицательныетельные, A+B 2n-1
Десятичная запись:
Двоичные коды:
+
-63
Аок
1 1 0 0 0 0 0 0
-95
Вок
1 0 1 0 0 0 0 0
-158
Сок
0 1 1 0 0 0 0 0
+ 1
Несовпадение знаков суммы и слагаемых признак
переполнения разрядной сетки

32. Арифметические действия с дополнительными кодами

1) А – положительное, В – отрицательное,|B|>|A|
Десятичная запись:
+
Двоичные коды:
5
Апк
0 0 0 0 0 1 0 1
-12
Вдк
1 1 1 1 0 1 0 0
-7
Сдк
1 1 1 1 1 0 0 1
При переводе результата в прямой код биты цифровой части
результата инвертируются и к младшему разряду прибавляется
единица: 10000110 + 1 = 10000111= -710

33. Арифметические действия с дополнительными кодами

2) А – положительное, В – отрицательное, |B|<|A|
Десятичная запись:
+
Двоичные коды:
12
Апк
0 0 0 0 1 1 0 0
-5
Вдк
1 1 1 1 1 0 1 1
7
Спк
0 0 0 0 0 1 1 1
Перенос отбрасывается
Единицу переноса из знакового разряда компьютер отбрасывает.
В дополнительном коде сложение проще, чем в обратном

34. Арифметические действия с дополнительными кодами

3) А и В отрицательные
Десятичная запись:
+
Двоичные коды:
-5
Адк
1 1 1 1 1 0 1 1
-7
Вдк
1 1 1 1 1 0 0 1
-12
Сдк
1 1 1 1 0 1 0 0
Перенос отбрасывается
При переводе результата в прямой код биты цифровой части
результата инвертируются и к младшему разряду прибавляется
единица: 10001011+1= 10001100= -1210

35.

Сложение двоичных
дополнительных кодов
Переполнение разрядной сетки:
4. А>0, B>0, A+B 2n-1(при n=8 A+B 128)
5. А<0, B<0, A+B 2n-1
Ситуации рассматриваются по аналогии с
обратными кодами

36.

Сложение двоичных кодов с
фиксированной точкой
Сравнение обратной и дополнительной
форм кодирования отрицательных
чисел:
на преобразование отрицательных чисел в
обратный код требуется меньше времени, чем на
преобразование в дополнительный код;
время выполнения сложения для
дополнительных кодов чисел меньше, чем для их
обратных кодов.

37.

Умножение двоичных кодов с
фиксированной точкой
Умножение производится как последовательность
сложений и сдвигов в специальном регистре АЛУ накапливающем сумматоре
Пример. 1100112*1012
Накапливающий сумматор
000000000000
+
110011
+
110011
110011__
11111111
Регистр множителя
101
100
сдвиг на 2 позиции влево

38.

ПРЕДСТАВЛЕНИЕ С ФИКСИРОВАННОЙ
ТОЧКОЙ
Существенная ограниченность диапазона
представления чисел; (-)
Простота выполнения арифметических
действий; (+)
Отсутствие потери младших разрядов. (+)

39. ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ ТОЧКОЙ

Вещественные числа (конечные и бесконечные
десятичные дроби) хранятся и обрабатываются в
компьютере в формате с плавающей запятой.
В этом случае положение запятой в записи числа
может изменяться.
Формат чисел с плавающей запятой
базируется на экспоненциальной форме
записи, в которой может быть представлено
любое число.

40. ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ ТОЧКОЙ

Любое число N в системе счисления с основанием
можно представить в виде
N=M*q p ,
где M - мантисса числа, 1/q ≤|M|< 1
q - основание системы счисления,
p - порядок числа.
q

41. ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ ТОЧКОЙ

Нормализованная запись отличного от нуля
действительного числа – это запись вида
N=±M*q
p
Где p – целое число (положительное, отрицательное
или ноль);
M – правильная q -ичная дробь, у которой
первая цифра после запятой не равна нулю, то есть
1/q <= M < 1 .

42. ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ ТОЧКОЙ

Примеры нормализованной записи десятичных чисел:
3,14 = 0,314 * 101
2000 = 0,2 * 104
0,05 = 0,5 * 10-1
Примеры нормализованной записи двоичных чисел:
1 = 0,1 * 21
100 = 0,1 * 23
11,11010010 = 0,1111010010 * 22
0,01 = 0,1 * 2-1

43. Примеры нормализованного представления чисел с плавающей точкой

Десятичная система счисления:
3,14 = 0,314 * 101
2000 = 0,2 * 104
0,05 = 0,5 * 10-1
753,13=0,73513*103
-0,000034=-0,34*10-4
Двоичная система счисления:
1 = 0,1 * 21
11,11010010 = 0,1111010010 * 22
0,01 = 0,1 * 2-1
-101,01=-0,10101*23
-0,000011=-0,11*2-4

44. Определение максимального числа обычной точности

Число обычной точности занимает в памяти компьютера 4
байта.
Для хранения порядка мантиссы отводится 8 разрядов,
а для хранения мантиссы и её знака – 24 разряда.
01
1 1 11 1 1
01
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
знак и порядок
знак
и
мантисса
Максимальное значение порядка числа составит
11111112 =12710
Максимальное число
2127 = 1,7014118346046923173168730371588 × 1038

45. Максимальное значение мантиссы

Определение максимального числа
обычной точности
Максимальное значение мантиссы
223 - 1≈ 223 = 2(10×2,3) ≈ 10002,3 = 10 (3×2,3) ≈ 107
Точность вычислений определяется количеством
разрядов, отведённых для хранения мантиссы чисел.
Таким образом, максимальное значение чисел обычной точности
составит 1,701411 × 1038 (количество значащих цифр десятичного
числа в данном случае ограниченно 7 разрядами)

46. Сложение и вычитание чисел в формате с плавающей запятой

Сначала проводится подготовительная операция
выравнивание порядков.
Меньший по модулю порядок увеличивается до
величины большего по модулю порядка числа. Для того
чтобы величина числа не изменилась, мантисса
уменьшается в такое же количество раз (сдвигается в
ячейке памяти вправо на количество разрядов, равное
разрядности порядков чисел).
После выполнения операции выравнивания одинаковые
разряды чисел оказываются расположенными в одних и
тех же разрядах ячеек памяти. Теперь операции
сложения и вычитания чисел сводятся к сложению или
вычитанию мантисс.

47. Сложение и вычитание чисел в формате с плавающей запятой

0,1 × 25 + 0,1 × 23 = ?
0,1 × 25 - 0,1 × 23 = ?
0,100 × 25
0,100 × 25
+
0,001 × 25
0,001 × 25
______________
_________________
0,101 × 25
0,010 × 25 = 0,10 × 24

48. Умножение и деление чисел с плавающей запятой

При умножении чисел в формате с плавающей
запятой порядки складываются, а мантиссы
перемножаются.
При делении из порядка делимого вычитается
порядок делителя, а мантисса делимого
делится на мантиссу делителя.
Затем число обязательно нормализуется, т. е.
после запятой должна стоять цифра, отличная от
нуля.

49. Умножение и деление чисел с плавающей запятой

Умножение
0,1 × 25
×0,1 × 23
_________________
0,01 × 28 = 0,1 × 27
Деление
0,1 × 25
: 0,1 × 23
______________
1 × 22 = 0,1 × 23

50.

ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ
ТОЧКОЙ
Число двойной точности занимает в памяти компьютера
8 байт.
Чем больше разрядов отводится под запись
мантиссы, тем больше точность представления
числа.
Чем больше разрядов занимает порядок, тем
больше диапазон представления чисел.

51.

ПРЕДСТАВЛЕНИЕ С ПЛАВАЮЩЕЙ
ТОЧКОЙ
СРАВНЕНИЕ С ПРЕДСТАВЛЕНЕМ
С ФИКСИРОВАННОЙ ТОЧКОЙ:
¨ Большой диапазон представления чисел. (+)
¨ Уменьшается количество значащих цифр, так
как часть бит отводится под порядок. (-)
¨ Возможна потеря точности при выполнении
операций за счет отбрасывания младших
разрядов. (-)
¨ Усложнение выполнения арифметических
операций.(-)

52. ЗАДАНИЕ ДЛЯ ПОДГОТОВКИ К КОНТРОЛЬНОЙ РАБОТЕ

1. Перевести из десятичной системы в
шестнадцатеричную, восьмеричную, двоичную, а
затем проверить правильность перевода:
155, 34.5, 206.125, 999.01
2. В какой системе счисления справедливо:
21+24=100; 22+34=100?
3. Записать в прямом, обратном и дополнительном
двоичном коде в однобайтовом формате следующие
десятичные числа: -12, 88, -125.

53.

ЗАДАНИЕ ДЛЯ ПОДГОТОВКИ
К КОНТРОЛЬНОЙ РАБОТЕ
4. Представить в нормализованном виде в
двоичной системе счисления следующие
десятичные числа:
25.115, -15.64, 0.0056, -0.5.
5. Числа п.3 записать в форме с плавающей
точкой в 32-разрядную ячейку памяти.