Элементы релятивистской механики. Специальная теория относительности. (Лекция 4.2)

1.

ЛЕКЦИЯ 4,
4 часть 2.
Кафедра физики
Элементы релятивистской механики
План лекции
ных
з
а
р
в
а тел
н
и
л
Д
нца.
е
р
о
Л
я
овани
з
а
р
б
ни
о
е
е
м
р
е
р
в
к
1. П
а
о
жут
счет
е
т
о
м
о
х
р
а
П
м
е
.
т
сис
енца
р
о
Л
я
и
н
азова
р
б
о
е
и
р
е
П
и
н
.
а
2.
в
и
о
м
з
я
а
еобр
быти
р
о
с
П
у
.
д
а
ж
ц
е
н
м
ор е
Л
я
и
н
а
в
о
раз
с а.
й.
ь
е
3. Преоб
л
т
у
с
п
о
р
м
о
и
к
с
я
сложение кое выражение дл
и.
и
г
р
е
н
э
с
т
я
дл
вис
4. Реляти стское выражение
ви
и
т
я
л
е
Р
5.
Общая физика. Раздел «Элементы релятивистской механики"
1

2.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
1. Одновременность событий
в разных системах отсчета.
y
y*
К
v0
К*
Пусть в системе отсчета К в точках
0
с координатами х1 и х2 происходят
0*
x
z*
одновременно два события в z
момент времени t 1 t 2 T.
T ( / c ) x1
T ( / c ) x2
*
*
*
t1
,
t2
Запишем для К :
1 2
1 2
x*
Видно, что если события в системе К пространственно разобщены,
т.е.* x 1 * x 2 , то в системе *К* они
не будут одновременными
*
t
t
1 ) . Знак разности t 2 t 1 определяется знаком выражения
( 2
( / c )( x1 x 2 )
Общая физика. Раздел «Элементы релятивистской механики"
2

3.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
2. Длина тел в разных
системах отсчета .
Рассмотрим расположенный
*
вдоль оси x
стержень,
*
покоящийся относительно K .
y
y*
К
0
z
z*
Стержень движется относительно
системы K
vсо v 0
K*
скоростью
. Определим
x1*
его длину.
Отметим в системе K координаты концов
стержня x*1 и x*2 в момент времени t 1 t 2 T
Общая физика. Раздел «Элементы релятивистской механики"
К*
v0
0*
x*
x
x*
l0
x*2
3

4.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
y
y*
2. Длина тел в разных
системах отсчета .
К
v0
l x 2 x1
- длина стержня,
измеренная
в
системе .K
0
0*
Воспользуемся преобразованиями z
x
z*
Лоренца.
x 2 v0 T
x1 v 0 T
*
*
x1
,
x2
*
2
2
2
2
K
1 v0 c
1 v0 c
x1*
x 2 x1
l0
x*2 х1*
1 v02 c 2
Лоренцево сокращение
К*
x*
x*
x*2
l l0 1 v 2 c 2
Общая физика. Раздел «Элементы релятивистской механики"
4

5.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
3. Промежуток времени
y
между событиями.
К
*
K
Пусть в системе
происходят два
события.
Первому событию
0
* a
x
соответствует координата
и
1
*
z
z*
момент времени t 1 .
y*
К*
v0
0*
*
x*
x
*
Второму событию * соответствует координата x1 x 2 a
t2 .
и момент времени
Воспользуемся преобразованиями Лоренца для перехода в систему
отсчета K .
t1
t 1* ( v0 / c 2 )a
1
v02
c
2
,
t2
t *2 ( v0 / c 2 )a
Общая физика. Раздел «Элементы релятивистской механики"
1 v02 c 2
5

6.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
y
3. Промежуток времени
между событиями.
t 2 t1
К
t *2 t1*
1 v 02
Введем обозначения:
y*
0
c
2
t 2 t 1 t ,
z
z*
К*
v0
0*
x*
x
t *2 t1* t *
Пусть события происходят с одной и той *же
частицей, которая покоится в системе K и
Δt
v v 0,
движется со скоростью
если
1 v 02 c 2
наблюдение вести из системы K .
*
Тогда t собственное
время
2 c2
*
Δτ
Δt
1
v
0
частицы (в системе K )
Δt *
Движущиеся часы идут медленнее, чем неподвижные.
Общая физика. Раздел «Элементы релятивистской механики"
6

7.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
4. Преобразование скоростей
Компоненты скорости v частицы в
системе K равны
dy
dz
dx
, vz
vx
, vy
dt
dt
dt
*
В *системе K компоненты скорости
v той же частицы равны
v*x*
dz *
dx* *
dy*
*
* , v y* * , v z* *
dt
dt
dt
Найдем формулы, связывающие компоненты скорости в разных
системах. Запишем преобразования Лоренца
x
x* v 0 t *
1 v02 c 2
,
y y* ,
z z* , t
Общая физика. Раздел «Элементы релятивистской механики"
t * (v0 /c 2 ) x*
1 v02 c 2
7

8.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
4. Преобразование скоростей
Получим следующие выражения:
Разделив первую формулу
на четвертую, получим
dx
dx* v 0 dt *
1 v02 c 2
dy dy* ,
dt
dz dz*
dt * (v0 /c 2 ) dx*
1 v 02 c 2
dx* v0 dt *
dx* dt * v0
dx
*
2
*
dt dt ( v0 c ) dx
1 ( v0 c 2 ) dx* dt *
Общая физика. Раздел «Элементы релятивистской механики"
8

9.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
4. Преобразование скоростей
dx
dx*
dx
Поскольку
v x , а * v*x* , то
dt
dt
vx
dx * v 0 dt *
1 v 02 c 2
dy dy* ,
v* v0
dt
*
dz dz *
dt * ( v 0 / c 2 )dx *
1 v 02 c 2
x
1 v* v0 c 2
x*
Аналогичным образом получим выражения
для v y и v z , разделив формулы 2 и 3 на
формулу 4:
vy
v*
*
y
1 v02 c 2
*
1 v v0 c
x*
2
vz
v *z
*
1 v 02 c 2
1 v* v0 c 2
Общая физика. Раздел «Элементы релятивистской механики"
x*
9

10.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Преобразования Лоренца. Некоторые следствия.
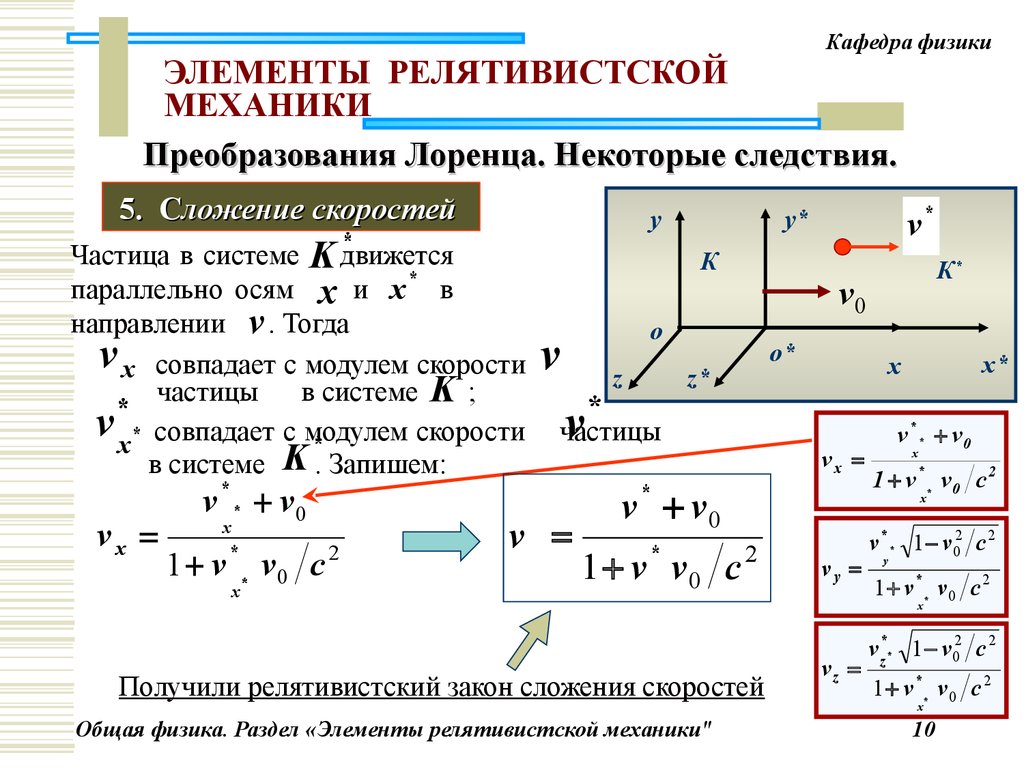
5. Cложение скоростей
y
*
Частица в системе K движется
параллельно осям x и x* в
направлении v . Тогда
v x совпадает с модулем скорости
частицы
в системе K ;
*
v x* совпадает с модулем
скорости
*
в системе K . Запишем:
vx
v* * v0
x
1 v** v0 c 2
x
К
v
о
z
*
v
частицы
v
v*
y*
z*
v0
о*
Получили релятивистский закон сложения скоростей
Общая физика. Раздел «Элементы релятивистской механики"
x*
x
vx
v* v0
1 v* v0 c 2
К*
v* * v0
x
1 v** v0 c 2
x
vy
v * * 1 v 02 c 2
y
1 v** v 0 c 2
x
vz
v *z* 1 v 02 c 2
1 v** v 0 c 2
x
10

11.

ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Кафедра физики
Релятивистское выражение для импульса
p m v - выражение для импульса тела в классической механике;
p
p
mv
2
1 v c
2
1
1 v2 c2
- выражение для релятивистского импульса тела.
mv
d
mv
F
dt 1 v 2 c 2
- удобная для запоминания форма записи.
- второй закон Ньютона в
релятивистской механике .
Общая физика. Раздел «Элементы релятивистской механики"
11

12.

ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Кафедра физики
Релятивистское выражение для энергии
Выражение для энергии получим, используя второй закон Ньютона.
Умножим выражение на перемещение частицы ds vdt.
Левая часть -выражение для работы.
d
mv
vdt
Fds
Правая часть - приращение кинетической
dt 1 v 2 c 2 .
энергии частицы T за время dt .
.
d
mv
mv
vdt vd
dT
2
2
dt 1 v 2 c 2
1 v c
vdv d v 2 2
Общая физика. Раздел «Элементы релятивистской механики"
12

13.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Релятивистское выражение для энергии
mdv
mv v dv c 2
md v 2 2
mc 2 d v 2 c 2
dT v
3
3
3
2
2
2
2 2
2
2 2
2
2 2
1
v
c
1 v c
1 v c
2 1 v c
2
mc
После интегрирования
dT d
T
2
2 получим:
1 v c
mc 2
2
1 v c
2
const
Определим выражение для константы. При v 0 кинетическая
энергия обращается в нуль. Следовательно const mc 2
Итог:
T
mc mc
1
2
2
2
2
1 v c
1 v c
mc 2
2
2
1
Общая физика. Раздел «Элементы релятивистской механики"
13

14.

Кафедра физики
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
МЕХАНИКИ
Релятивистское выражение для энергии
В релятивистской механике свободная частица кроме кинетической
энергии обладает еще так называемой энергией покоя E0
E 0 mc
Выражение для полной энергии
2
E частицы выглядит так:
E T E 0 T mc 2
Подставим в это выражение формулу
для кинетической энергии, получим
окончательно
E
Общая физика. Раздел «Элементы релятивистской механики"
mc 2
1 v2 c2
14