Функции издержек

1. Поиск оптимального плана – точки равновесия х*

• выпуск заданного
количества
продукции q с
наименьшими
переменными
издержками
G ( x) w x min,
при условии
q ( x) const
x 0.
• выпуск
максимального
количества
продукции при
наличии бюджетного
ограничения
q ( x) max
при условии
G ( x) w x const
x 0.

2. Точка равновесия x*

• касательная
• угловая
• x* - точка касания
изокосты с
изоквантой, причем
задействованы все
ресурсы
• точка равновесия
лежит на одной из
осей
x1* > 0, x2* > 0
одна из
координат точки
равна 0

3. Изокоста

- множество планов производства с
одинаковыми переменными издержками
• Уравнение изокосты
G ( x) w1 x1 w2 x2 c
• Семейство изокост на плоскости –
множество отрезков параллельных прямых
w ( w1 , w2 )
с нормалью
• Угол наклона изокосты к оси Оx1
определяется отношением цен на ресурсы:
tg = – w1/ w2.

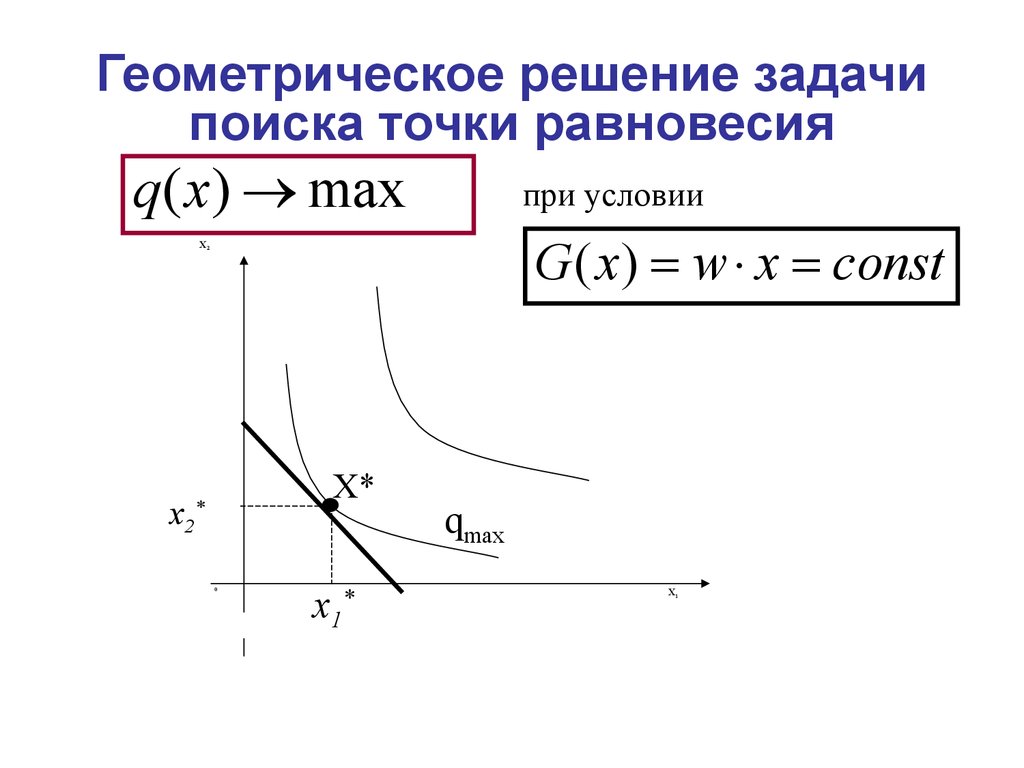
4. Геометрическое решение задачи поиска точки равновесия

q ( x) max
при условии
G ( x) w x const
X2
x
X*
*
2
0
x1
*
qmax
X1

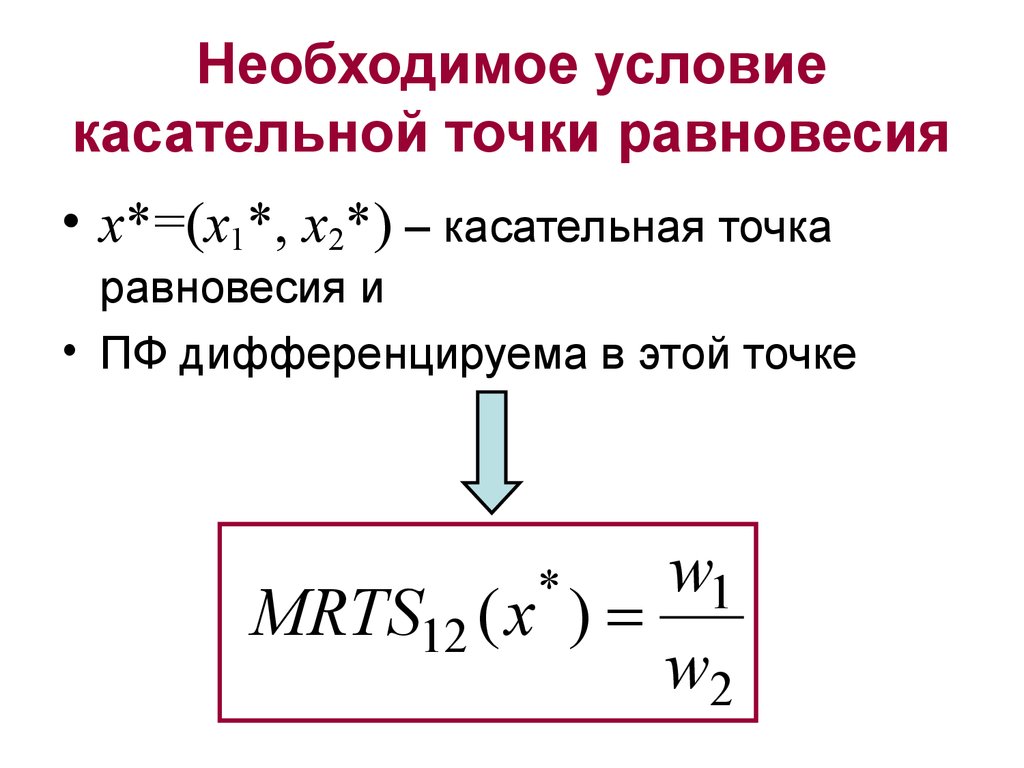
5. Необходимое условие касательной точки равновесия

• x*=(x1*, x2*) – касательная точка
равновесия и
• ПФ дифференцируема в этой точке
w1
MRTS12 ( x )
w2
*

6. Правило равной производительности ресурсов на единицу затрат

MP1 w1
MP1 MP2
MRTS12
MP2 w2
w1
w2
• Производитель заменяет один ресурс другим, пока это
выгодно.
• Отдачи ресурсов в расчете на единицу затрат
равны для всех используемых ресурсов.
• Рубль затрат в любой ресурс приносит одинаковый
эффект.
• В рыночной экономике происходит согласование
способа производства с соотношением цен на факторы,
• производительность факторов (отдача ресурсов)
должна соответствовать их стоимости,
• в результате ограниченные ресурсы используются
самым эффективным способом.

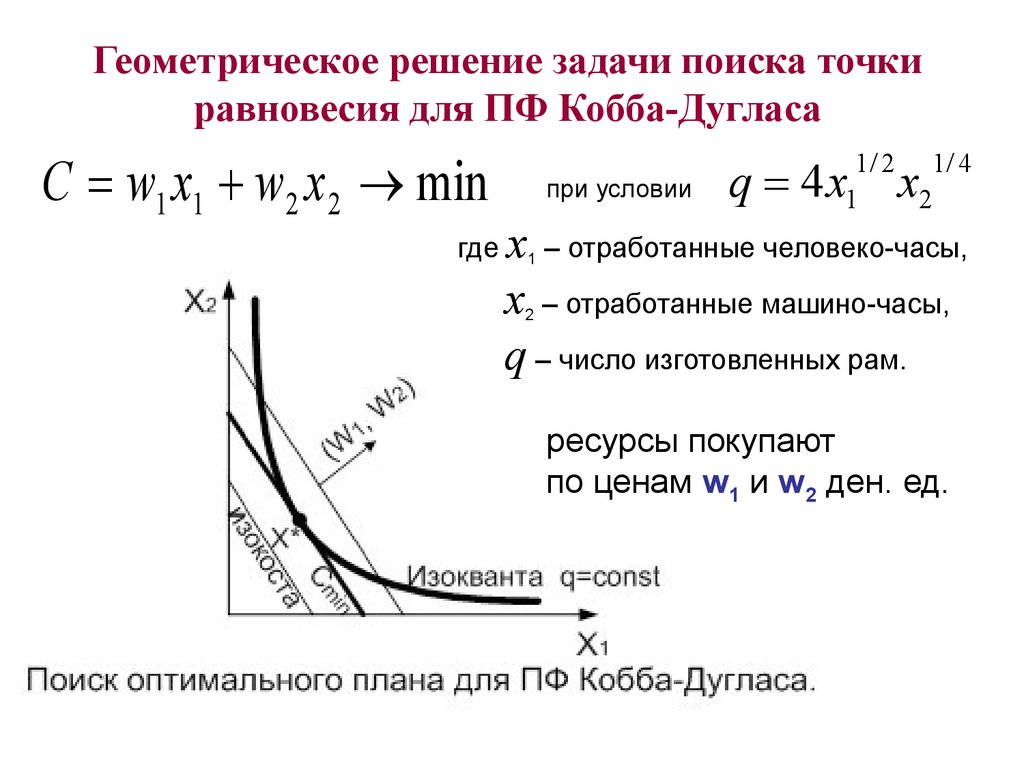
7.

Геометрическое решение задачи поиска точки
равновесия для ПФ Кобба-Дугласа
C w1 x1 w2 x 2 min
где
при условии
1/ 2 1/ 4
1
2
q 4x
x
x – отработанные человеко-часы,
x – отработанные машино-часы,
q – число изготовленных рам.
1
2
ресурсы покупают
по ценам w1 и w2 ден. ед.

8. Геометрическое решение задачи поиска точки равновесия

Поиск оптимального плана для линейной ПФ
G ( x) w1 x1 w2 x2 min
a1 x1 a2 x2 q,
• в одной системе координат построим
изокванту и семейство изокост
• Для определенности предположим, что
w1/w2 > a1/a2
• план х* – самый дешевый, обеспечивающий
выпуск q единиц продукции.
• Получили угловую точку равновесия
argmin G(x) = x* = (0, q/a2).

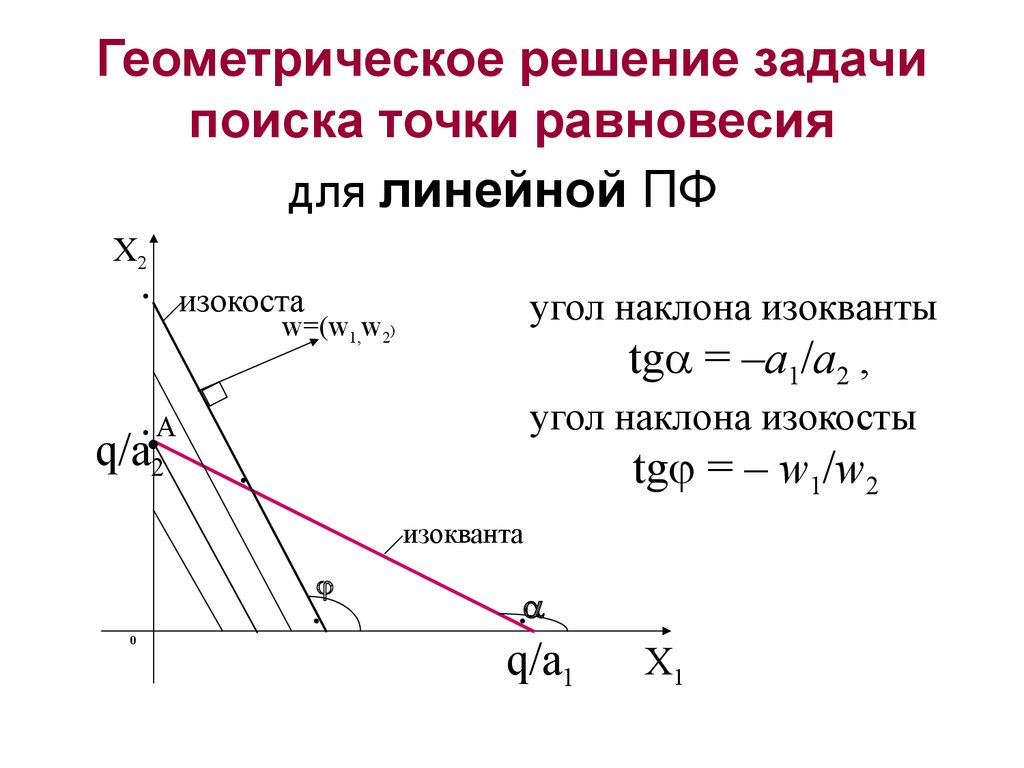
9. Геометрическое решение задачи поиска точки равновесия

для линейной ПФ
X2
изокоста
угол наклона изокванты
tg = –a1/a2 ,
угол наклона изокосты
w=(w1,w2)
A
q/a2
tg = – w1/w2
изокванта
0
q/a1
X1

10. Необходимое условие угловой точки равновесия

• Если оптимальный план x*=(0, x2*)
(невыгодно использовать даже первую
единицу первого ресурса), то
w1
MRTS12 ( x )
w2
*
• Если оптимальный план x*=(x1*,
w1
MRTS12 ( x )
w2
*
0), то

11. Функции издержек

12. Построение функции переменных издержек

G ( x) w x min,
Пусть задача минимизации издержек имеет единственное решение:
x*=(x1*, x2*, ..., xn*) - план производства по ресурсам, обеспечивающий
выпуск q единиц продукции = оптимальный план по ресурсам =
точка равновесия производителя.
функция спроса на ресурсы:
стоимость этих ресурсов
*
*
x x ( w, q)
w x * ( w, q )
• функция переменных издержек
денежных единиц.
*
C v ( w, q ) w x ( w, q )
сопоставляет объему выпуска q и ценам ресурсов w
стоимость плана, обеспечивающего выпуск q единиц продукции с
наименьшими переменными издержками,
• функция общих издержек
C (q ) C0 Cv (q).

13. Функция переменных издержек для линейной ПФ

w1/w2 > a1/a2
X2
Угловая точка равновесия:
изокоста
argmin G(x) = x* = (0, q/a2).
w=(w1,w2)
Стоимость ресурсов в
оптимальном плане
A
q/a2
Gmin=Сv(q)=w2 q/a2
изокванта
0
ден.ед.
q/a1
X1
В общем случае, для линейной ПФ
функция переменных издержек Сv(q)=min{w1/a1, w2/a2}q.

14.

Геометрическое решение задачи поиска точки
равновесия для ПФ Кобба-Дугласа
C w1 x1 w2 x 2 min
где
при условии
1/ 2 1/ 4
1
2
q 4x
x
x – отработанные человеко-часы,
x – отработанные машино-часы,
q – число изготовленных рам.
1
2
ресурсы покупают
по ценам w1 и w2 ден. ед.

15. Однородные функции

• Функция нескольких переменных называется
однородной порядка m, если для всех х из
некоторой области Х
f (kx1 , kx 2 ,..., kx n ) k f ( x1 , x 2 ,..., x n )
m
• Если ПФ является однородной
порядка m, то
• при m=1 ПФ обладает постоянным;
• при m>1 ПФ обладает возрастающим
• при m<1 ПФ обладает убывающим
эффектом
масштаба

16. Функция издержек однородной ПФ

Теорема. Если ПФ является однородной
порядка (степени) m, то
• функция спроса на ресурсы
1 1/ m
x(q) x q
1
где x – план по ресурсам, обеспечивающий
выпуск единицы продукции с наименьшими
переменными издержками
(стоимость плана x1 есть Cv(1)=С1),
• функция переменных издержек
C v (q) C v (1)q
1/ m
.

17.

• Следствие. Если ПФ характеризуется
постоянным эффектом масштаба
(является однородной степени 1), то
она порождает линейную функцию
издержек
C ( q ) C0 C 1 q

18. Влияние эффекта масштаба на вид кривой издержек

постоянный
X2
C
3x2
3q
2x2
2C
2q
C
x2
0
q
x1
2x1
3x1
X1
q
2q
q

19. Влияние эффекта масштаба на вид кривой издержек

убывающий
X2
C
2q
2x2
x2
2C
C
q
0
x1
2x1
X1
q
2q
q

20. Влияние эффекта масштаба на вид кривой издержек

возрастающий
C
X2
2C
C
2x2
2q
x2
0
q
x1
2x1
X1
q
2q
q

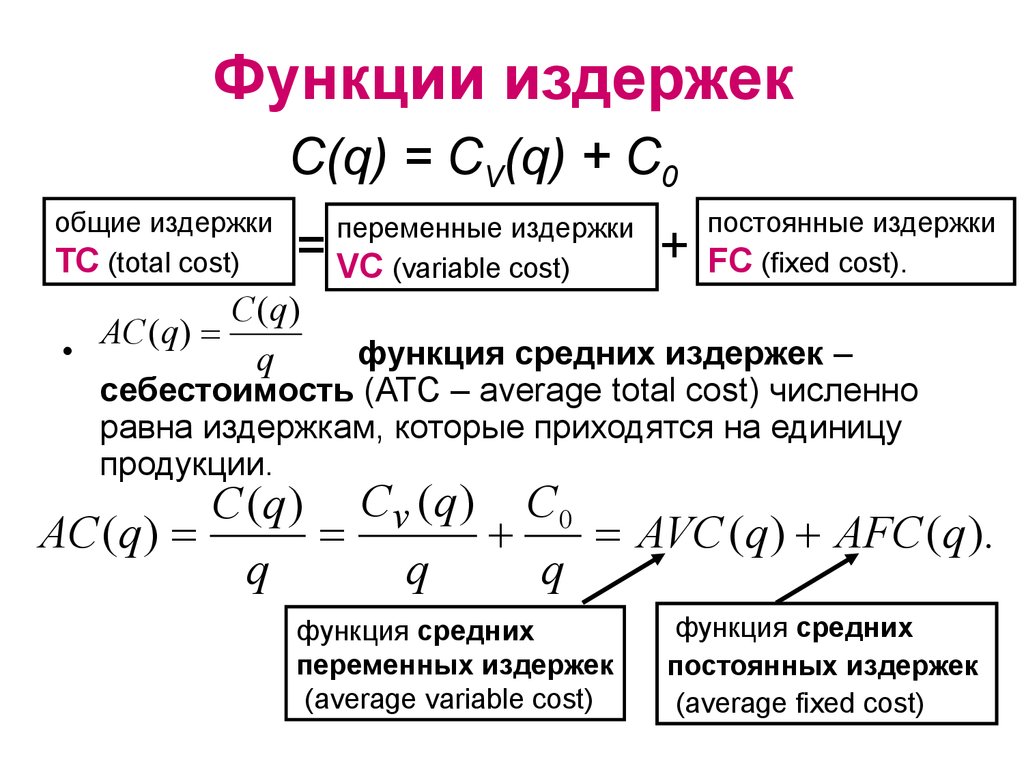
21. Функции издержек

С(q) = CV(q) + С0
общие издержки
TC (total cost)
=
переменные издержки
VC (variable cost)
+
постоянные издержки
FC (fixed cost).
C (q)
AC (q )
функция средних издержек –
q
себестоимость (ATC – average total cost) численно
равна издержкам, которые приходятся на единицу
продукции.
C (q) Cv (q) C 0
AC (q )
AVC (q ) AFC (q ).
q
q
q
функция средних
переменных издержек
(average variable cost)
функция средних
постоянных издержек
(average fixed cost)

22. Предельные издержки

Предельные издержки
C (q ) - функция предельных издержек.
Cv (q ) C (q )
= MC(q) (marginal cost).
• Экономическая интерпретация
предельных издержек: величина
предельных издержек при данном объеме
выпуска показывает, на сколько денежных
единиц приблизительно возрастут издержки,
если увеличить объем выпуска на единицу
C (q ) C (q 1) C (q )
q 1 MC (q ) C

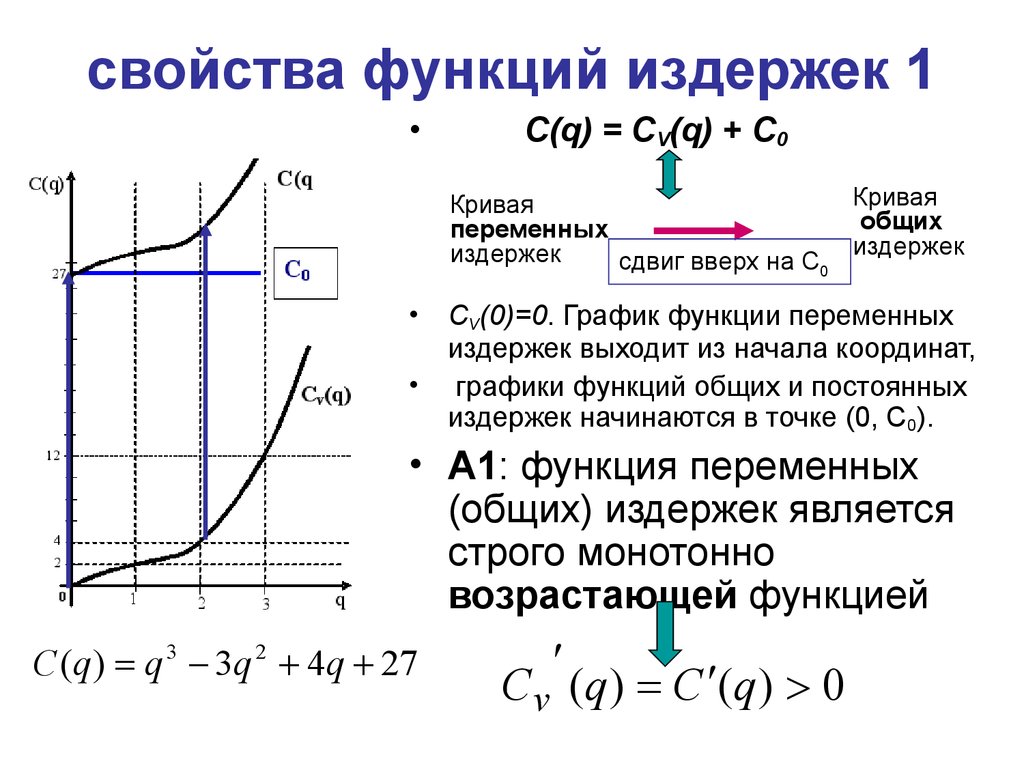
23. свойства функций издержек 1

С(q) = CV(q) + С0
Кривая
Кривая
общих
переменных
издержек
издержек
сдвиг вверх на С0
CV(0)=0. График функции переменных
издержек выходит из начала координат,
графики функций общих и постоянных
издержек начинаются в точке (0, С0).
• A1: функция переменных
(общих) издержек является
строго монотонно
возрастающей функцией
C (q) q 3 3q 2 4q 27
C v (q ) C (q ) 0

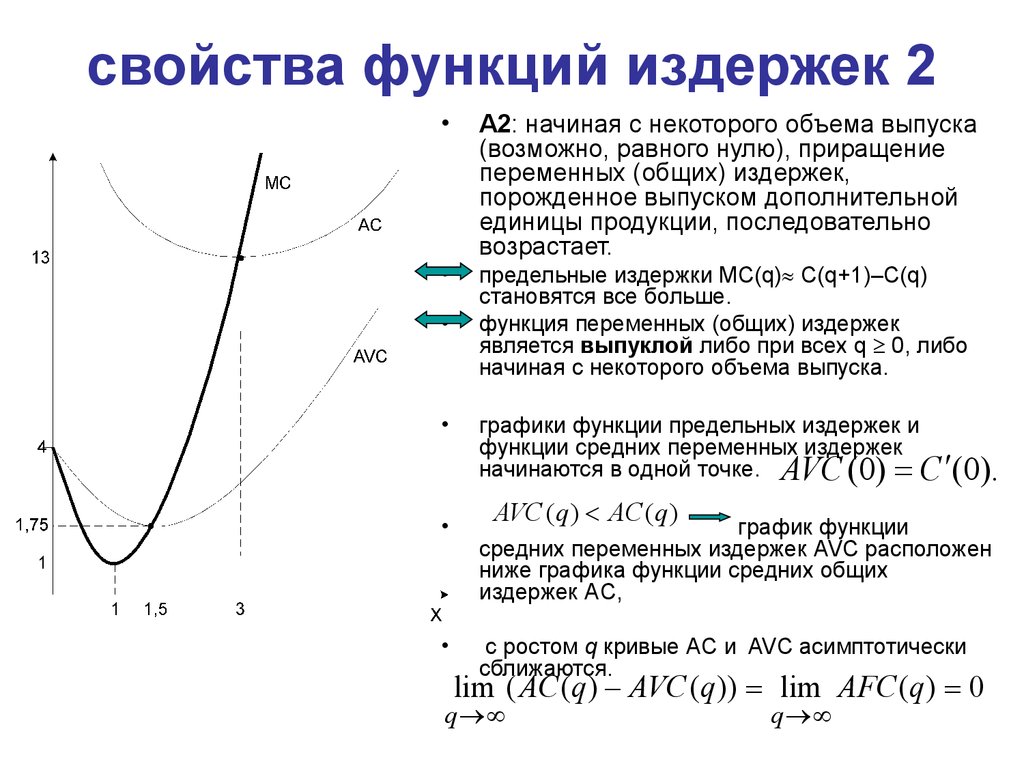
24. свойства функций издержек 2

A2: начиная с некоторого объема выпуска
(возможно, равного нулю), приращение
переменных (общих) издержек,
порожденное выпуском дополнительной
единицы продукции, последовательно
возрастает.
предельные издержки MC(q) C(q+1)–C(q)
становятся все больше.
функция переменных (общих) издержек
является выпуклой либо при всех q 0, либо
начиная с некоторого объема выпуска.
графики функции предельных издержек и
функции средних переменных издержек
начинаются в одной точке. AVC (0) C (0).
AVC (q ) AC (q )
график функции
средних переменных издержек AVC расположен
ниже графика функции средних общих
издержек AC,
с ростом q кривые AC и AVC асимптотически
сближаются.
lim ( AC (q ) AVC (q )) lim AFC (q ) 0
q
q

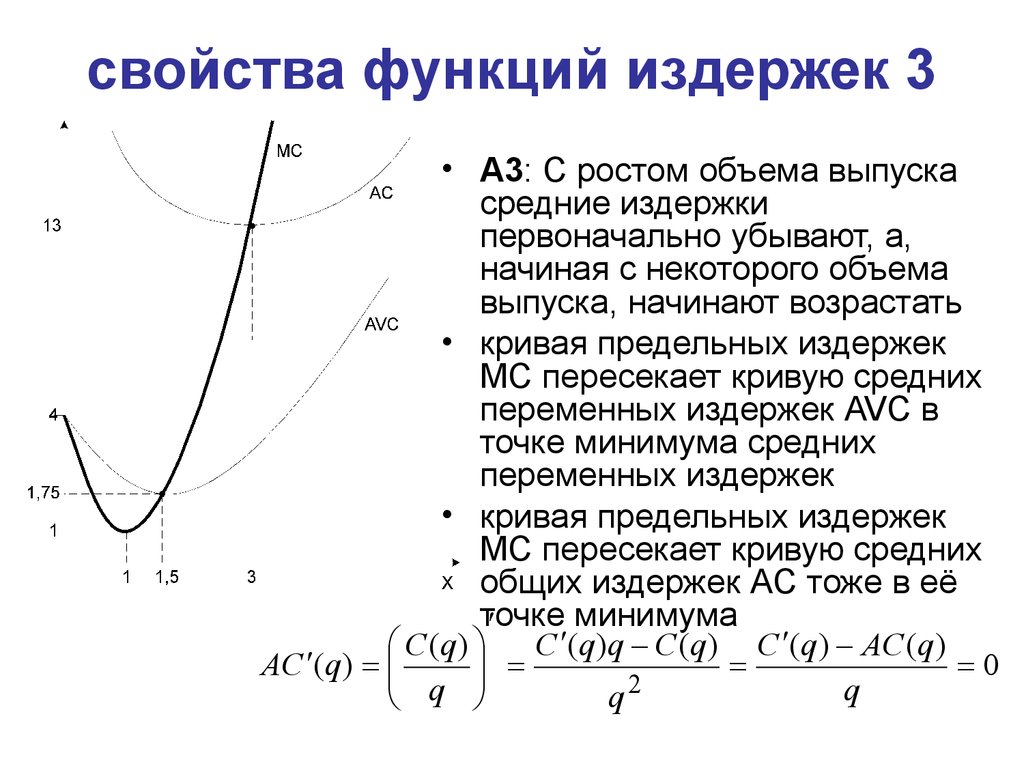
25. свойства функций издержек 3

• A3: C ростом объема выпуска
средние издержки
первоначально убывают, а,
начиная с некоторого объема
выпуска, начинают возрастать
• кривая предельных издержек
MC пересекает кривую средних
переменных издержек AVC в
точке минимума средних
переменных издержек
• кривая предельных издержек
MC пересекает кривую средних
общих издержек AC тоже в её
точке
минимума
C (q)
C (q) q C (q) C (q ) AC (q )
AC (q)
0
2
q
q
q

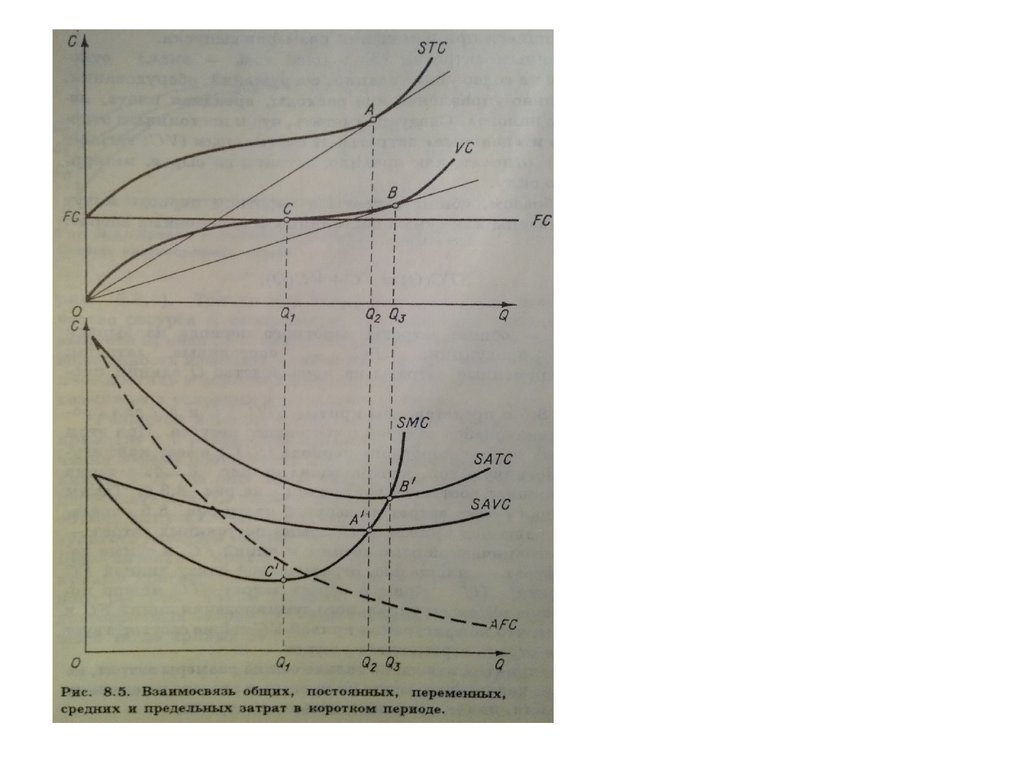
26. На кривой общих затрат ТС

• предельные затраты МС определяются
тангенсом угла наклона касательной
• средние затраты АС определяются тангенсом
угла наклона луча, проведенного из начала
координат к кривой
Средние затраты достигают минимума
при таком объёме выпуска, когда они
равны предельным затратам