Аксиоматический метод. Метод следов

1.

Аксиоматический метод
Метод следов
Суть метода заключается в построении
вспомогательной прямой, являющейся изображением
линии пересечения секущей плоскости с плоскостью
какой-либо грани фигуры . Удобнее всего строить
изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют
следом секущей плоскости. Используя след, легко
построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры .

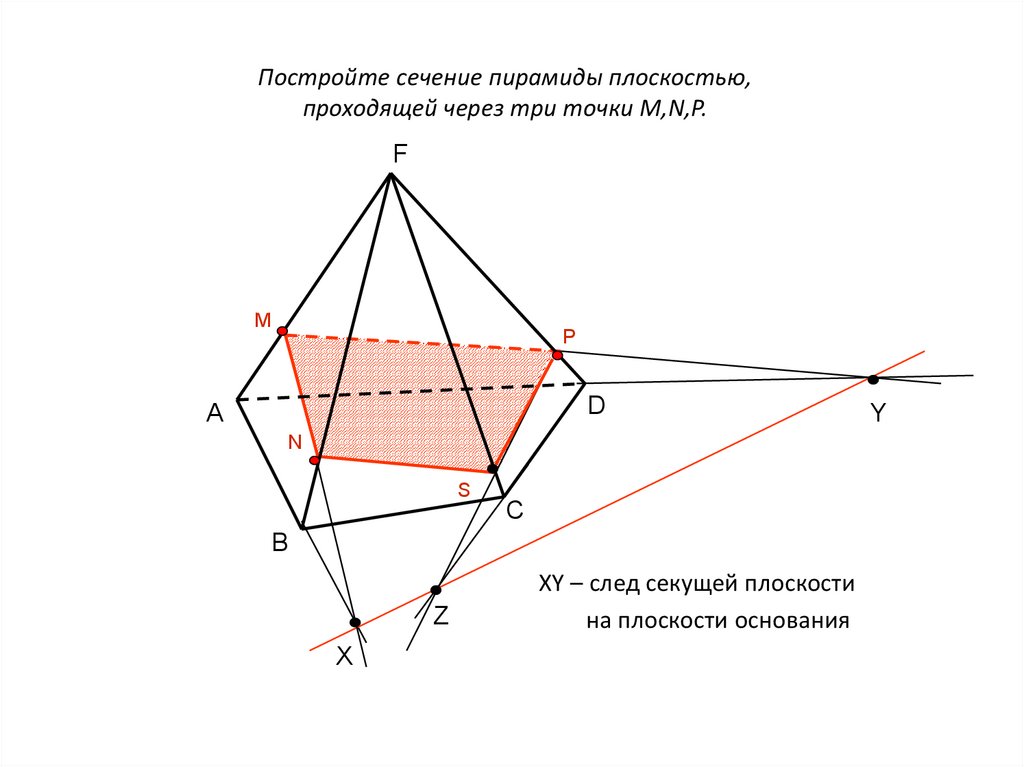
2. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
M
P
D
А
N
S
C
B
Z
X
XY – след секущей плоскости
на плоскости основания
Y

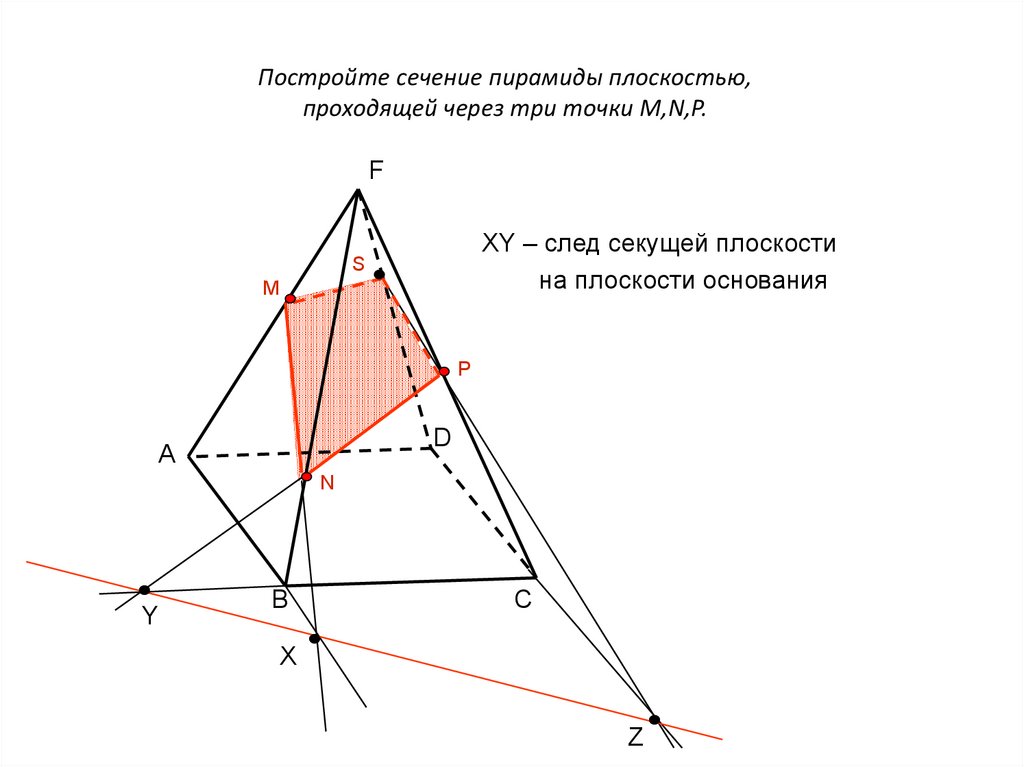
3. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
XY – след секущей плоскости
на плоскости основания
S
M
P
D
А
N
Y
B
C
X
Z

4.

Выбираем точки М и N, принадлежащие одной грани и строим прямую MN –
«след» пересечения правой грани и секущей плоскости.
K
D1
C1
A1
B1
N
D
A
M
C
B
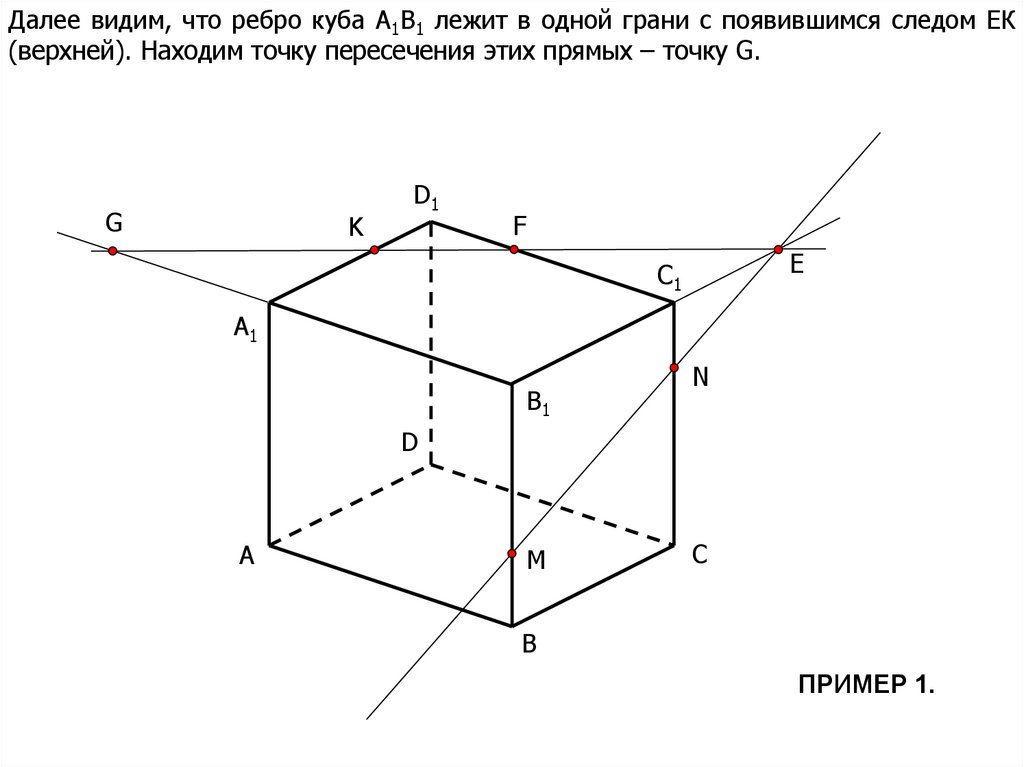
ПРИМЕР 1.

5.

Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани с
третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN
(правой). Находим точку пересечения этих прямых – точку Е.
K
D1
E
C1
A1
B1
N
D
A
M
C
B
ПРИМЕР 1.

6.

Точки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК –
«след» их пересечения и F D1C1, EK.
K
D1
F
E
C1
A1
B1
N
D
A
M
C
B
ПРИМЕР 1.

7.

Далее видим, что ребро куба А1В1 лежит в одной грани с появившимся следом ЕК
(верхней). Находим точку пересечения этих прямых – точку G.
G
K
D1
F
E
C1
A1
B1
N
D
A
M
C
B
ПРИМЕР 1.

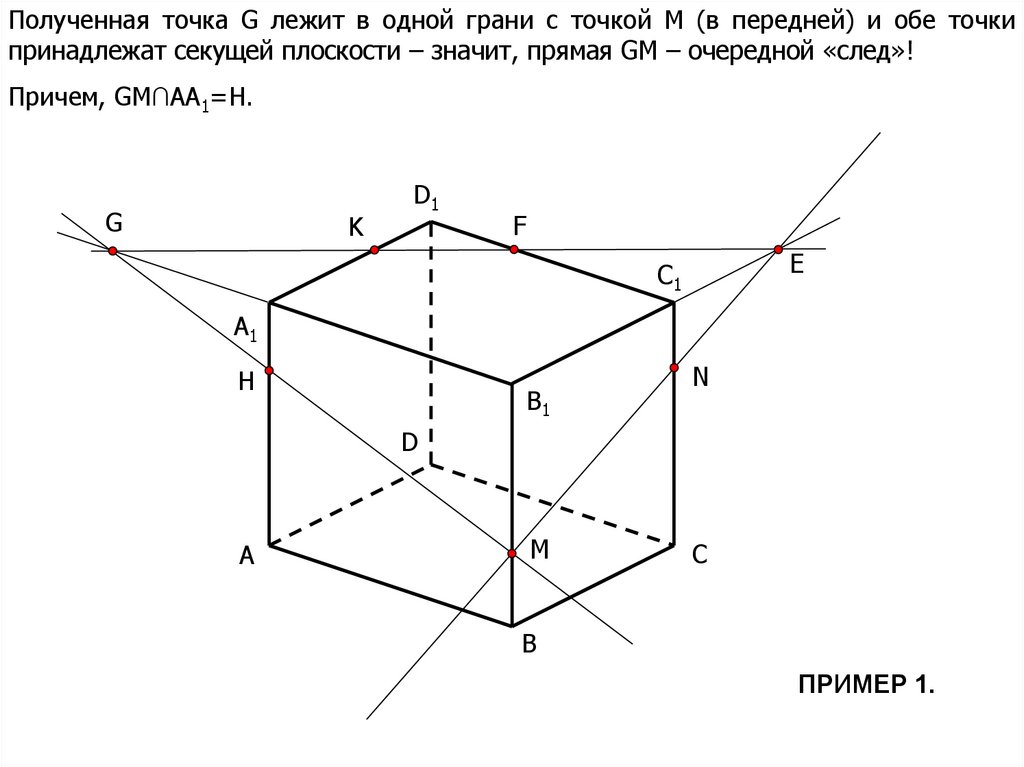
8.

Полученная точка G лежит в одной грани с точкой М (в передней) и обе точки
принадлежат секущей плоскости – значит, прямая GM – очередной «след»!
Причем, GM∩АА1=Н.
G
K
D1
F
E
C1
A1
H
B1
N
D
A
M
C
B
ПРИМЕР 1.

9.

Остается соединить отрезками все пары точек, лежащие в секущей
плоскости и в одной грани куба.
G
K
D1
F
E
C1
A1
H
B1
N
D
A
M
C
B
ПРИМЕР 1.
Полученный пятиугольник MNFKH – искомое сечение куба.

10.

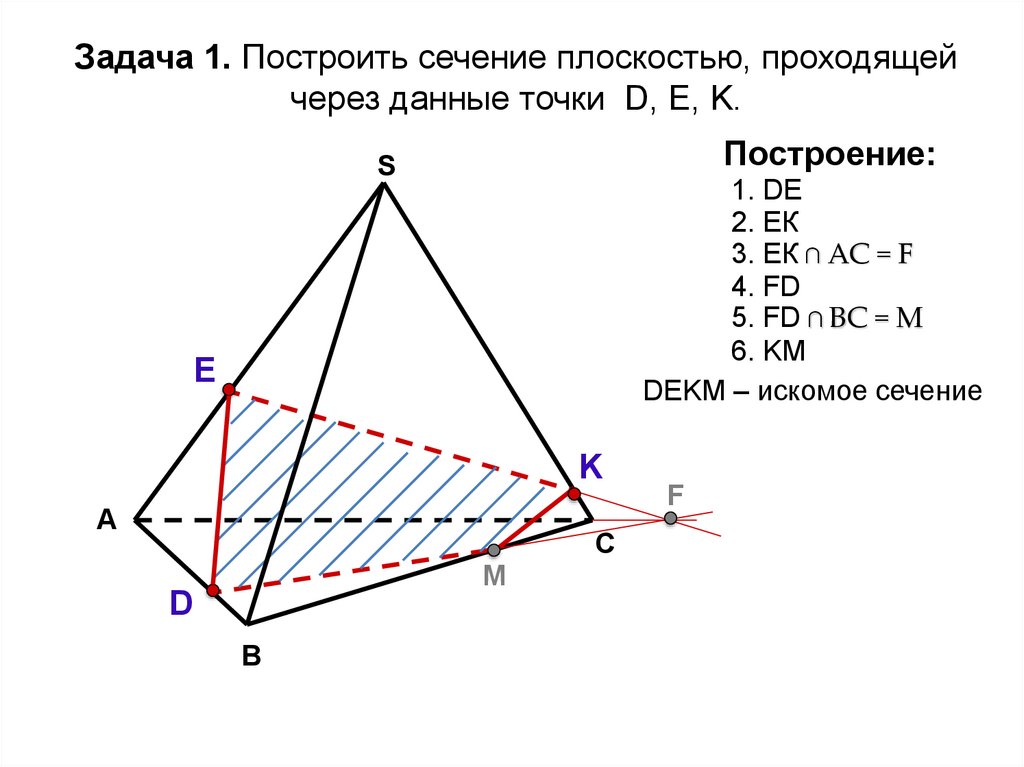
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

11.

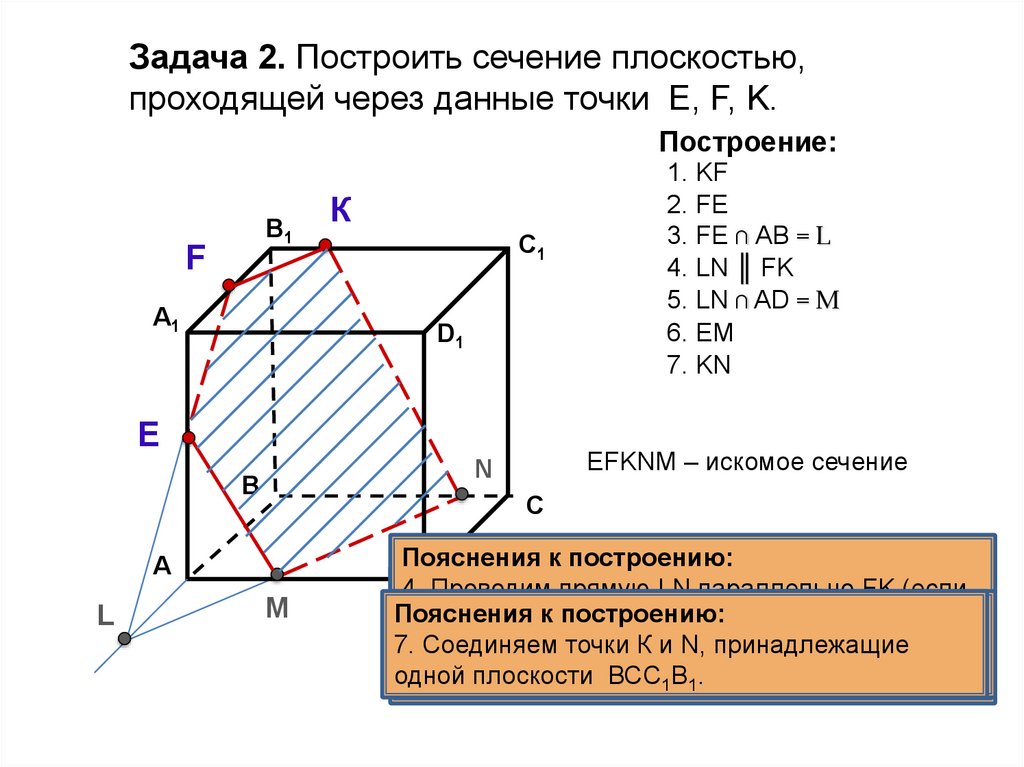
Задача 2. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
вАА
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
А1точке
В1В
1С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

12.

Задача 3. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

13.

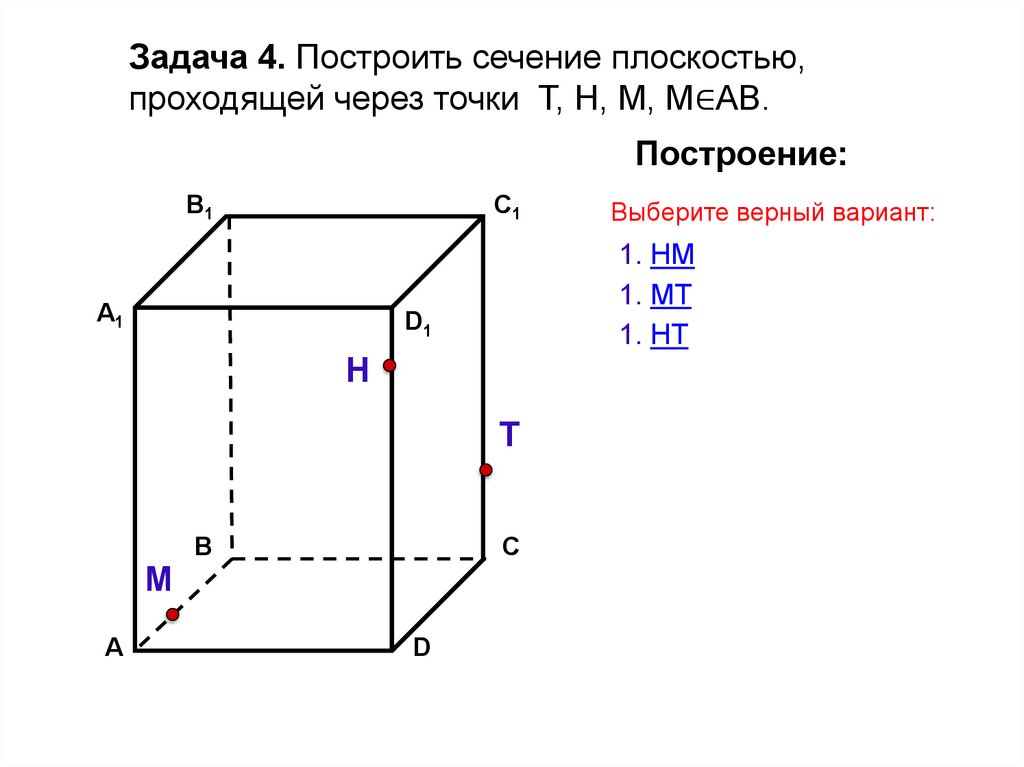
Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
Выберите верный вариант:

14.

Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

15.

Задача 4. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад

16.

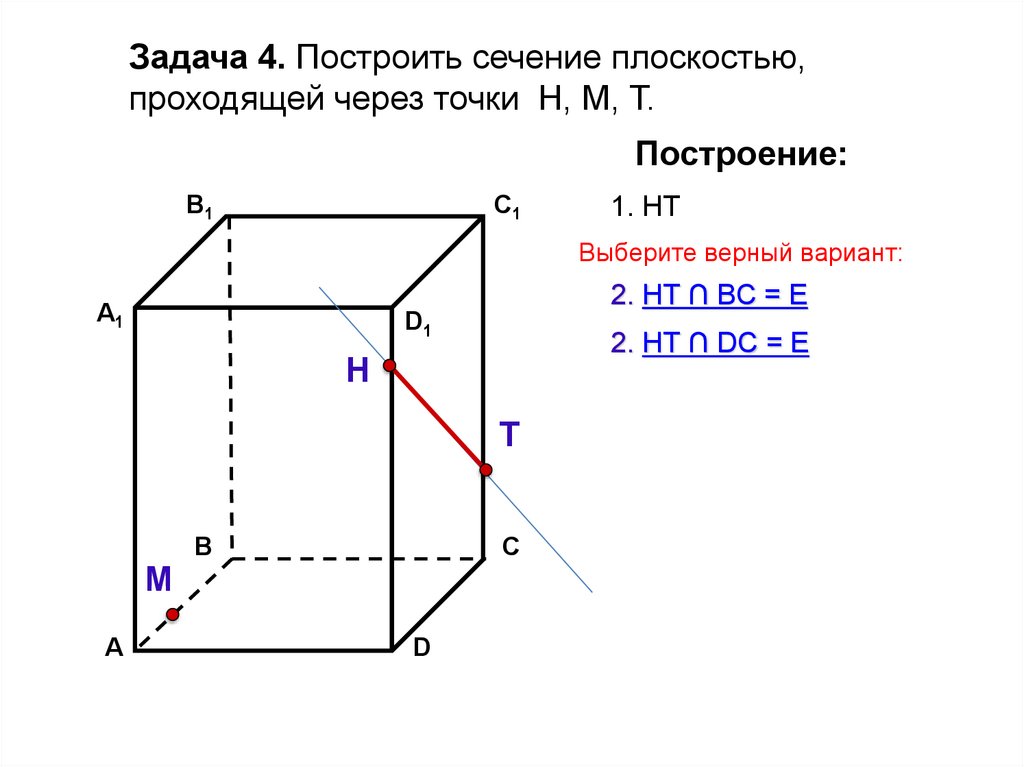
Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D

17.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

18.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е

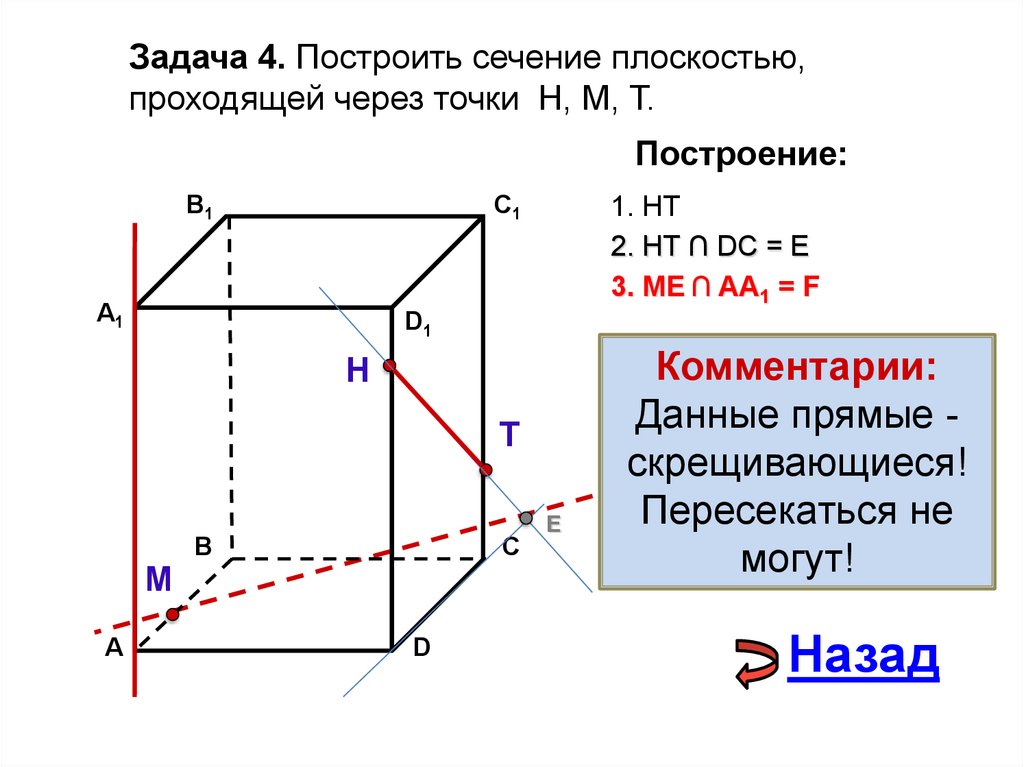
19.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

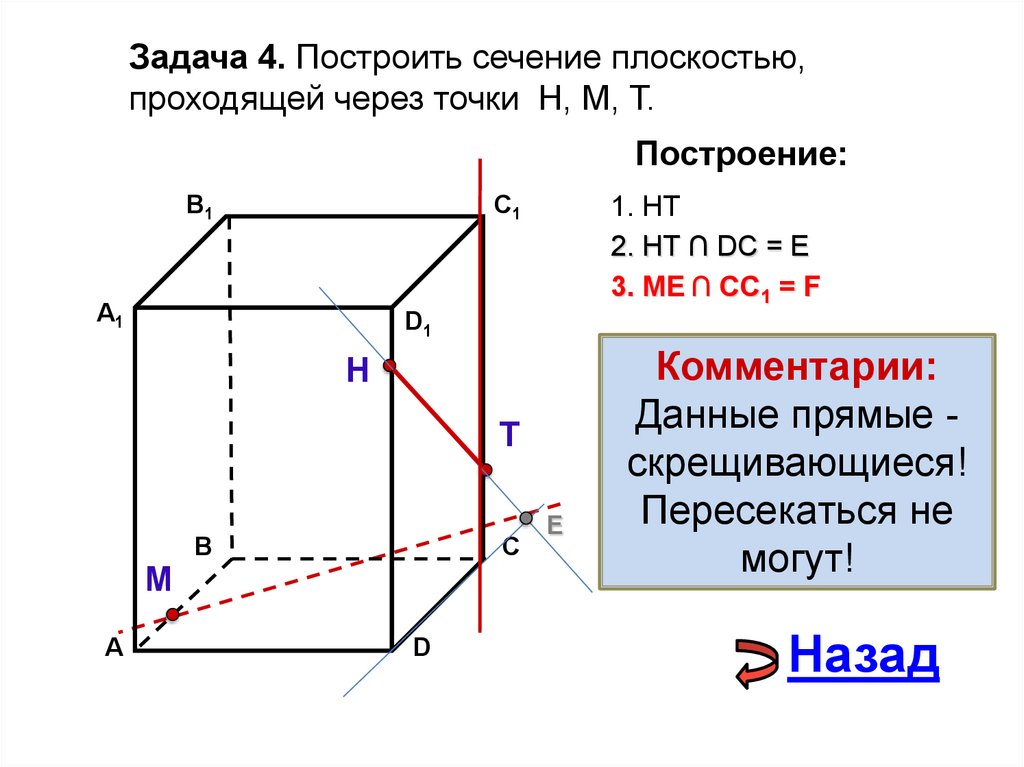
20.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

21.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
4. НF
Н
4. МТ
Т
М
А
В
F
С
D
4. ТF
E

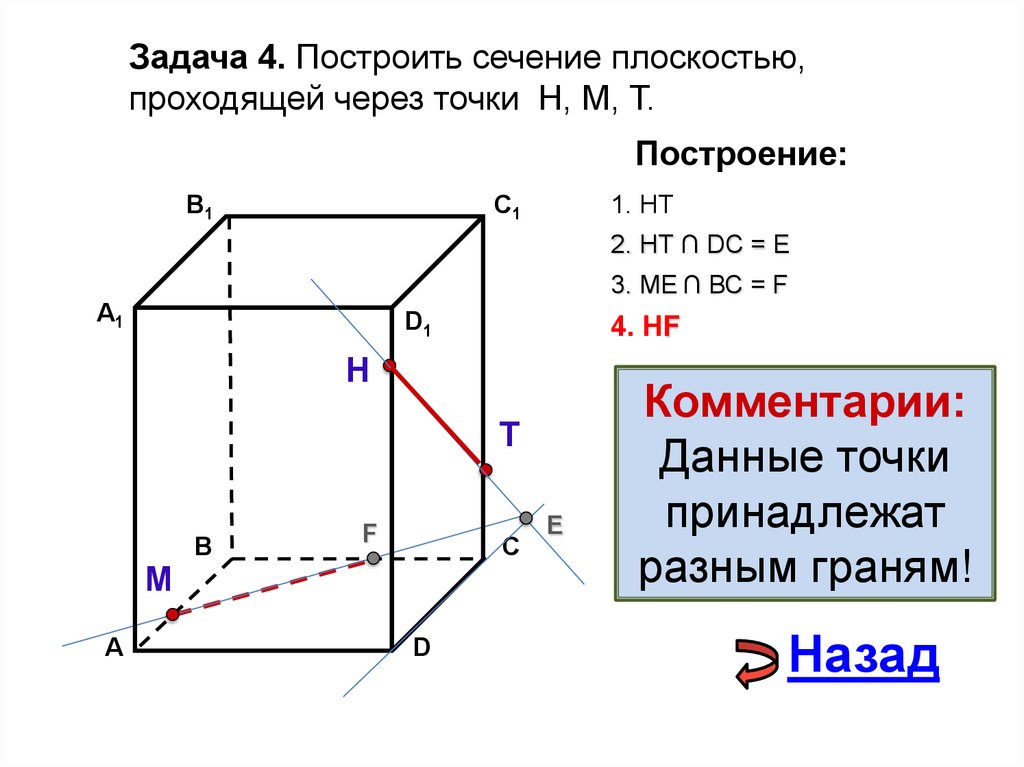
22.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

23.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад

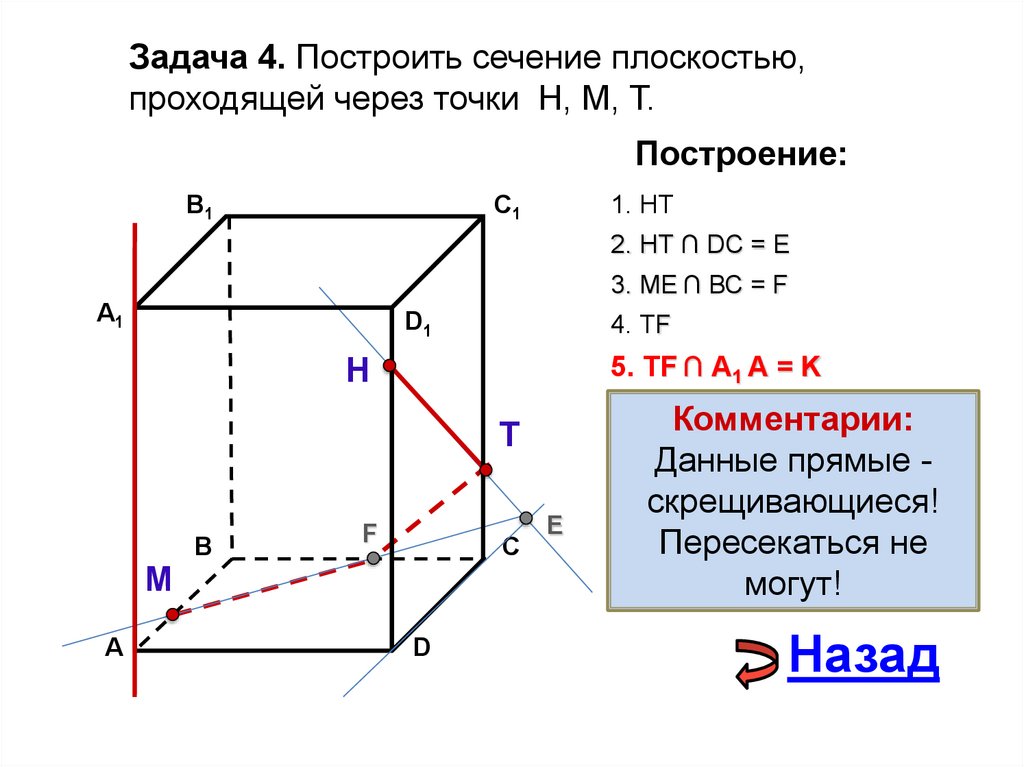
24.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А = K
Т
М
А
В
F
С
D
5. ТF ∩ В1В = K
E

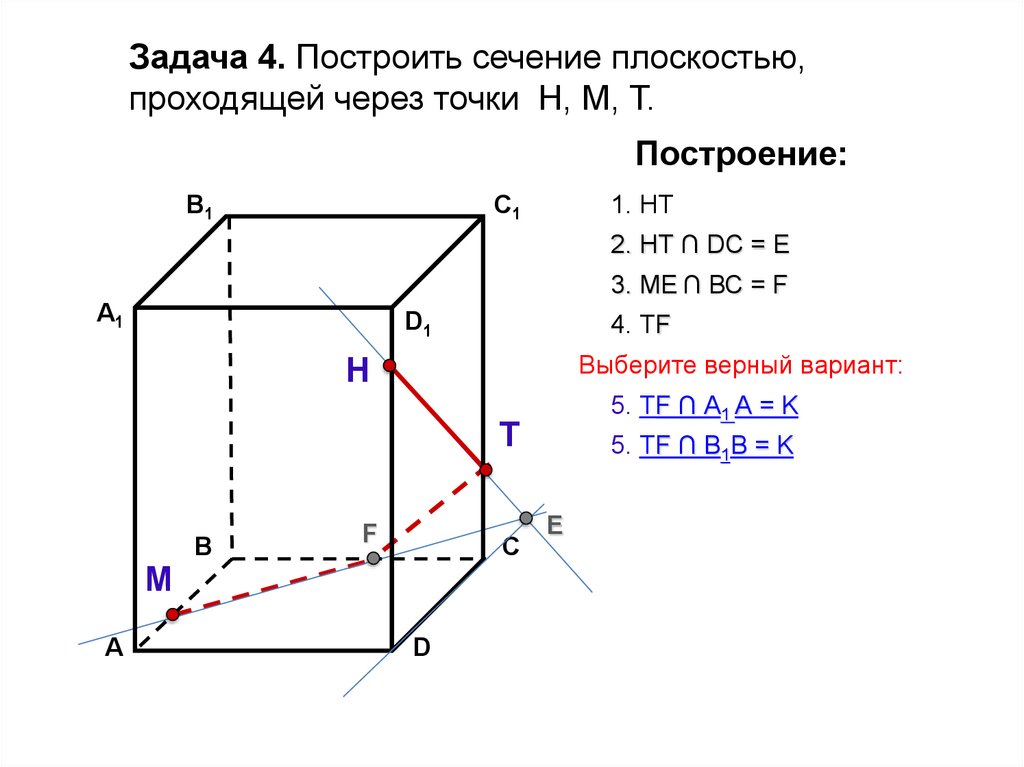
25.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад

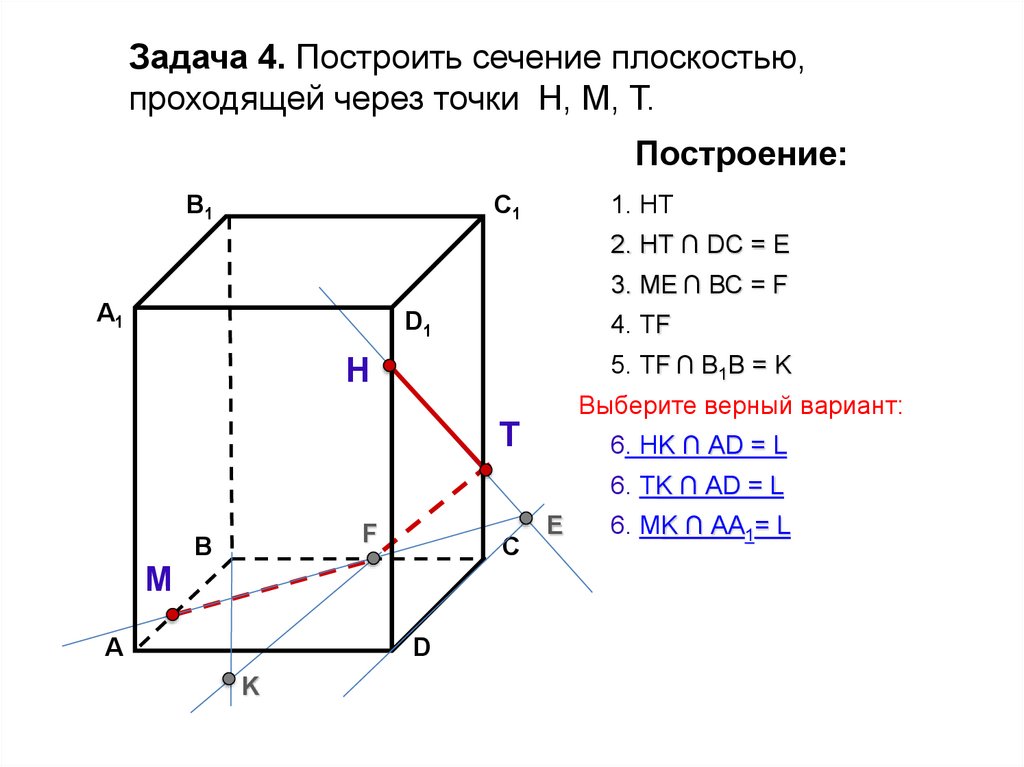
26.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
Выберите верный вариант:
Т
6. НK ∩ АD = L
6. ТK ∩ АD = L
М
F
В
А
С
D
K
E
6. МK ∩ АА1= L

27.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

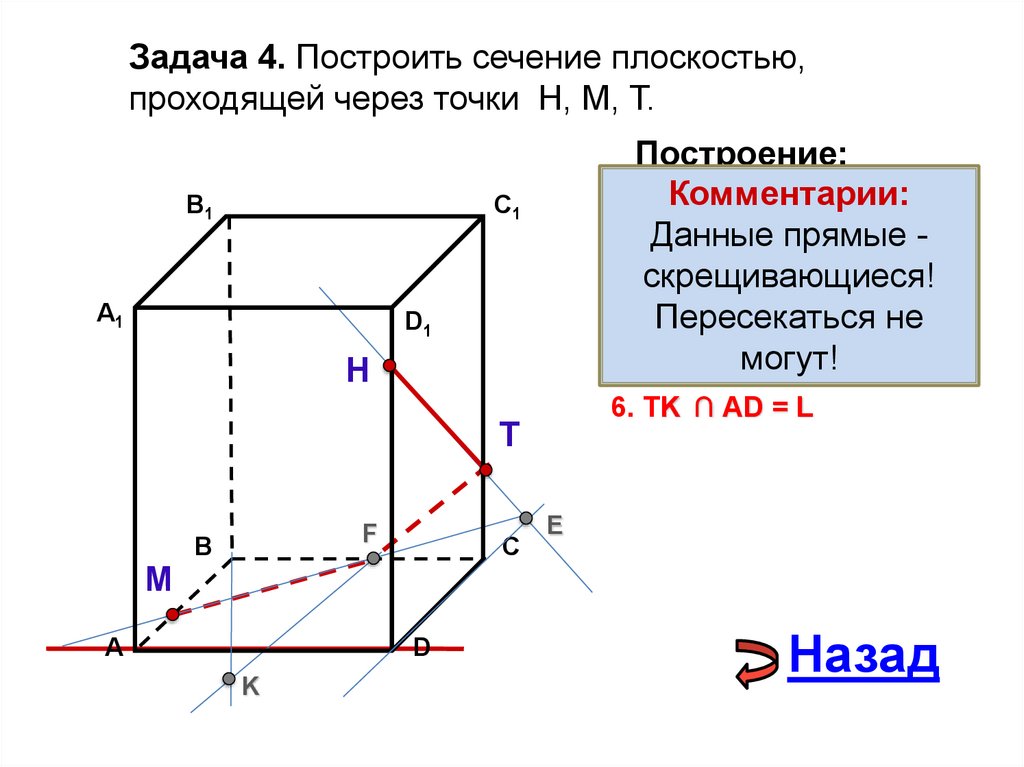
28.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад

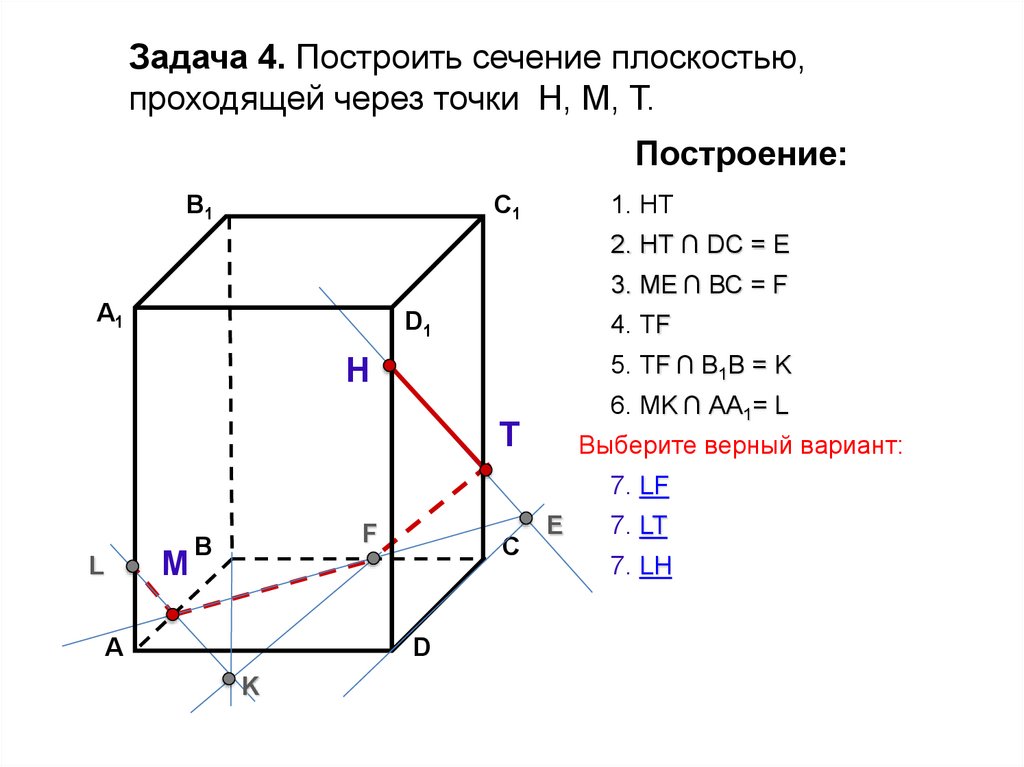
29.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
Выберите верный вариант:
7. LF
М
L
F
В
А
С
D
K
E
7. LT
7. LH

30.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LТ
E
М
А
D
K
Назад

31.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LF
E
М
А
D
K
Назад

32.

Задача 4. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение

33.

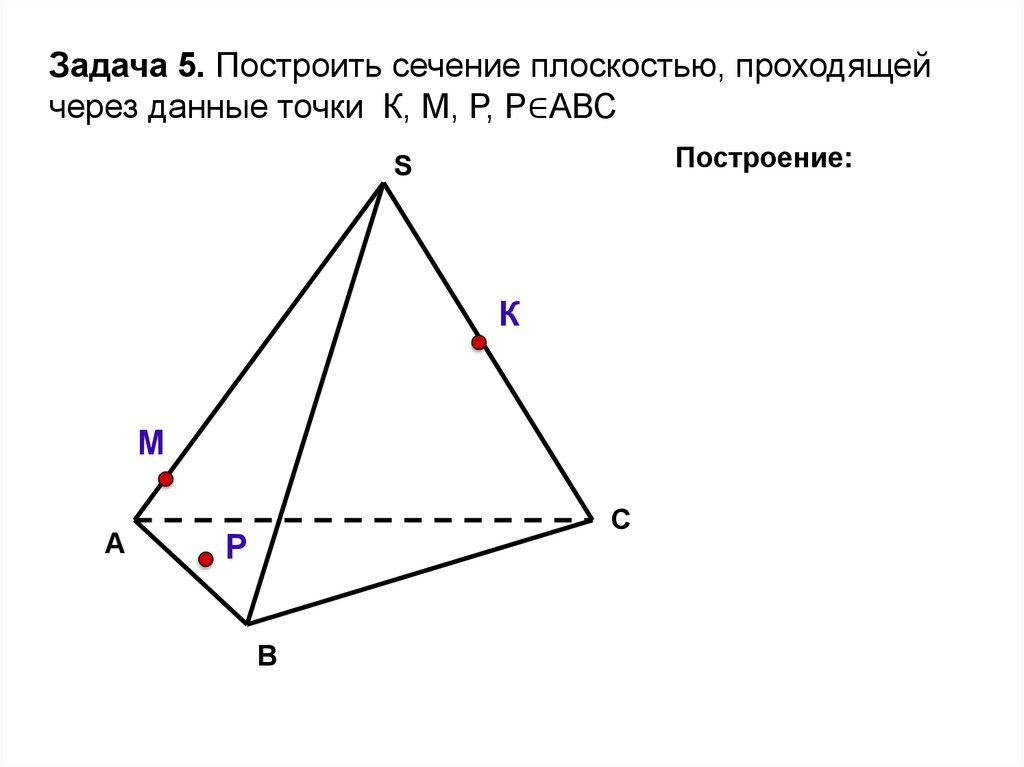
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
S
К
М
А
С
Р
В

34.

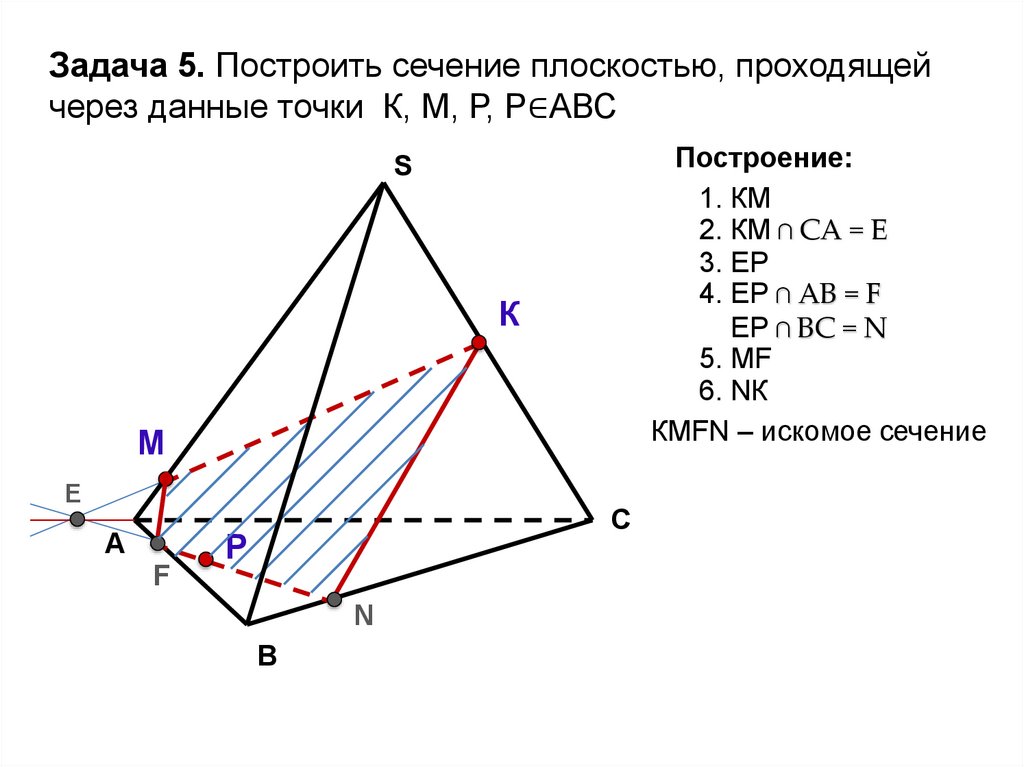
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В