РБФ-сети. НС Хопфилда. НС Кохонена

1.

Лекция 6
РБФ-сети.
НС Хопфилда.
НС Кохонена.

2.

НС – УНИВЕРСАЛЬНЫЙ АППРОКСИМАТОР
Теорема (Колмогоров А.Н., 1957): любую непрерывную функцию m
переменных можно получить с помощью операций сложения, умножения и
суперпозиции из непрерывных функций одного переменного:
F x1, x2 ,..., xm
2 m 1
j 1
m
g j i hij xi ,
i 1
(1)
Теорема (Cybenko G., Funahashi K., Hornik K.M. и др. 1989): любую
непрерывную функцию m переменных можно с любой степенью точности
реализовать с помощью персептрона с одним скрытым слоем, имеющего
достаточное количество нейронов в скрытом слое.
X
НС
Y
Y F X
2

3.

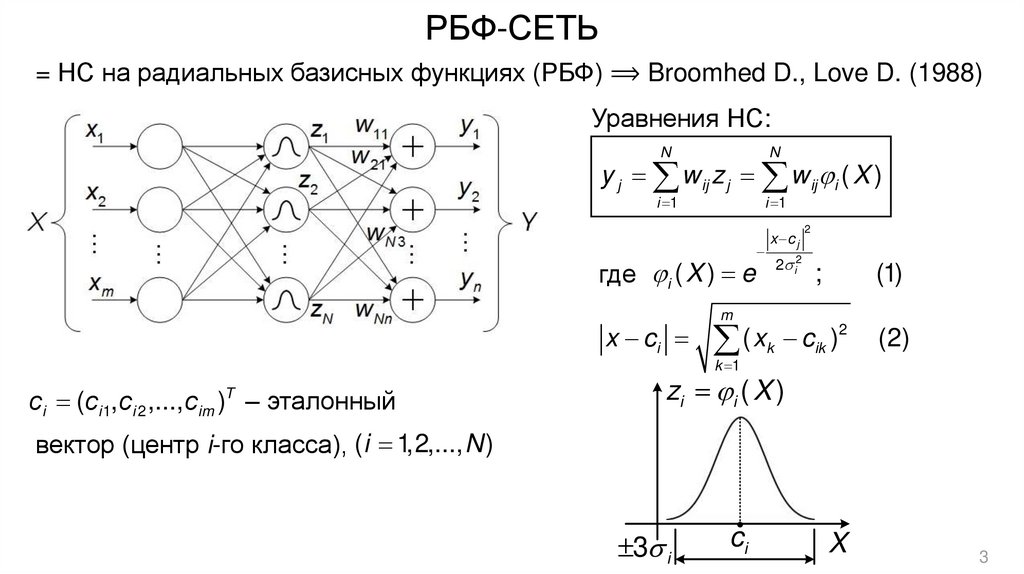
РБФ-СЕТЬ
= НС на радиальных базисных функциях (РБФ) ⟹ Broomhed D., Love D. (1988)
Уравнения НС:
N
N
i 1
i 1
y j w ij z j w ij i ( X )
где i ( X ) e
x ci
сi (ci 1, ci 2 ,..., cim )T – эталонный
x c j
2 i2
2
;
(1)
m
2
(
x
c
)
k ik
(2)
k 1
zi i ( X )
вектор (центр i-го класса), (i 1,2,..., N )
3 i
ci
X
3

4.

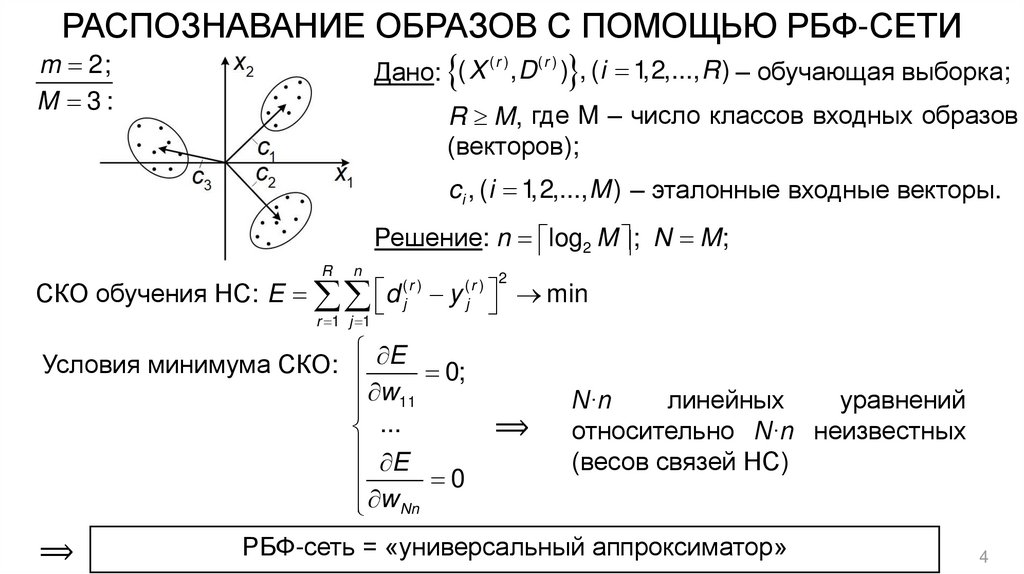
РАСПОЗНАВАНИЕ ОБРАЗОВ С ПОМОЩЬЮ РБФ-СЕТИ
m 2;
M 3:
(r )
(r )
Дано: ( X , D ) , ( i 1,2,..., R ) – обучающая выборка;
R M, где M – число классов входных образов
(векторов);
ci , (i 1,2,..., M ) – эталонные входные векторы.
Решение: n log2 M ; N M;
R
n
СКО обучения НС: E d
r 1 j 1
(r )
j
y
(r ) 2
j
Условия минимума СКО: E 0;
w11
...
E
0
w Nn
⟹
min
⟹
N∙n
линейных
уравнений
относительно N∙n неизвестных
(весов связей НС)
РБФ-сеть = «универсальный аппроксиматор»
4

5.

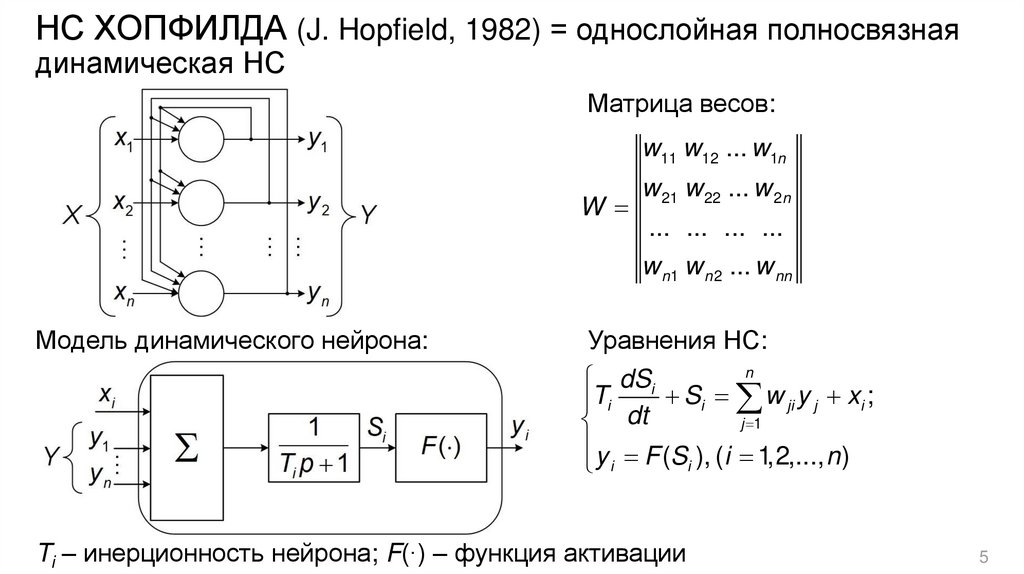
НС ХОПФИЛДА (J. Hopfield, 1982) = однослойная полносвязная
динамическая НС
Матрица весов:
w11 w12 ... w1n
W
w 21 w 22 ... w 2 n
... ... ... ...
w n1 w n 2 ... w nn
Модель динамического нейрона:
Уравнения НС:
n
dSi
Si w ji y j xi ;
Ti
j 1
dt
y F (S ), (i 1,2,..., n )
i
i
Ti – инерционность нейрона; F(∙) – функция активации
5

6.

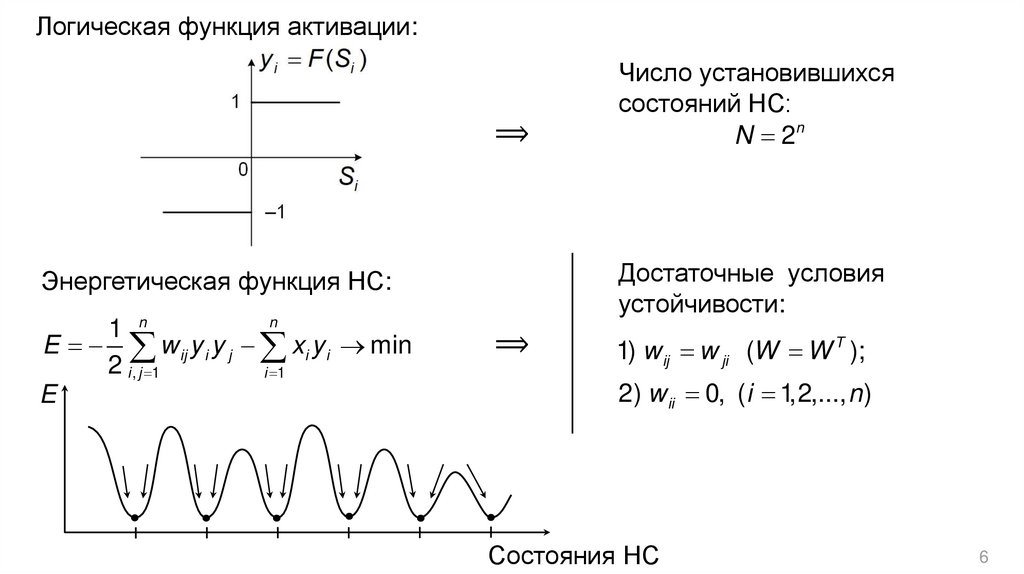
Логическая функция активации:
⟹
Достаточные условия
устойчивости:
Энергетическая функция НС:
n
1 n
E w ij y i y j xi y i min
2 i , j 1
i 1
E
Число установившихся
состояний НС:
N 2n
⟹
1) w ij w ji (W W T );
2) w ii 0, ( i 1,2,..., n )
Состояния НС
6

7.

Обучающая выборка НС: X ( r ) , (r 1,2,..., R ), где xi( r ) 1,1 .
1 R (r )
(r ) T
Правило выбора весов: W X X , т.е. обучение за 1 шаг.
n r 1
Решаемые задачи:
1) ассоциативная
данных);
память
(восстановление
неполных
или
искаженных
2) комбинаторная оптимизация:
F
n
n
a y y b y
i , j 1
ij
i
j
i 1
i
i
min, где y i 1,1 .
⟹ w ij 2aij ; xi bi
7

8.

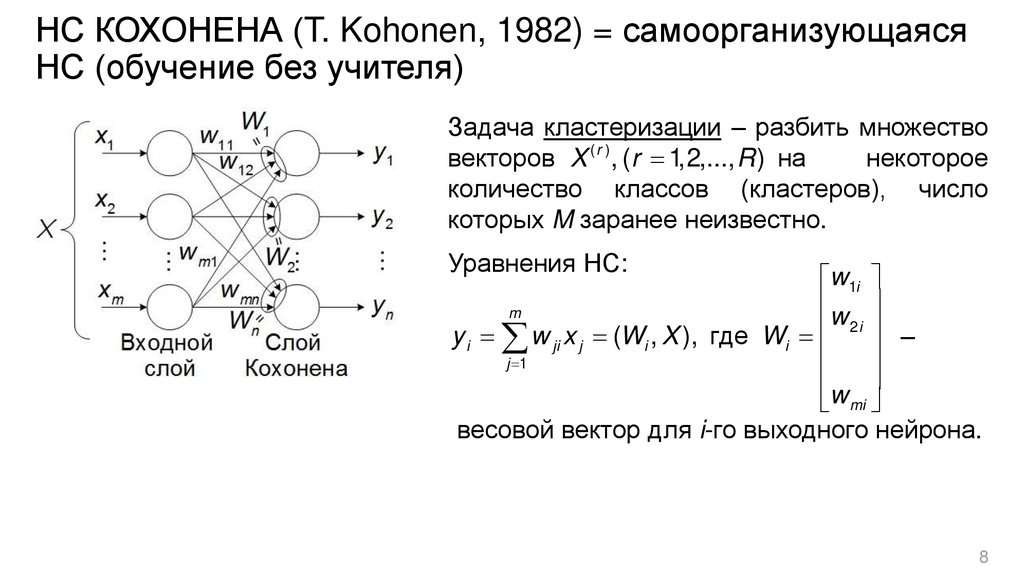
НС КОХОНЕНА (T. Kohonen, 1982) = самоорганизующаяся
НС (обучение без учителя)
Задача кластеризации – разбить множество
векторов X ( r ) , (r 1,2,..., R ) на
некоторое
количество классов (кластеров), число
которых M заранее неизвестно.
Уравнения НС:
w1i
m
w
y i w ji x j (Wi , X ), где Wi 2i –
j 1
w mi
весовой вектор для i-го выходного нейрона.
8

9.

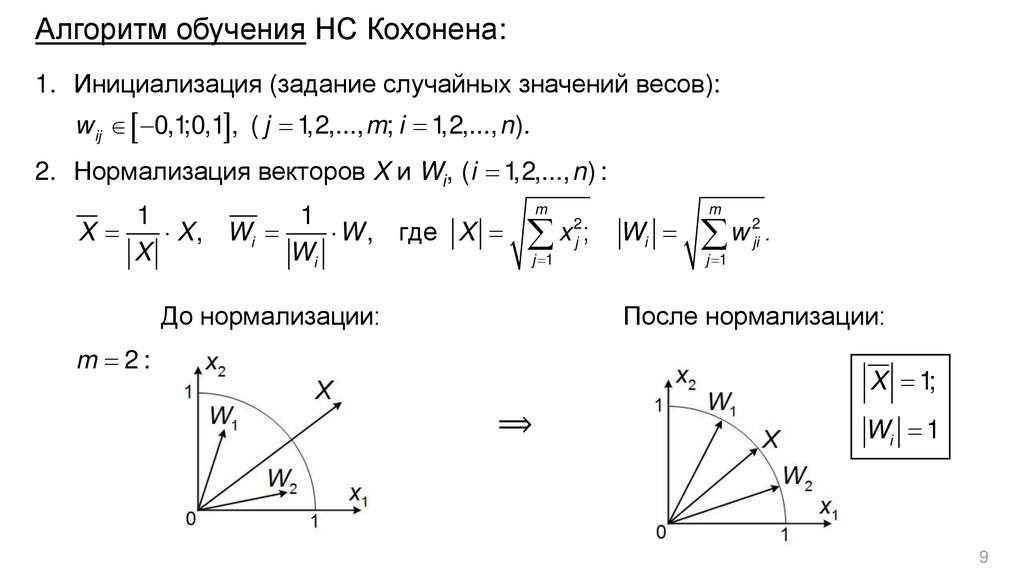
Алгоритм обучения НС Кохонена:
1. Инициализация (задание случайных значений весов):
w ij 0,1;0,1 , ( j 1,2,..., m; i 1,2,..., n ).
2. Нормализация векторов X и Wi, (i 1,2,..., n ) :
1
1
X
X , Wi
W , где X
X
Wi
m
x ;
j 1
До нормализации:
2
j
Wi
m
2
w
ji .
j 1
После нормализации:
m 2:
X 1;
⟹
Wi 1
9

10.

3. Вычисляются выходы НС:
m
y i w ji x j (W i , X ) W i X cos , (i 1,2,..., n ) (1)
j 1
4. Определяется нейрон-победитель, имеющий максимальное значение yi, т.е.
наименьшее удаление вектора весов Wi от входного вектора X:
y e max y i X W e min X W i .
(2)
1 i n
1 i n
5. Настраиваются веса нейрона-победителя
забирает все!» (The Winner Takes All, WTA):
We (k 1) We (k ) X (k ) We (k ) .
по принципу
«Победитель
(3)
6. Повторяются шаги 2-5 для различных входных векторов X ( r ) , (r 1,2,..., R ).
Результат кластеризации
(m 2; M 3) :
(n M ) ‒ количество
«мертвых» нейронов
10