Похожие презентации:
Постоянный ток. Лекция №6
1. Лекция № 6 ПОСТОЯННЫЙ ТОК
621
2. ВОПРОСЫ 17. Электрический ток. Условия существования. Сила тока. Плотность тока. Уравнение непрерывности.
622
3. 18. Электродвижущая сила. Закон Ома. Закон Ома в дифференциальной форме для однородного и неоднородного участка цепи. Закон Ома
длязамкнутой цепи.
19. Работа и мощность тока. КПД.
Закон Джоуля-Ленца. Правила
Кирхгофа.
62
3
4. 17. Электрический ток. Условия существования. Сила тока. Плотность тока. Уравнение непрерывности.
624
5. Электрический ток – упорядоченное движение заряженных частиц. Электрический ток – перенос электрического заряда через некоторую
воображаемуюповерхность.
62
5
6. Для того чтобы в проводнике длительное время существовал электрический ток необходимо: 1) наличие электрических зарядов; 2)
наличие внутри проводниканапряженности электрического поля
(разности потенциалов на его
концах).
62
6
7. Количественной мерой электрического тока является сила тока I. Количество электричества (заряд), протекающее через поперечное
сечение проводника в единицувремени называют силой тока
(измеряется в Амперах), т. е.
dq
I
dt
62
7
8. Когда электрический ток распределен в проводнике неравномерно, то используют понятие вектора плотности тока, модуль которого
равенdI
j
dS
здесь S┴ – поверхность
перпендикулярная движению
электронов или силе тока.
62
8
9. Если известен вектор плотности тока в каждой точке некоторой поверхности S, то можно найти силу тока через эту поверхность как
потоквектора плотности
тока, т. е
I j dS n
вектор
нормали к
где n единичный
поверхности.
За направление вектора j принято
направление упорядоченного
движения положительных зарядов.
62
9
10. Если в проводящей среде, где течет ток, выделить замкнутую поверхность S, то интеграл характеризует весь заряд, выходящий в
Если в проводящей среде, где течетток, выделить замкнутую
поверхность S, то интеграл
j
d
S
n
S
характеризует весь заряд,
выходящий в единицу времени
наружу из объема V, охваченного
поверхностью S.
62
10
11. Заряд, который находится в объёме V, охваченного поверхностью S
q ρdVV
62
11
12. На основании закона сохранения заряда этот интеграл равен убыли заряда в единицу времени внутри объема V, т. е.
dqj
d
S
n
dt
S
62
12
13. Согласно закону сохранения электрического заряда Эту формулу называют уравнением непрерывности (интегральная форма).
Согласно закону сохраненияэлектрического заряда
j dS n d ρdV ρ dV
S
dt V
V t
Эту формулу называют
уравнением непрерывности
(интегральная форма).
62
13
14. По теореме Остроградского-Гаусса или Это уравнением непрерывности (дифференциальная форма).
По теореме Остроградского-Гауссаρ
V j dV V t dV
или
ρ
( j )
t
Это уравнением непрерывности
(дифференциальная форма).
62
14
15. Для постоянного тока I = сonst, т. е. Следовательно, уравнение непрерывности для постоянного тока принимает вид
Для постоянного тока I = сonst, т. е.dq
0.
dt
Следовательно, уравнение
непрерывности для постоянного тока
принимает вид
j dS n 0
S
62
( j ) 0
15
16. Отсюда следует вывод, что вектор J не имеет источников, линии тока нигде не начинаются и нигде не заканчиваются, они всегда
замкнуты.62
16
17.
6217
18. 18. Электродвижущая сила. Закон Ома. Закон Ома в дифференциальной форме для однородного и неоднородного участка цепи. Закон Ома
для замкнутой цепи.62
18
19. Под действием кулоновских сил электростатического поля в проводниках происходит выравнивание потенциалов на концах проводников
( = 0)и ток прекращается.
62
19
20. Поэтому для поддержания длительное время в цепи постоянного тока, наряду с участками, где положительные носители тока движутся
в сторонууменьшения потенциала, должны
иметься участки, на которых перенос
этих зарядов происходит в сторону
возрастания потенциала, т. е. против
сил электрического поля.
62
20
21.
6221
22. Это возможно лишь под действием сил не электростатического происхождения. Такие силы называют сторонними. Физическая природа
сторонних силможет быть самой разнообразной:
механической, химической,
световой, магнитной и т. д.
62
22
23. Величина, равная работе сторонних сил, по перемещению единичного положительного заряда по замкнутому контуру, называется
электродвижущей силой(измеряется в Вольтах – В)
A
q
62
23
24. Найдём работу сторонних сил по перемещению положительного заряда Fст = E*·q, здесь E* – напряжённость поля сторонних сил, q –
заряд.2
*
A12 Fст d q E d q 12
2
1
1
62
24
25. Для электродвижущей силы получится следующее выражение для участка цепи 1-2 и для замкнутой цепи, соответственно:
*E d
*
12 E d
2
1
62
25
26. Работа сил электростатического поля по перемещению положительного заряда Работа сил электростатического поля по перемещению
Работа сил электростатическогополя по перемещению
положительного заряда
2
2
A12 F d q E d q 1 2
1
1
Работа сил электростатического
поля по перемещению
положительного заряда по
замкнутому контуру
равна
нулю
A F d 0
62
26
27. Суммарно, работа по перемещению заряда на участке 1-2 складывается из работы сторонних сил и работы силы электростатического
Суммарно, работа по перемещениюзаряда на участке 1-2 складывается
из работы сторонних сил и работы
силы 2электростатического поля
A12 F Fст d q φ1 φ 2 q
1
62
27
28. Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного
заряда, называетсяпадением напряжения или просто
напряжением на данном участке
цепи
U12 φ1 φ2 12
62
28
29. Участок с ЭДС называется неоднородным. Участок без ЭДС называется однородным. В случае однородного участка говорят о разности
потенциаловU12 φ1 φ2
62
29
30. Закон Ома для однородного участка, для неоднородного участка и для замкнутой цепи, соответственно: (r – внутреннее
сопротивлениеисточника ЭДС)
φ U
I
R
R
φ1 φ 2 12
I
R
62
I
R r
30
31. Закон Ома для однородного участка, и для неоднородного участка в дифференциальной форме, соответственно:
j σE*
j σ( E E )
62
31
32. здесь σ – удельная электропроводность, удельная электропроводимость равна σ = 1/ρ, ρ – удельное электросопротивление.
Сопротивление определяется черезудельное сопротивление, длину
проводника ℓ и поперечное сечение
проводника S:
R ρ
S
62
32
33. Величины измеряются: Сопротивление R – Ом ; Проводимость – Ом = 1/См ; Удельная электропроводность σ – См/м = 1/(Ом·м);
Удельное электросопротивлениеρ – м/См = Ом·м.
62
33
34. Возьмём закон Ома в дифференциальной форме для неоднородного участка
*j σ( E E )
62
34
35. Проинтегрируем по длине с учётом того, что силу тока можно выразить следующим способом I = j · dS и с учётом того, что удельную
электропроводность можно заменитьудельным сопротивлением σ = 1/ρ.
62
35
36.
*( j d )
(
E
d
)
(
E
d
)
σ
1
1
1
2
2
2
l
l
j Iρ IR φ1 φ 2 12
σ
S
62
36
37. Таким образом, из закона Ома для неоднородного участка цепи в дифференциальной форме получили закон Ома для неоднородного
участка цепи.φ1 φ 2 12
I
R
62
37
38. Если взять замкнутый участок (точка «1» совпадает с точкой «2») φ1 = φ2, то получим Закон Ома для замкнутого участка цепи:
IR r
62
38
39.
6239
40. 19. Работа и мощность тока. КПД. Закон Джоуля-Ленца. Правила Кирхгофа.
6240
41. Мощность электрического тока
AP UI φ1 φ 2 12 I
t
A
P UI φ1 φ 2 I
t
62
41
42. Удельная мощность электрического тока (в дифференциальной форме для неоднородного и однородного участков)
*2
Pуд P V j ( E E ) ρj
2
2
Pуд P V j E σE ρj
62
42
43. Закон Джоуля-Ленца: в случае, когда проводник неподвижен и химических превращений в нём нет, работа тока идёт на нагревание:
Q A UIt I Rt2
62
43
44. Закон Джоуля-Ленца для переменного тока:
t2
Q I t Rdt
0
62
44
45. Удельная тепловая мощность (в элементарном объёме в виде цилиндра длиной dℓ и поперечным сечением dS), закон Джоуля-Ленца в
дифференциальной форме:dl
2
2
dQ I Rt ρ jdS dt ρj dVdt
dS
2
dQ
2
2
dQуд
ρj jE σE
dVdt
62
45
46. С учётом законов Ома получим выражение для КПД источника тока
2PR
I R
R
η
2
Pполная I R r R r
62
46
47. Правила Кирхгофа.
6247
48. При расчёте сложных электрических цепей значительно проще использовать правила Кирхгофа, чем законы Ома. Первое правило
КирхгофаАлгебраическая сумма токов в узле
равна нулю,
N
Ik 0
k 1
62
48
49. Узлом называют соединение не менее трех проводов. Условились считать, токи подходящие к узлу положительными, а отходящие –
отрицательными(или наоборот).
62
49
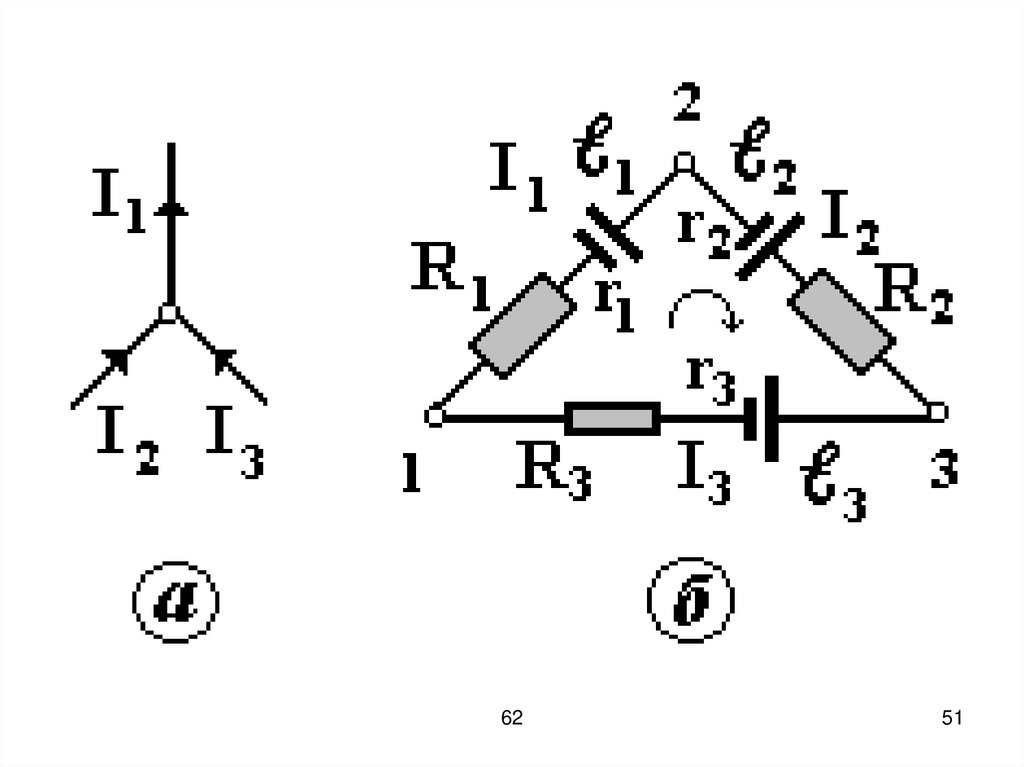
50. Например, на рисунке «а», уравнение, составленное по первому правилу Кирхгофа, запишется в виде: I2 + I3 I1 = 0. Первое
Например, на рисунке «а»,уравнение, составленное
по первому правилу Кирхгофа,
запишется в виде:
I2 + I3 I1 = 0.
Первое правило Кирхгофа является
следствием условия непрерывности
для постоянного тока
(стационарных токов).
62
50
51.
6251
52. Второе правило Кирхгофа: Алгебраическая сумма произведений сил токов на сопротивление отдельных участков произвольного
замкнутого контура (сумма падениянапряжения) равна алгебраической
сумме ЭДС, действующих на этих
участках в замкнутом контуре:
I R
N
k 1
N
k
k
m 1
62
m
52
53. Второе правило Кирхгофа применимо к любому замкнутому контуру разветвленной цепи. Выделим замкнутый контур, состоящий,
например, из трехнеоднородных участков цепи
(рисунок «б»).
62
53
54.
6254
55. При составлении уравнений по правилам Кирхгофа необходимо выполнить ряд простых условий. 1) выбрать направление обхода в
разветвленной цепи общее для всехзамкнутых контуров по часовой, или
против часовой стрелки;
62
55
56. 2) указать стрелками предположительное направление токов от узла до узла с соблюдением условия непрерывности; 3) указать
полярность на зажимахисточников ЭДС;
4) определить число узлов и
замкнутых контуров;
62
56
57. 5) если направление обхода контура совпадает с выбранным направлением тока, то произведение IR берут со знаком плюс; если же
направление тока противоположнонаправлению обхода, то это
произведение берут со знаком
минус;
62
57
58. 6) если ЭДС повышает потенциал в направлении обхода по контуру (внутри источника ток течет от клеммы минус к клемме плюс), то
ее надо брать со знаком плюс;если ЭДС понижает потенциал,
то ее берут со знаком минус;
62
58
59. 7) если в разветвленной цепи имеется n узлов, то число независимых уравнений, составленных по первому правилу Кирхгофа равно: n
– 1;62
59
60. 8) при числе замкнутых контуров равном m, число независимых уравнений, составленных по второму правилу Кирхгофа равно: m – (n –
1),т. е. число независимых уравнений
должно равняться наименьшему
числу разрывов, которые следует
сделать в цепи, чтобы нарушить все
контуры;
62
60
61. 9) если в результате вычислений после решения системы составленных уравнений окажется, что какой-то ток отрицательный, то его
истинное направление в цепипротивоположно выбранному
направлению.
62
61
62. 10) общее число составленных уравнений по первому и второму правилам Кирхгофа должно равняться числу неизвестных в данной
задаче.62
62
63.
6263











































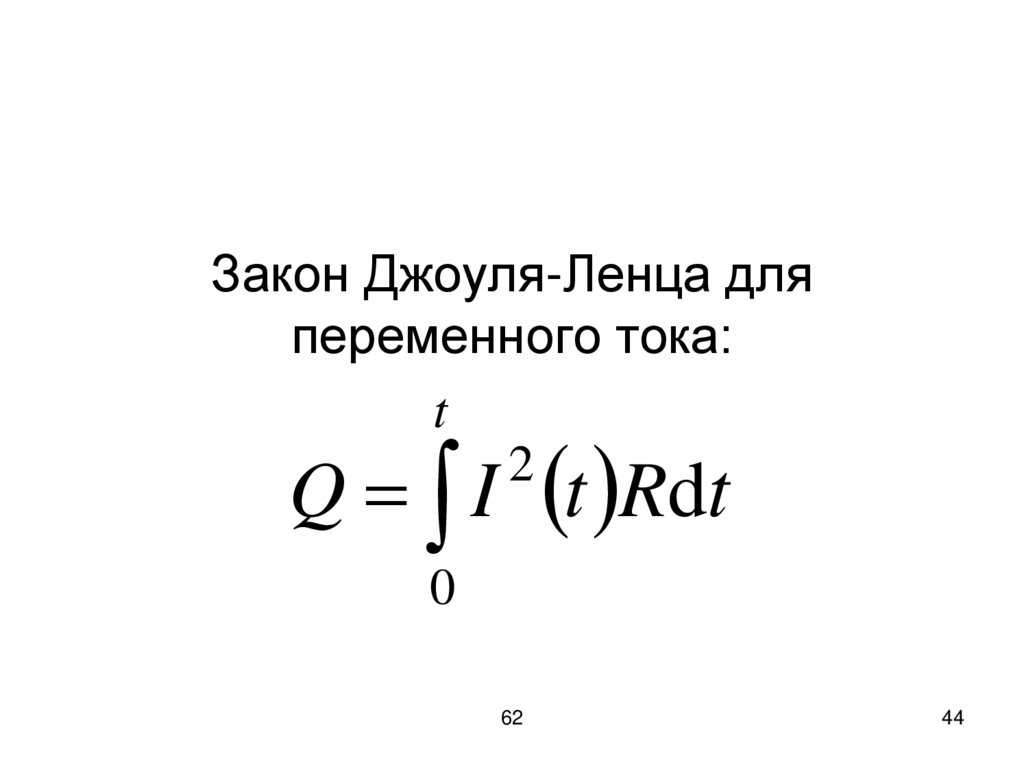


















 Физика
Физика








