Конус. Сечения конической поверхности. Площадь поверхности конуса

1. Конус

Преподаватель: Дағысқызы Ж

2. План урока

Историческая справка
Определение прямой круговой
конической поверхности
Сечения конической поверхности
Определение прямого кругового конуса
Площадь поверхности конуса
Сечения конуса
Усеченный конус
Вопросы

3. Историческая справка

Конус в переводе с греческого «konos» означает
«сосновая шишка».
С конусом люди знакомы с глубокой древности. В
1906 году была обнаружена книга Архимеда (287–
212 гг. до н. э.) «О методе», в которой дается
решение задачи об объеме общей части
пересекающихся цилиндров.
Архимед приписывает честь открытия этого
принципа Демокриту (470–380 гг. до н. э.) –
древнегреческому философу-материалисту.
С помощью этого принципа Демокрит получил
формулы для вычисления объема пирамиды и
конуса.

4. Определение конической поверхности

Множество всех прямых
пространства, проходящих через
некоторую точку S и точки линии
g, называют конической
поверхностью.
Точка S называется вершиной
конической поверхности, линия
g – направляющей, а все
линии, проходящие через S и
точки линии g, –
образующими этой
поверхности.
S
g

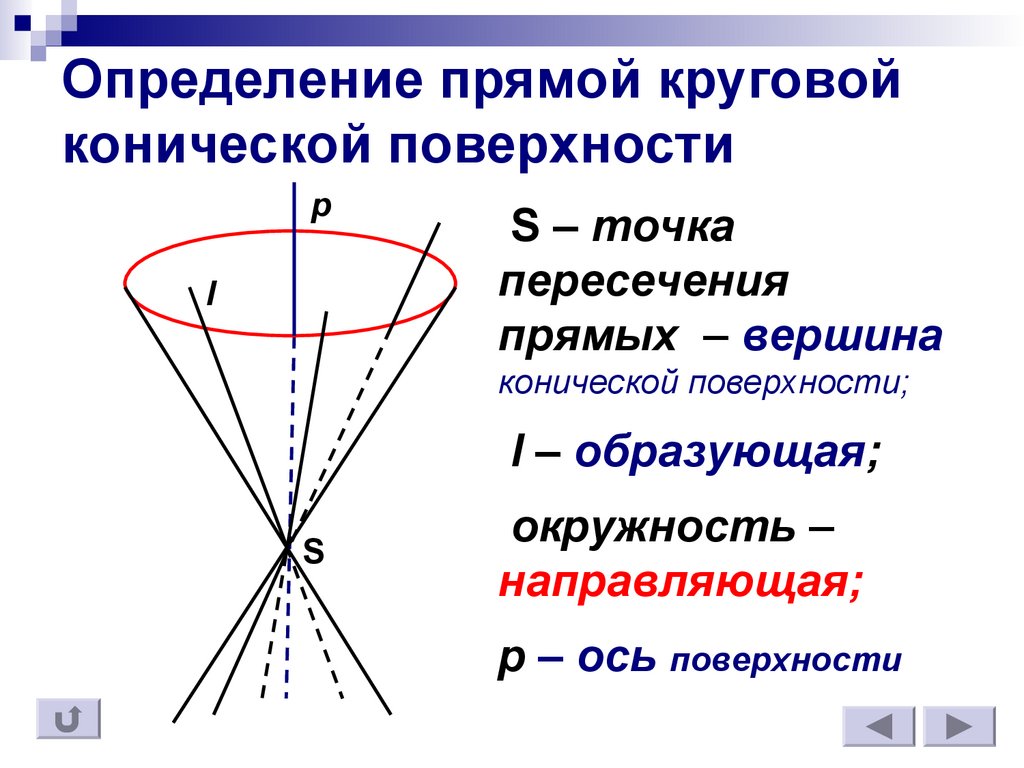
5. Определение прямой круговой конической поверхности

p
l
S – точка
пересечения
прямых – вершина
конической поверхности;
l – образующая;
S
окружность –
направляющая;
p – ось поверхности

6.

Если плоскость проходит через
вершину конической
поверхности, то она пересекает
эту поверхность
либо в одной точке;
либо по двум образующим;
либо имеет с поверхностью
одну общую образующую, т.е.
касается данной поверхности

7. Определение прямого кругового конуса

вершина
Тело, ограниченное
прямой круговой
конической
поверхностью,
вершиной этой
поверхности и
плоскостью
перпендикулярной оси
данной поверхности
наз. прямым
ось
(высота)
боковая
поверхность
круговым конусом
основание

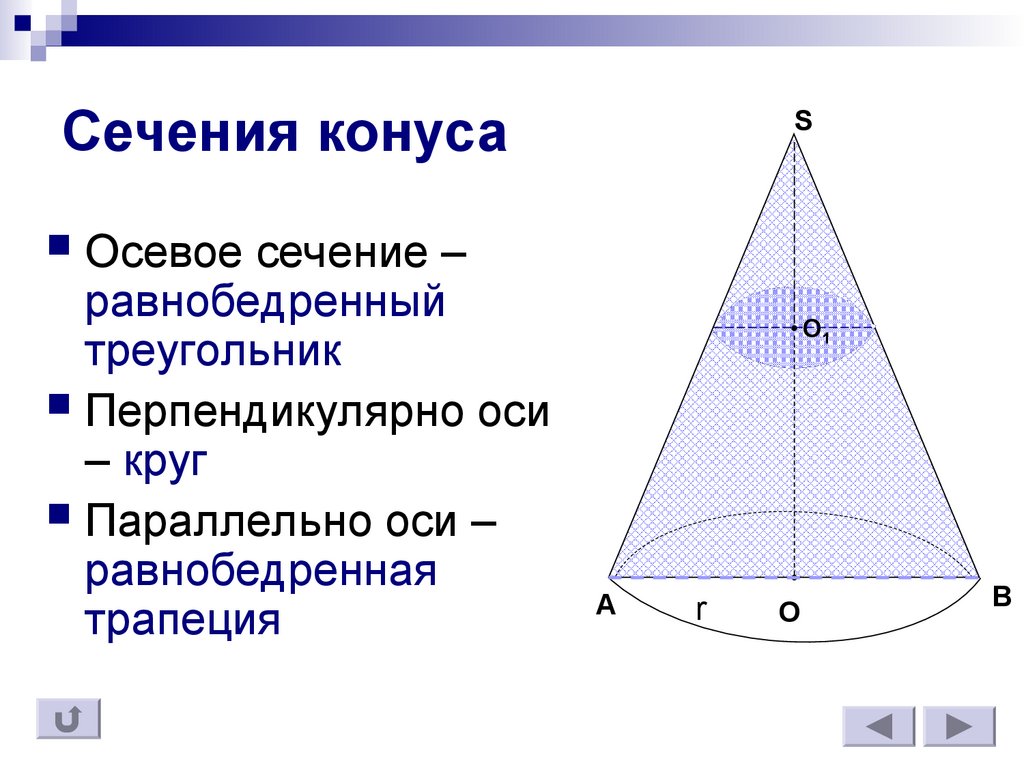
8. Сечения конуса

Осевое сечение –
равнобедренный
треугольник
Перпендикулярно оси
– круг
Параллельно оси –
равнобедренная
трапеция
S
O1
A
r
O
B

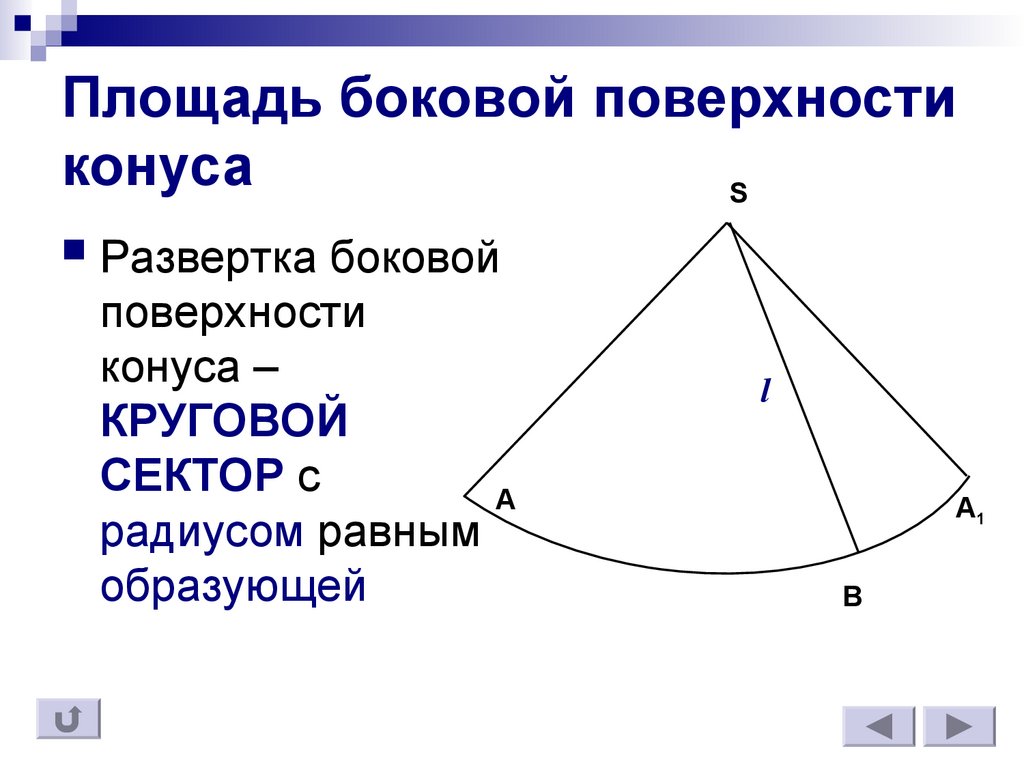
9. Площадь боковой поверхности конуса

S
Развертка боковой
поверхности
конуса –
КРУГОВОЙ
СЕКТОР с
A
радиусом равным
образующей
l
A1
B

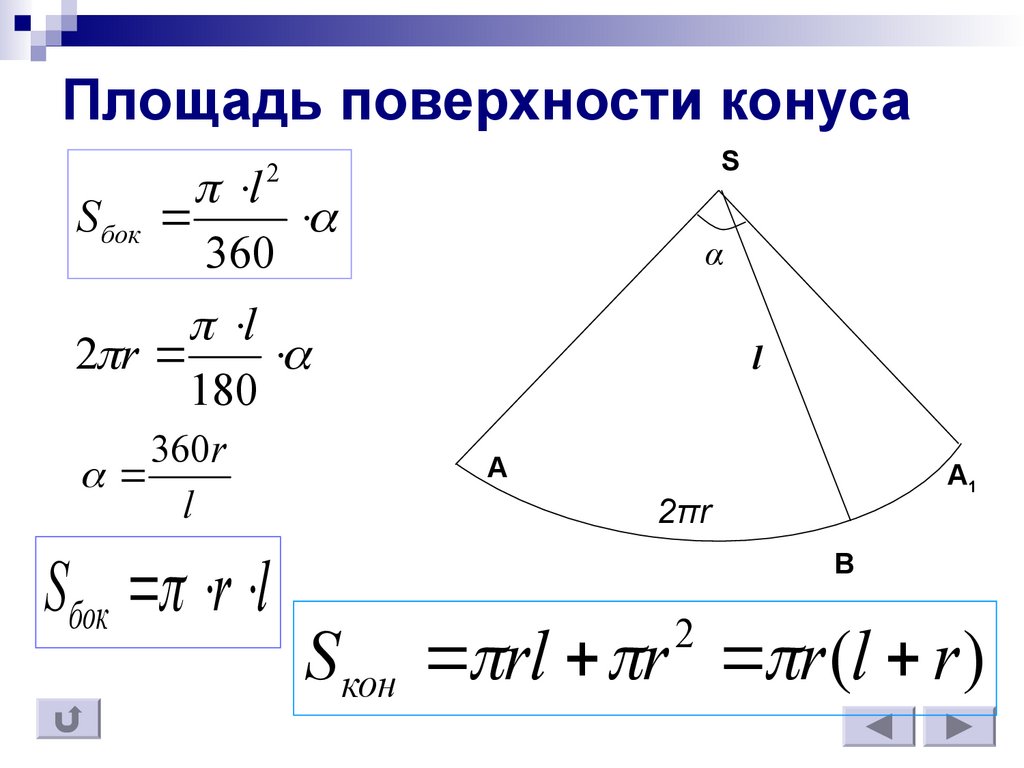
10. Площадь поверхности конуса

S
2
l
S бок
360
l
2 r
180
360r
l
Sбок r l
α
l
A
A1
2πr
B
2
S кон rl r r (l r )

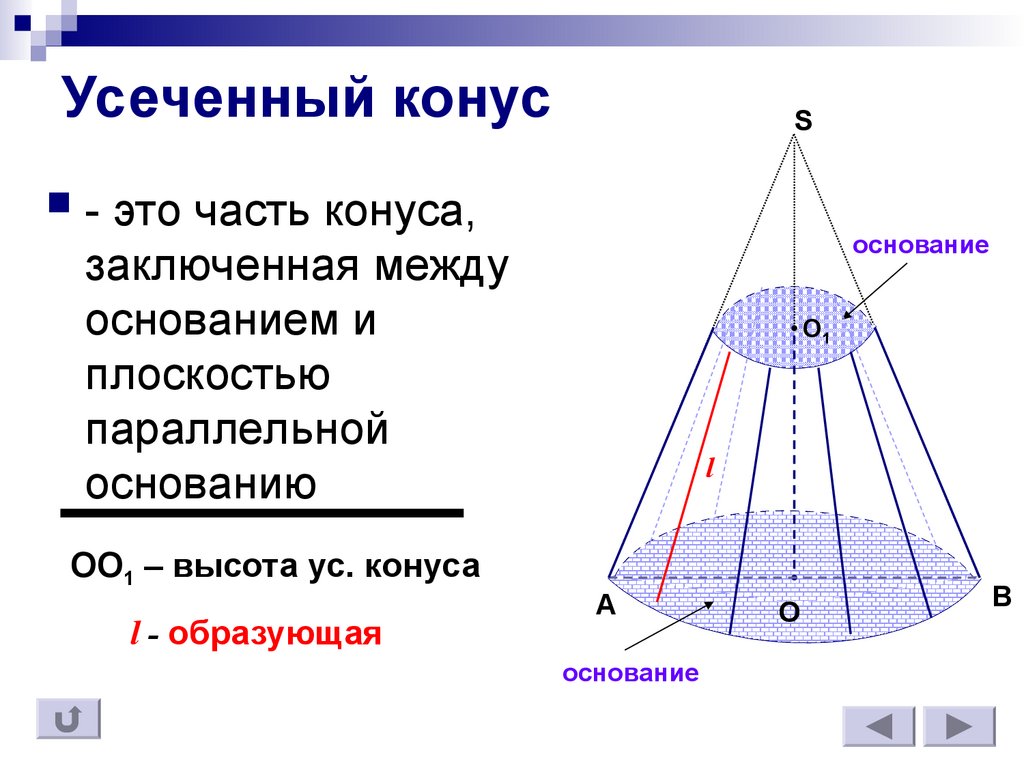
11. Усеченный конус

S
- это часть конуса,
заключенная между
основанием и
плоскостью
параллельной
основанию
ОО1 – высота ус. конуса
l - образующая
основание
O1
l
A
основание
O
B

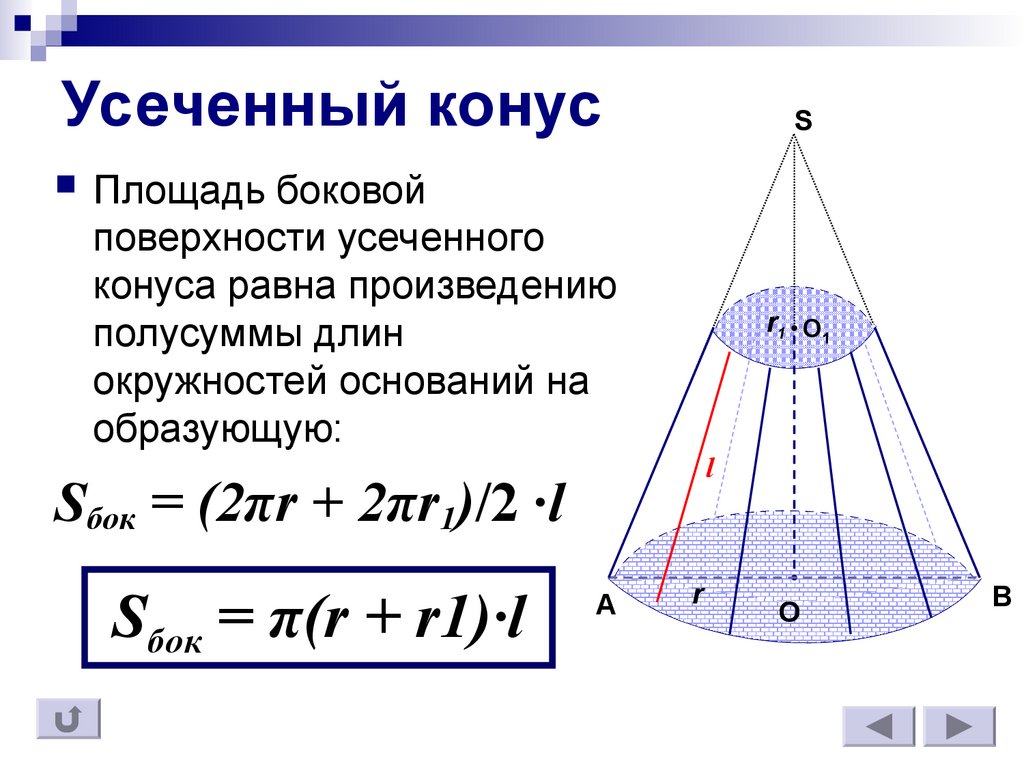
12. Усеченный конус

S
Площадь боковой
поверхности усеченного
конуса равна произведению
полусуммы длин
окружностей оснований на
образующую:
r1 O 1
l
Sбок = (2πr + 2πr1)/2 ·l
Sбок = π(r + r1)·l
A
r
O
B

13. Вопросы для закрепления

1.
2.
3.
4.
5.
6.
Дайте определение прямой круговой
конической поверхности.
Что называется: а) вершиной;
б) образующей;
в) осью конической поверхности?
Какая плоскость наз. касательной к
конической поверхности?
Какие кривые могут получиться в
сечении конической поверхности
плоскостью?
Дайте определение прямого кругового
конуса.
Какой конус наз. усеченным?