Похожие презентации:
Понятие конуса. Площадь поверхности конуса
1.
2.
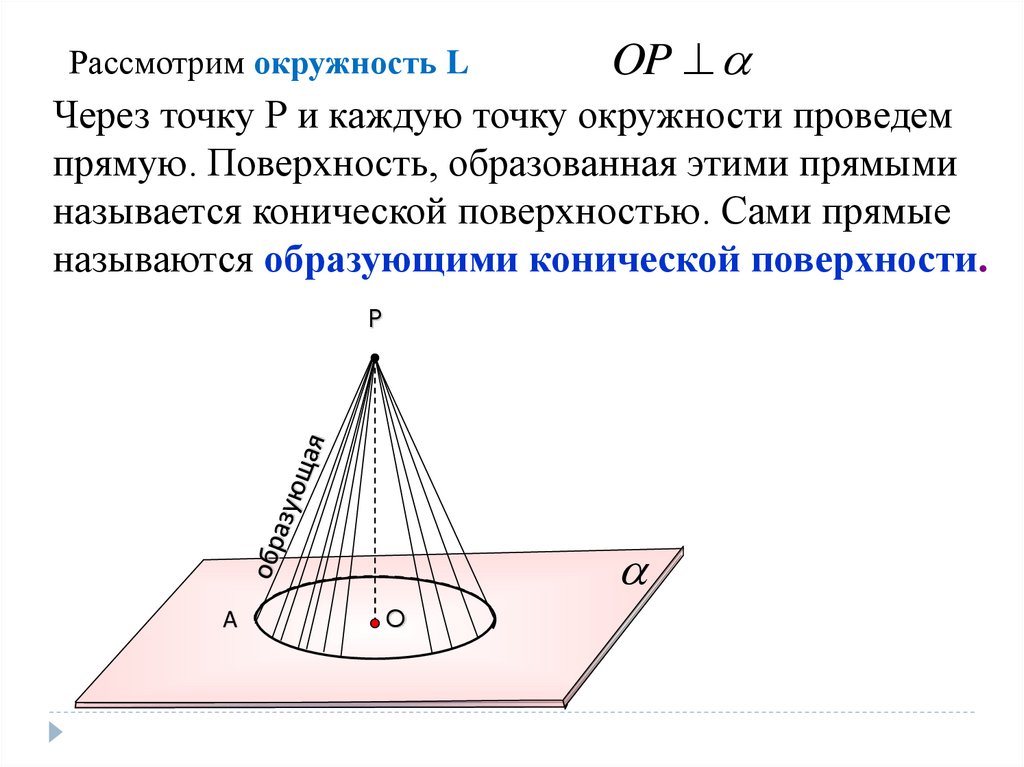
Рассмотрим окружность LOP
Через точку Р и каждую точку окружности проведем
прямую. Поверхность, образованная этими прямыми
называется конической поверхностью. Сами прямые
называются образующими конической поверхности.
P
А
O
3.
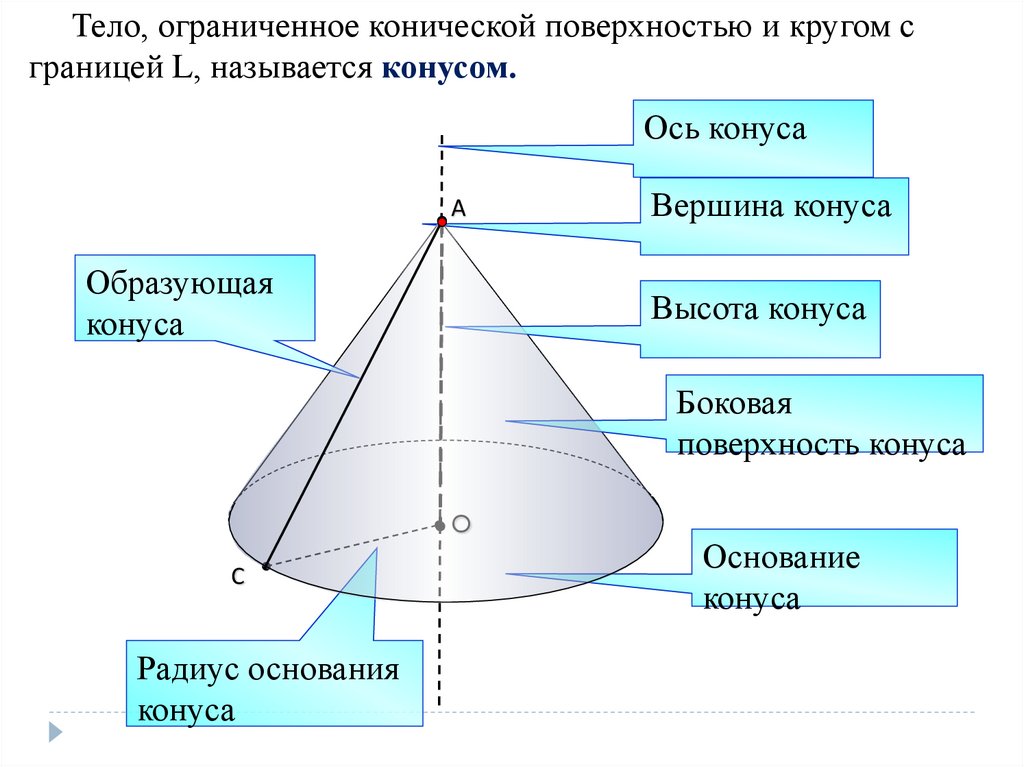
Тело, ограниченное конической поверхностью и кругом сграницей L, называется конусом.
Ось конуса
А
Образующая
конуса
Вершина конуса
Высота конуса
Боковая
поверхность конуса
O
С
Радиус основания
конуса
Основание
конуса
4.
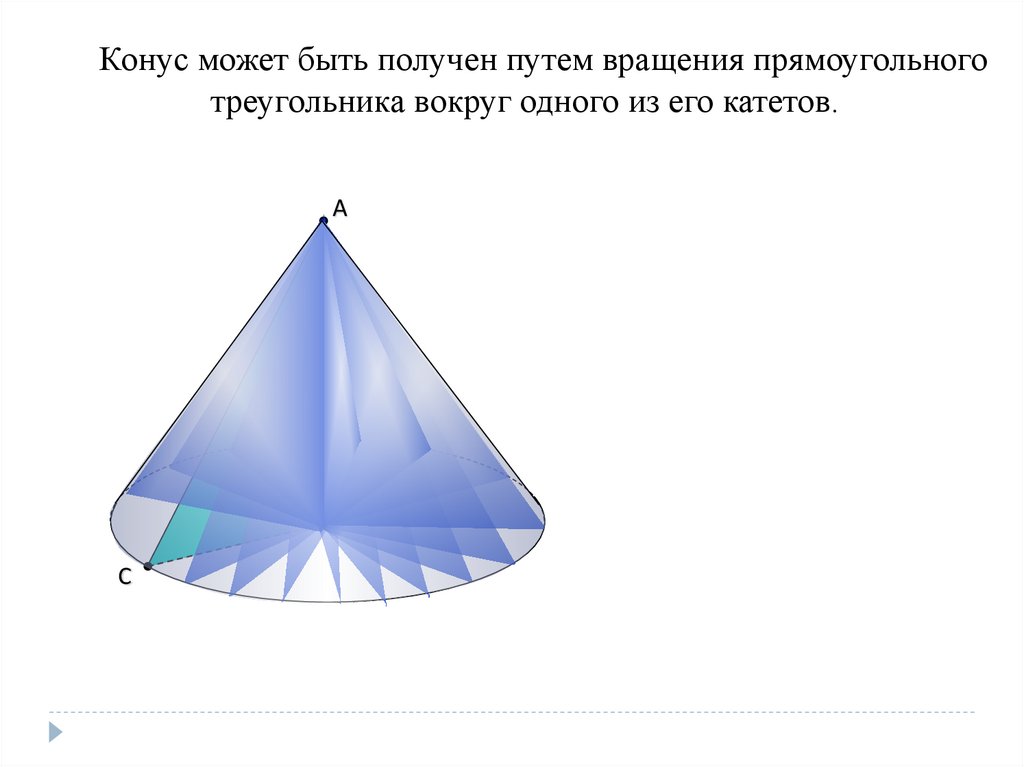
Конус может быть получен путем вращения прямоугольноготреугольника вокруг одного из его катетов.
А
В
С
5.
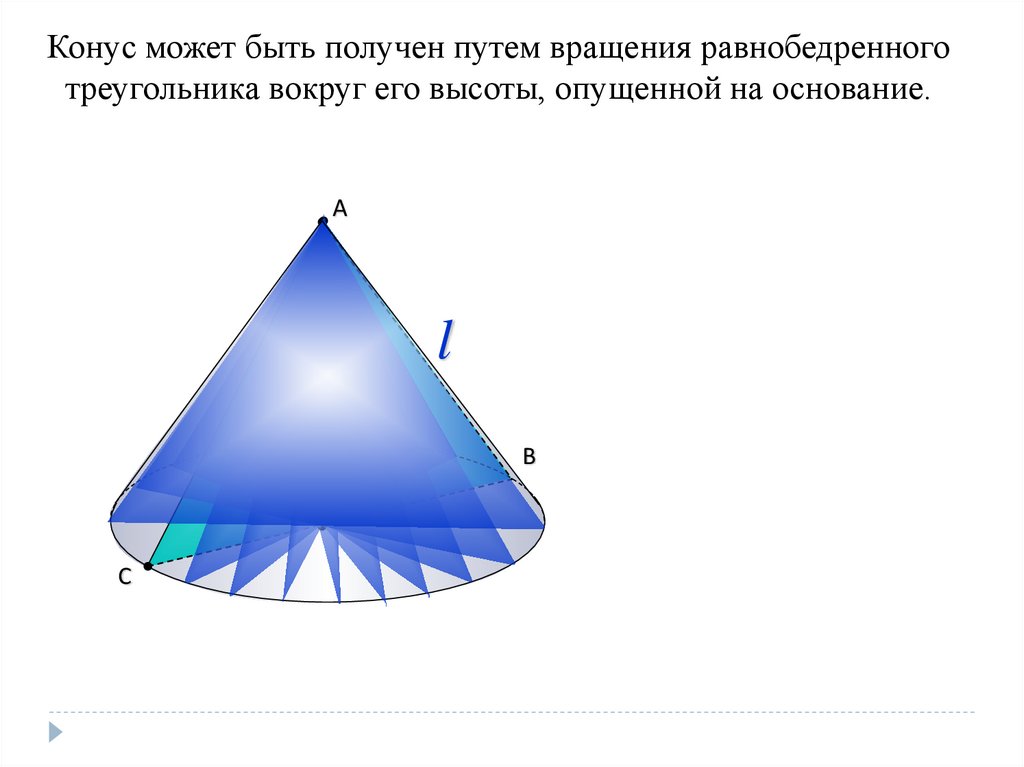
Конус может быть получен путем вращения равнобедренноготреугольника вокруг его высоты, опущенной на основание.
А
l
В
С
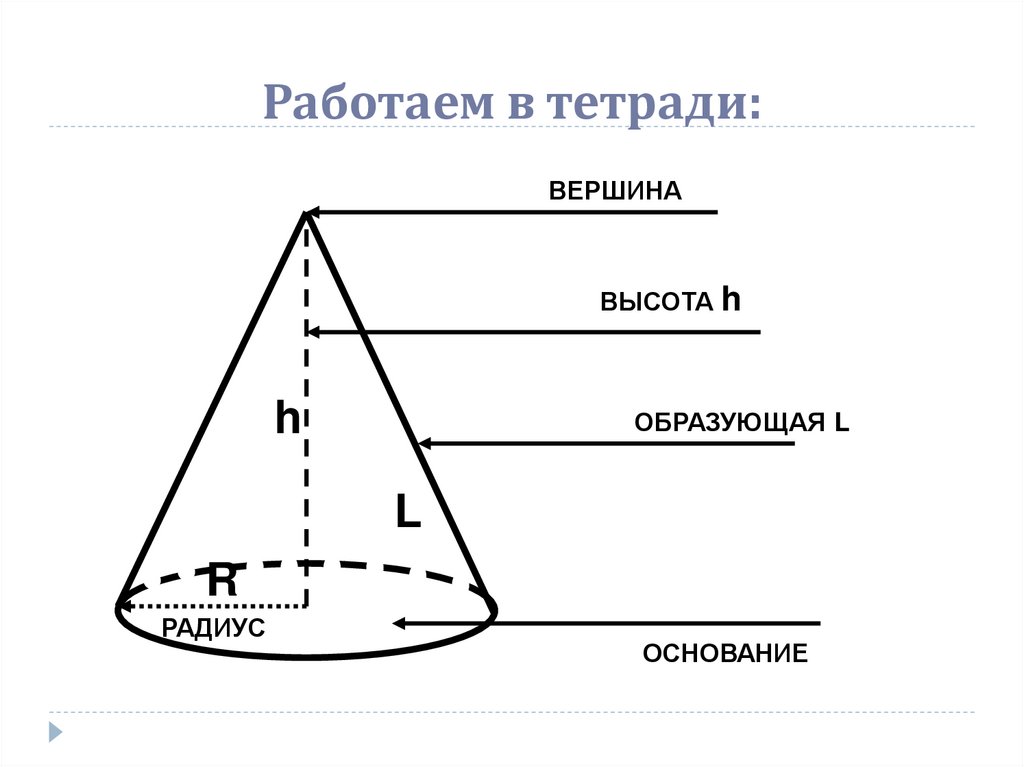
6. Работаем в тетради:
ВЕРШИНАВЫСОТА h
h
ОБРАЗУЮЩАЯ L
L
R
РАДИУС
ОСНОВАНИЕ
7.
Сечения конусаА
Осевое сечение конуса
равнобедренный остроугольный
треугольник
О
8.
Осевое сечение конусаравнобедренный прямоугольный
треугольник
А
О
9.
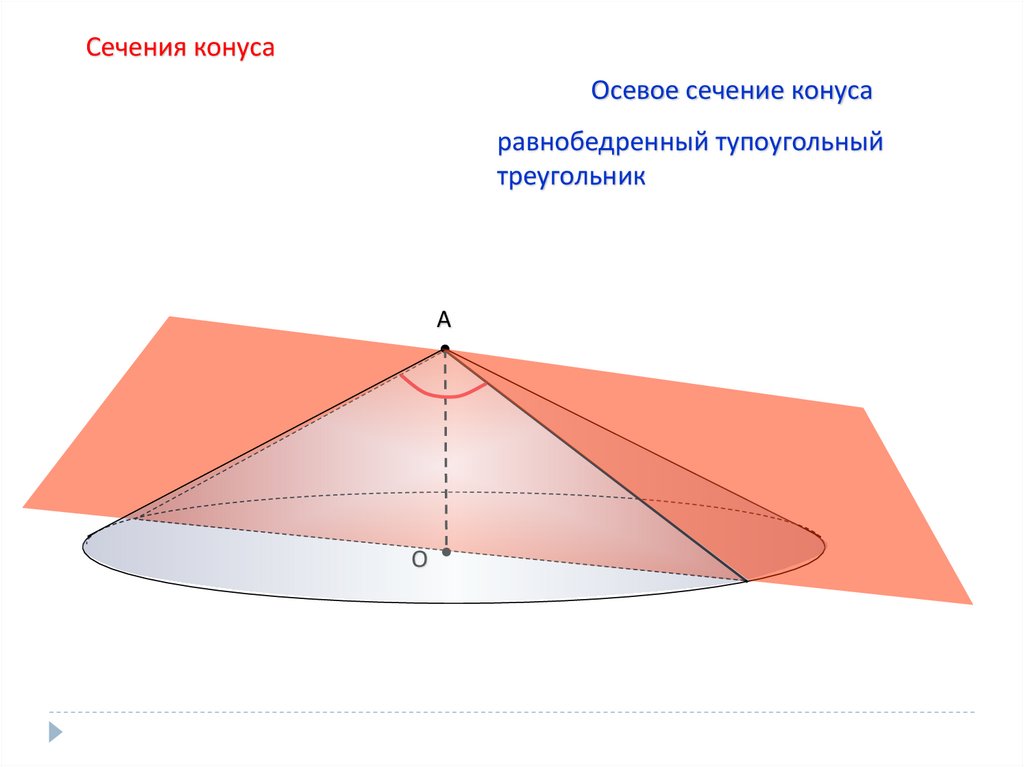
Сечения конусаОсевое сечение конуса
равнобедренный тупоугольный
треугольник
А
О
10.
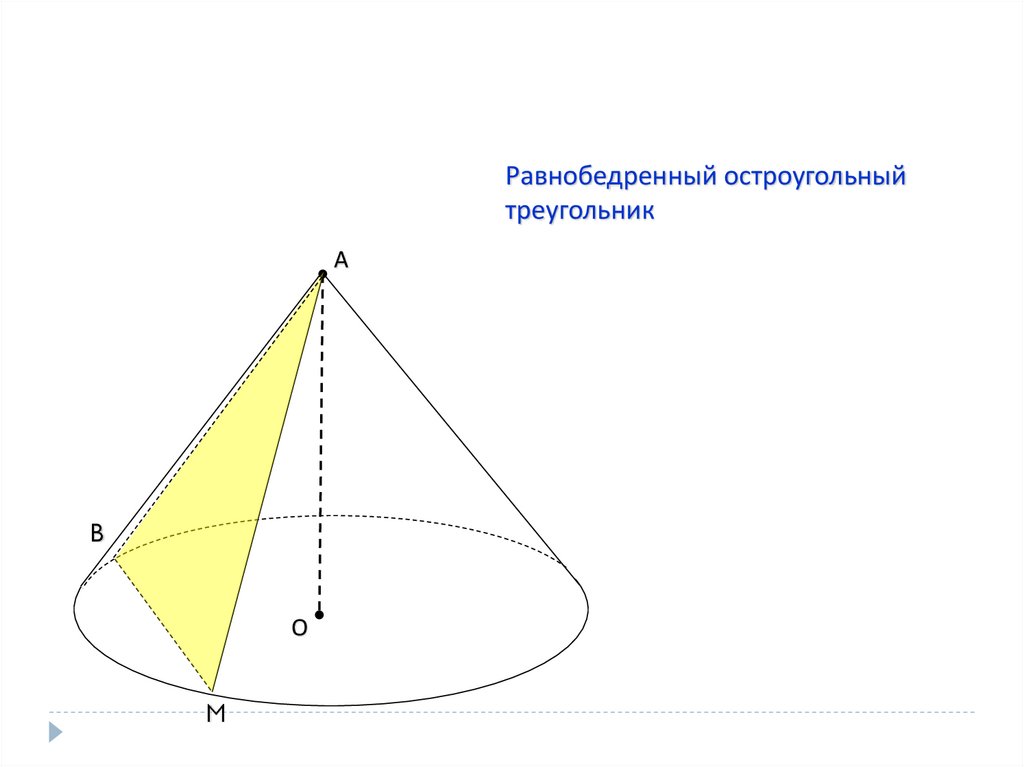
Равнобедренный остроугольныйтреугольник
А
B
О
M
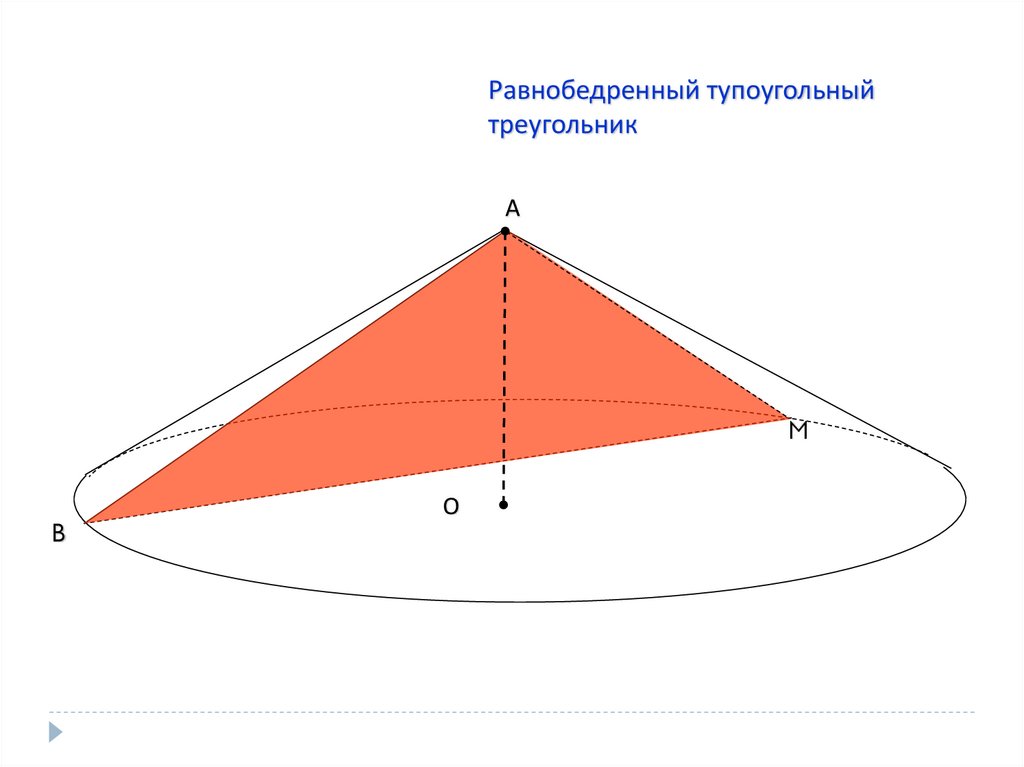
11.
Равнобедренный тупоугольныйтреугольник
А
M
B
О
12.
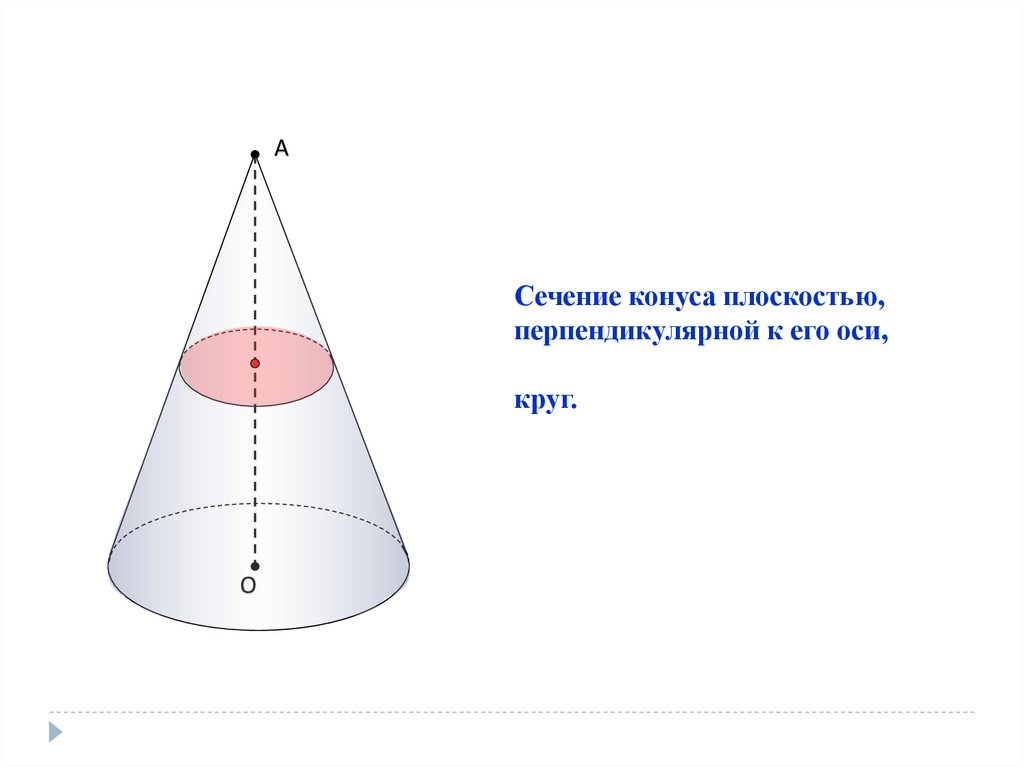
АСечение конуса плоскостью,
перпендикулярной к его оси,
круг.
О
13.
АЭллипс
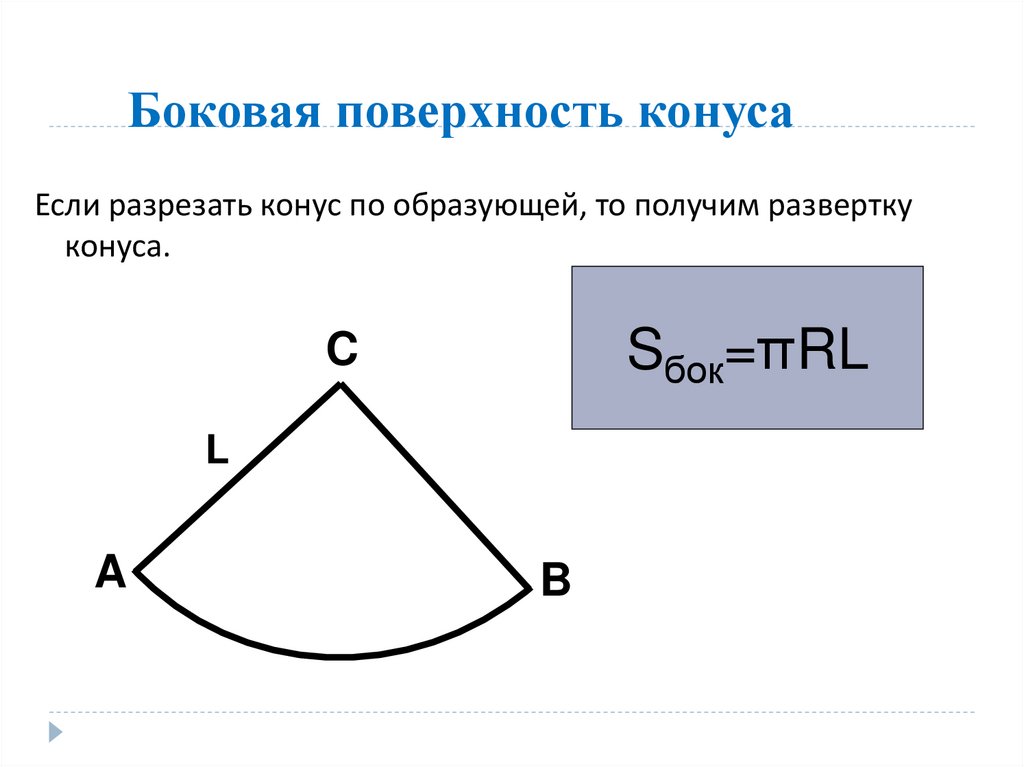
14. Боковая поверхность конуса
Если разрезать конус по образующей, то получим разверткуконуса.
Sбок=πRL
C
L
A
B
15. Формула площади полной поверхности конуса
Sп.к = Sб.к + Sосн2
Sп.к = πRl + π R
Sп.к = π R(R+l)
К
О
А
В
16.
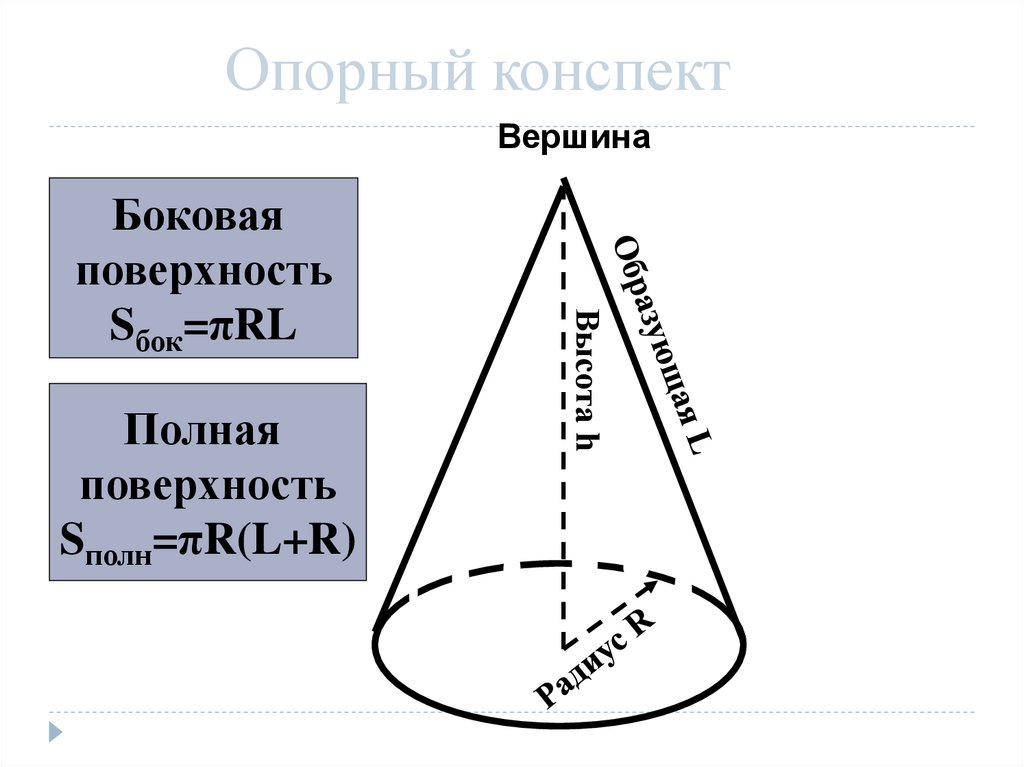
Опорный конспектВершина
Полная
поверхность
Sполн=πR(L+R)
Высота h
Боковая
поверхность
Sбок=πRL
17. ЗАДАЧА 1.
По данным чертежа (ОВ=3, КВ=5) вычислите площадьбоковой и площадь полной поверхности конуса:
К
5
А
О
3
О
В
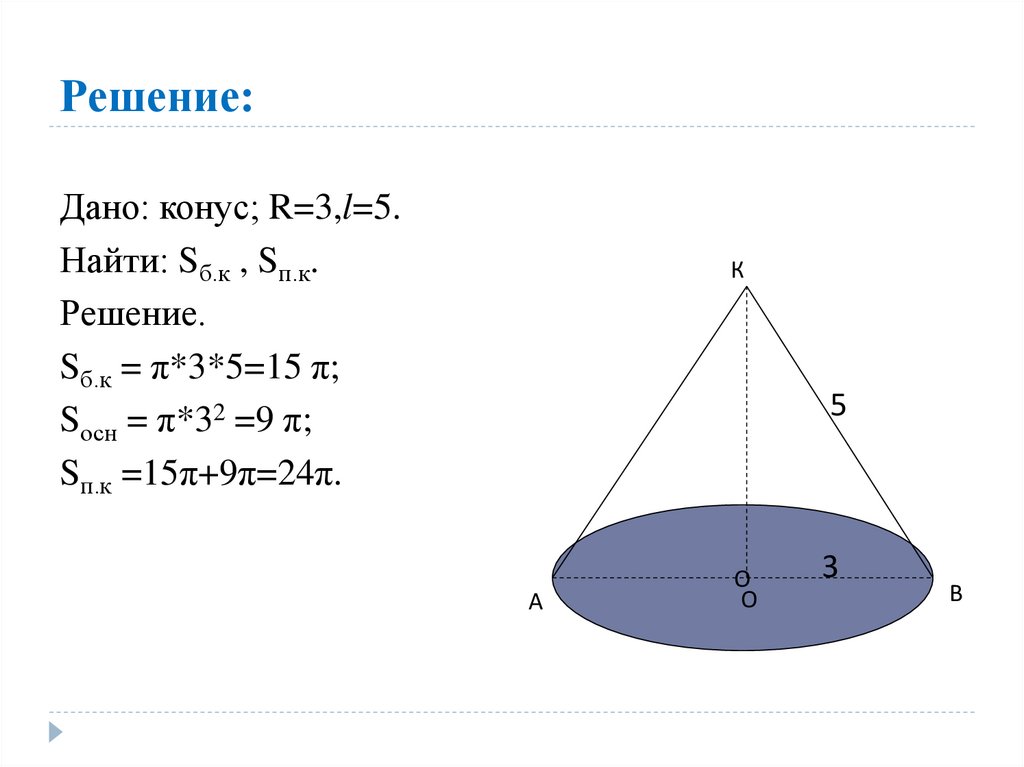
18. Решение:
Дано: конус; R=3,l=5.Найти: Sб.к , Sп.к.
Решение.
Sб.к = π*3*5=15 π;
Sосн = π*32 =9 π;
Sп.к =15π+9π=24π.
К
5
А
О
О
3
В
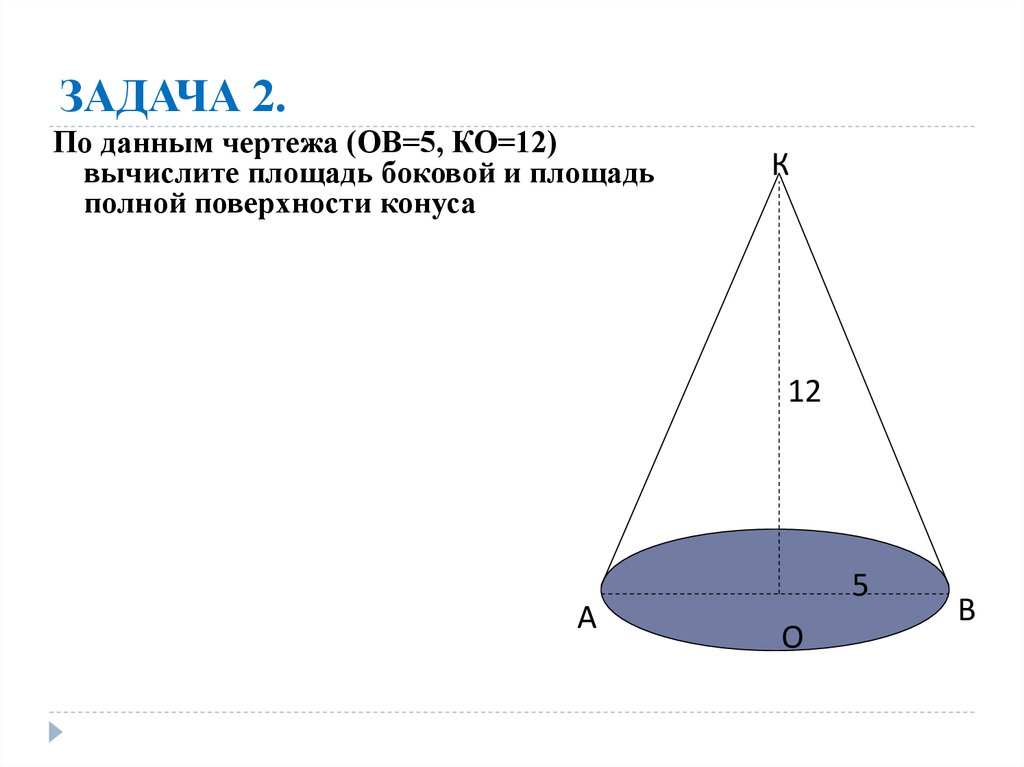
19. ЗАДАЧА 2.
По данным чертежа (ОВ=5, КО=12)вычислите площадь боковой и площадь
полной поверхности конуса
К
12
А
5
О
В
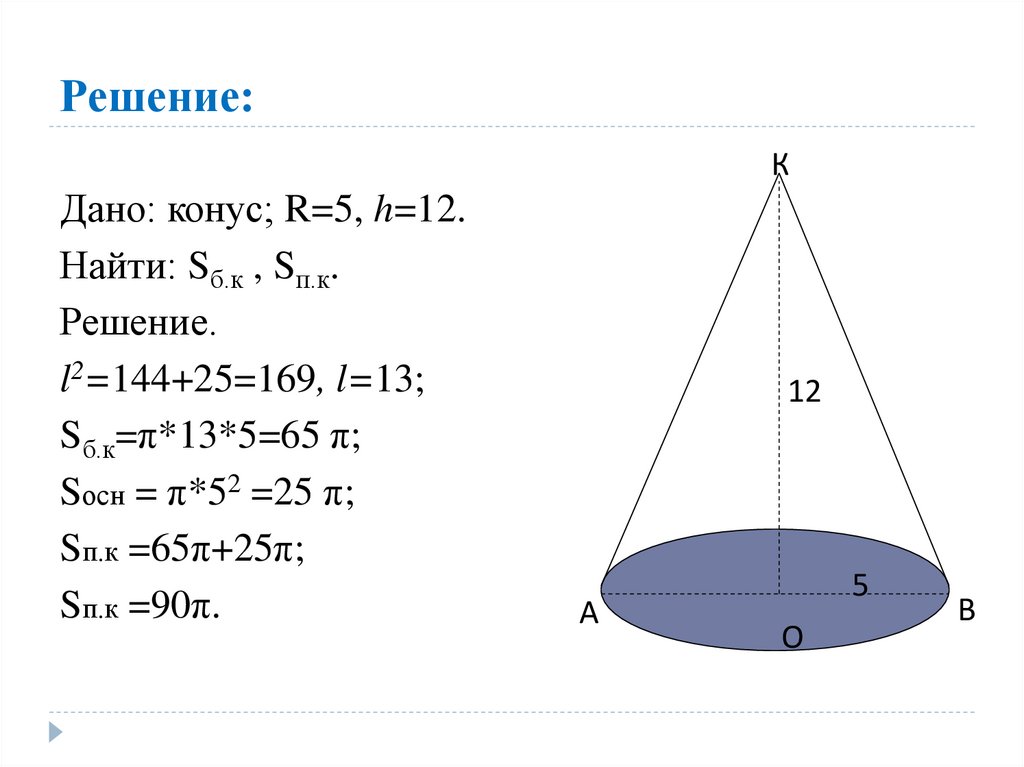
20. Решение:
КДано: конус; R=5, h=12.
Найти: Sб.к , Sп.к.
Решение.
l2=144+25=169, l=13;
Sб.к=π*13*5=65 π;
Sосн = π*52 =25 π;
Sп.к =65π+25π;
Sп.к =90π.
12
А
5
О
В
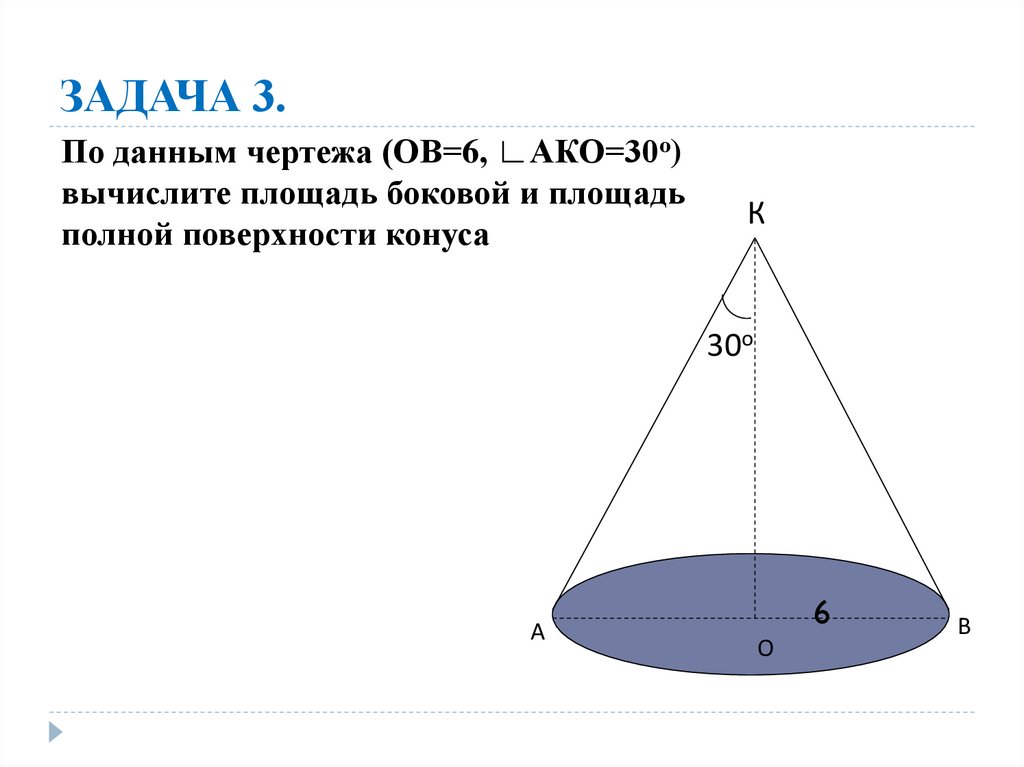
21. ЗАДАЧА 3.
По данным чертежа (ОВ=6, ∟АКО=30о)вычислите площадь боковой и площадь
полной поверхности конуса
К
30о
А
6
О
В
22. Решение:
Дано: конус;R=6,∟АКО=30о.
Найти: Sб.к , Sп.к.
Решение.
l=R/sin30о,l=6/0.5=12;
Sб.к=π*12*6=72π;
Sосн = π*62 =36π;
Sп.к =72π+36π;
Sп.к =108π.
К
30о
А
6
О
В
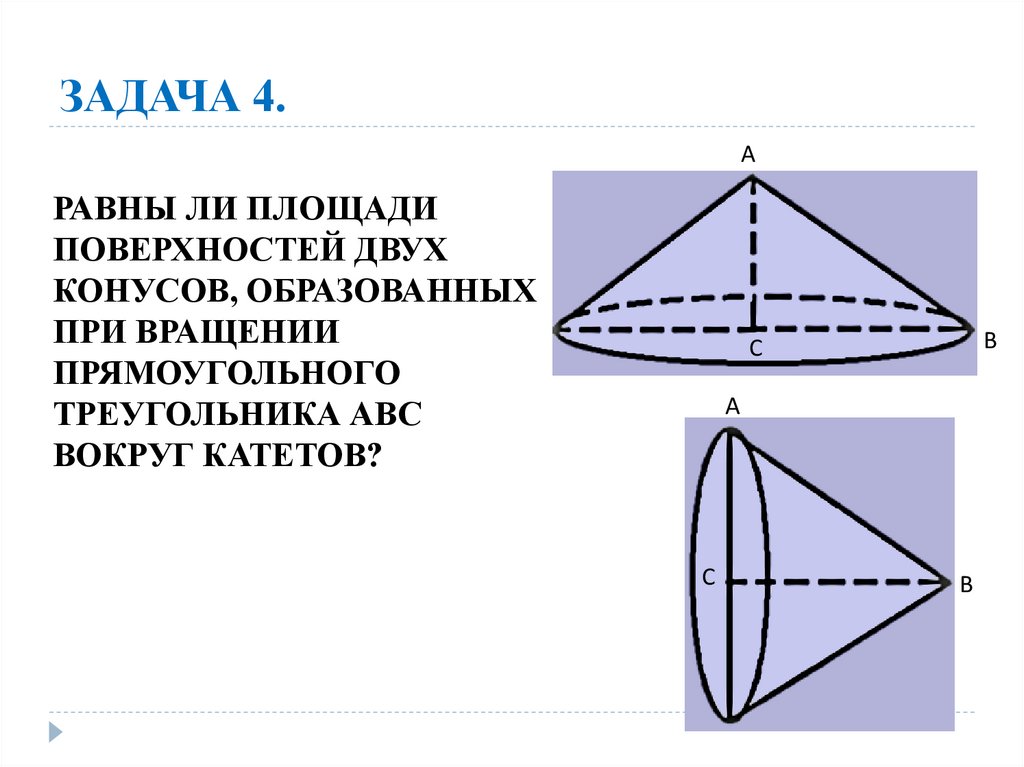
23. ЗАДАЧА 4.
АРАВНЫ ЛИ ПЛОЩАДИ
ПОВЕРХНОСТЕЙ ДВУХ
КОНУСОВ, ОБРАЗОВАННЫХ
ПРИ ВРАЩЕНИИ
ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА АВС
ВОКРУГ КАТЕТОВ?
С
С
В
А
С
С
В
24. Решение:
1. R=ВС= a ;Sп.к.1= Sб.к.1+ Sосн1=π a с+π a2 = π a (a + с).
2. R=АС= b ;
Sп.к.2= Sб.к.2+ Sосн2=π b с+π b2= π b (b + с).
Если Sп.к.1 = Sп.к.2, то
a2 +aс = b2 +bc, a2-b2+ac - bc=0, (a-b)(a+b+c)=0.
Т.к a,b,c – положительные числа (длины сторон
треугольника), то равенство верно только в случае,
если a = b.








 Математика
Математика








