Похожие презентации:
Формулы приведения для тупых углов
1.
2. Повторение материала по задачам пособия геометрии Математической вертикали
ПОВТОРЕНИЕ МАТЕРИАЛАПО ЗАДАЧАМ
ПОСОБИЯ ГЕОМЕТРИИ
МАТЕМАТИЧЕСКОЙ ВЕРТИКАЛИ
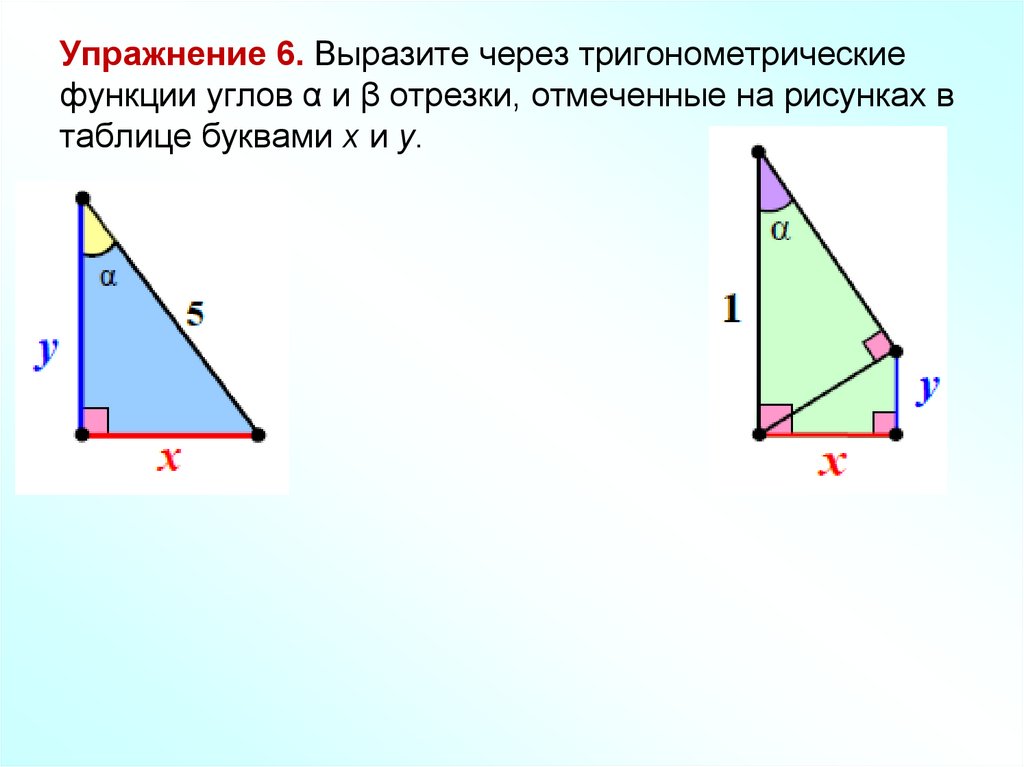
3. Упражнение 6. Выразите через тригонометрические функции углов α и β отрезки, отмеченные на рисунках в таблице буквами х и y.
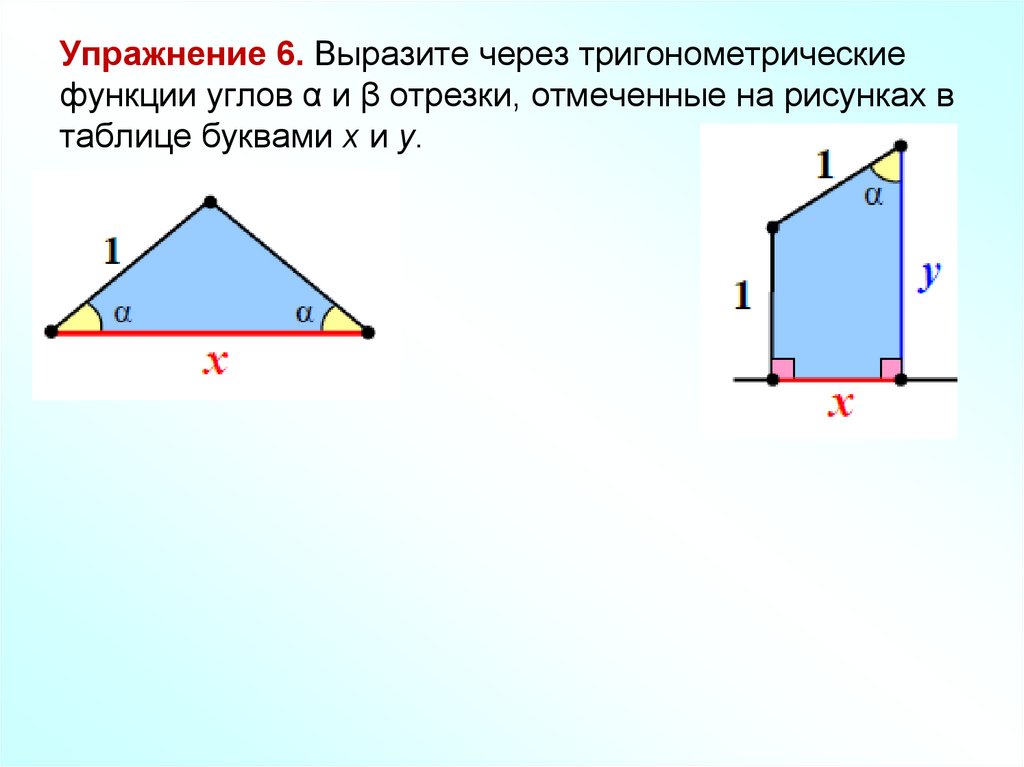
4. Упражнение 6. Выразите через тригонометрические функции углов α и β отрезки, отмеченные на рисунках в таблице буквами х и y.
5.
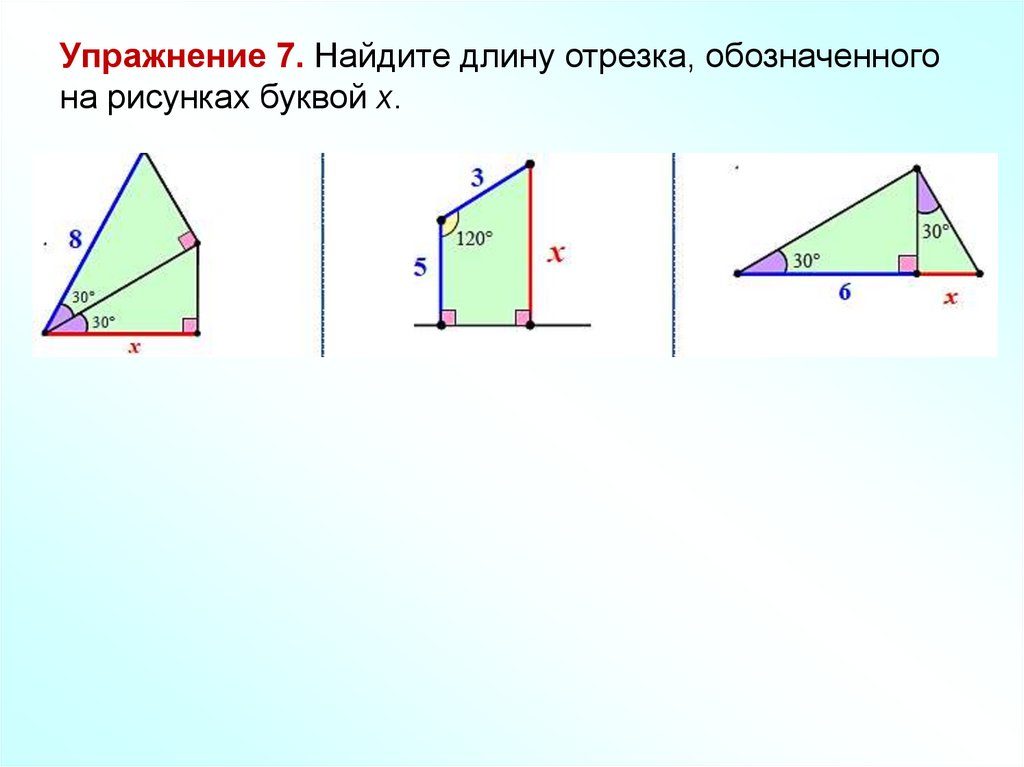
Упражнение 7. Найдите длину отрезка, обозначенногона рисунках буквой х.
6.
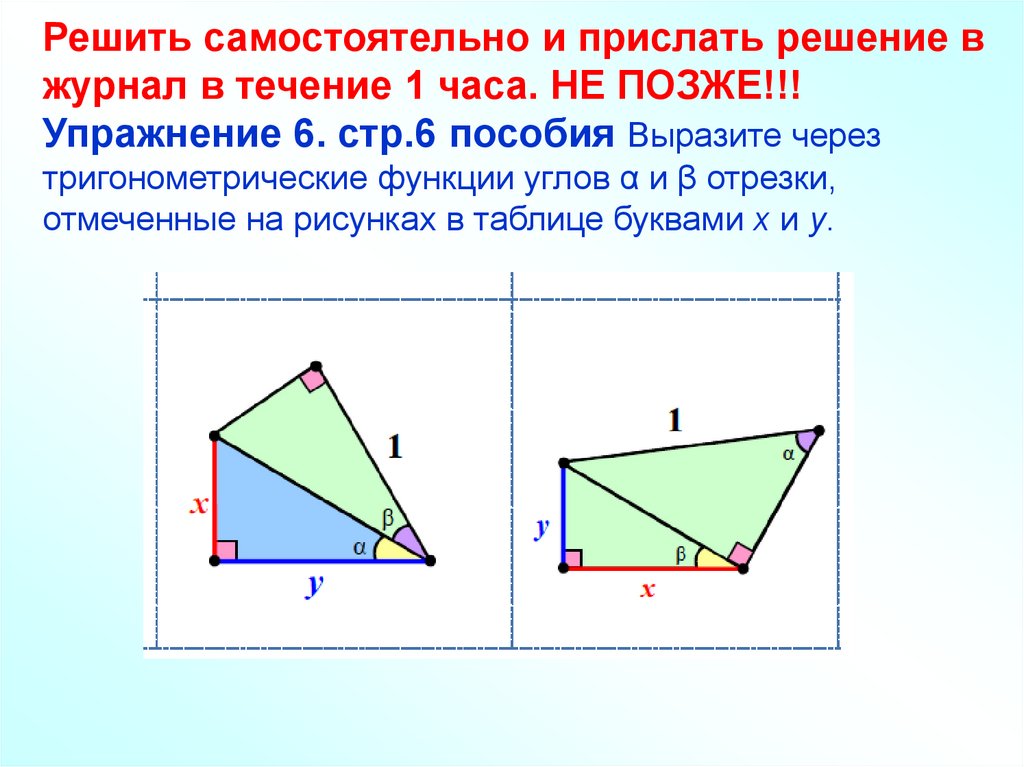
Решить самостоятельно и прислать решение вжурнал в течение 1 часа. НЕ ПОЗЖЕ!!!
Упражнение 6. стр.6 пособия Выразите через
тригонометрические функции углов α и β отрезки,
отмеченные на рисунках в таблице буквами х и y.
7.
8.
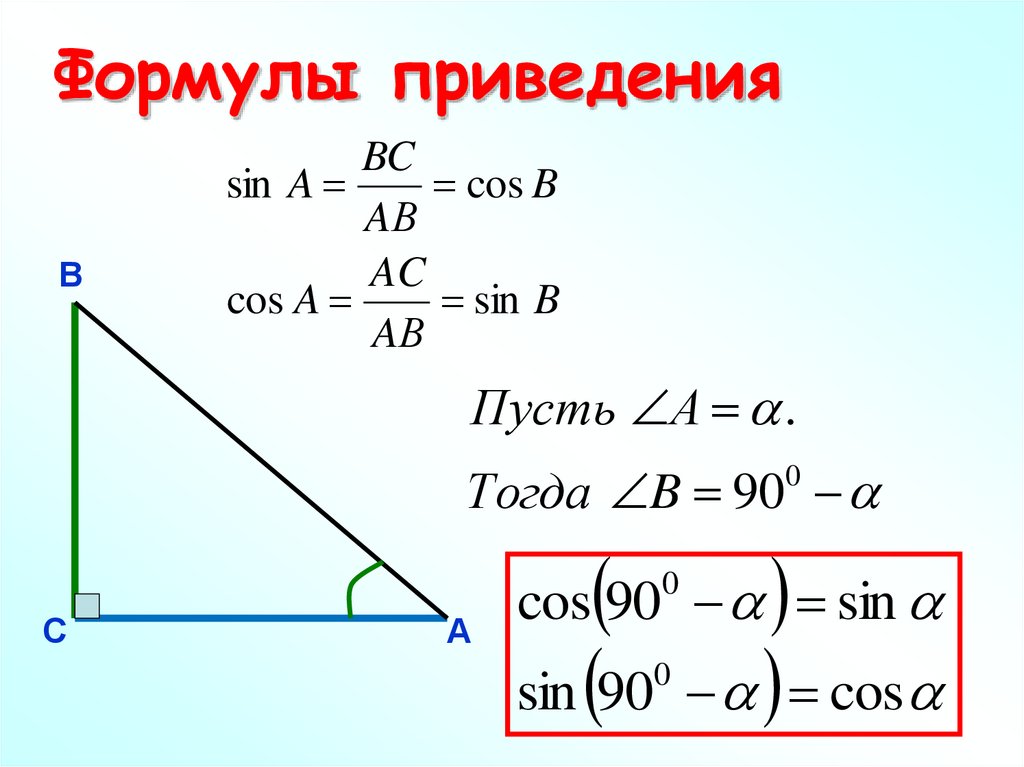
Формулы приведенияВ
BC
sin A
cos B
AВ
AC
cos A
sin B
AВ
Пусть А .
Тогда B 90
0
С
А
sin 90
cos
cos 90 sin
0
0
9.
y1800–
1800
x
O
Формулы sin( 180 )
приведения
0
cos(180 )
0
=
sin
=
cos
*
*
10.
Применение формулыприведения
sin( 180 )
0
=
sin
3
sin 120 sin( 180 60 ) sin 60
2
0
0
0
0
Синус тупого угла равен синусу смежного с ним
острого угла.
Вычислим быстро!
1
sin 150 sin 30
2
2
0
0
sin 135 sin 45
2
0
0
11.
Применение формулыприведения
cos(180 ) = cos
0
1
cos 1200 cos(180 60 ) cos 60
2
0
0
0
Косинус тупого угла равен «–» косинусу смежного с
ним острого угла.
Вычислим быстро!
3
cos 150 cos 30
2
2
0
0
cos 135 cos 45
2
0
0
12.
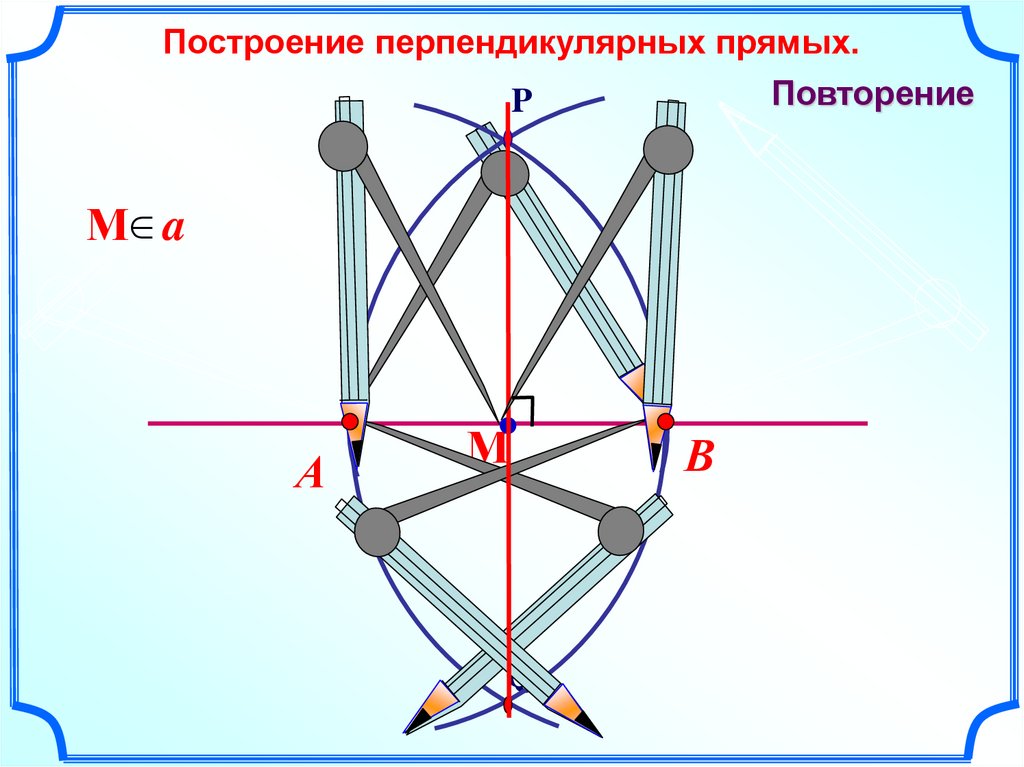
Построение перпендикулярных прямых.Повторение
P
М a
А
М
Q
В
13.
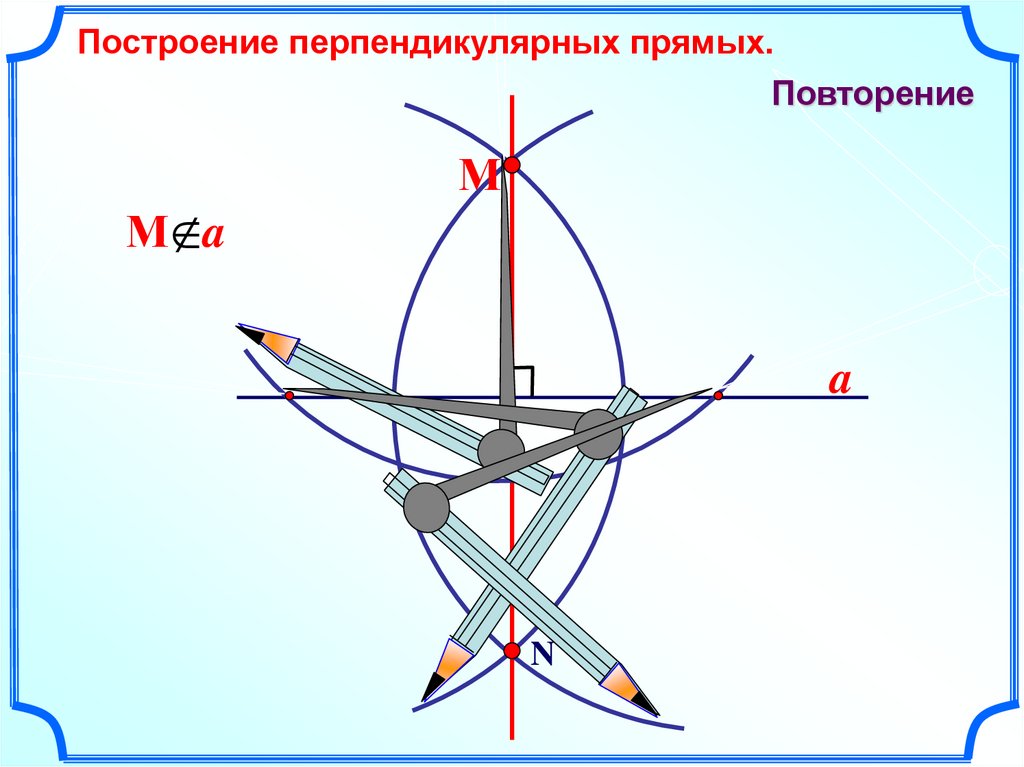
Построение перпендикулярных прямых.Повторение
М a
М
a
N
14.
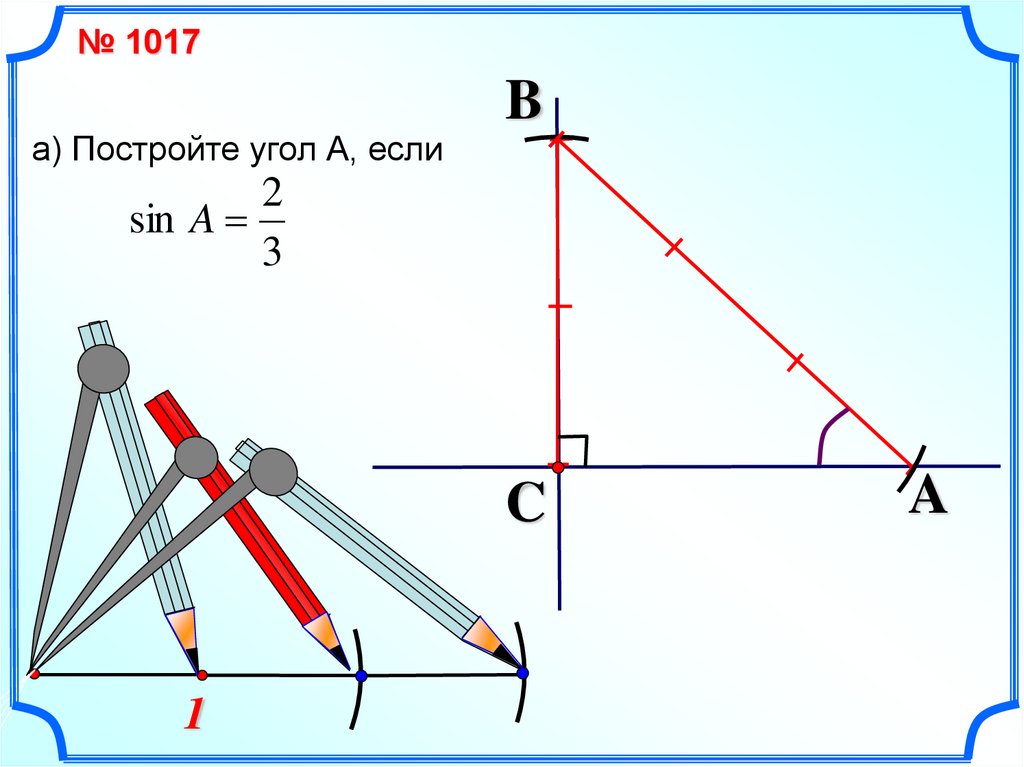
№ 1017a) Постройте угол А, если
B
2
sin A
3
C
1
A
15.
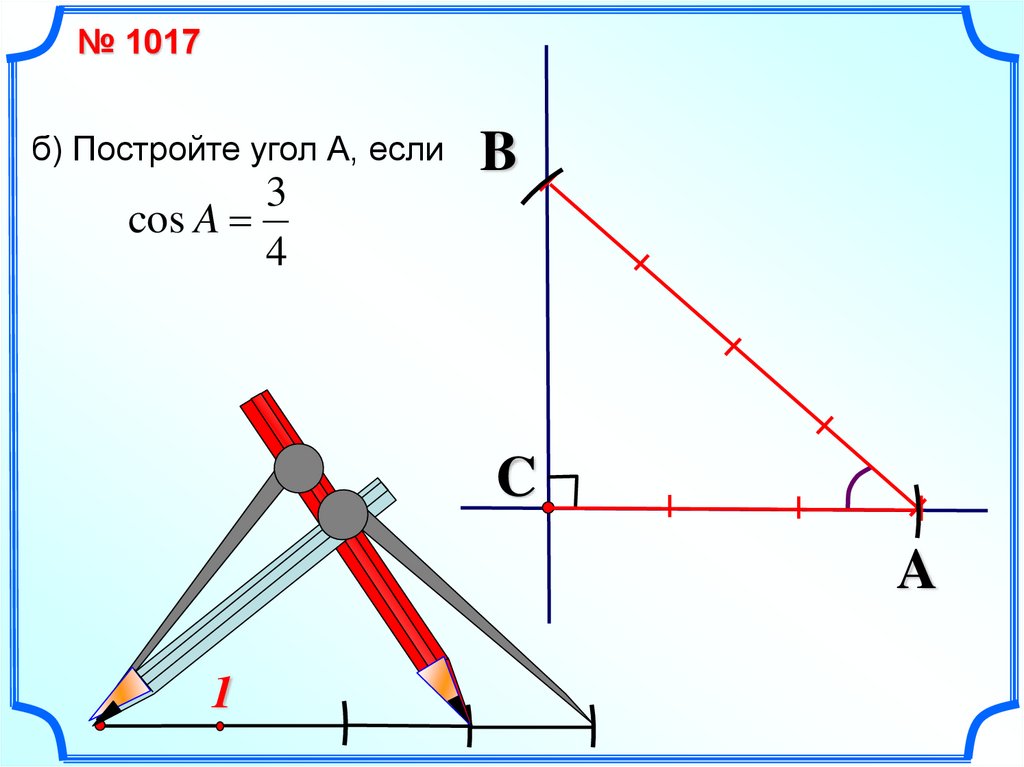
№ 1017б) Постройте угол А, если
3
cos A
4
B
C
A
1
16.
№ 1017B
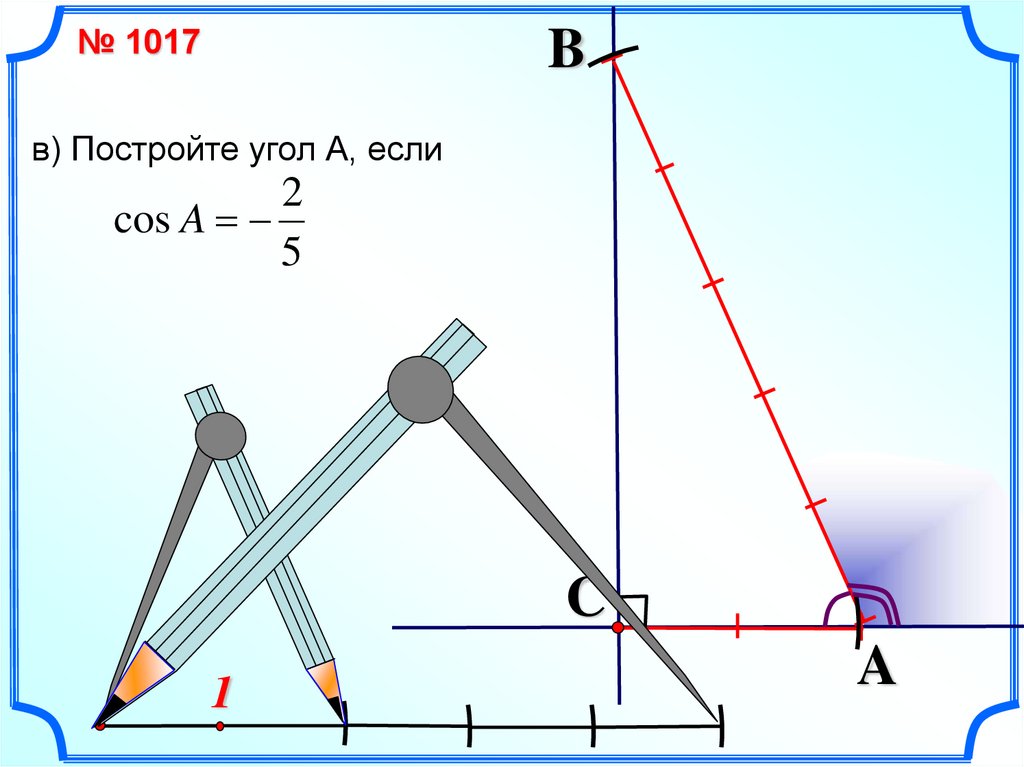
в) Постройте угол А, если
2
cos A
5
C
1
A
17.
Выражение площади треугольникачерез две его стороны и угол между
ними.
1
S ab sin
2
Площадь равностороннего
треугольника со стороной а .
S3
а
2
4
3
18.
Выражение площади четырехугольникачерез его диагонали и угол между ними.
1
S d1 d 2 sin
2
Выражение площади ромба через его
диагонали.
1
S
2
d1 d 2
Выражение площади квадрата через его
диагональ.
1 2
S d
2
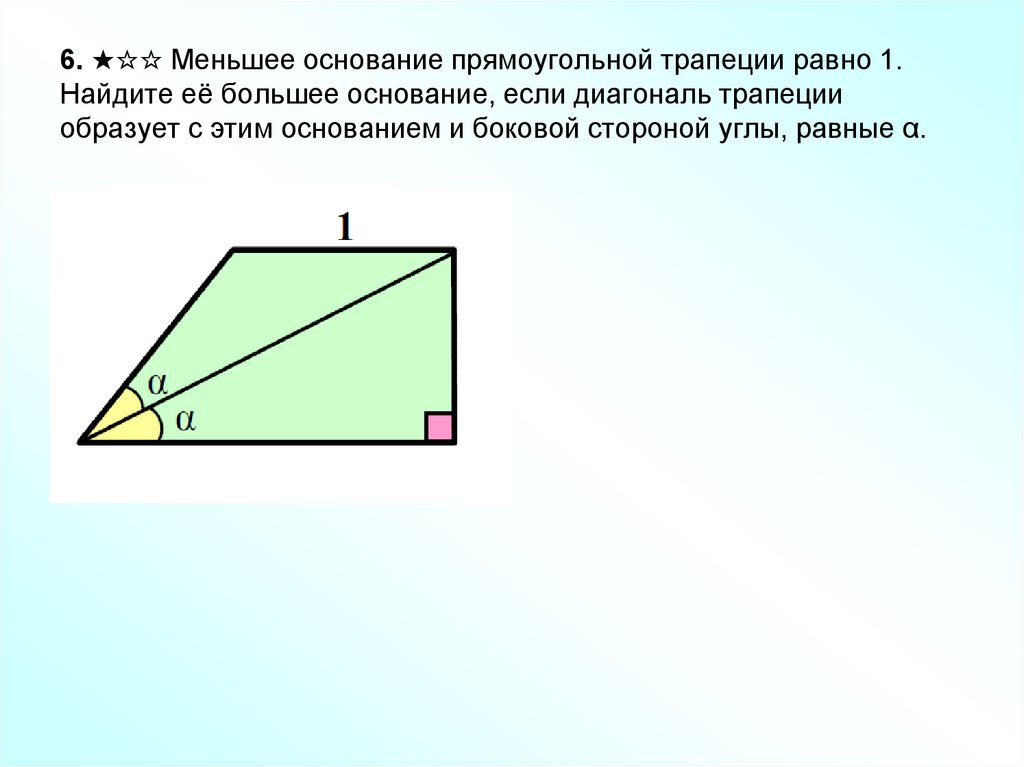
19. 6. ★☆☆ Меньшее основание прямоугольной трапеции равно 1. Найдите её большее основание, если диагональ трапеции образует с этим
основанием и боковой стороной углы, равные α.20. Задание на дом
по пособиюСтр. 14-16 и 18-20
Упр. 1-5 на стр.27









 Математика
Математика








