Формулы приведения

1. ФОРМУЛЫ ПРИВЕДЕНИЯ

2. ФОРМУЛЫ ПРИВЕДЕНИЯ

это формулы, позволяющие выражать
значения тригонометрических функций
любого угла через функции угла первой
четверти, т.е. < 90°.
-
90
0

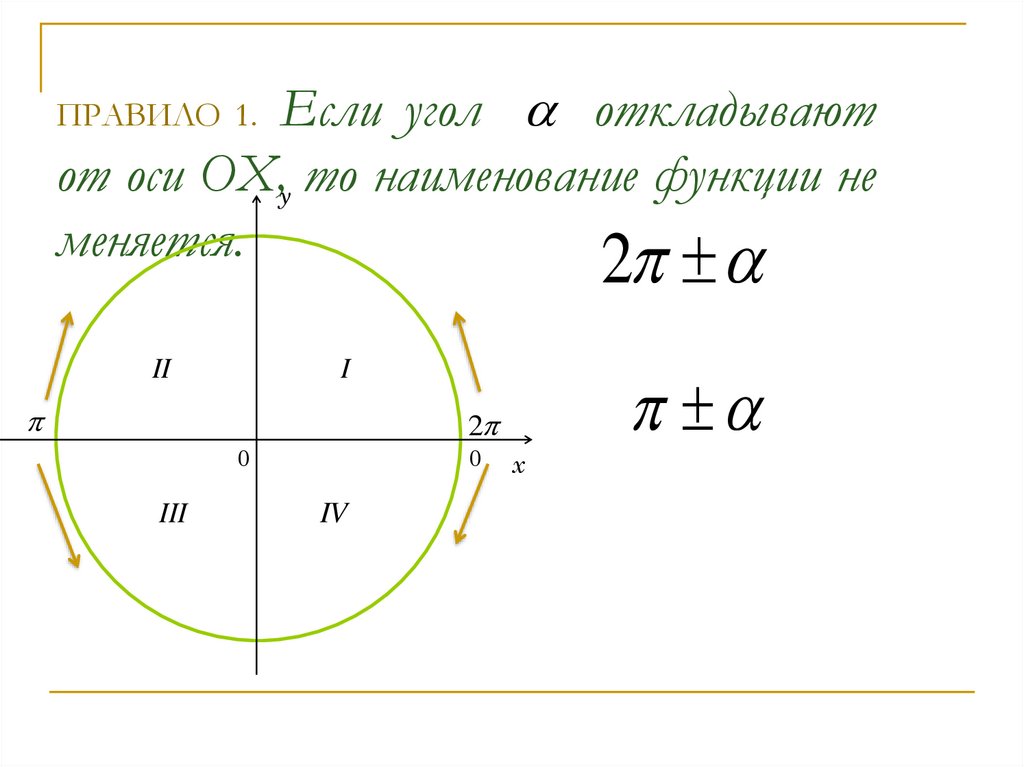
3. ПРАВИЛО 1. Если угол откладывают от оси ОX, то наименование функции не меняется.

Если угол откладывают
от оси ОX,y то наименование функции не
меняется.
2
ПРАВИЛО 1.
II
I
2
0
III
0
IV
x

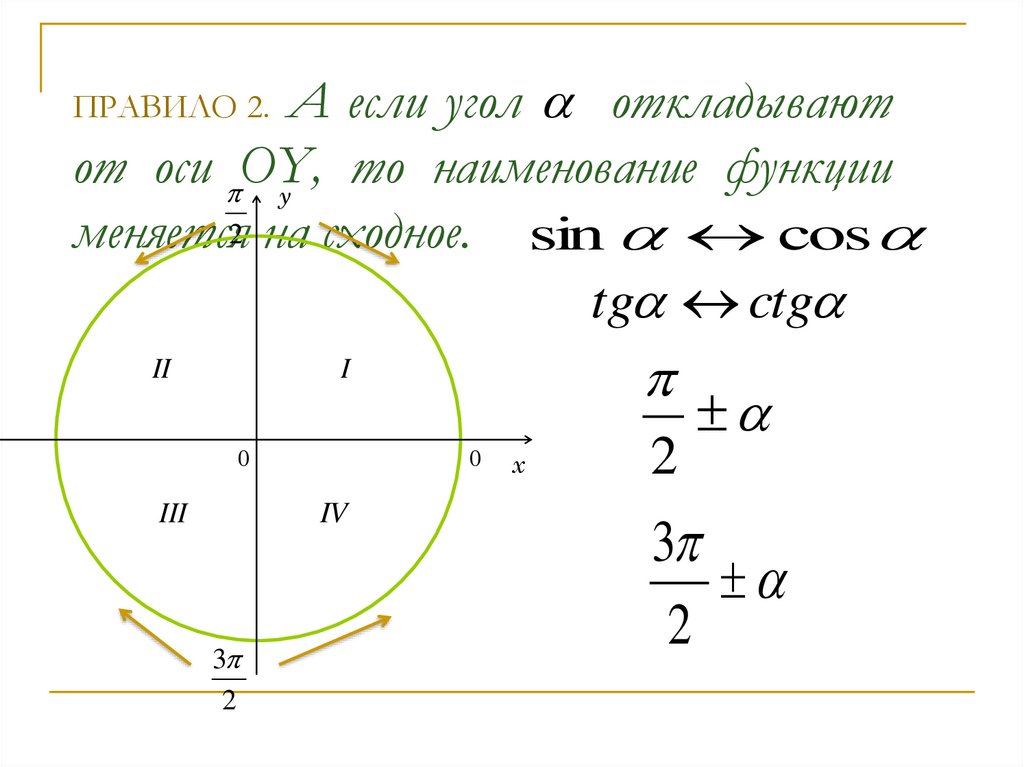
4. ПРАВИЛО 2. А если угол откладывают от оси ОY, то наименование функции меняется на сходное.

А если угол откладывают
от оси ОY,
то
наименование
функции
y
меняется2 на сходное. sin cos
tg ctg
ПРАВИЛО 2.
II
I
0
0
IV
III
3
2
x
2
3
2

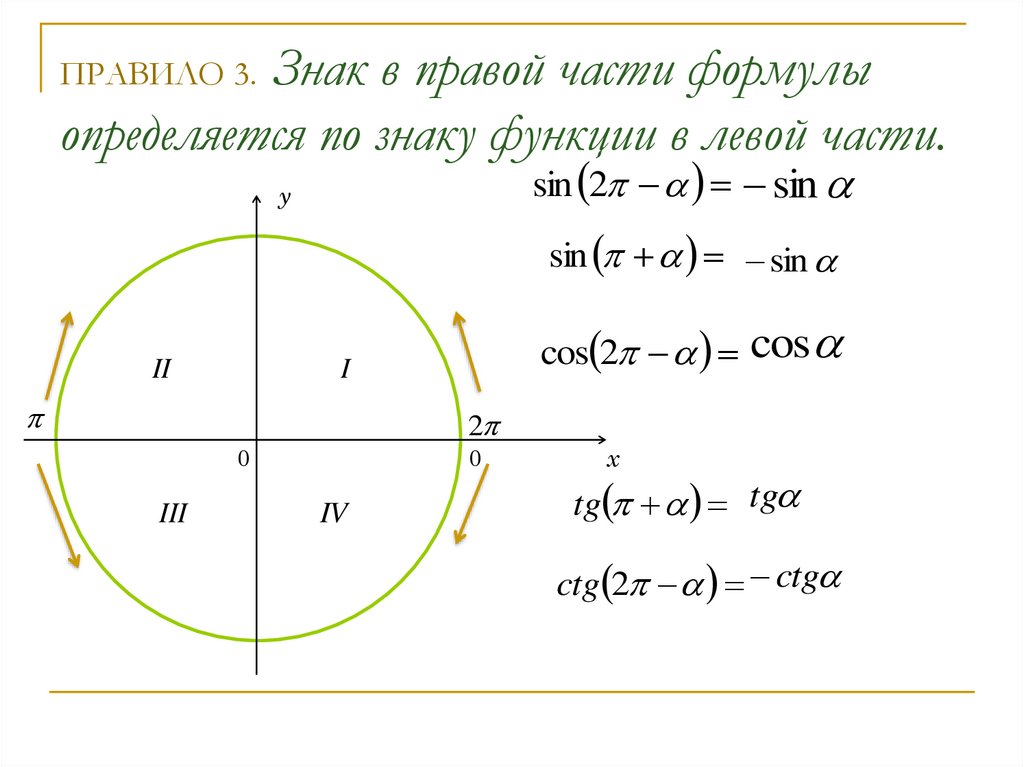
5. ПРАВИЛО 3. Знак в правой части формулы определяется по знаку функции в левой части.

Знак в правой части формулы
определяется по знаку функции в левой части.
ПРАВИЛО 3.
sin 2 sin
y
sin sin
II
cos 2
I
2
0
III
0
IV
cos
x
tg tg
ctg 2 ctg

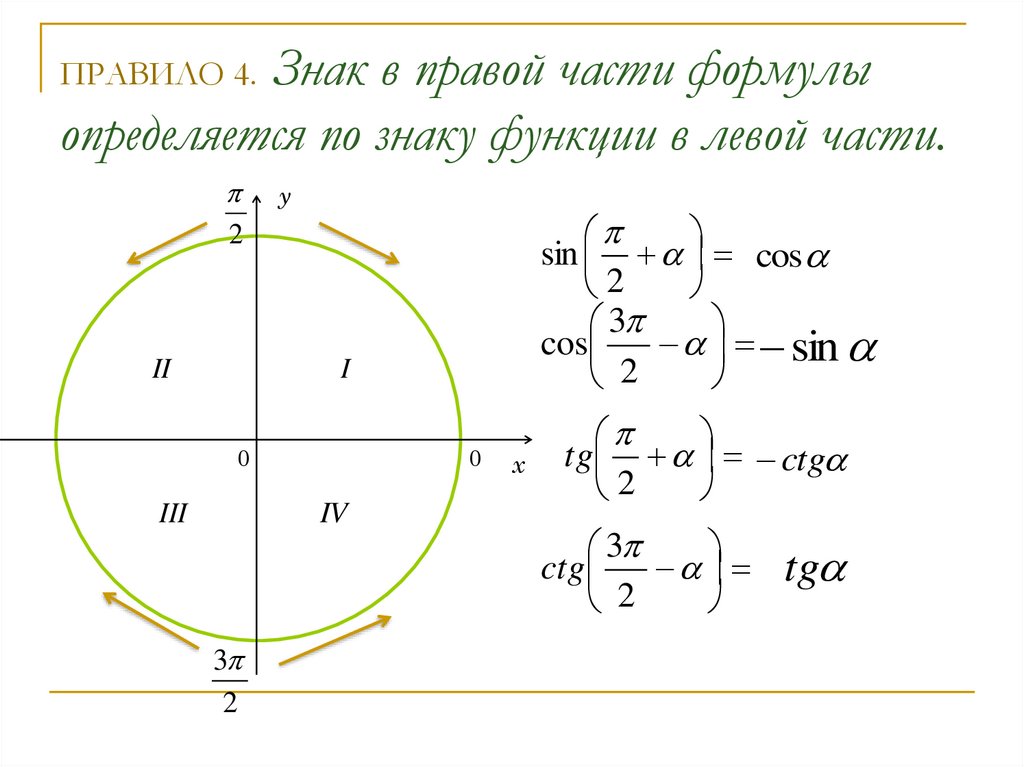
6. ПРАВИЛО 4. Знак в правой части формулы определяется по знаку функции в левой части.

Знак в правой части формулы
определяется по знаку функции в левой части.
ПРАВИЛО 4.
2
II
y
sin cos
2
3
cos
sin
2
I
0
0
IV
III
3
2
x
tg ctg
2
3
ctg
2
tg

7. Запишите формулы приведения

sin 90 0
tg 270
cos
ctg
cos 180 0 cos
0
sin 270 0 cos
sin
cos 90 0 sin
sin 360 0

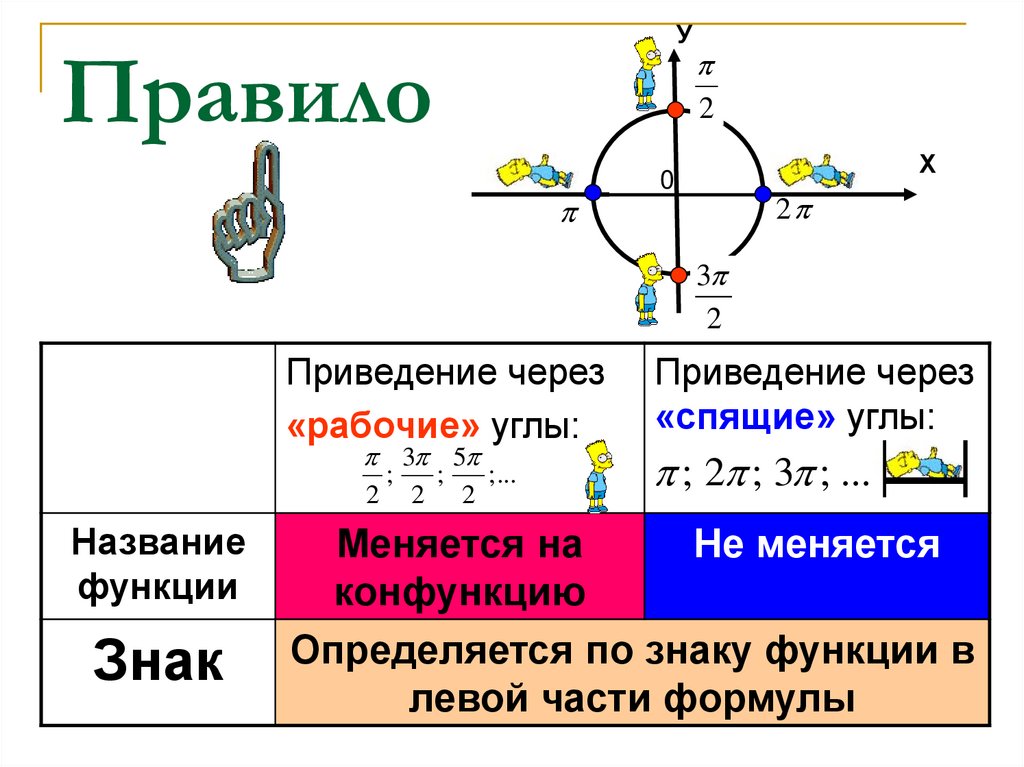
8. Правило

У
Правило
2
Х
0
2
3
2
Приведение через
«рабочие» углы:
3 5
2
Название
функции
Знак
;
2
;
2
; ...
Приведение через
«спящие» углы:
; 2 ; 3 ; ...
Меняется на
Не меняется
конфункцию
Определяется по знаку функции в
левой части формулы

9. ФОРМУЛЫ ПРИВЕДЕНИЯ

α
sinα
cosα
tgα
ctgα
2 -α
2 +α
cosα
sinα
ctgα
tgα
cosα sinα - sinα - cosα - cosα - sinα
- sinα - cosα - cosα - sinα sinα cosα
- ctgα - tgα
tgα
ctgα - ctgα - tgα
- tgα - ctgα ctgα
tgα
- tgα - ctgα
π-α
3
3
π + α 2 -α 2 +α 2π - α 2π + α
sinα
cosα
tgα
ctgα

10. Пример 1.Выразите тригонометрические функции через угол меньше 45°.

sin 168 sin 180 12 sin 12
cos123 cos 90 33 sin 33
tg174
tg 180 6 tg6
tg 263 tg 270 7 ctg 7
ctg 380 ctg 360 20 ctg 20
cos 969 cos 270 31 sin 31

11. Пример 2. Упростите выражение.

3 cos 3 cos 360 cos 90 sin 90
3 cos 3 cos sin sin 2 sin

12. Пример 3. Упростите выражение.

tg132 ctg 228 cos115 cos 245
ctg197 ctg 253 tg155 tg 295
tg 90 42 ctg 270 42 cos 90 25 cos 270 25
ctg 180 17 ctg 270 17 tg 180 25 tg 270 25
ctg 42 tg 42 sin 25 sin 25
ctg17 tg17 tg 25 ctg 25
1 sin 2 25 1
cos 2 25
2
2

13. Свойства и график функции y = sinx

14. Тригонометрические функции Функция y = sin x

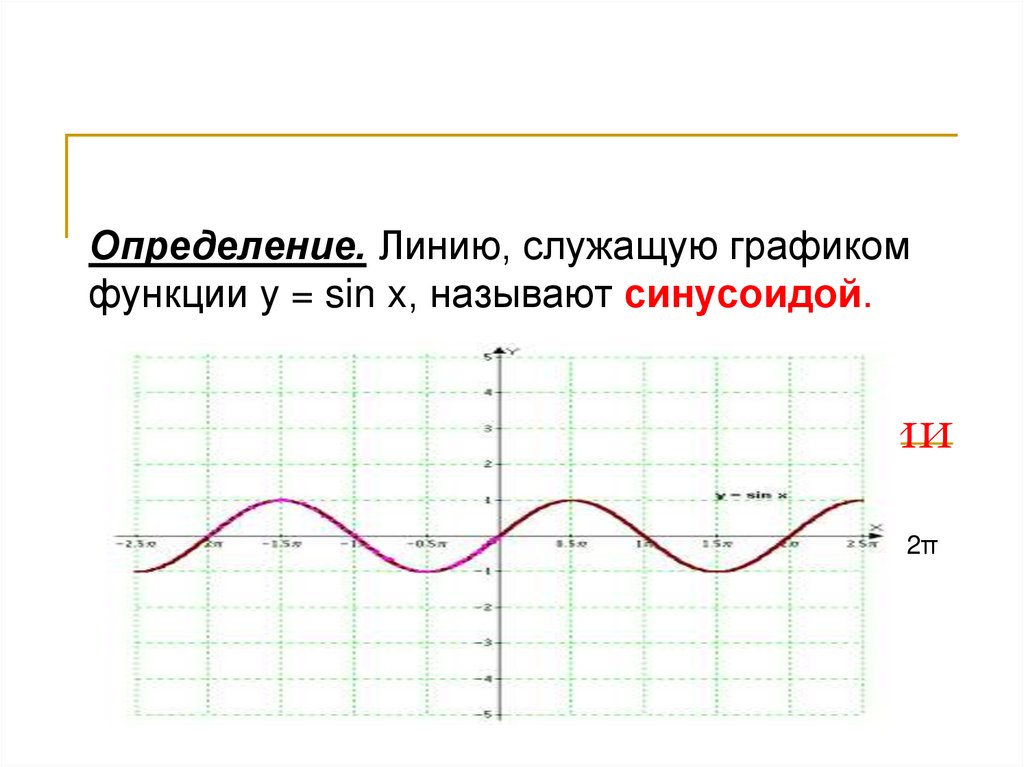
Определение. Линию, служащую графиком
функции y = sin x, называют синусоидой.
Тригонометрические функции
Функция y = sin x
π
2π

15.

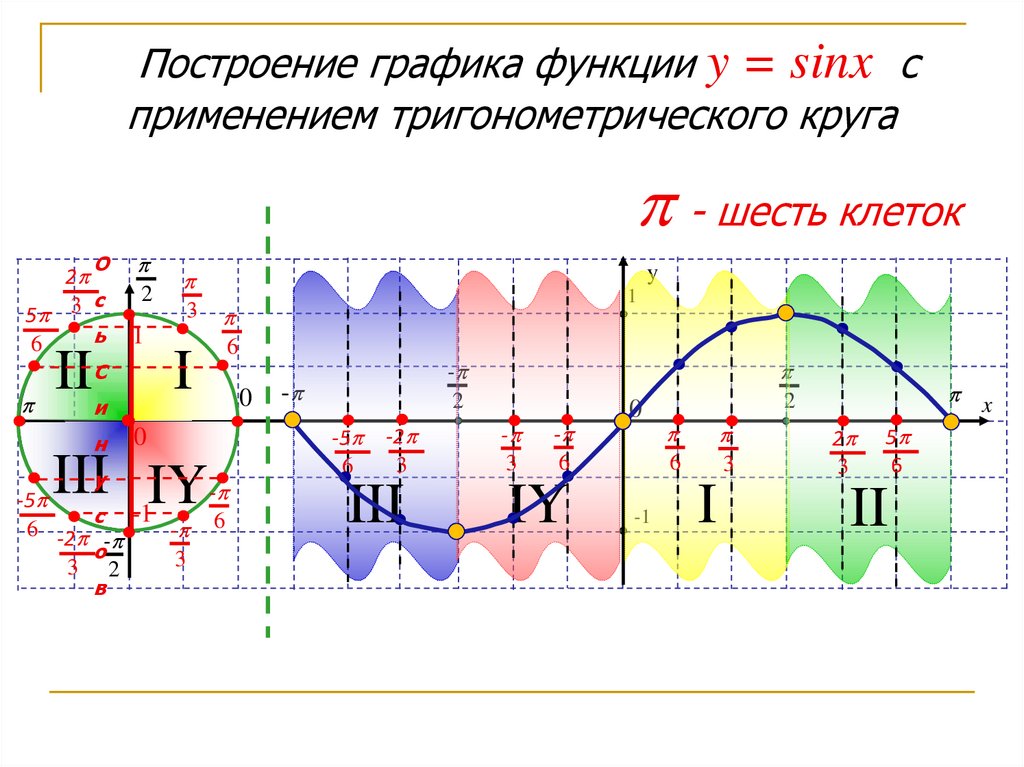
Построение графика функции y = sinx с
применением тригонометрического круга
- шесть клеток
О
2
с
5 3
ь
6
II
2
I
и
н
III
у
3
1
С
y
6
0
IY
-
-5
с -1
6
6 -2
-
о
3
3 2
в
1
0
-
2
-
-5
6
-2
3
III
-
3
-
6
IY
0
-1
x
2
6
3
I
2
3
5
6
II

16. Свойства функции y = sin x.

Свойство 1. D(y) = (-∞;+∞).
Свойство 2. y = sin x – нечетная функция.
Свойство 3. Функция y = sin x убывает на отрезке [-π/2+2πk; π/2
+ 2πk] и возрастает на отрезке [π/2 + 2πk; 3π/2 + 2πk ], где k є Z.
Свойство 4. Функция ограничена и сверху и снизу (-1 ≤ sin t ≤ 1).
Свойство 5. yнаим = -1; yнаиб = 1.
Свойство 6. Функция y = sin x периодическая, ее основной
Свойства функции y = sin x.
период равен 2π.
Свойство 7. y = sin x – непрерывная функция.
Свойство 8. E(y) = [-1;1].
Свойство 9. Функция выпукла вверх на отрезке [0 + 2πk; π +
2πk],
выпукла вниз на отрезке [π + 2πk; 2π + 2πk], где k є Z.

17.

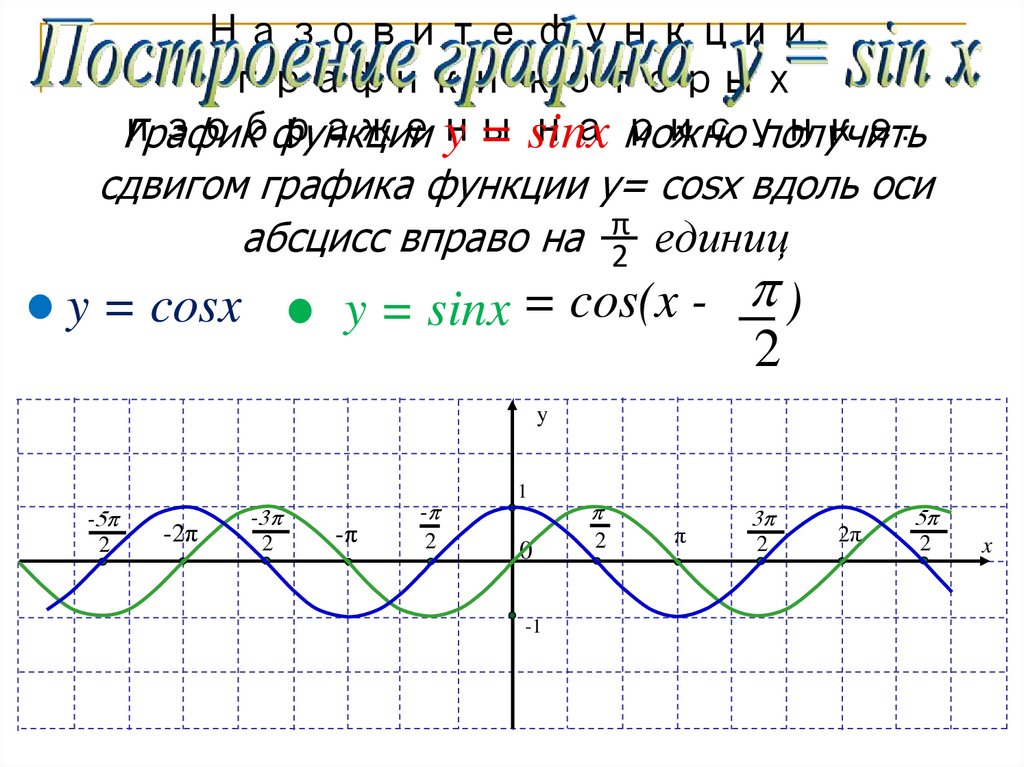
Назовите функции,
графики которых
изображены
на рисунке.
График функции y = sinx
можно получить
сдвигом графика функции у= cosх вдоль оси
абсцисс вправо на π2 единиц
=
cos(x
)
y = sinx
y = cosx
2
y
-5
2
-2π
-3
2
-π
-
2
1
0
-1
2
π
3
2
2π
5
2
x

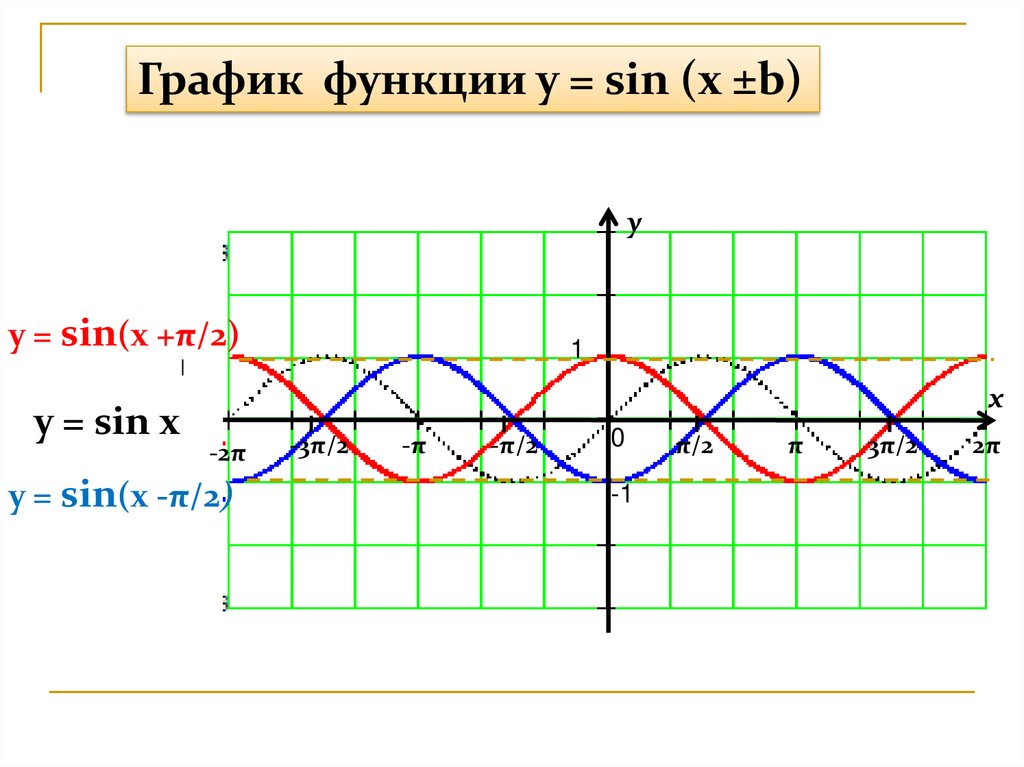
18.

График функции y = sin (x ±b)
y
y = sin(x +π/2)
y = sin x
1
x
-2π
y = sin(x -π/2)
-3π/2
-π
-π/2
0
-1
π/2
π
3π/2
2π

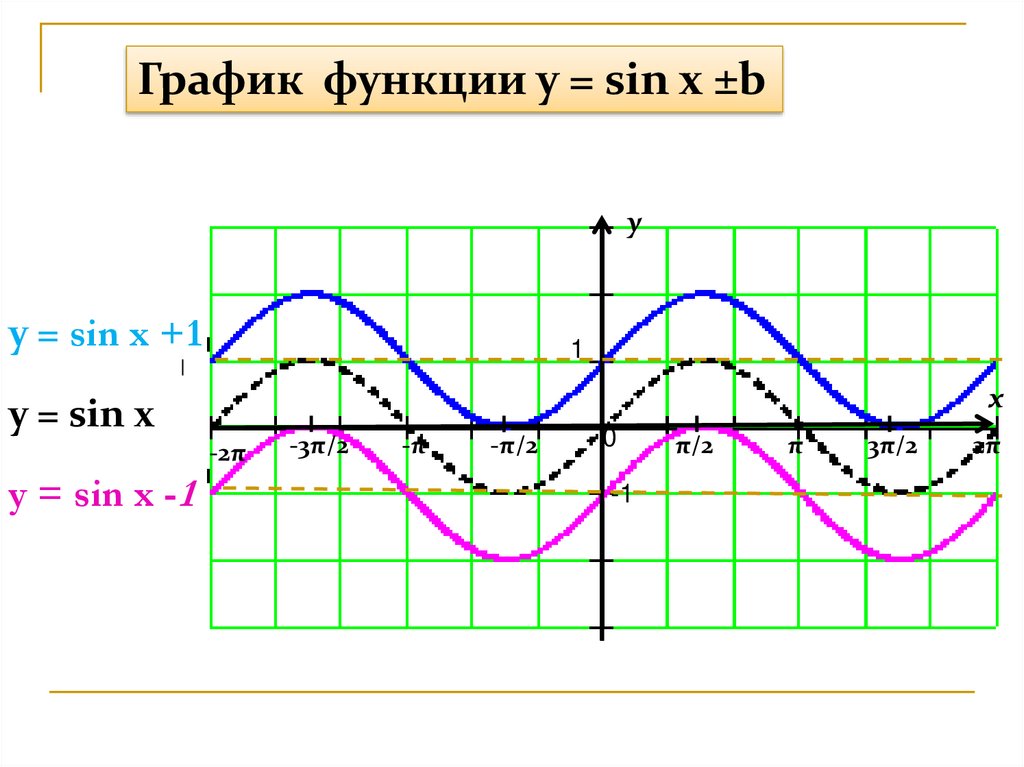
19.

График функции y = sin x ±b
y
y = sin x +1
1
x
y = sin x
-2π
y = sin x -1
-3π/2
-π
-π/2
0
-1
π/2
π
3π/2
2π

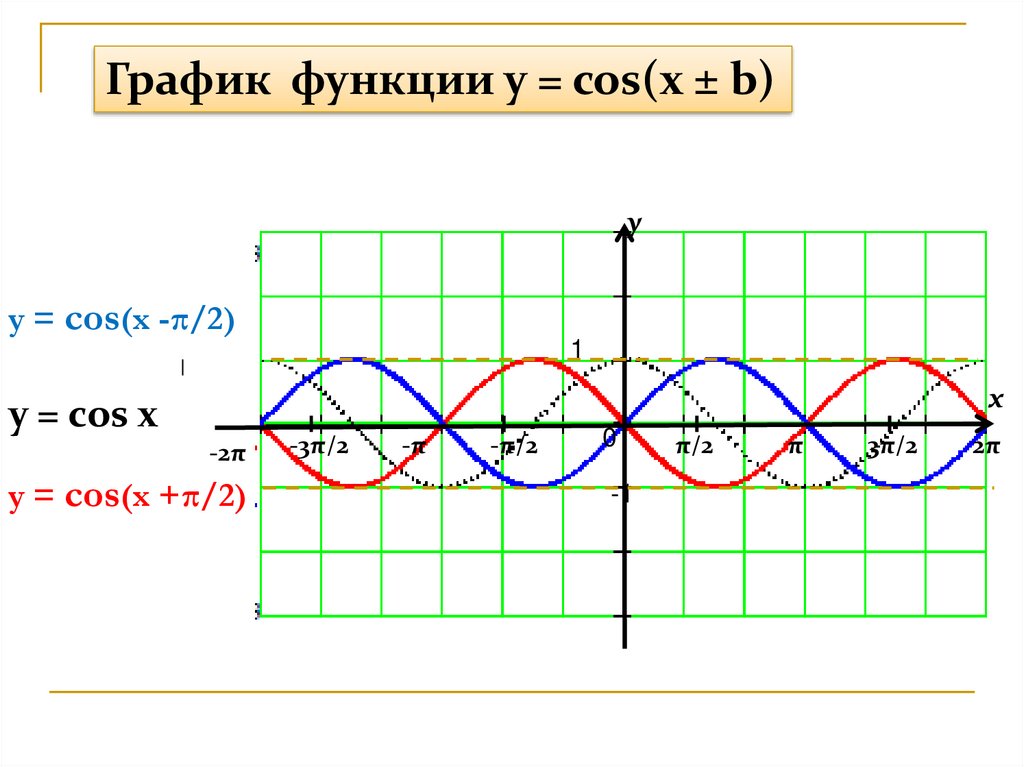
20.

График функции y = cos(x ± b)
y
y = cos(x -π/2)
1
x
y = cos x
-2π
y = cos(x +π/2)
-3π/2
-π
-π/2
0
-1
π/2
π
3π/2
2π

21. Преобразование графиков тригонометрических функций

График функции у = f (x+в) получается из графика функции
у = f(x) параллельным переносом на (-в) единиц вдоль оси
абсцисс
График функции у = f (x)+а получается из графика функции
у = f(x) параллельным переносом на (а) единиц вдоль оси
ординат
тригонометрические функции
21

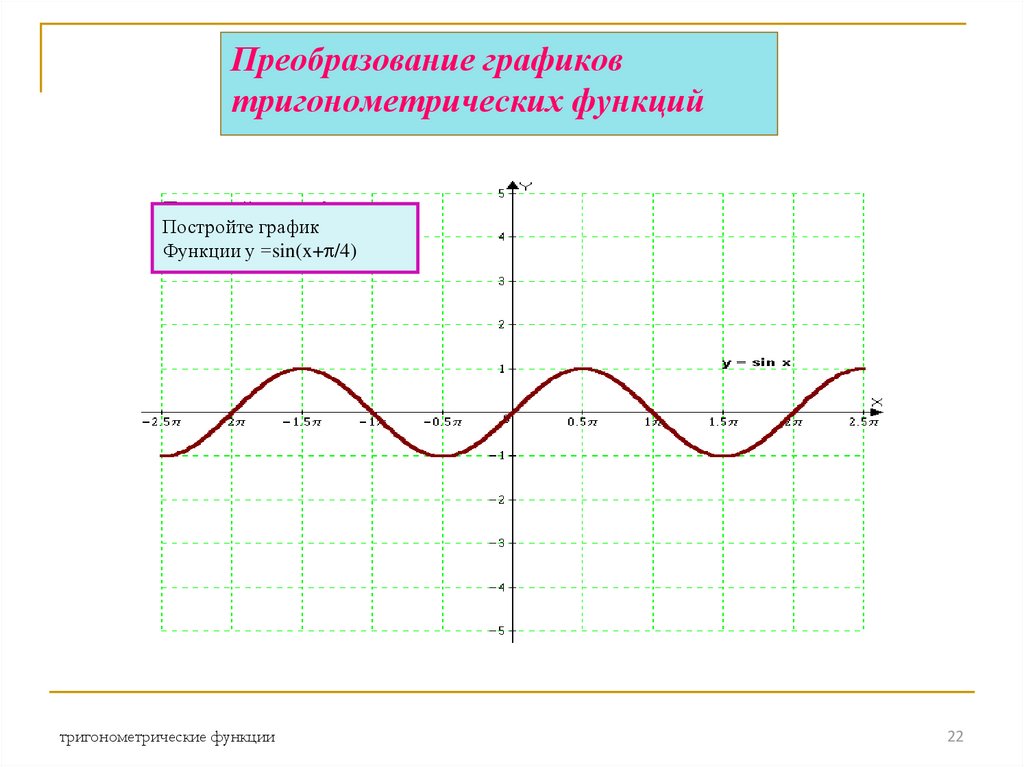
22. Преобразование графиков тригонометрических функций

Постройте график
Функции у =sin(x+ /4)
тригонометрические функции
22

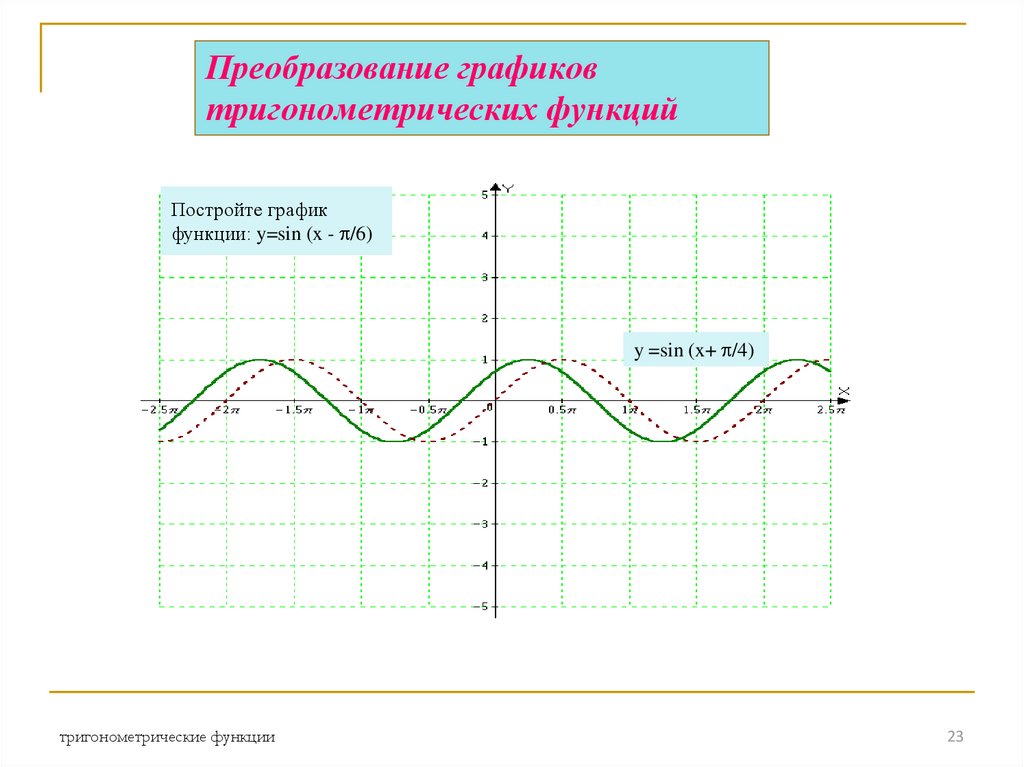
23. Преобразование графиков тригонометрических функций

Постройте график
функции: y=sin (x - /6)
y =sin (x+ /4)
тригонометрические функции
23

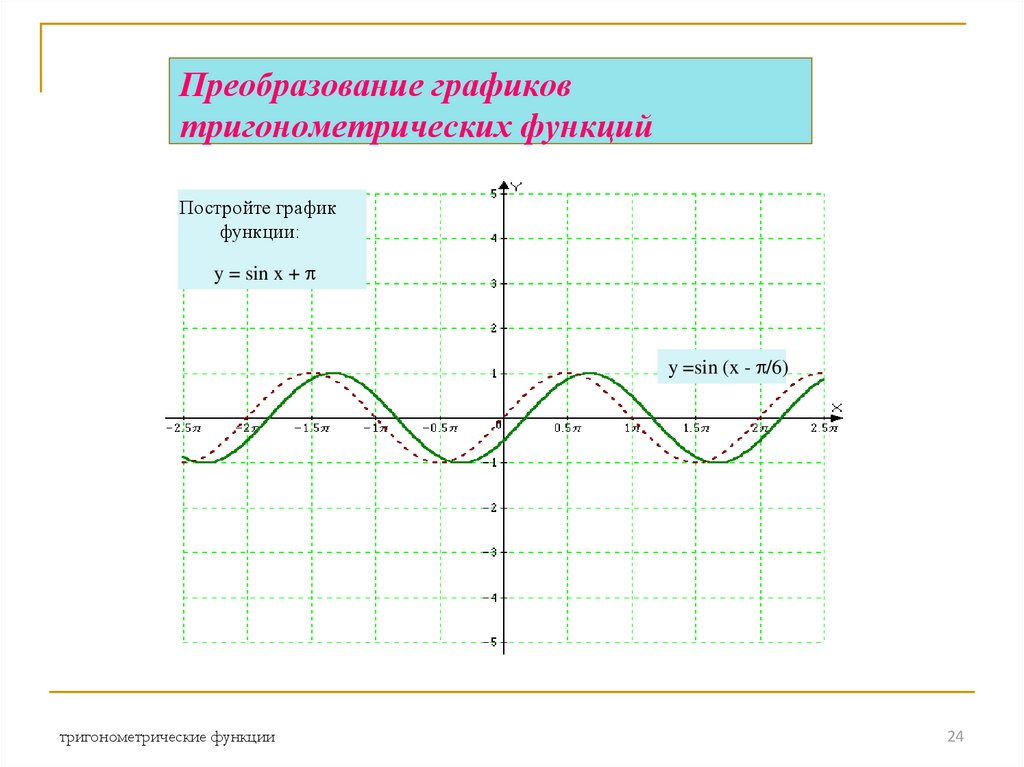
24. Преобразование графиков тригонометрических функций

Постройте график
функции:
y = sin x +
y =sin (x - /6)
тригонометрические функции
24

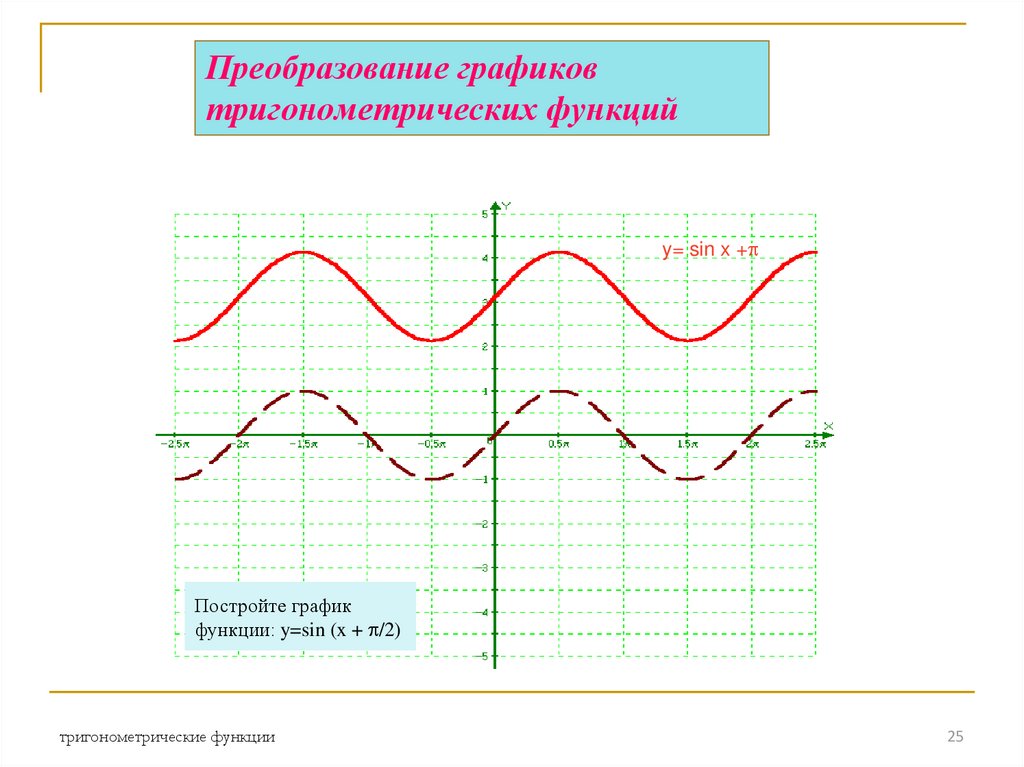
25. Преобразование графиков тригонометрических функций

y= sin x +
Постройте график
функции: y=sin (x + /2)
тригонометрические функции
25

26. Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у =k f (x) получается из графика функции у = f(x)
путем его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x)
путем его сжатия в k раз (при 0<k<1) вдоль оси ординат
тригонометрические функции
26

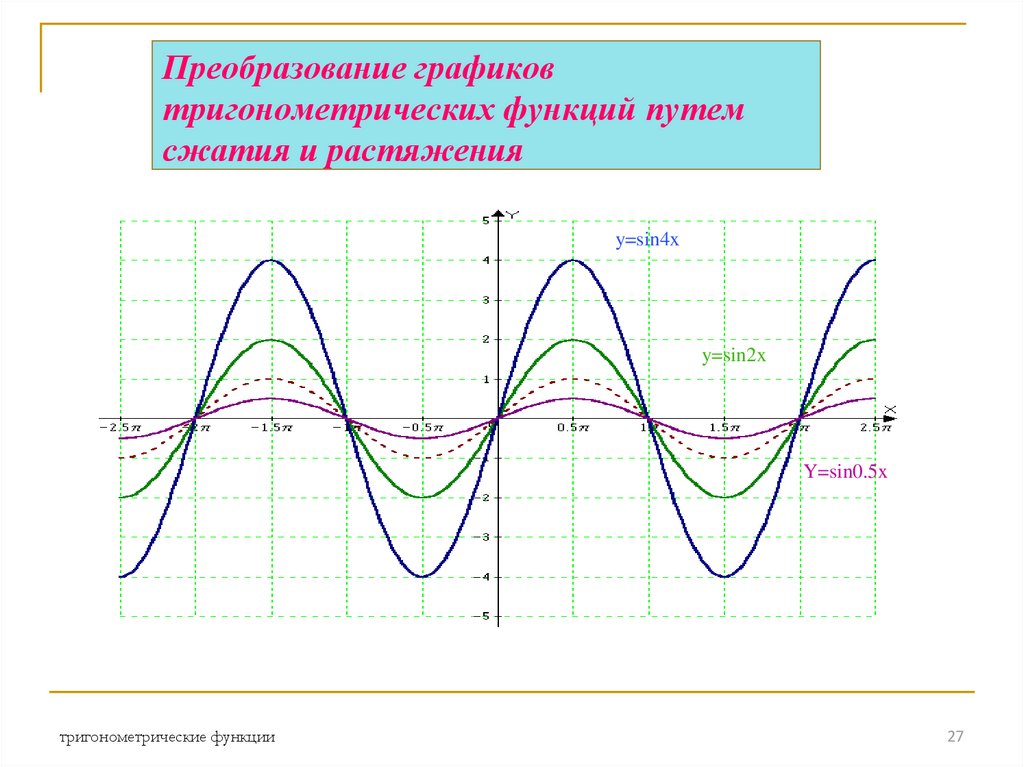
27. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y=sin4x
y=sin2x
Y=sin0.5x
тригонометрические функции
27

28. Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у = f (kx) получается из графика функции у = f(x)
путем его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции у = f(x)
путем его растяжения в k раз (при 0<k<1) вдоль оси абсцисс
тригонометрические функции
28

29. Преобразование графиков тригонометрических функций путем сжатия и растяжения

Графики функций у = -f (kx) и у=-k f(x) получаются из графиков функций
у = f(kx) и y= k f(x) соответственно путем их зеркального отображения
относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
тригонометрические функции
29

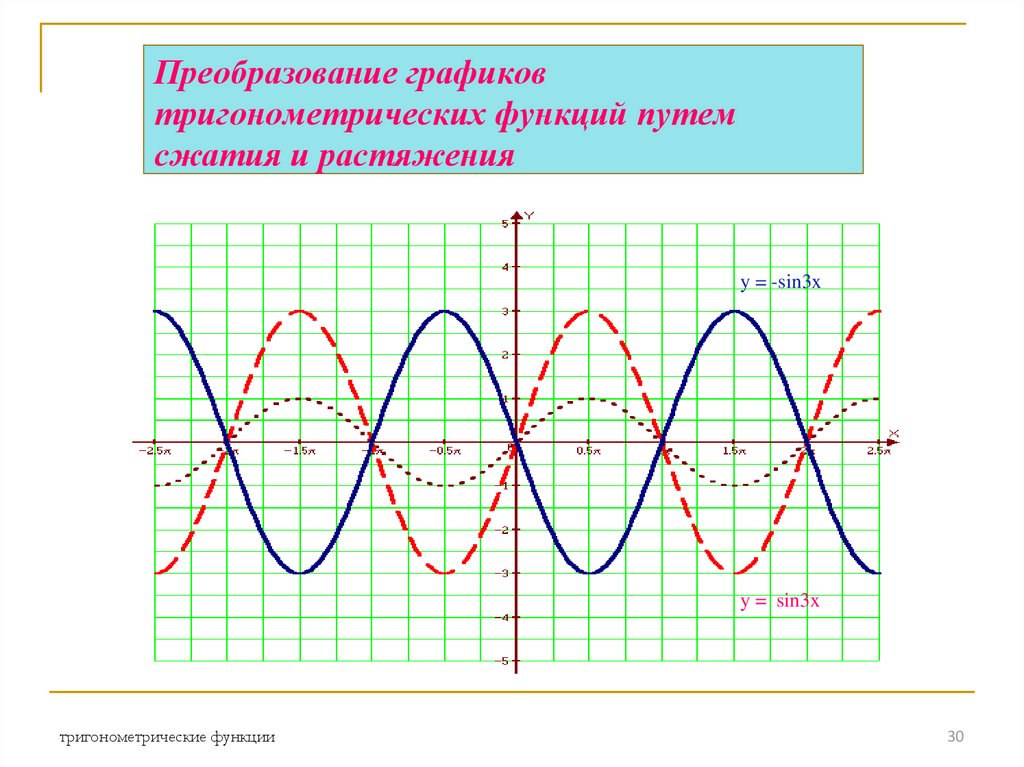
30. Преобразование графиков тригонометрических функций путем сжатия и растяжения

y = -sin3x
y = sin3x
тригонометрические функции
30

31. Преобразование графиков тригонометрических функций путем сжатия и растяжения

График функции у = f (kx+b) получается из графика функции у = f(x)
путем его параллельного переноса на (-в/k) единиц вдоль оси абсцисс и
путем сжатия в k раз (при k>1) или растяжения в k раз ( при 0<k<1) вдоль
оси абсцисс
f ( kx+b) = f ( k( x+b/k))
тригонометрические функции
31