Похожие презентации:
Основы теории нечетких множеств
1.
§5. ОСНОВЫ ТЕОРИИ НЕЧЕТКИХМНОЖЕСТВ
2.
5.1. ОПИСАНИЕ НЕЧЕТКИХ МНОЖЕСТВ,ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ
И ОПЕРАЦИИ НАД НЕЧЕТКИМИ
МНОЖЕСТВАМИ
3.
Определение.Под
нечетким
множеством понимается множество для
которого
невозможно
задать
строгих
границ.
4.
ПустьV
–
полное
множество,
охватывающее всю предметную область.
Нечеткое множество F (оно фактически
является подмножеством V, но принято
говорить о нем как о множестве) определяется
через функцию принадлежности
F (u ) (u –
элемент множества V).
Эта функция отображает элементы и
множества V на множество чисел в интервале
от 0 до 1, которые указывают степень
принадлежности каждого элемента нечеткому
множеству F.
5.
Если такое множество V состоит изконечного числа элементов,
u1, u 2 , u n , то
нечеткое множество F можно представить в
следующем виде:
F
F u1
u1
F u 2
u2
...
F u n
un
n
F ui
i 1
ui
6.
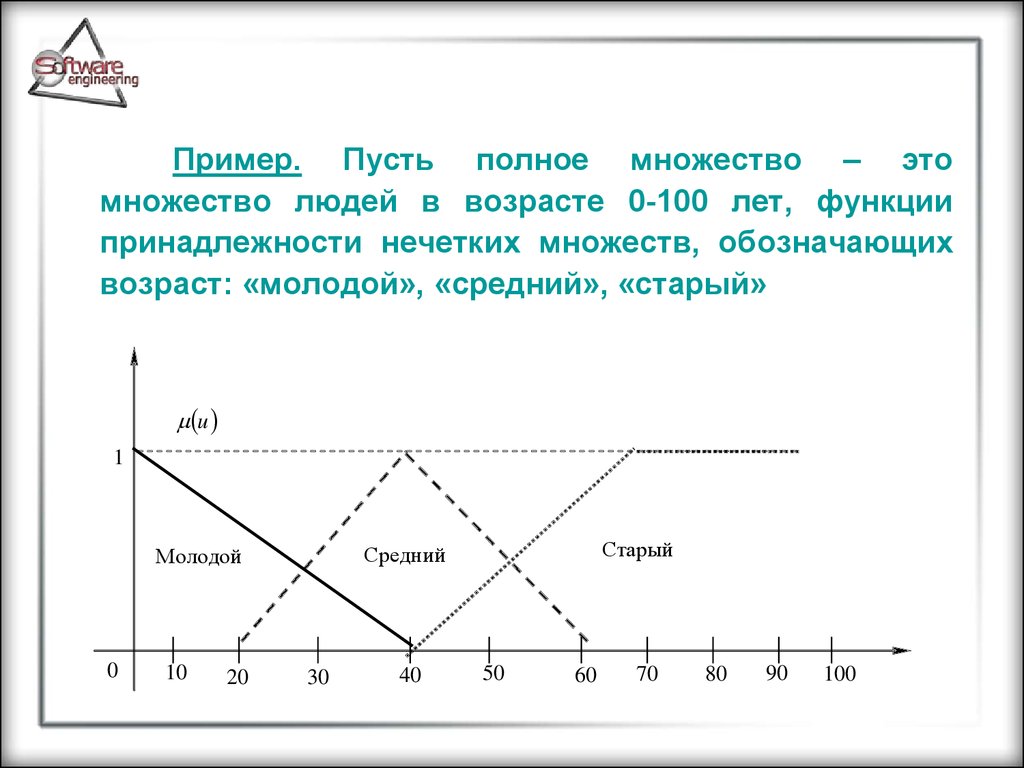
Пример. Пусть полное множество – этомножество людей в возрасте 0-100 лет, функции
принадлежности нечетких множеств, обозначающих
возраст: «молодой», «средний», «старый»
u
1
0
10
20
Старый
Средний
Молодой
30
40
50
60
70
80
90
100
7.
Вслучае
непрерывного
используется интегральное
совокупности
F
V
F u i
ui
множества
V
представление
8.
Если определить множества возрастов какдискретные,
отслеживая
только
позиции,
соответствующие десятилетиям, то множества
могут быть представлены в следующем виде:
молодой молодой u
средний средний u
старый старый u
1 1 0,8 0,3
0 10 20 30
0.5 1 0.5
30 40 50
0.4 0.8 1
1
1
50 60 70 80 90
9. Операции над нечеткими множествами
1. Дополнение множества1 F u i
F
i 1
ui
n
или
F 1 F u
2. Объединение множеств
n
F G
i 1
F u G u
ui
или
F G u F u G u ,
3. Пересечение множеств
n
F u i G u i
i 1
ui
F G
или F G u F u G u ,
10. Пример.
0.2 0.7 11
1
молодой молодой u
...
20 30 40 50
90
1 1 0.8 0.5 1 0.5
молодой средний молодой средний u
0 10 20 30 40 50
молодой средний м олодой средний u 0.3
30
11.
5.2. НЕЧЕТКИЕ ОТНОШЕНИЯ12.
Определение. Нечетким отношением Rмежду некоторой проблемной областью (полным
множеством U) и другой областью (полным
множеством V) называется нечеткое подмножество
прямого
произведения
UXV,
определяемое
следующим образом:
n
m
R
i 1 j 1
R ui , v j
u , v
i
j
U u1 , u 2 ....u n , V v1 , v 2 ...v m
13.
Допустим, что существует знание правиттипа «если F, то G», использующее нечеткие
G V
множества F U
и
, тогда один из
способов построения нечеткого отношения из
соответствующей области множества U в области
множества V состоит в следующем:
n
m
R F G
i 1 j 1
F u i G v i
u , v
i
j
14. Пример:
Пример. ПустьU ={A, B, C, D} - множество людей, а
–
это
множество
штанг
различного
веса,
тогда
определим
следующим образом нечеткие множества: F –
множество сильных людей и G – множество
штанг большого веса.
15.
16.
5.3. СВЕРТКА ОТНОШЕНИЙ17.
Для построения полноценного выводанеобходимо определить не только понятие
отношения, но и правило перехода от одного
отношения к другому, которое базируется на
понятии свертки отношений.
Определение.
Сверткой
отношений
называется правило перехода от одного
отношения к другому, т.е. пусть R – нечеткое
отношение между областью U и областью V, а
S – нечеткое отношение между V и W, тогда
нечеткое отношение между U и W определяется
как свертка отношений R и S
18.
nR S V
i 1 k 1
v j v
R u i , v j S v j , wk
u , w
i
k
Символ « » обозначает минимаксную
свертку, определяемую для выводов с
помощью цепочки правил. v – взятие max
для всех , - взятие min для каждой пары.
19.
Пример. Пусть задано множество чиселмышечной
массы
различного объема и на нем
определено
нечеткие множество H большой мышечной
массы.
-
Множество
как
и
в
предыдущем примере, это множество штанг
различного веса, на котором определено
нечеткое множество F не маленьких весов.
20.
21.
22.
23.
5.4. ПОСТРОЕНИЕ НЕЧЕТКОГО ВЫВОДА24.
Традиционныйдедуктивный
вывод
(называемый правило определения) – это
вывод Q из P (факта) по правилу P Q
Это записывается так
P Q
P
.
Q
25.
Это же обозначение используется вслучаях нечетких дедуктивных выводов, если
знания – это нечеткие множества а именно
F , G, F ' , G' вывод G ' из F ' по правилу
записывается так: F G
F G
P'
'
Q
.
26.
Множества F и F' не обязательно совпадают.Если F и F' близки друг к другу, то их можно
сопоставить и получить вывод
в области их
совпадения.
Конкретно нечеткие выводы представляются
следующим образом. Вывод
определяется из
'
сверткиGмножества
и отношения R.
m
G V
'
j 1
u i V
F u i R u i , v j
vj
F , F ' V , G, G ' V v1 , v2 , vm





























 Математика
Математика Информатика
Информатика








