Похожие презентации:
Разложение вектора по трем некомпланарным
1. Разложение вектора по трем некомпланарным.
12.
Разложение вектора по трем некомпланарным векторам.Если вектор представлен в виде
p = xa + yb + zc
z - некоторые числа, то говорят, что вектор
разложен по векторам a , b и c. Числа x, yи z
x ,y
где
p
и
называются коэффициентами разложения.
Теорема о разложении вектора по трем некомпланарным
векорам.
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
2
3.
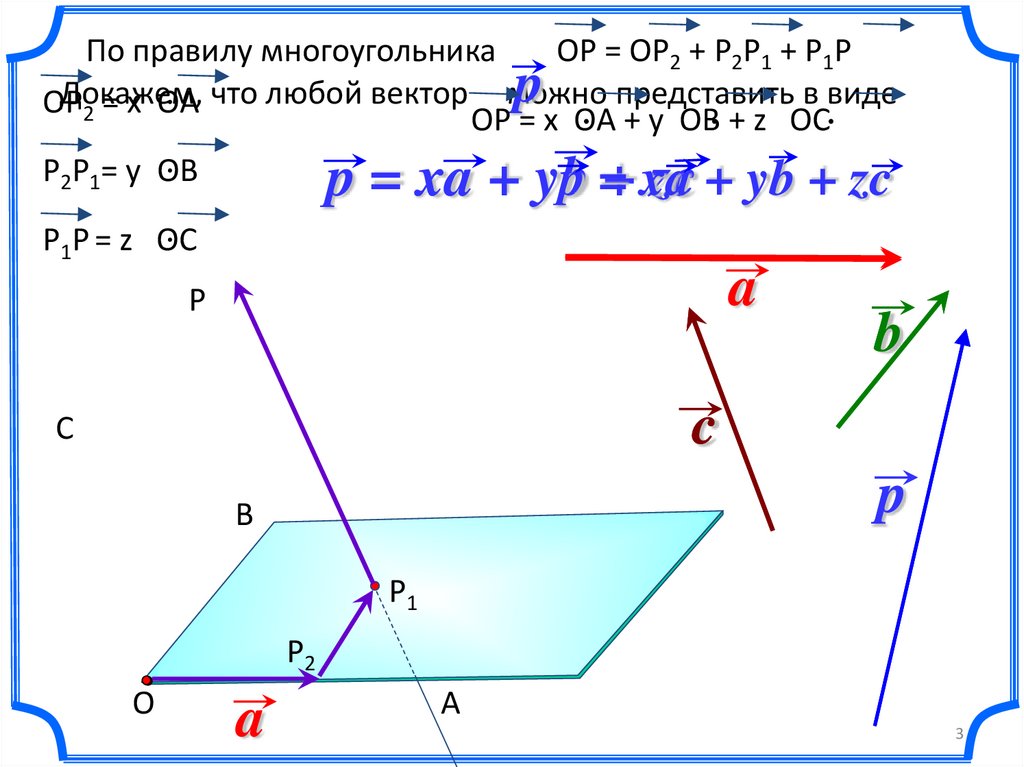
По правилу многоугольникаОР = ОР2 + Р2Р1 + Р1Р
Докажем,
представить в виде
что любой вектор ОРможно
ОР
2 = x OA
= x OA
+ y OB + z OC
Р2Р1= у OВ
p = xa + yb + zc
p
p = xa + yb + zc
Р1Р = z OC
a
P
b
c
C
p
B
P1
P2
O
a
A
3
4.
Докажем теперь, что коэффициенты разложенияопределяются единственным образом. Допустим, что это не так
и существует другое разложение вектора
–
p = xa
x1a++yb
y1b+ +zcz1c
Это равенство выполняется
только тогда,
когда
o = (x – x1)a + (y – y1)b + (z – z1)c
Если предположить, например, что
z z1, то
из
0 этого
o
o
o
x x1 y y1
равенства можно найти с
a
b
z z1
z z1
a , b икомпланарны.
c
Тогда векторы
Это противоречит
условию теоремы. Значит, наше предположение не верно,
и x x1 , y y1 , z Следовательно,
z1.
коэффициенты
p xa ybопределяются
zc
разложения
единственным образом.
4
5.
6.
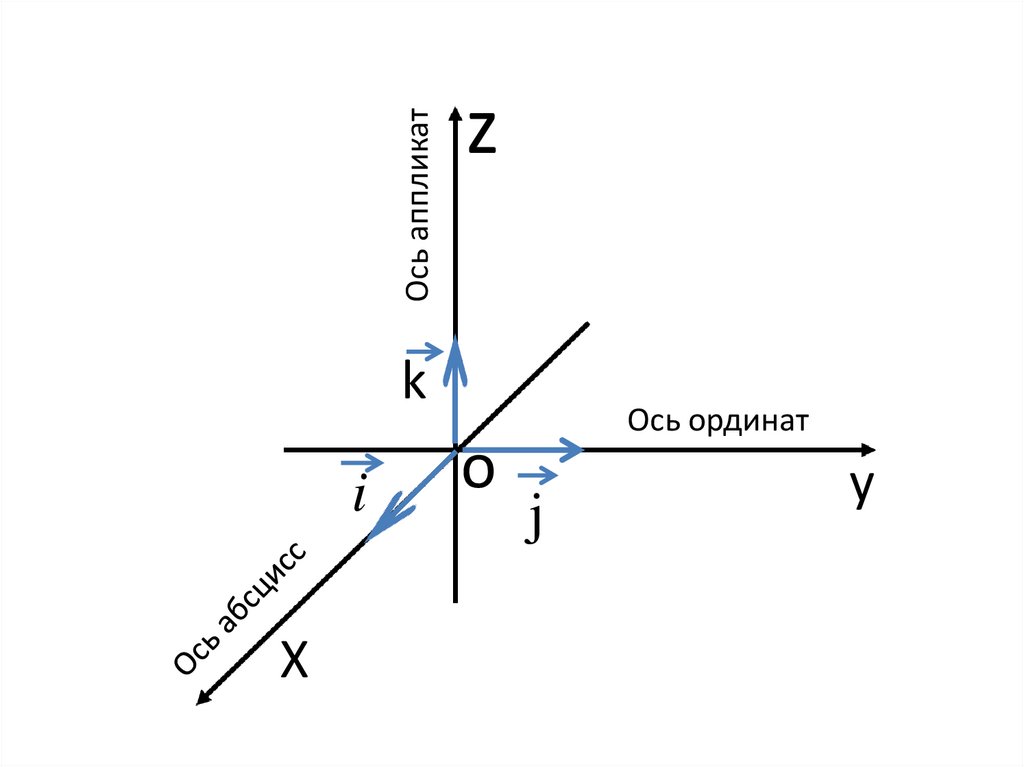
7. Как задать прямоугольную систему координат в пространстве?
1. Выбрать точку пространства2. Провести через неё 3 попарно
перпендикулярные прямые
3. Указать стрелкой направление
4. На каждой оси выбрать единицу
измерения
8.
Ось аппликатz
k
i
X
o
Ось ординат
j
у
9. Запишем в тетради:
ОХ – ось абсциссОУ – ось ординат
OZ – ось аппликат
i, j, k – единицы измерения
(координатные векторы)
О – начало координат
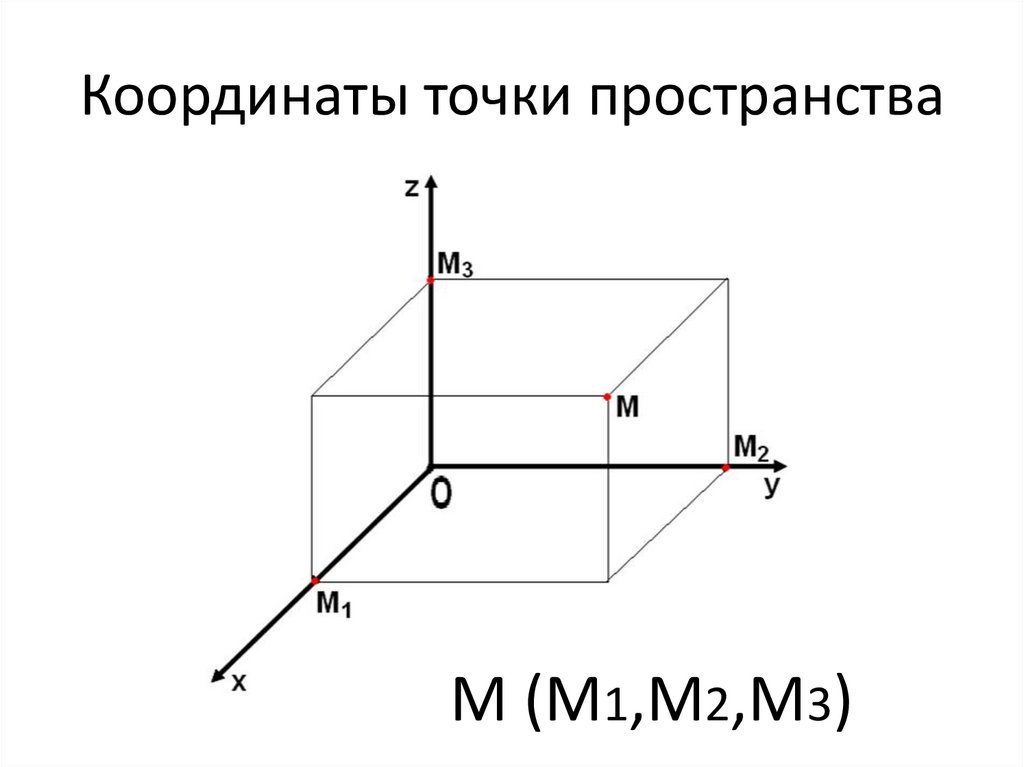
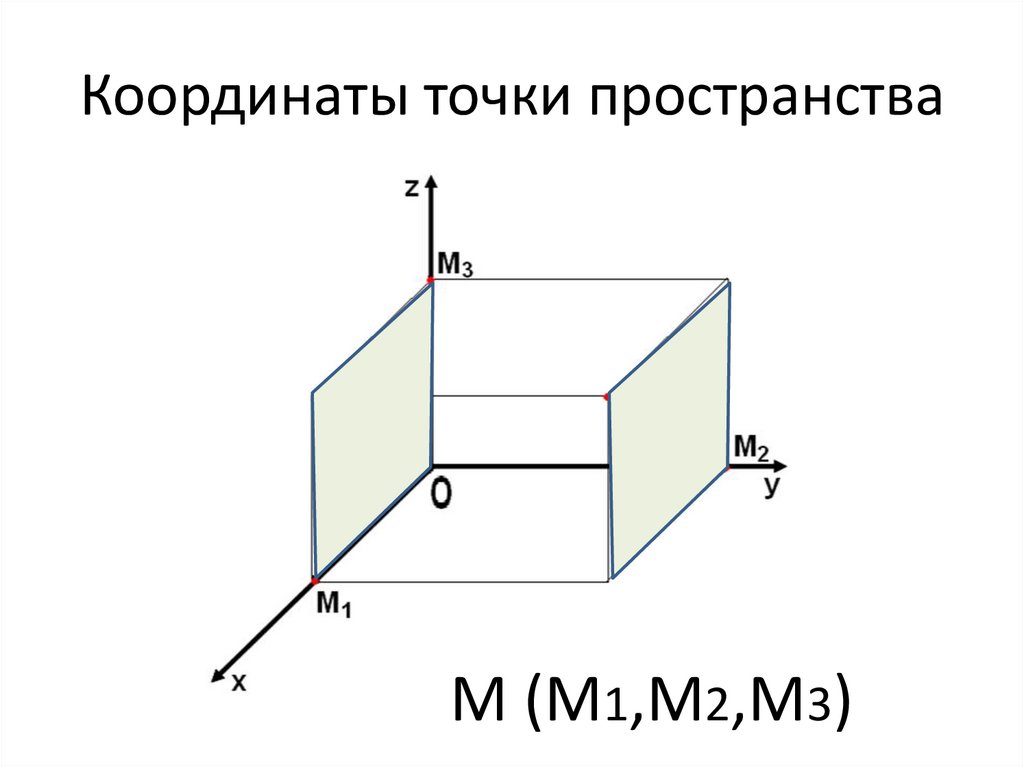
10. Координаты точки пространства
М (М1,М2,М3)11. Координаты точки пространства
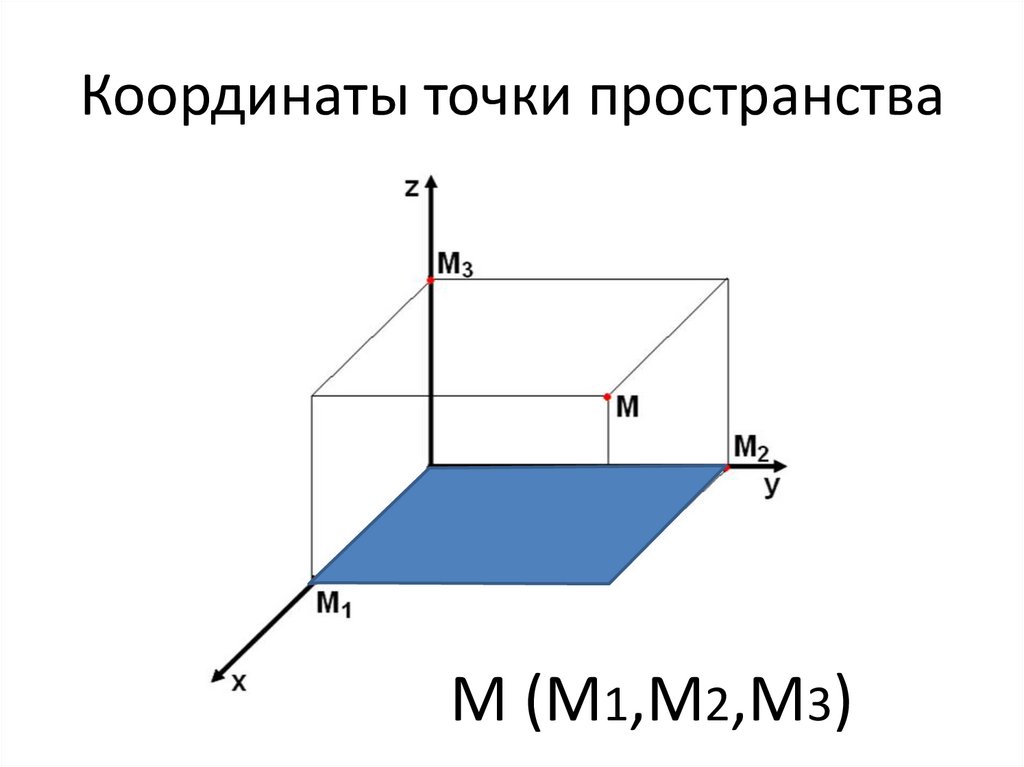
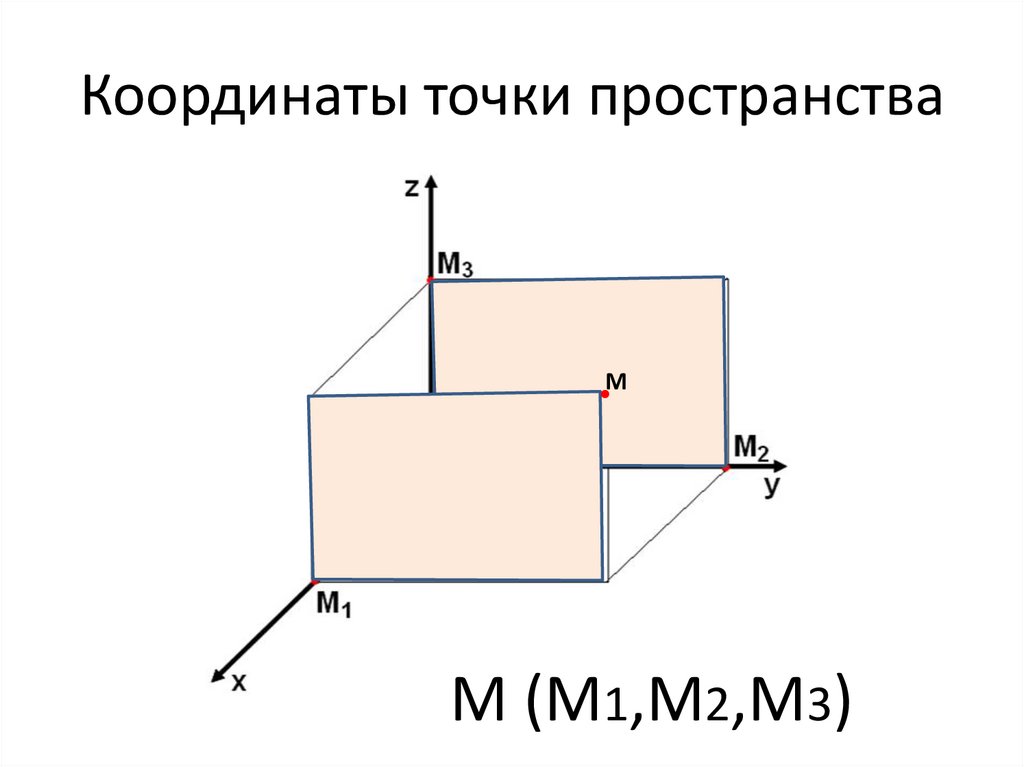
М (М1,М2,М3)12. Координаты точки пространства
М (М1,М2,М3)13. Координаты точки пространства
ММ (М1,М2,М3)
14.
- Чтобы определитькоординаты токи в
пространстве, надо через
точку провести плоскости
параллельно осям.
15.
1.Если М2.Если М
3.Если М
4.Если М
5.Если М
6.Если М
ОХУ, то z=0
OXZ, то у=0
OУZ, то X=0
ОХ, то У=0 и Z=0
OУ, то Х=0 и Z=0
OZ, то Х=0 и У=0
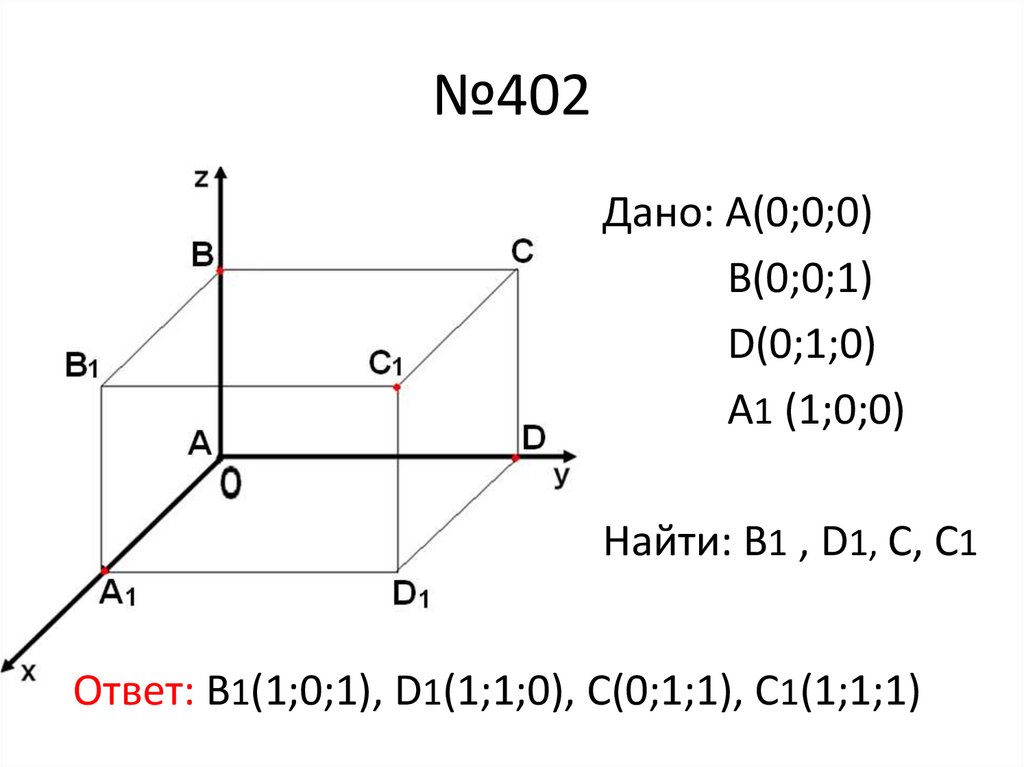
16. №402
Дано: А(0;0;0)В(0;0;1)
D(0;1;0)
A1 (1;0;0)
Найти: В1 , D1, С, С1
Ответ: В1(1;0;1), D1(1;1;0), С(0;1;1), С1(1;1;1)
17. Домашнее задание:
1) п. 46,2) Выполнить конспект презентации
3) №401








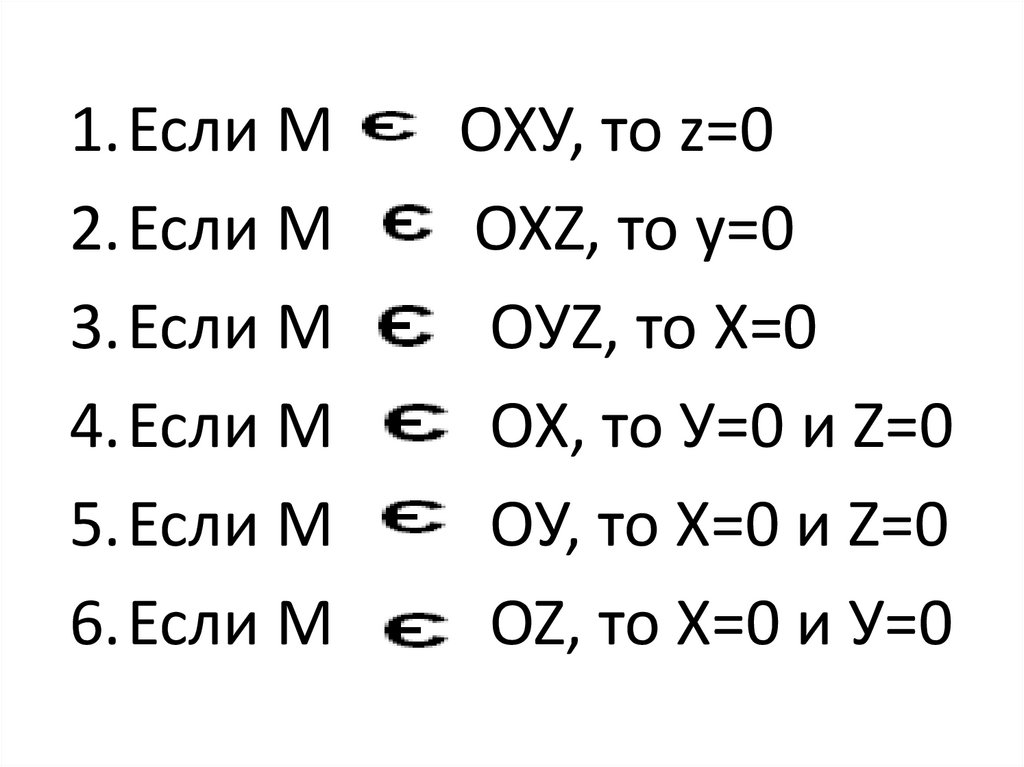

 Математика
Математика








