Методика решения задач ЕГЭ по теме «системы логических уравнений»

1.

Учитель информатики
Шахова Е.А.
ГБОУ «Гимназия №1
им. А.С. Пушкина»
Севастополь, 2017

2.

Формулировка задания
Сколько существует различных наборов значений
логических переменных х1, х2,… (y1, y2, …), которые
удовлетворяют всем перечисленным ниже условиям:
…(система логических уравнений)
В ответе не нужно перечислять все различные наборы
х1, х2, … (y1, y2, …), при которых выполняется
данная система равенств. В качестве ответа
необходимо указать количество таких наборов

3.

Спецификация задания №23
согласно КИМ в 2017 ( «ФИПИ»)
Характеристика
Значение
Что проверяется
Умение строить и преобразовывать
логические выражения
Требования к проверяемым Высказывания, логические операции,
элементам содержания
кванторы, истинность высказывания
Проверяемые требования к Вычислять логическое значение
уровню подготовки
сложного высказывания по известным
значениям элементарных высказываний
Уровень сложности
Высокий (единственный в 1-й части)
Максимальный балл
1
Примерное время
выполнения
10 мин

4.

Особенности решения
• Задание сложное, его невозможно
формализовать;
• Большое количество приемов и методов
решения;
• Большая сложность при маленьком
количестве баллов (лучше решить №24,
чем №23);
• Требует базовых знаний по
комбинаторике.

5.

Необходимые знания и умения
• Базовые и дополнительные логические
операции;
• Законы алгебры логики;
• Структуры данных – деревья;
• Метод замены переменных;
• Метод отображения (динамическое
программирование);
• Основы комбинаторики;
• Навыки преобразования и анализа логических
выражений.

6.

Условные обозначения (в порядке
приоритета операций)
• отрицание (НЕ) : ¬ A , А , not A
• конъюнкция (И) : A ˄ B , A B, AB, А&B,
A and B
• дизъюнкция (ИЛИ) : A ˅ B , A+ B, A | B,
А or B
• импликация (следствие) : А → B
• эквивалентность (равенство): A ⇔ В,
A ∼ B, A ≡ B
• исключающее «или» (сложение по модулю 2) :
A⊕ B , A xor B

7.

Базовые логические операции НЕ, И, ИЛИ
А
не А
0
1
1
0
A
0
0
1
1
B
0
1
0
1
АиB
0
0
0
1
A
0
0
1
1
B
0
1
0
1
А или B
0
1
1
1
Дополнительные логические операции
Исключающее ИЛИ
A
0
0
1
1
!
B
0
1
0
1
А⊕B
0
1
1
0
Импликация
A
0
0
1
1
B
0
1
0
1
А→B
1
1
0
1
Эквивалентность
A
0
0
1
1
B
0
1
0
1
Необходимо знать и словесное описание операций
А≡B
1
0
0
1

8.

Основные законы логики
Свойства логических операций
И
Название
Переместительный
Сочетательный
Распределительный
ИЛИ
НЕ
Закон в логике
Аналог в алгебре
А˅B=B˅ A
А + B=B + A
А˄B=B˄ A
А * B=B * A
(А ˅ B) ˅ C =А ˅( B˅ C)
(А + B) + C =А +( B+ C)
(А ˄ B) ˄ C =А ˄ ( B˄ C)
(А*B) * C =А *( B* C)
(А ˅ B) ˄ C = (А ˄ C) ˅ (B ˄ C)
(А +B) *C = (А*C) +(B*C)
(А ˄ B) ˅ C = (А ˅ C ) ˄(B˅ C)
Аналога нет

9.

Основные законы логики
Законы де Моргана:
A ⋅B = A + B,
A +B = A ⋅B
Формулы склеивания:
(
)
A ⋅B + A ⋅ B = A ⋅ B + B = A
(A + B) ⋅ (A + B ) = A + (B ⋅ B ) = A
Формулы поглощения:
(
)
A + A ⋅ B = A ⋅ 1+ B = A
A ⋅ (A + B ) = A + (A ⋅ B ) = A
A + A ⋅ B = A ⋅ (1+ B ) + A ⋅ B = A + A ⋅ B + A ⋅ B =
(
)
= A +B⋅ A + A = A +B

10.

Преобразование операций
A →B = A +B = B → A
(A ≡ B) = A ⋅ B + A ⋅ B
(
)
(A ≡ B) = A ⋅ B + A ⋅ B = A ⋅ B ⋅ A ⋅ B = A + B ⋅ (A + B ) =
= A ⋅ A + B ⋅ A + A ⋅B + B ⋅B = B ⋅ A + A ⋅B
(A ≡ B ) = A ⋅ B + A ⋅ B = (A ≡ B) = A ⊕ B

11.

Метод замены переменных
Применяется,
если
можно
выделить
одинаковые
выражения в уравнениях, между которыми нет общих
переменных.
ПРИМЕР:
((x1 ≡ x2) \/ (x3 ≡ x4)) /\ (¬(x1 ≡ x2) \/ ¬(x3 ≡ x4)) =1
((x3 ≡ x4) \/ (x5 ≡ x6)) /\ (¬(x3 ≡ x4) \/ ¬(x5 ≡ x6)) =1
((x5 ≡ x6) \/ (x7 ≡ x8)) /\ (¬(x5 ≡ x7) \/ ¬(x7 ≡ x8)) =1
((x7 ≡ x8) \/ (x9 ≡ x10)) /\ (¬(x7 ≡ x8) \/ ¬(x9 ≡ x10)) =1
ЗАМЕНА:
t1 =
t2 =
t3 =
t4 =
t5 =
(x1≡ x2)
(x3≡ x4)
(x5≡ x6)
(x7≡ x8)
(x9≡ x10)

12.

Метод замены переменных
Получаем после преобразования
(t1 ∨ t2 ) ∧
(t2 ∨ t3) ∧
(t3 ∨ t4 ) ∧
(t4 ∨ t5) ∧
(t1 ∨ t2 ) = 1 t1 t2 ∨ t1 t2 = 1
(t2 ∨ t3 ) = 1 => t2 t3 ∨ t2 t3 = 1 =>
(t3 ∨ t4) = 1 t3 t4 ∨ t3 t4 = 1
(t4 ∨ t5) = 1 t4 t5 ∨ t4 t5 = 1
Решение в новых переменных (2 набора)
t1
t2
t3
t4
t5
0
1
0
1
0
1
0
1
0
1
t1 ≡ t2 = 1
t2 ≡ t3 = 1
t3 ≡ t4 = 1
t4 ≡ t5 = 1

13.

Метод замены переменных
Для каждой комбинации из 5-ти
значений t1 … t5 существует по 2
решения:
если t1 = 0, то x1 =1, x2 =0
или x1 =0, x2 =1
если t1 = 1, то x1 =1, x2 =1
или x1 =0, x2 =0
t1 = (x1 ≡ x2)
t2 = (x3 ≡ x4)
t3 = (x5 ≡ x6)
t4 = (x7 ≡ x8)
t5 = (x9 ≡ x10)
То есть 2 варианта по 5 переменным дают 25=32 решения,
32+32=64

14.

Метод замены переменных
Для закрепления
Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое
пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015.

15.

Построение дерева вариантов
Сколько существует различных наборов
значений логических переменных х1, х2,…х8,
которые удовлетворяют всем перечисленным
ниже условиям:
Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое
пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015.

16.

Построение дерева вариантов
(x1 ≡ x2 ) ∧ (x1 ≡ x3) = 0
(x2 ≡ x3) ∧ (x2 ≡ x4 ) = 0
(x3 ≡ x4 ) ∧ (x3 ≡ x5) = 0
...
(x6 ≡ x7 ) ∧ (x6 ≡ x8) = 0
ИЛИ
(x1 ≡ x2 ) ∨ (x1 ≡ x3) = 1
(x2 ≡ x3) ∨ (x2 ≡ x4 ) = 1
(x3 ≡ x4 ) ∨ (x3 ≡ x5) = 1
...
(x6 ≡ x7 ) ∨ (x6 ≡ x8) = 1

17.

Построение дерева вариантов
(x1 ≡ x2 ) ∨ (x1 ≡ x3) = 1
(x2 ≡ x3) ∨ (x2 ≡ x4 ) = 1
...
(x6 ≡ x7 ) ∨ (x6 ≡ x8) = 1
Для x1=1 строится точно такое же дерево, только с инвертированными
(противоположными) значениями, поскольку операция эквивалентности
симметрична относительно значений аргументов. Итого решений 34*2=68

18.

Построение дерева вариантов
Плюсы:
- Универсальность (можно использовать всегда);
- Наглядность.
Минусы:
- Громоздкость решения в некоторых случаях;
- Сложность выявить закономерность при больших
размерностях.
!
Вывод: максимально упрощать выражения, при
возможности использовать частные методы
решения и логику.

19.

Метод отображения
(динамическое программирование)
Используется, когда система состоит из
уравнений, отличающихся только индексами.
(x1 ≡ x2 ) ∨ (x1 ≡ x3) = 1
(x2 ≡ x3) ∨ (x2 ≡ x4 ) = 1
...
(x6 ≡ x7 ) ∨ (x6 ≡ x8) = 1

20.

Метод отображения
(динамическое программирование)
(x1 ≡ x2) ∨ (x1 ≡ x3) = 1
x1
x2
X3
0
0
1
1
0
0
1
0
1
1
1
0
Значения пары (x1,x2) определяют
возможные значения переменной x3. Т.к.
другие уравнения аналогичны ,то пары
(x2,x3) влияют на x4 и т.д. Выявим
закономерности получения пар значений
(x1,x2)
00
01
10
11
(x2,x3)
00
01
10
11

21.

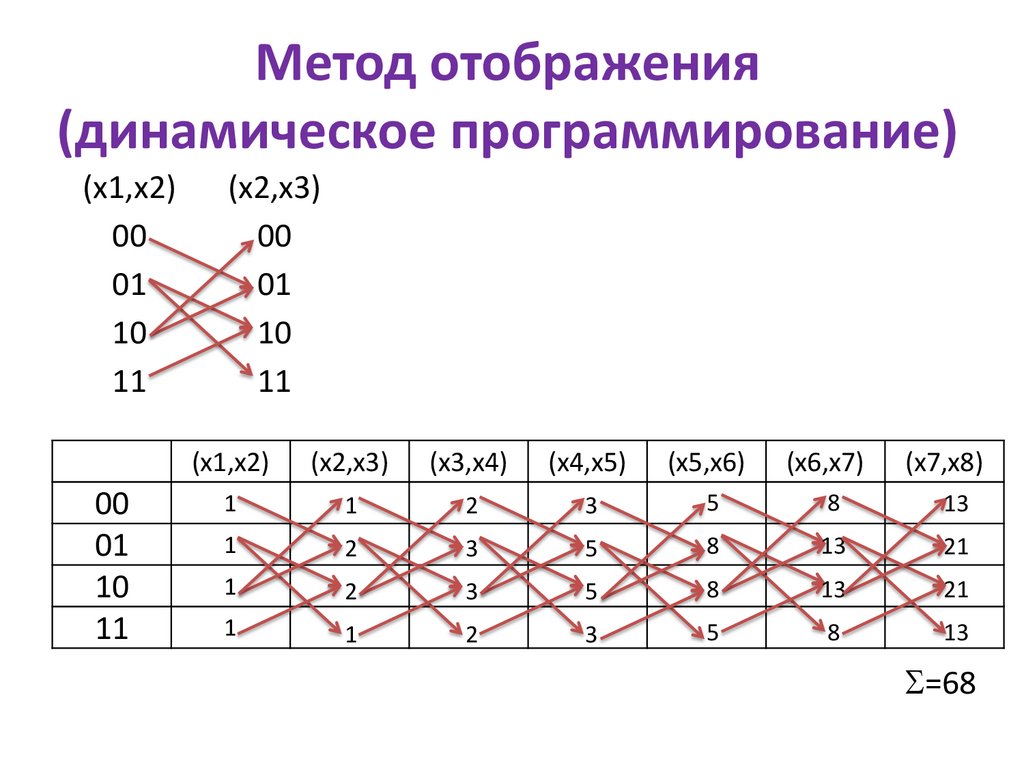
Метод отображения
(динамическое программирование)
(x1,x2)
00
01
10
11
00
01
10
11
(x2,x3)
00
01
10
11
(x1,x2)
(x2,x3)
(x3,x4)
(x4,x5)
(x5,x6)
(x6,x7)
(x7,x8)
1
1
2
3
5
8
13
1
2
3
5
8
13
21
1
2
3
5
8
13
21
1
1
2
3
5
8
13
Σ=68

22.

Метод отображения
(динамическое программирование)
Сложность использования: наличие
ограничений.
x1
0
x2
0
1
1
?
0
1
x3
0
1
0
1
1
0
1
Проблема: Как исключить из таблицы варианты,
которые не удовлетворяют последнему
уравнению.

23.

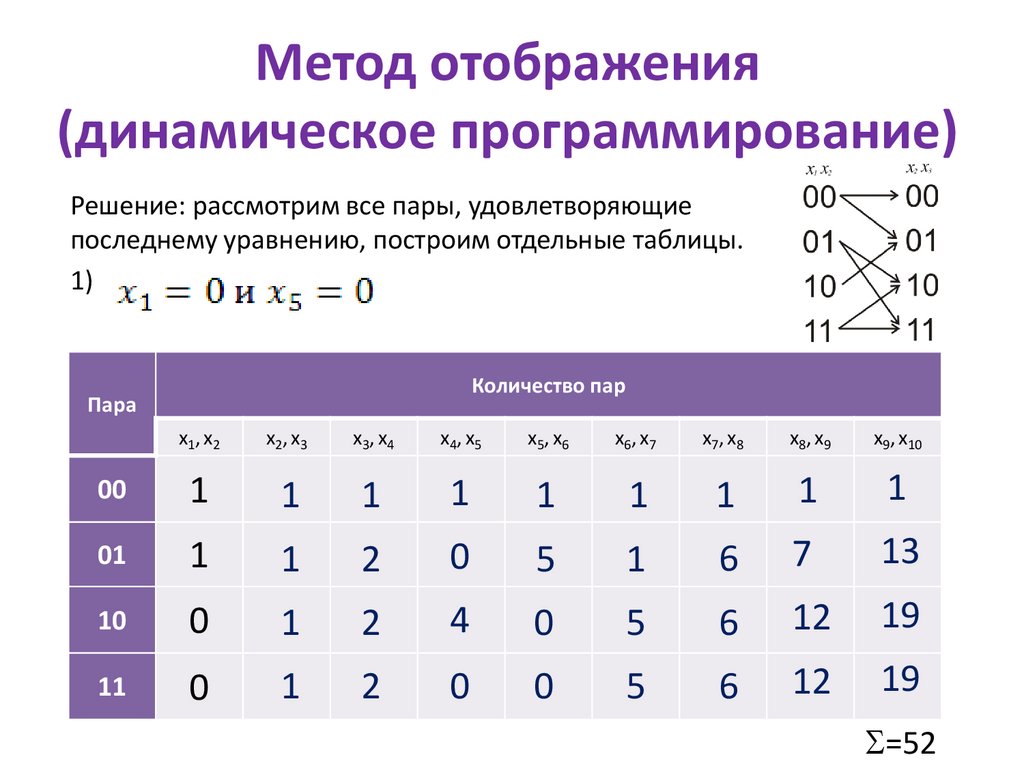
Метод отображения
(динамическое программирование)
Решение: рассмотрим все пары, удовлетворяющие
последнему уравнению, построим отдельные таблицы.
1)
Количество пар
Пара
x1, x2
x2, x3
x3, x4
x4, x5
x5, x6
x6, x7
x7, x8
x8, x9
x9, x10
00
1
1
1
1
1
1
1
1
1
01
1
1
2
0
5
1
6
7
13
10
0
1
2
4
0
5
6
12
19
11
0
1
2
0
0
5
6
12
19
Σ=52

24.

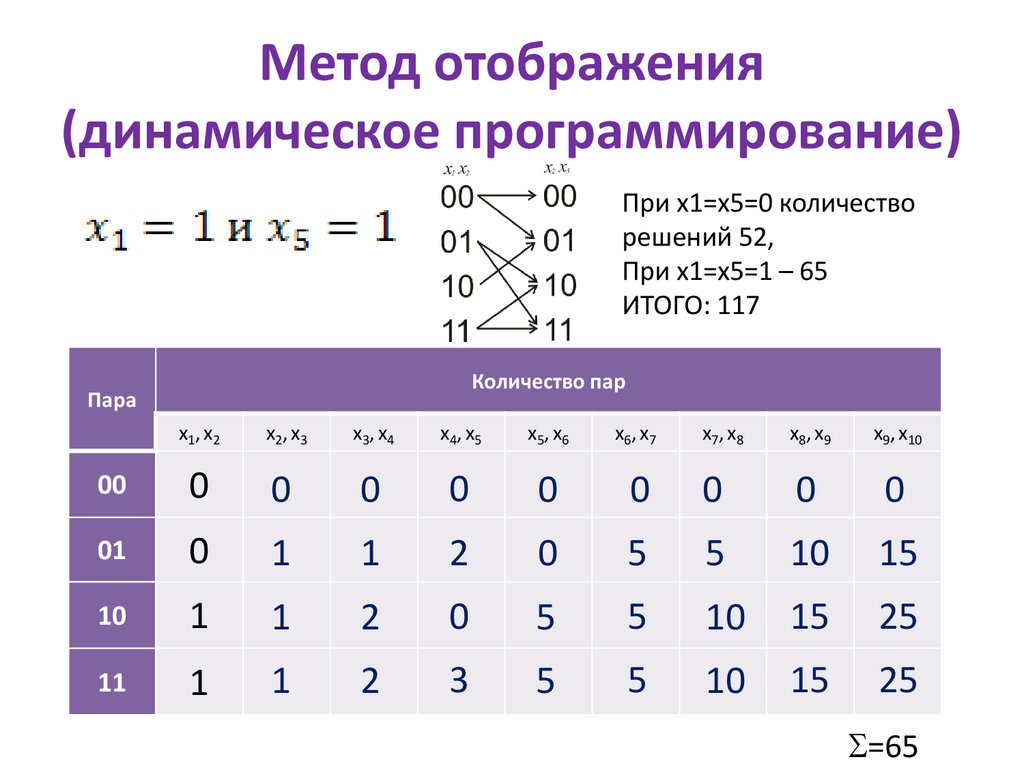
Метод отображения
(динамическое программирование)
При x1=x5=0 количество
решений 52,
При x1=x5=1 – 65
ИТОГО: 117
Количество пар
Пара
x1, x2
x2, x3
x3, x4
x4, x5
x5, x6
x6, x7
x7, x8
x8, x9
x9, x10
00
0
0
0
0
0
0
0
0
0
01
0
1
1
2
0
5
5
10
15
10
1
1
2
0
5
5
10
15
25
11
1
1
2
3
5
5
10
15
25
Σ=65

25.

Задачи
(x1 ≡ x2 ) ∧ ¬(x2 ∨ x3) ∧ (x2 ∨ ¬x3) = 0
1)
(x2 ≡ x3) ∧ ¬(x3 ∨ x4 ) ∧ (x3 ∨ ¬x4 ) = 0
...
(x6 ≡ x7 ) ∧ ¬(x7 ∨ x8) ∧ (x7 ∨ ¬x8) = 0
Ответ: 149
2) (x1 → x2 ) ∧ (x2 → x3) ∧ (x3 → x4 ) ∧ (x4 → x5) = 1
(
) (
) (
) (
)
y1 → y2 ∧ y2 → y3 ∧ y3 → y4 ∧ y4 → y5 = 1
x1 ∨ y1 = 1
) (
)
(
) (
) (
(y1 → y2) ∧ (y 2 → y3) ∧ (y3 → y4) ∧ (y4 → y5) = 1
(x1 ∨ y1) ∧ x1 = 1
3) x1 → x2 ∧ x2 → x3 ∧ x3 → x4 ∧ x4 → x5 = 1
Ответ: 73
Ответ: 5

26.

Задачи
(
(
) ∧ ((x1 ∧ x2) → x3) ∧ (x3 ≡ y1) = 1
) ∧ ((x2 ∧ x3) → x4) ∧ (x4 ≡ y2) = 1
x1 ∨ x2
4)
x2 ∨ x3
...
x6 ∨ x7
x7 ∨ x8
5)
(
) ∧ ((x6 ∧ x7) → x8) ∧ (x8 ≡ y6) = 1
(
) ∧ (y7 ∨ y8) = 1
(x1 ∧ x2 ) ∨ (x3 ∧ ( x1 → x2) ) ∨ (x1 ∧ y1) = 0
(x2 ∧ x3) ∨ (x4 ∧ ( x2 → x3) ) ∨ (x2 ∧ y2) = 0
x6 ∧ x7 ∨ x8 ∧ ( x6 → x7) ∨ (x6 ∧ y6) = 0
x7 ∧ x8 ∨ (x7 ∧ y7) = 0
x8 ∧ y8 = 0
(
(
) (
)
)
Ответ: 165
Ответ: 73

27.

Список использованных источников
1) Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных
вариантов по демоверсии на 2016 год: учебно-методическое
пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону:
Легион, 2015.
2) Презентация Лимаренко Андрея Ивановича, учителя информатики
гимназии 446 на тему «Мастер класс: Логические задачи. Подготовка
к ЕГЭ, В15»
3) Презентация Мирончик Ел. А., Мирончик Ек. А. на тему «Системы
логических уравнений. Метод отображения.» г. Новокузнецк, 2012.
4) Презентация Вишневской М.П., МАОУ «Гимназия №3» на тему
«Решение задания В15 (системы логических уравнений)» 2013 г., г.
Саратов .