Аксиомы и теоремы

1.

Аксиомы и теоремы

2.

Аксиома – утверждение, принимаемое без
доказательств.
«Аксиос»- «утверждение, не вызывающее
сомнений»

3.

Теорема – утверждение, которое
доказывается.
Правильность утверждения о свойстве
геометрической фигуры устанавливается путем
рассуждения. Это рассуждение и называют
доказательством.

4.

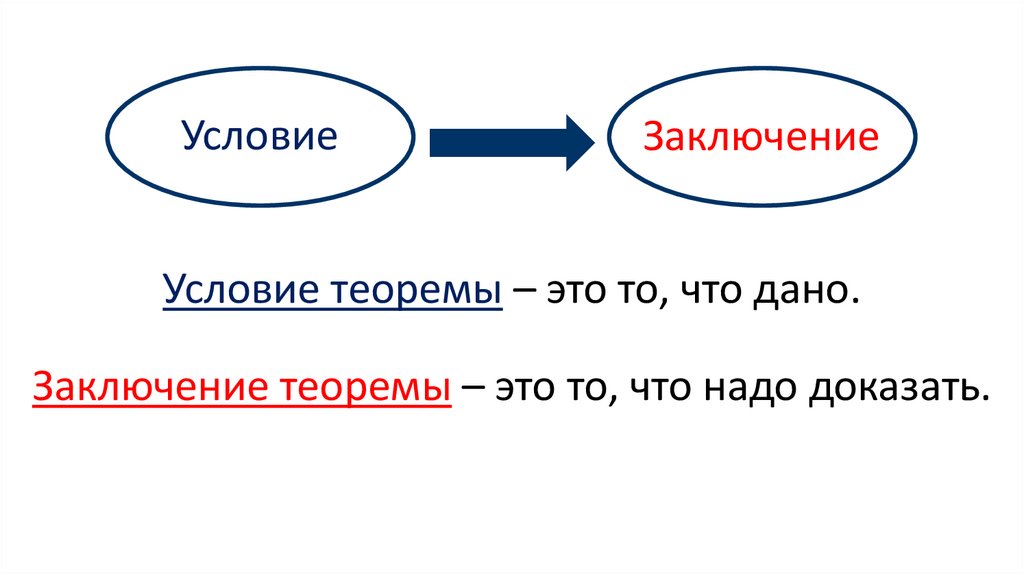
Условие
Заключение
Условие теоремы – это то, что дано.
Заключение теоремы – это то, что надо доказать.

5.

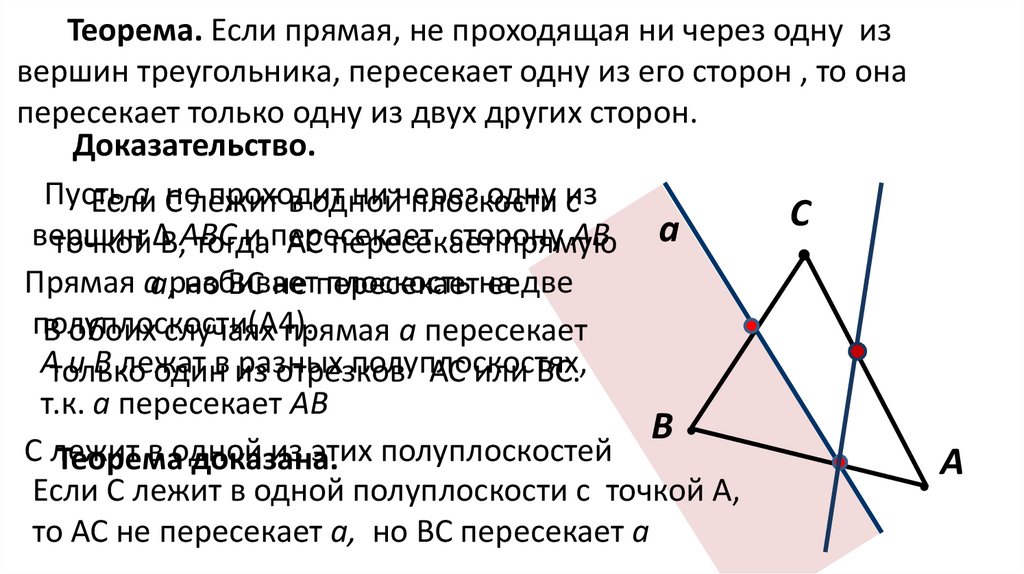
Если прямая, не проходящая ни через одну из
вершин треугольника, пересекает одну из его сторон ,
то она пересекает только одну из двух других сторон.
Условие: прямая, не проходящая ни через одну из
вершин треугольника, пересекает одну из его сторон.
Заключение: она пересекает только одну из двух
других сторон.

6.

Теорема. Если прямая, не проходящая ни через одну из
вершин треугольника, пересекает одну из его сторон , то она
пересекает только одну из двух других сторон.
Доказательство.
Пусть
а С
нележит
проходит
ни через
одну из
Если
в одной
плоскости
с
C
а
вершин
и пересекает
сторону
АВ
точкой∆В,АВС
тогда
АС пересекает
прямую
Прямая аа,разбивает
плоскость на
но ВС не пересекает
еедве
полуплоскости(А4).
В обоих случаях прямая а пересекает
Атолько
и В лежат
разных
полуплоскостях,
одинв из
отрезков
АС или ВС.
т.к. а пересекает АВ
В
С лежит
в одной
из этих полуплоскостей
Теорема
доказана.
А
Если С лежит в одной полуплоскости с точкой А,
то АС не пересекает а, но ВС пересекает а

7.

Спасибо за внимание
Конспект запишите в тетрадь!