Похожие презентации:
Аксиомы стереометрии
1.
2.
- Что такое геометрия?Геометрия – наука о свойствах геометрических фигур
«Геометрия» - (греч.) – «землемерие»
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором
изучаются свойства фигур на плоскости.
- Основные понятия планиметрии?
Основные понятия планиметрии:
А
точка
а
прямая
3.
- раздел геометрии,в котором
изучаются свойства
фигур в
пространстве
4.
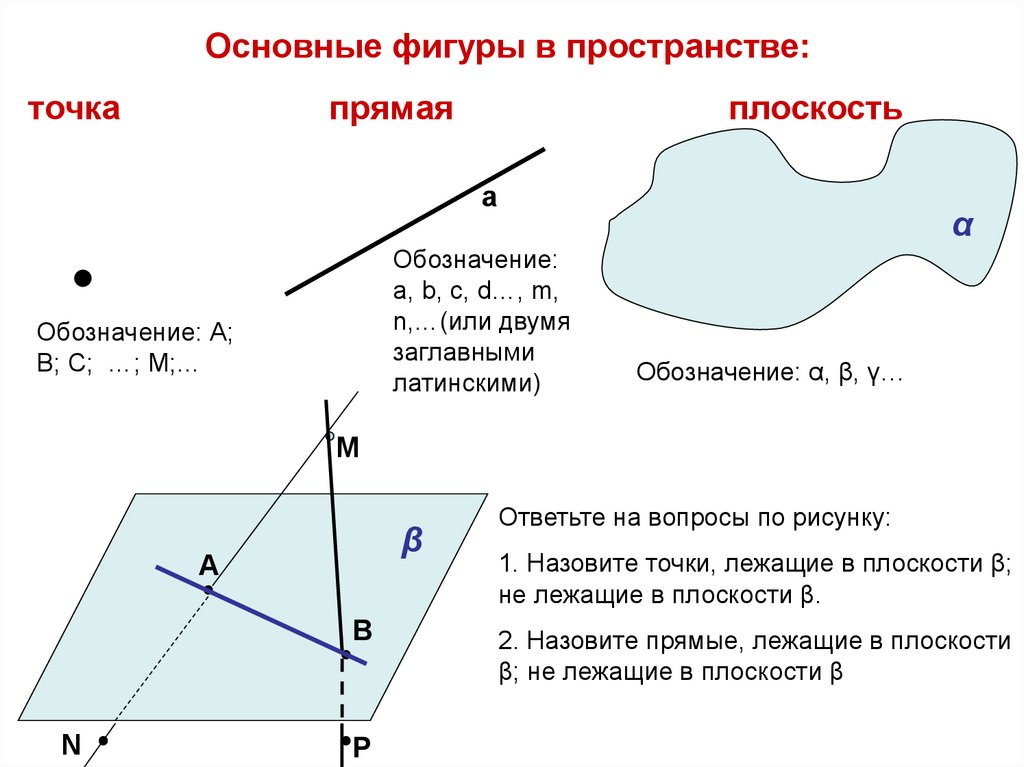
Основные фигуры в пространстве:точка
прямая
плоскость
а
α
Обозначение:
a, b, с, d…, m,
n,…(или двумя
заглавными
латинскими)
Обозначение: А;
В; С; …; М;…
Обозначение: α, β, γ…
М
β
А
В
N
Р
Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β;
не лежащие в плоскости β.
2. Назовите прямые, лежащие в плоскости
β; не лежащие в плоскости β
5.
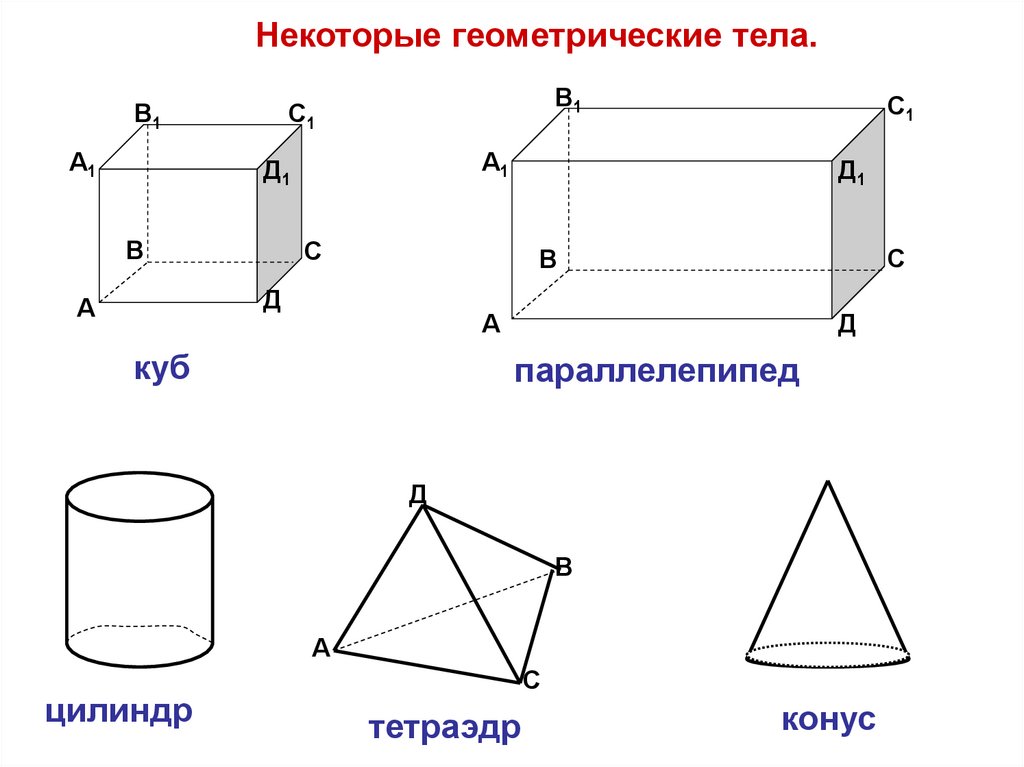
Некоторые геометрические тела.В1
А1
В1
С1
А1
Д1
В
Д1
С
С
В
Д
А
С1
А
куб
Д
параллелепипед
Д
В
А
цилиндр
С
тетраэдр
конус
6.
Практическая работа.В1
А1
С1
1. Изобразите в тетради куб (видимые
линии – сплошной линией, невидимые –
пунктиром).
2. Обозначьте вершины куба заглавными
буквами АВСДА1В1С1Д1
Д1
3. Выделите цветным карандашом:
-вершины А, С, В1, Д1
В
А
С
Д
-отрезки АВ, СД, В1С, Д1С
-диагонали квадрата АА1В1В
7.
- Что такое аксиома?Аксиома – это утверждение о свойствах
геометрических фигур, принимается в качестве
исходных положений, на основе которых доказываются
далее теоремы и вообще строится вся геометрия.
Аксиомы планиметрии:
- через любые две точки можно провести прямую и
притом только одну.
-из трех точек прямой одна, и только одна, лежит
между двумя другими.
-имеются по крайней мере три точки, не лежащие на
одной прямой…
8.
ВА
α
С
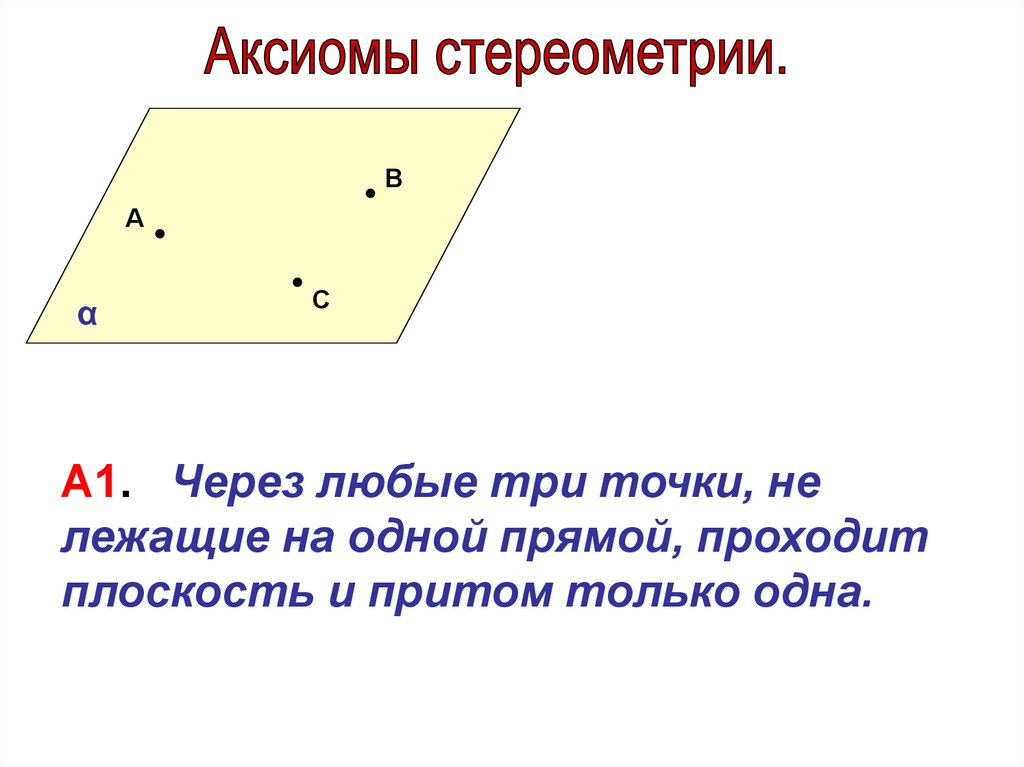
А1. Через любые три точки, не
лежащие на одной прямой, проходит
плоскость и притом только одна.
9.
Если ножки стола не одинаковы по длине, то стол стоит на трехножках, т.е. опирается на три «точки», а конец четвертой ножки
(четвертая точка) не лежит в плоскости пола, а висит в воздухе.
10.
ВА
α
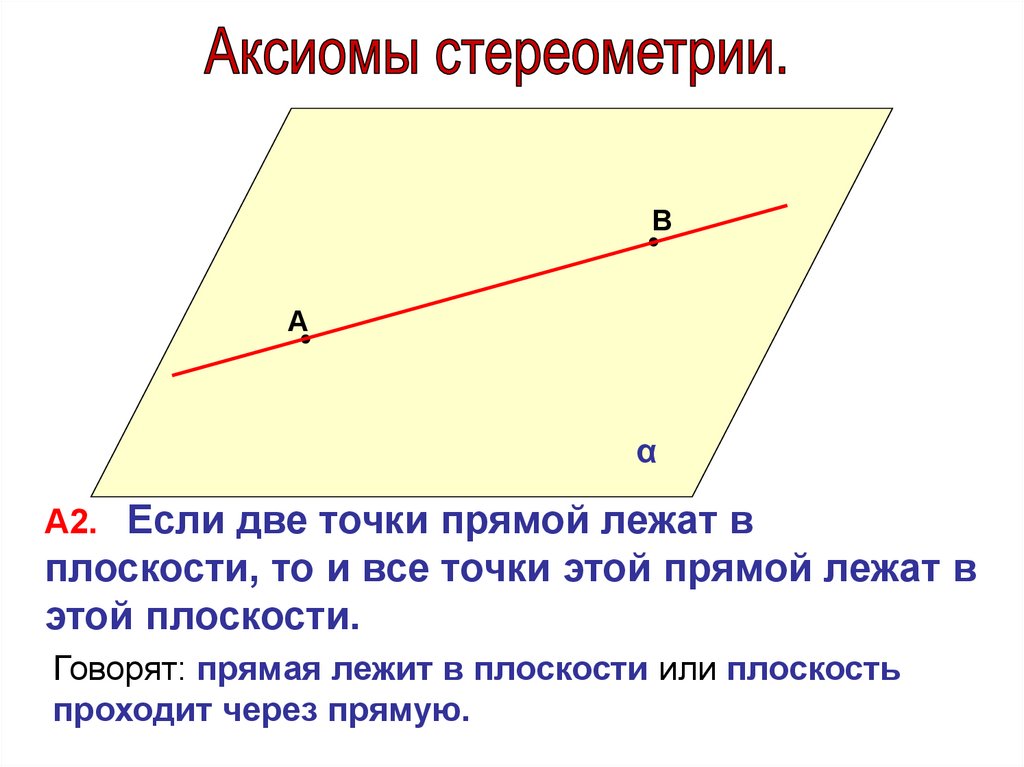
А2. Если две точки прямой лежат в
плоскости, то и все точки этой прямой лежат в
этой плоскости.
Говорят: прямая лежит в плоскости или плоскость
проходит через прямую.
11.
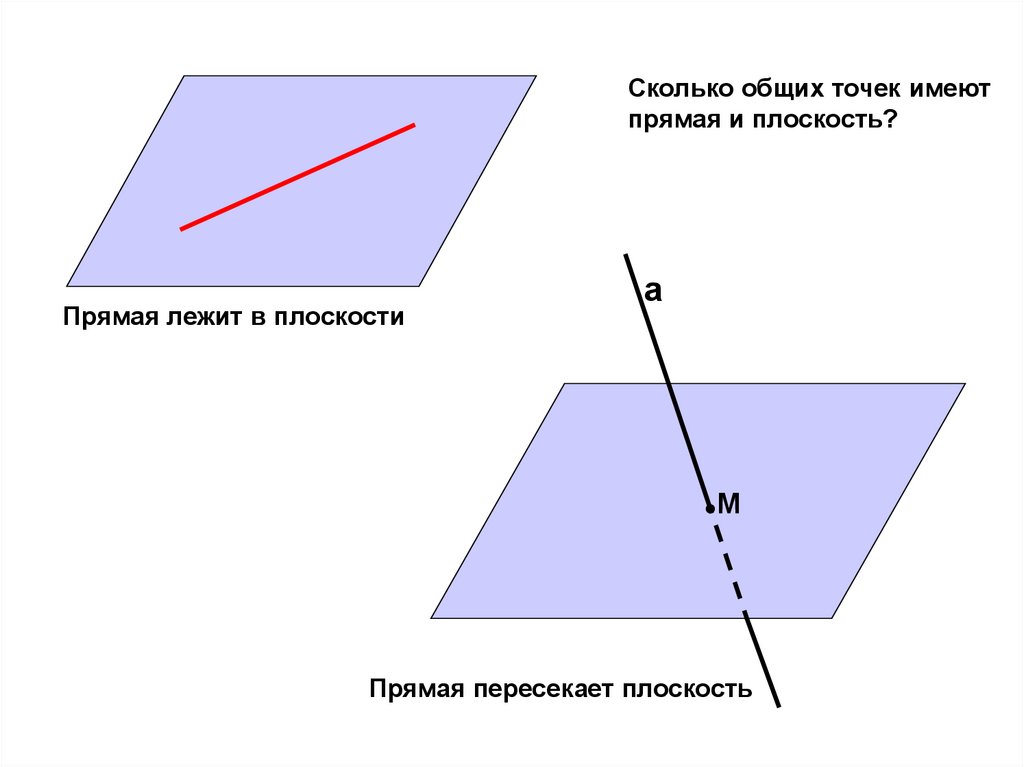
Сколько общих точек имеютпрямая и плоскость?
Прямая лежит в плоскости
а
М
Прямая пересекает плоскость
12.
βА
α
а
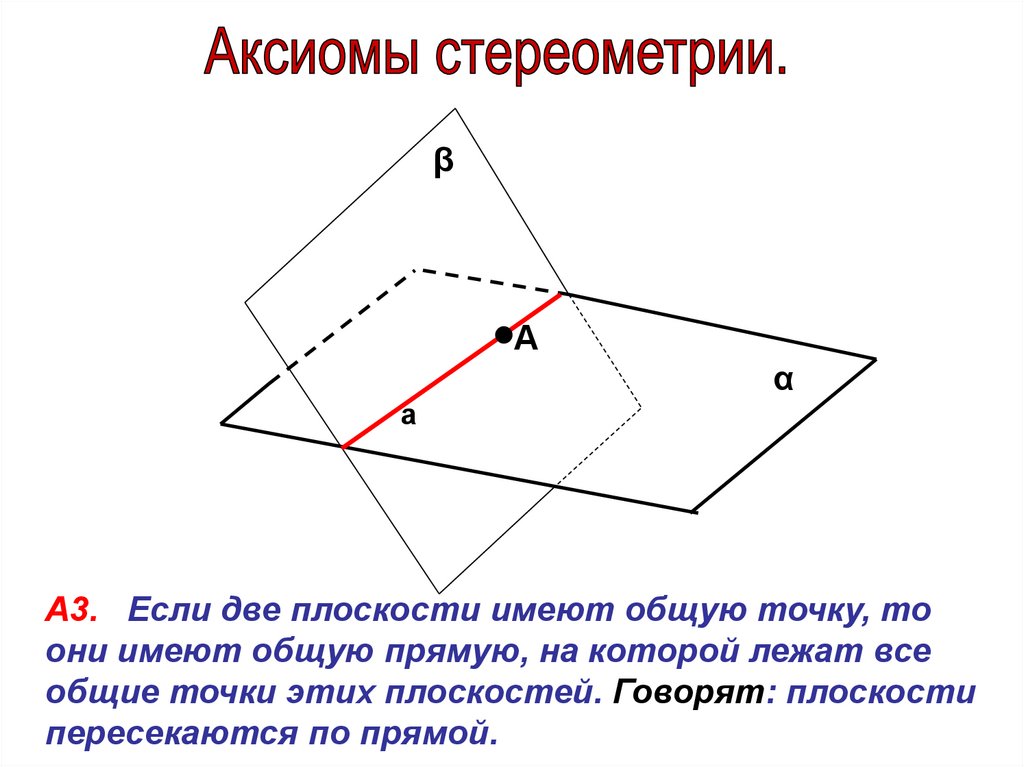
А3. Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат все
общие точки этих плоскостей. Говорят: плоскости
пересекаются по прямой.
13.
Решить задачи: №1(а,б); 2(а)Назовите по рисунку:
№1(а,б)
№ 2(а)
Д
В1
С1
Q
P
А1
Д1
К
К
М
Р
А
М
В
С
С
Е
В
а) плоскости, в которых лежат
прямые ДВ, АВ, МК, РЕ, ЕС; б) точки
пересечения прямой ДК с плоскостью
АВС, прямой СЕ с плоскостью АДВ.
А
Д
а) точки, лежащие в плоскостях
ДСС1 и ВQС
R
14.
15.
Некоторые следствия из аксиом:Теорема 1. Через прямую и не лежащую на ней точку
проходит плоскость и притом только одна.
Дано:
α
О
Доказать:
(а, М) с α
α- единственная
Р
а
а, М ¢ а
М
Доказательство :
1. Р, О с а; {Р,О,М} ¢ а
По аксиоме А1: через точки Р, О, М проходит плоскость .
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и
вся прямая принадлежит этой плоскости, т.е. (а, М) с α
2. Любая плоскость проходящая через прямую а и точку М
проходит через точки Р, О, и М, значит по аксиоме А1 она –
единственная. Ч.т.д.
16.
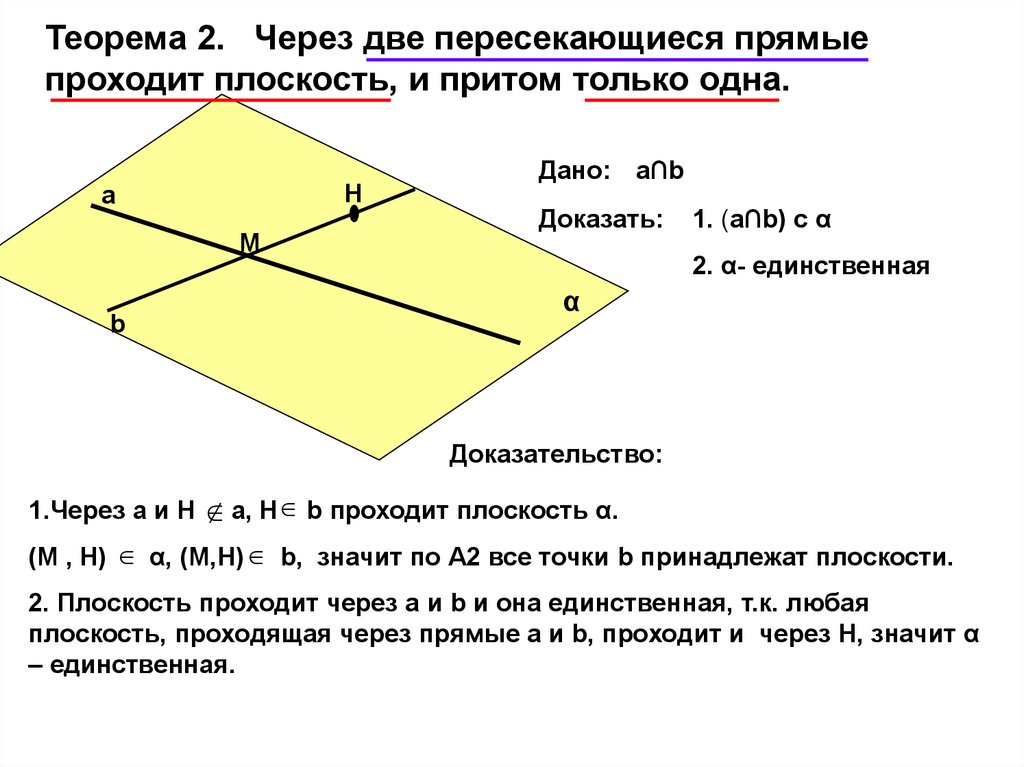
Теорема 2. Через две пересекающиеся прямыепроходит плоскость, и притом только одна.
Н
а
М
b
Дано: а∩b
Доказать:
1. (а∩b) с α
2. α- единственная
α
Доказательство:
1.Через а и Н
а, Н b проходит плоскость α.
(М , Н) α, (М,Н) b, значит по А2 все точки b принадлежат плоскости.
2. Плоскость проходит через а и b и она единственная, т.к. любая
плоскость, проходящая через прямые а и b, проходит и через Н, значит α
– единственная.
17.
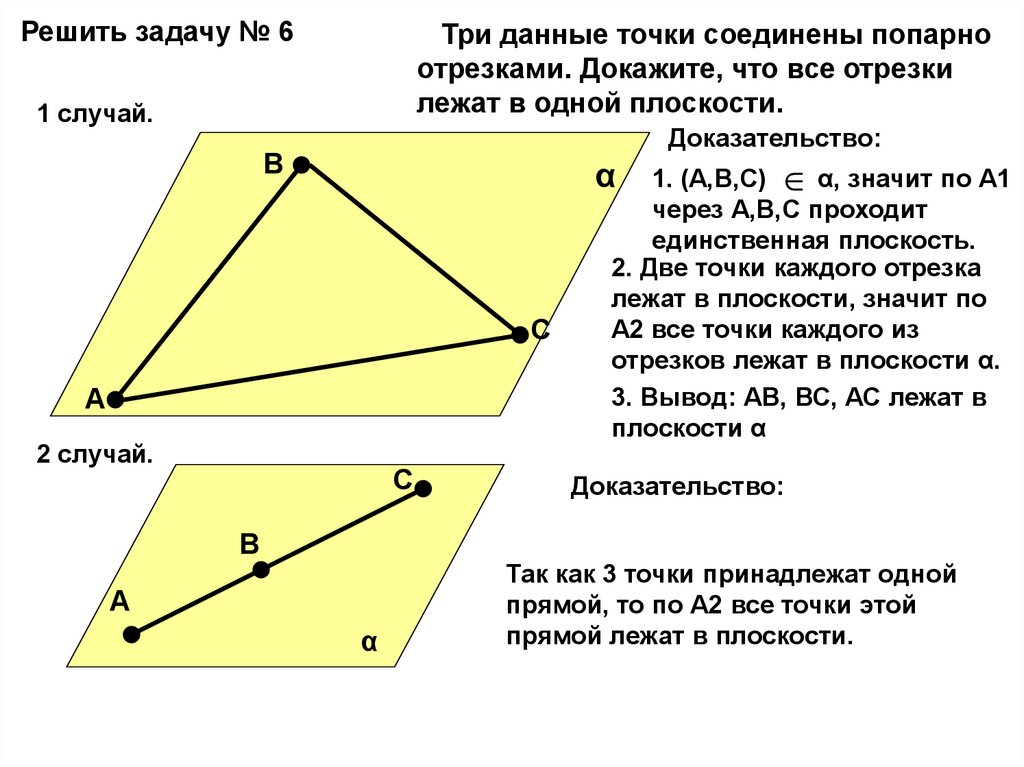
Решить задачу № 6Три данные точки соединены попарно
отрезками. Докажите, что все отрезки
лежат в одной плоскости.
1 случай.
Доказательство:
В
1. (А,В,С) α, значит по А1
через А,В,С проходит
единственная плоскость.
2. Две точки каждого отрезка
лежат в плоскости, значит по
А2 все точки каждого из
отрезков лежат в плоскости α.
3. Вывод: АВ, ВС, АС лежат в
плоскости α
α
С
А
2 случай.
С
В
А
α
Доказательство:
Так как 3 точки принадлежат одной
прямой, то по А2 все точки этой
прямой лежат в плоскости.
18.
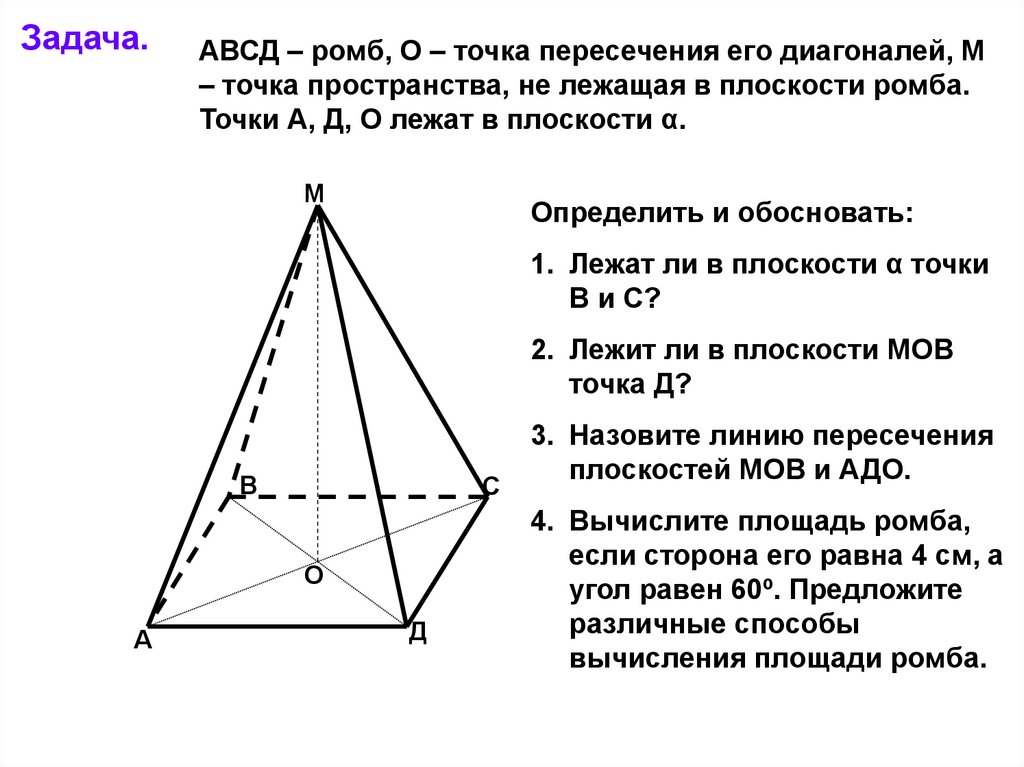
Задача.АВСД – ромб, О – точка пересечения его диагоналей, М
– точка пространства, не лежащая в плоскости ромба.
Точки А, Д, О лежат в плоскости α.
М
Определить и обосновать:
1. Лежат ли в плоскости α точки
В и С?
2. Лежит ли в плоскости МОВ
точка Д?
В
С
О
А
Д
3. Назовите линию пересечения
плоскостей МОВ и АДО.
4. Вычислите площадь ромба,
если сторона его равна 4 см, а
угол равен 60º. Предложите
различные способы
вычисления площади ромба.
19.
4В
С
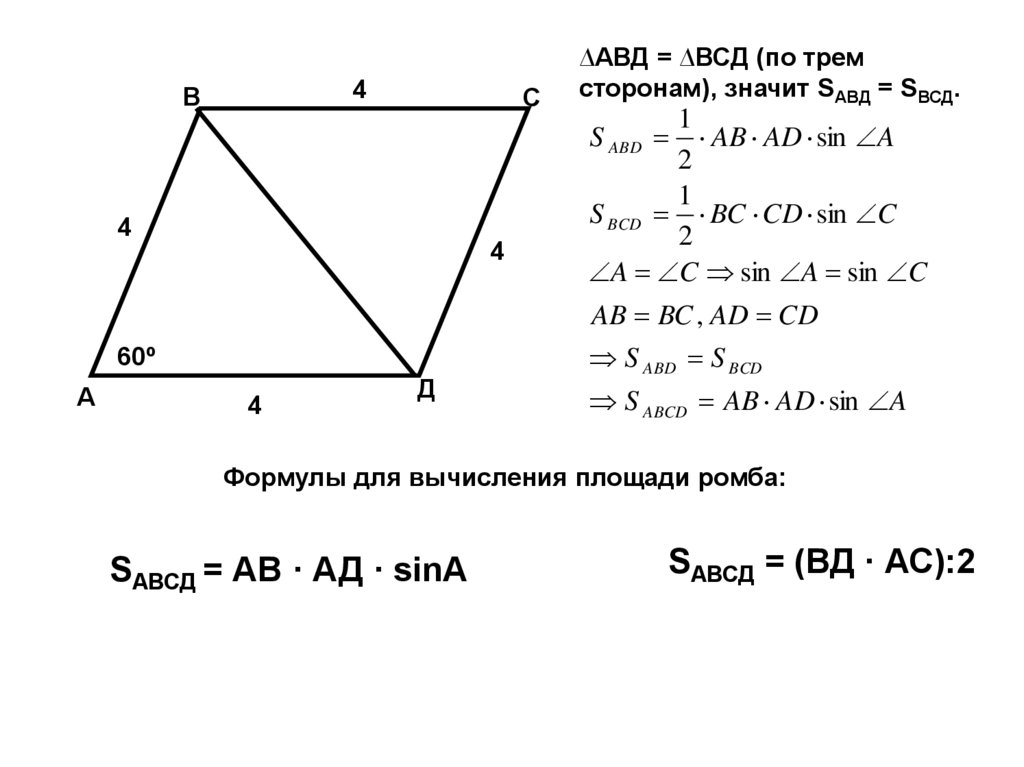
∆АВД = ∆ВСД (по трем
сторонам), значит SАВД = SВСД.
1
AB AD sin A
2
1
S BCD BC CD sin C
2
A C sin A sin C
S ABD
4
4
AB BC , AD CD
60º
А
4
Д
S ABD S BCD
S ABCD AB AD sin A
Формулы для вычисления площади ромба:
SАВСД = АВ · АД · sinA
SАВСД = (ВД · АС):2
20.
21.
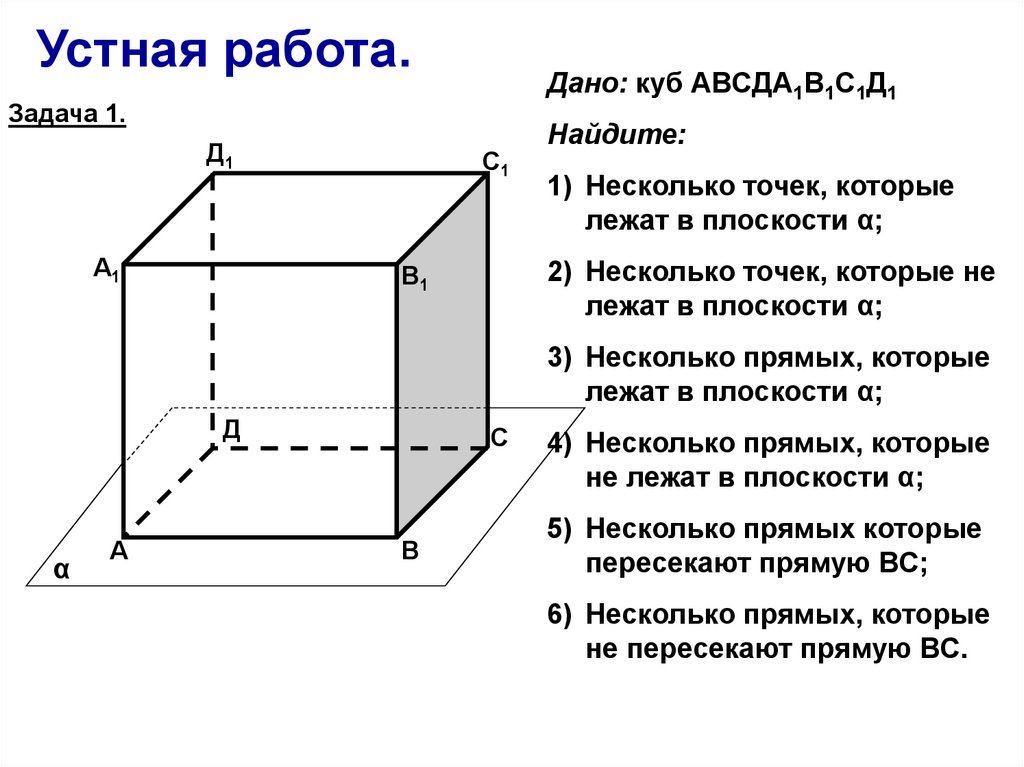
Устная работа.Дано: куб АВСДА1В1С1Д1
Задача 1.
Д1
А1
С1
Найдите:
1) Несколько точек, которые
лежат в плоскости α;
2) Несколько точек, которые не
лежат в плоскости α;
В1
3) Несколько прямых, которые
лежат в плоскости α;
Д
α
А
С
В
4) Несколько прямых, которые
не лежат в плоскости α;
5) Несколько прямых которые
пересекают прямую ВС;
6) Несколько прямых, которые
не пересекают прямую ВС.
22.
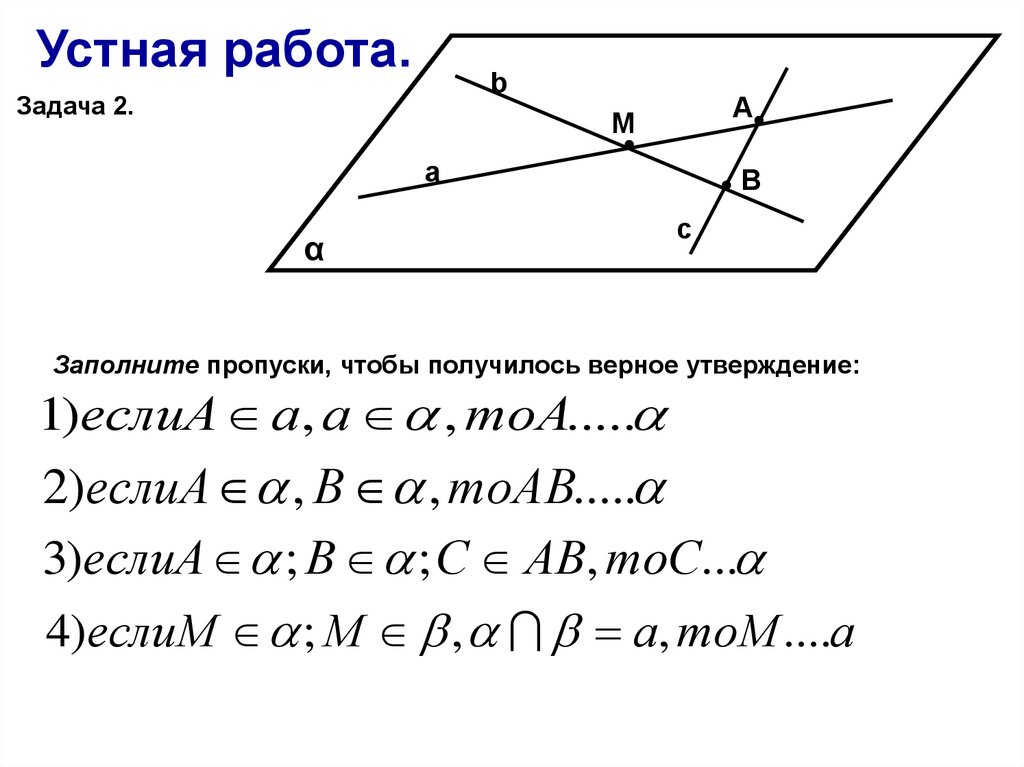
Устная работа.b
Задача 2.
А
М
а
α
В
c
Заполните пропуски, чтобы получилось верное утверждение:
1)еслиА а, а , тоА.....
2)еслиА , В , тоАВ.....
3)еслиА ; В ; С АВ, тоС...
4)еслиМ ; М , а, тоМ ....а
23.
Устная работа.Д1
А1
С1
В1
Д
α
А
Лежат ли прямые АА1,
АВ, АД в одной
плоскости?
С
В
Прямые АА1, АВ, АД
проходят через точку А,
но не лежат в одной
плоскости
24.
Дано: куб АВСДА1В1С1Д1Задача 1
т.М лежит на ребре ВВ1, т.N лежит на
ребре СС1 и точка К лежит на ребре ДД1
В1
С1
М
А1
Д1
а) назовите плоскости, в
которых лежат точки М; N.
б) найдите т.F-точку пересечения
прямых МN и ВС. Каким свойством
обладает точка F?
в) найдите точку пересечения
прямой КN и плоскости АВС
г) найдите линию пересечения
плоскостей МNК и АВС
N
В
С
К
Д
А
О
F
25.
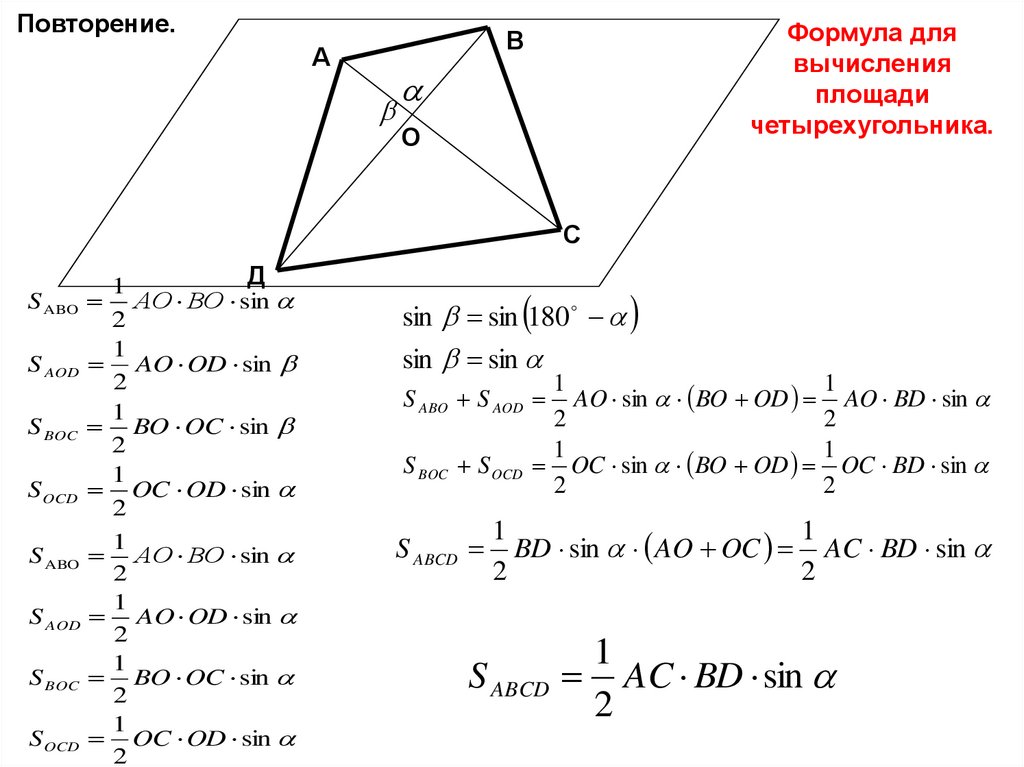
Повторение.Формула для
вычисления
площади
четырехугольника.
В
А
О
С
Д
1
S ABO АО ВО sin
2
1
S AOD AO OD sin
2
1
S BOC BO OC sin
2
1
S OCD OC OD sin
2
1
S ABO АО ВО sin
2
1
S AOD AO OD sin
2
1
S BOC BO OC sin
2
1
S OCD OC OD sin
2
sin sin 180
sin sin
1
1
AO sin BO OD AO BD sin
2
2
1
1
OC sin BO OD OC BD sin
2
2
S ABO S AOD
S BOC S OCD
S ABCD
1
1
BD sin AO OC AC BD sin
2
2
S ABCD
1
AC BD sin
2
26.
Задача 2Докажите, что все вершины
четырехугольника АВСД лежат в
одной плоскости, если его
диагонали АС и ВД пересекаются.
В
А
О
Вычислите площадь
четырехугольника, если АС┴ВД,
АС = 10см, ВД = 12см.
С
Д
α
Доказательство:
1. (АС ∩ ВД) =α АС
α, ВД α,
(А, В, С, Д )
2. SАВСД = АС · ВД · sin90º = 10 · 12 = 120 (см2)
Ответ: 120 см2
α
27.
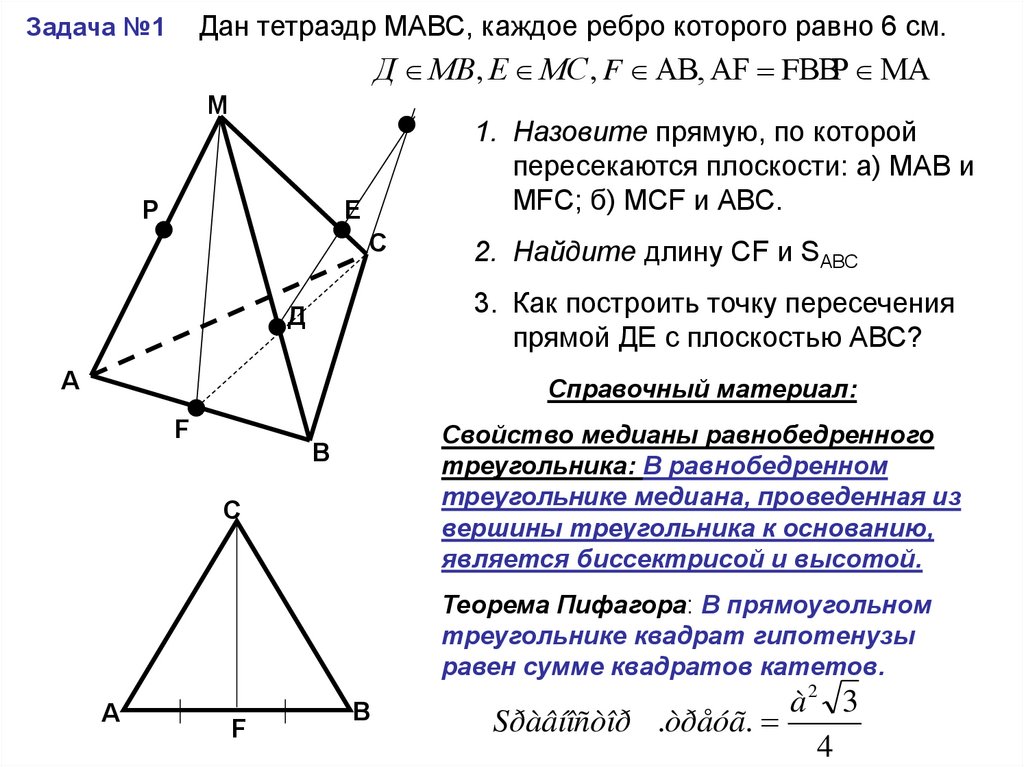
Дан тетраэдр МАВС, каждое ребро которого равно 6 см.Задача №1
Д МВ, Е МС , F АВ, АF FВВР МА
М
Р
1. Назовите прямую, по которой
пересекаются плоскости: а) МАВ и
МFС; б) МСF и АВС.
Е
С
2. Найдите длину СF и SАВС
3. Как построить точку пересечения
прямой ДЕ с плоскостью АВС?
Д
А
Справочный материал:
F
Свойство медианы равнобедренного
треугольника: В равнобедренном
треугольнике медиана, проведенная из
вершины треугольника к основанию,
является биссектрисой и высотой.
В
С
Теорема Пифагора: В прямоугольном
треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
А
F
В
à2 3
Sðàâíîñòîð .òðåóã.
4
28.
Задача №2Дано : АВСДА1В1С1 Д1 куб , Р ВВ1, В1Р РВ.
Д1
А1
С1
В1
2) Как построить линию
пересечения плоскости
АД1Р и АВВ1?
Р
3) Вычислите длину
отрезков АР и АД1, если
АВ = а
Д
А
1) Как построить точку
пересечения плоскости
АВС с прямой Д1Р?
С
В
К
29.
Задача №3А
М
Р
К
В
α
С
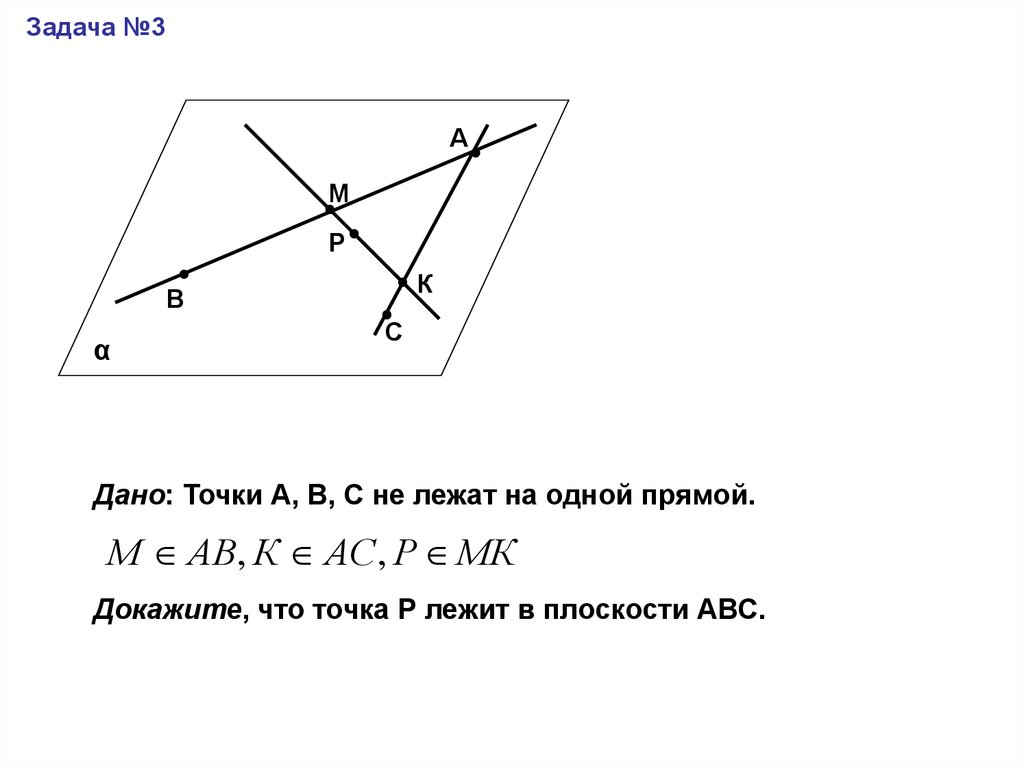
Дано: Точки А, В, С не лежат на одной прямой.
М АВ, К АС, Р МК
Докажите, что точка Р лежит в плоскости АВС.
30.
Задача(устно)
АВСД – ромб, О – точка пересечения его диагоналей, М –
точка пространства, не лежащая в плоскости ромба. Точки
А, Д, О лежат в плоскости α.
Определить и обосновать:
1. Какие еще точки лежат в
плоскости α?
М
1. Лежат ли в плоскости α точки В и
М?
2. Лежит ли в плоскости МОД точка
В?
3. Назовите линию пересечения
плоскостей МОС и АДО.
С
В
О
А
Д
4. Точка О – общая точка
плоскостей МОВ и МОС. Верно
ли что эти плоскости
пересекаются по прямой МО?
5. Назовите три прямые, лежащие
в одной плоскости; не лежащие в
одной плоскости.
31.
ЗадачаСтороны АВ и АС треугольника АВС
лежат в плоскости . Докажите, что
и медиана лежит в плоскости .
(устно)
В
М
А
С
32.
Задача(устно)
В чем ошибка чертежа, где О ЕF. Дайте
объяснение. Как должен выглядеть правильный
чертеж.
М
Е
F
О
В
С
Д
33.
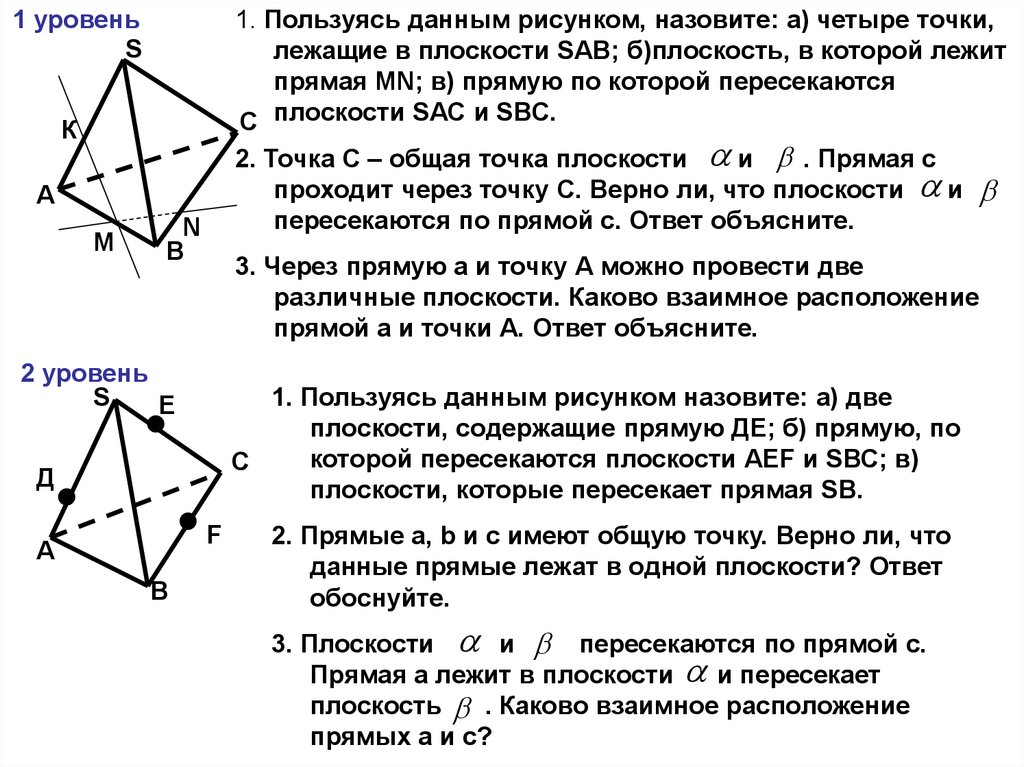
1 уровеньS
1. Пользуясь данным рисунком, назовите: а) четыре точки,
лежащие в плоскости SАВ; б)плоскость, в которой лежит
прямая МN; в) прямую по которой пересекаются
С плоскости SАС и SВС.
К
2. Точка С – общая точка плоскости и . Прямая с
проходит через точку С. Верно ли, что плоскости и
пересекаются по прямой с. Ответ объясните.
А
М
N
В
3. Через прямую а и точку А можно провести две
различные плоскости. Каково взаимное расположение
прямой а и точки А. Ответ объясните.
2 уровень
S
Е
1. Пользуясь данным рисунком назовите: а) две
плоскости, содержащие прямую ДЕ; б) прямую, по
которой пересекаются плоскости АЕF и SВС; в)
С
плоскости, которые пересекает прямая SВ.
Д
F
А
В
2. Прямые а, b и с имеют общую точку. Верно ли, что
данные прямые лежат в одной плоскости? Ответ
обоснуйте.
3. Плоскости и пересекаются по прямой с.
Прямая а лежит в плоскости и пересекает
плоскость . Каково взаимное расположение
прямых а и с?
34.
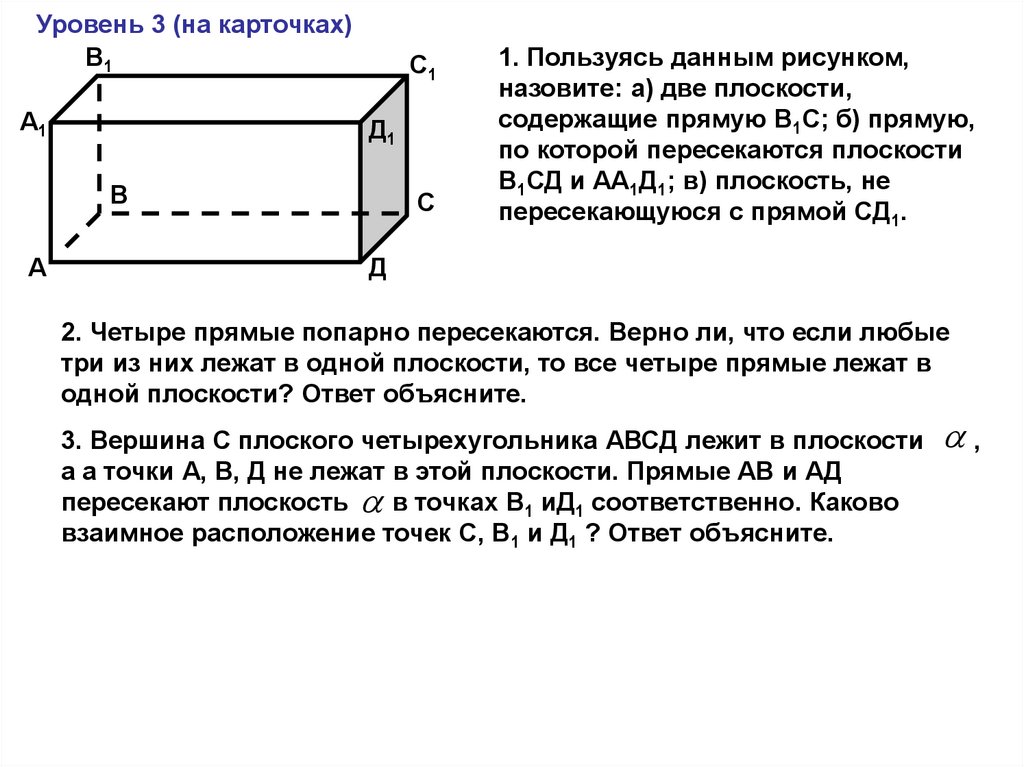
Уровень 3 (на карточках)В1
А1
С1
Д1
В
А
С
1. Пользуясь данным рисунком,
назовите: а) две плоскости,
содержащие прямую В1С; б) прямую,
по которой пересекаются плоскости
В1СД и АА1Д1; в) плоскость, не
пересекающуюся с прямой СД1.
Д
2. Четыре прямые попарно пересекаются. Верно ли, что если любые
три из них лежат в одной плоскости, то все четыре прямые лежат в
одной плоскости? Ответ объясните.
3. Вершина С плоского четырехугольника АВСД лежит в плоскости
а а точки А, В, Д не лежат в этой плоскости. Прямые АВ и АД
пересекают плоскость в точках В1 иД1 соответственно. Каково
взаимное расположение точек С, В1 и Д1 ? Ответ объясните.
,
35.
Домашнее задание:- выучить аксиомы стереометрии, выполнить задания
выбранного уровня
-повторить материал из планиметрии и сделать в
тетрадях конспект по следующим вопросам:
1. Определение параллельных прямых
2. Взаимное расположение двух прямых на плоскости
3. Построение прямой, параллельной данной
4. Аксиому о параллельных прямых.


















 Математика
Математика








