Кристаллография и основы кристаллохимии

1.

2.

Теорема 1. Линия пересечения двух плоскостей симметрии всегда является осью
симметрии, действие которой равно сумме действий обеих плоскостей; элементарный угол
поворота оси вдвое больше угла, образованного плоскостями.
Предыдущую теорему можно сформулировать и в следующем более общем виде:
действие двух пересекающихся зеркальных плоскостей равносильно действию одной
поворотной оси, лежащей на линии пересечения упомянутых плоскостей, причем угол
поворота оси вдвое больше угла, заключенного между плоскостями.
Тем самым два отражения в двух пересекающихся плоскостях заменяются без
изменения результатов одним поворотом вокруг оси.

3.

Существует также и обратная теорема: действие одной поворотной оси
равносильно действию двух зеркальных плоскостей, пересекающихся вдоль упомянутой
оси. При этом первая зеркальная плоскость проводится вдоль оси произвольно, а вторая
плоскость должна образовывать (в направлении поворота оси) с первой плоскостью угол,
равный половине элементарного угла поворотной оси.
Таким образом, один поворот вокруг оси заменяется без изменения результатов
двумя отражениями в двух плоскостях.

4.

Теорема 2. При наличии двух пересекающихся осей симметрии всегда следует
искать третью равнодействующую ось, проходящую через точку пересечения первых двух
(теорема Эйлера).
Теорема 3. При наличии центра симметрии С и четной оси L2n перпендикулярно
последней проходит плоскость симметрии Р.
При наличии центра симметрии С и проходящей через него плоскости симметрии
Р перпендикулярно последней находится четная ось симметрии L2n.
При наличии четной оси L2n и перпендикулярной к ней плоскости симметрии Р
всегда присутствует центр симметрии С.
L2n×С = L2nPС;
L2n×P = L2nPС;
P×С = L2nPС

5.

Важное значение для нахождения элементов симметрии имеет следствие из
предыдущей теоремы.
Следствие из теоремы 3. При наличии центра симметрии сумма четных осей
равна сумме плоскостей симметрии, причем каждая четная ось перпендикулярна
плоскости симметрии.
L4РС
L33L23РС
L66L27РС
3L44L36L29РС

6.

Теорема 4. В присутствии оси симметрии n-ого порядка (Ln) и перпендикулярной
к ней оси второго порядка L2 имеем всего n таких осей (nL2).
Ln×L2 = LnnL2
Теорема 5. В присутствии оси симметрии n-ого порядка (Ln) и плоскости
симметрии Р, проходящей вдоль этой оси, имеем всего n таких плоскостей (nР).
Ln×Р = LnnP

7.

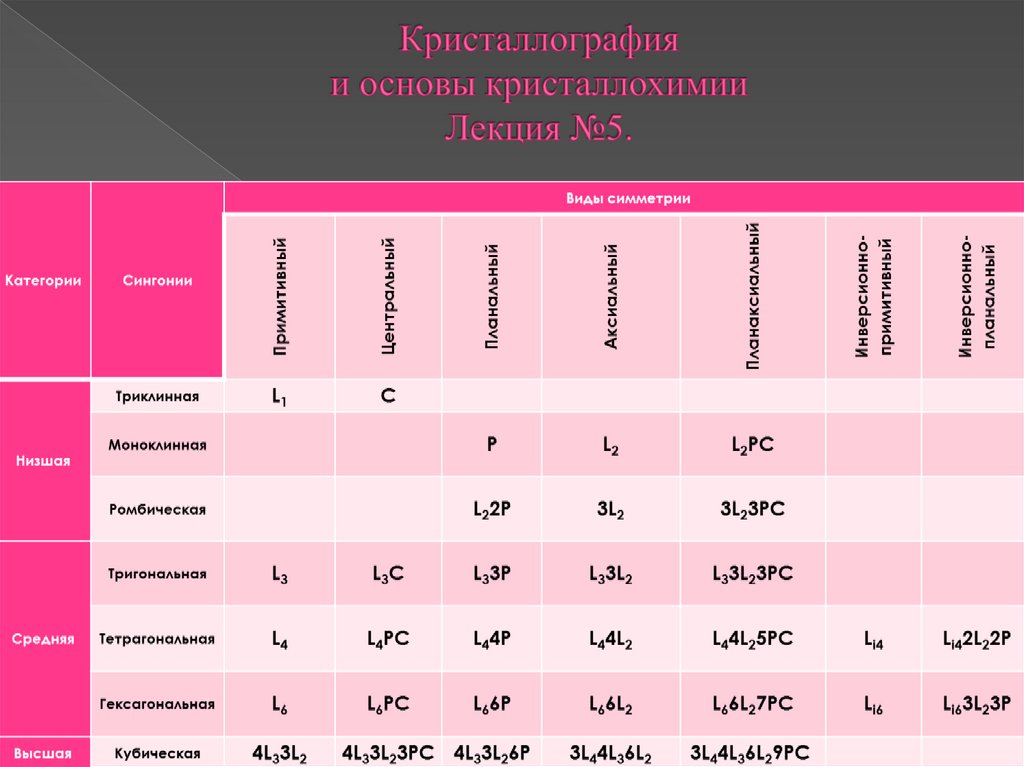
Видом симметрии кристаллического
совокупность его элементов симметрии.
многогранника
называется
полная
В кристаллографии насчитывается 32 вида симметрии.
1. Единичное направление совпадает с единственной осью симметрии Ln.
Отсюда выводим четыре вида симметрии: L1, L3, L4 и L6. Полученные виды
симметрии, каждый из которых состоит только из одной оси симметрии, носят название
примитивных.

8.

2. К исходному единичному направлению, прибавляется центр симметрии С.
Согласно вышеуказанному, единичное направление может совпадать с той или
иной осью симметрии. Поэтому, перебирая все возможные случаи, получаем: L1C, L3C,
L4C и L6C. Вспоминаем теорему, согласно которой при наличии четной оси и центра
симметрии появляется плоскость симметрии, перпендикулярная оси.
L1×С=С;
L3×С=L3С;
L4×С=L4РС;
L6×С=L6РС
Найденные виды симметрии называются центральными.

9.

3. К исходному единичному направлению прибавляется плоскость симметрии Р,
идущая вдоль него.
Единичное направление может совпадать с одной из возможных осей симметрии.
Чтобы исчерпать все мыслимые случаи, прибавляем к таким осям проходящие вдоль них
плоскости симметрии. Вспоминаем теорему, согласно которой, при наличии Ln и
плоскости, лежащей вдоль нее, имеем всего n таких плоскостей.
L1×Р=Р;
L2×Р=L22Р;
L3×Р=L33Р;
L4×Р=L44Р;
L6×Р=L66Р
Пять новых видов, симметрии называются планальными.

10.

4. Перпендикулярно исходному единичному направлению присоединяется ось
симметрии L2.
К возможным осям симметрии, совпадающим с единичным направлением,
прибавляем оси симметрии L2. Согласно теореме при наличии Ln и перпендикулярной к ей
L2 имеем всего nL2.
L1×L2= L1L2=L2;
L2×L2= L22L2=3L2;
L3×L2=L33L2;
L4×L2=L44L2;
L6×L2=L66L2
Пять новых видов симметрии носят название аксиальных.

11.

5. К исходному единичному направлению присоединяем все возможные
сочетания элементов симметрии.
L1×С×Р×L2=L2РС;
L2×С×Р×L2=3L23РС;
L3×С×Р×L2=L33L23РС;
L4×С×Р×L2=L44L25РС;
L6×С×Р×L2=L66L27РС
Полученные пять новых видов симметрии называются планаксиальными.

12.

6. Единичное направление совмещено с единственной инверсионной осью Lin.
Выделяют: инверсионно-примитивный вид симметрии, к которому относятся
кристаллы с формулами
Li4
Li6
инверсионно-планальный вид симметрии, к которому относятся кристаллы с
формулами
Li42L22P (3L22P)
Li63L23P (L33L24P)
В результате для кристаллов с единичными направлениями насчитываем
всего 27 видов симметрии.

13.

Перейдем к тем случаям, когда в кристаллах нет единичных направлений. Из
каждого направления выводятся симметрично-равные ему. Тем самым, и любые оси
симметрий повторяются несколько раз. Математически доказано, что совокупности осей
симметрии отвечают здесь таким комбинациям, которые наблюдаются на правильных
многогранниках, известных из геометрии.
Для высшей категории кубической сингонии:
4L33L2 примитивный вид симметрии;
4L33L23РС центральный вид симметрии;
4L33L26Р планальный вид симметрии;
3L44L36L2 аксиальный вид симметрии;
3L44L36L29РС планаксиальный вид симметрии.
В результате вывода получено всего 32 вида симметрии или 32 совокупности
элементов симметрии, возможных для кристаллических многогранников.