Кристаллография (лекция 1)

1.

Кристаллография
Лекция №1
Тема 1. Введение
Тема 2. Понятия о симметричном объекте, симметрическом
преобразовании и элементах симметрии
Тема 3. Элементы симметрии I рода
Тема 4. Элементы симметрии II рода

2.

Кристаллография
Лекция №1
Курс «Кристаллография» – 4 з.е. (144 часа). Из них:
- 28 ч. лекции;
- 32 ч. практические занятия;
- 84 ч. самостоятельная работа студента, из которых:
- 36 ч. подготовка к экзамену;
- 48 ч. самостоятельная работа в семестре.
2

3.

Кристаллография
Лекция №1
Учебно-методическое обеспечение:
а) Электронный учебный курс по дисциплине в электронном
университете «Moodle» – https://moodle.tsu.ru/course/view.php?id=2147
б) Оценочные материалы текущего контроля и промежуточной
аттестации по дисциплине: список экзаменационных вопросов; тестовые
задания и контрольные работы, с которыми работают обучающиеся на
практических занятиях
в) Князев Г.Б. Минералогическая кристаллография: учебнометодический комплекс / Г.Б. Князев, С.Д. Гармаева, А.А. Баева. – Томск:
ИДО
ТГУ,
2010.
–
http://vital.lib.tsu.ru/vital/access/manager/Repository/vtls:000405248
г) Для работы на практических занятиях и самостоятельной работы
используется учебная коллекция идеальных моделей кристаллов (50 шт.).
3

4.

Кристаллография
Лекция №1
Основная литература
Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия. –
М.: Книжный дом "Университет", 2010. – 587 с.
Дополнительная литература
1. Князев Г.Б. Введение в кристаллографию. – Томск: ТГУ, 2000. – 178 с.
2. Нардов В.В. Практическое руководство по геометрической кристаллографии.
– Л.: Изд-во ЛГУ, 1974. – 142 с.
3. Попов Г.М., Шафрановский И.И. Кристаллография. – М.: Высшая школа, 1964.
– 371 c.
4

5.

Кристаллография
Лекция №1
Кристаллография – одна из главных фундаментальных наук о
Земле и ее веществе. Это наука о кристаллах, о процессах их
образования, об их внешней форме, внутреннем строении и физических
свойствах.
Своим зарождением кристаллография обязана наблюдению и
изучению природных объектов: минералов и сложенных ими горных
пород. Долгое время кристаллография была частью минералогии. Однако
впоследствии кристаллография выделилась в самостоятельную область
знаний.
5

6.

Кристаллография
Лекция №1
Кристаллография обладает уникальным, только ей присущим
методом – это метод симметрии, который является общим методом
познания закономерностей развития Земли и ее вещества.
Таким образом, симметрия является главным свойством всякого
кристалла. Применение законов симметрии составляет основу всех
кристаллографических
методов,
что
и
делает
кристаллографию
самостоятельной наукой.
6

7.

Кристаллография
Лекция №1
Термин «симметрия» ввел в обиход
Пифагор
(VI
в.
до
пространственную
расположении
н.э.),
обозначив
им
закономерность
в
одинаковых
фигур
или
их
отклонение
от
частей.
Он
же
определил
симметрии как асимметрию.
Теоретической
разработкой
учения
о
симметрии до последнего времени занимались
исключительно математики и кристаллографы.
7

8.

Кристаллография
Лекция №1
Слово «симметрия» употребляется в двух
значениях:
1) нечто, обладающее хорошими пропорциями
(синоним
«гармония»)
–
используется
в
музыке, танце, архитектуре, поэзии и т. д.;
2) двусторонняя, т.е. зеркальная симметрия. Это
уже
строго
геометрическое
понятие.
Пространственный образ (тело) может быть
симметричен
относительно
либо
данной
плоскости, либо прямой линии.
8

9.

Кристаллография
Лекция №1
Рябь на песке
Двустворчатые
моллюски с
плоскостью
симметрии
Рябь на
песчанике
Брюхоногие
моллюски без
плоскости
симметрии
9

10.

Кристаллография
Лекция №1
Формы складок в поперечном
разрезе:
а – симметричные;
б – асимметричные
Схема срединно-океанического
хребта, через который проходит
зеркальная
плоскость симметрии (Р)
10

11.

Кристаллография
Лекция №1
Симметричным объект можно назвать лишь в том случае, если
он может быть совмещен сам с собой поворотами или (и) отражениями.
Если в результате таких преобразований объект (или его части)
совместится сам с собой, то он является симметричным, а
преобразование, с помощью которого достигнуто это совмещение,
называется симметрическим преобразованием. Суть симметрии
заключается в возможности произвести преобразование объекта,
совмещающее его с самим собой в новом положении.
Геометрические образы (плоскости, прямые линии или точки), с
помощью которых задаются или осуществляются симметрические
преобразования (операции), называются элементами симметрии.
11

12.

Кристаллография
Лекция №1
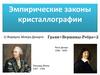
В зависимости от характера преобразования различают элементы
симметрии I и II рода.
Элементы симметрии I рода связывают друг с другом
конгруэнтно равные фигуры (или их части), т.е. фигуры, совмещающиеся
при наложении: правые – с правыми, левые – с левыми.
Элементы симметрии II рода связывают друг с другом
энантиоморфные, т.е. зеркально равные, фигуры или их части – правые с
левыми.
12

13.

Кристаллография
Лекция №1
Элементами симметрии I рода являются поворотные оси симметрии –
прямые, при повороте вокруг которых на определенный угол фигура (или
кристалл) совмещается сама с собой.
Наименьший угол поворота вокруг такой оси, приводящий фигуру к
самосовмещению, называется элементарным углом поворота оси симметрии и
обозначается как α.
Величина угла поворота определяет порядок оси симметрии – n,
равный числу самосовмещений при полном повороте на 360°.
Зависимость величины угла поворота и порядка оси симметрии:
n = 360°:α
13

14.

Кристаллография
Лекция №1
В учебной символике – символике Браве – оси
симметрии обозначаются
Ln
подстрочный цифровой индекс n указывает на
порядок оси. Графически оси симметрии обозначаются
многоугольниками. Ось 1-го порядка L1, графического
значка не имеет и в кристаллах не определяется.
В геометрических фигурах возможны оси симметрии
любого порядка.
В кристаллических многогранниках порядок осей
ограничен числами n = 1, 2, 3, 4, 6, т.е. в кристаллах
невозможны оси 5-го и выше 6-го порядков. В этом суть
основного закона симметрии кристаллов, подтвержденного
внутренним строением кристаллов.
14

15.

Кристаллография
Лекция №1
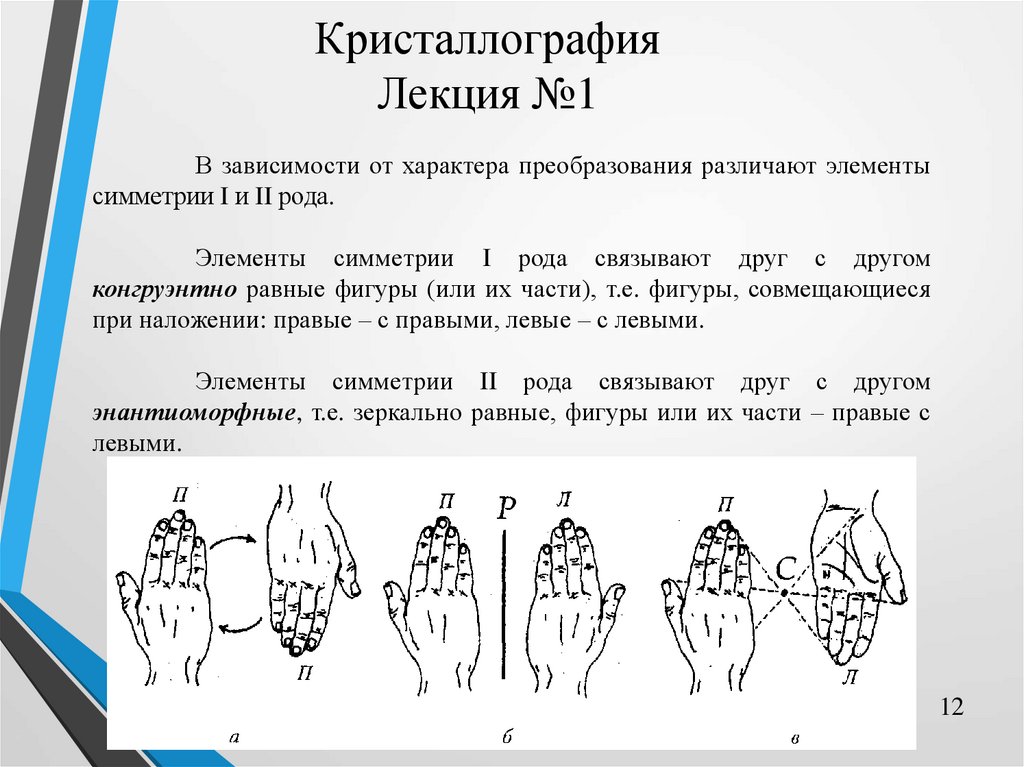
В геометрических фигурах возможны оси симметрии любого
порядка.
Закон
симметрии
кристаллов:
в
кристаллических
многогранниках порядок осей ограничен числами n = 1, 2, 3, 4, 6, т.е. в
кристаллах невозможны оси 5-го и выше 6-го порядков.
Это ограничение обусловлено тем, что кристаллическое
вещество – бесконечная система частиц, симметрично повторяющихся в
пространстве.
L2 (α=180°);
L3 (α=120°);
L4 (α=90°);
L6 (α=60°).
15

16.

Кристаллография
Лекция №1
16

17.

Кристаллография
Лекция №1
Оси 1-го и 2-го порядков принято называть осями низшего
порядка, оси выше 2-го порядка – осями высшего порядка.
Количество осей одного и того же порядка обозначается
коэффициентом перед символом оси симметрии. Например, 3L4
читается как три оси четвертого порядка.
Возможное количество осей одного и того же порядка:
L2 – 0, 1, 2, 3, 4, 6;
L3 – 0, 1, 4;
L4 – 0, 1, 3;
L6 – 0, 1.
Оси симметрии в кристалле могут выходить из:
- центра граней;
- середины ребер;
- из вершин.
17

18.

Кристаллография
Лекция №1
К элементам симметрии II рода относятся: плоскость симметрии, центр
инверсии, а также зеркально-поворотные и инверсионные оси.
Плоскость симметрии – плоскость, которая делит кристалл на две зеркально
равные части. В результате этот элемент симметрии связывает энантиоморфные фигуры, т.е.
какую-либо фигуру (или ее часть) с ее зеркальным отражением. В символике Браве
зеркальная плоскость симметрии (и операция отражения в плоскости) обозначается буквой
Р
Графически – двойной линией.
Плоскости симметрии проходят через середины граней и ребер перпендикулярно
им, или же идут вдоль ребер, образуя равные углы с одинаковыми гранями и ребрами.
В кристаллах возможно от 1 до 9 плоскостей, исключая 8.
18

19.

Кристаллография
Лекция №1
19

20.

Кристаллография
Лекция №1
Энантиоморфные фигуры могут быть связаны и другим элементом
симметрии – центром симметрии (центр инверсии), «зеркальной точкой»,
«отражаясь» в которой правая фигура не только переходит в левую, но и как бы
переворачивается.
Центр симметрии – точка внутри кристалла, в которой пересекаются
и делятся пополам линии, соединяющие противоположные одинаковые грани,
ребра или вершины кристалла.
Это особая точка внутри фигуры. Любая проведенная через центр
симметрии прямая по обе стороны от нее и на равных расстояниях встречает
соответственные точки фигуры.
20

21.

Кристаллография
Лекция №1
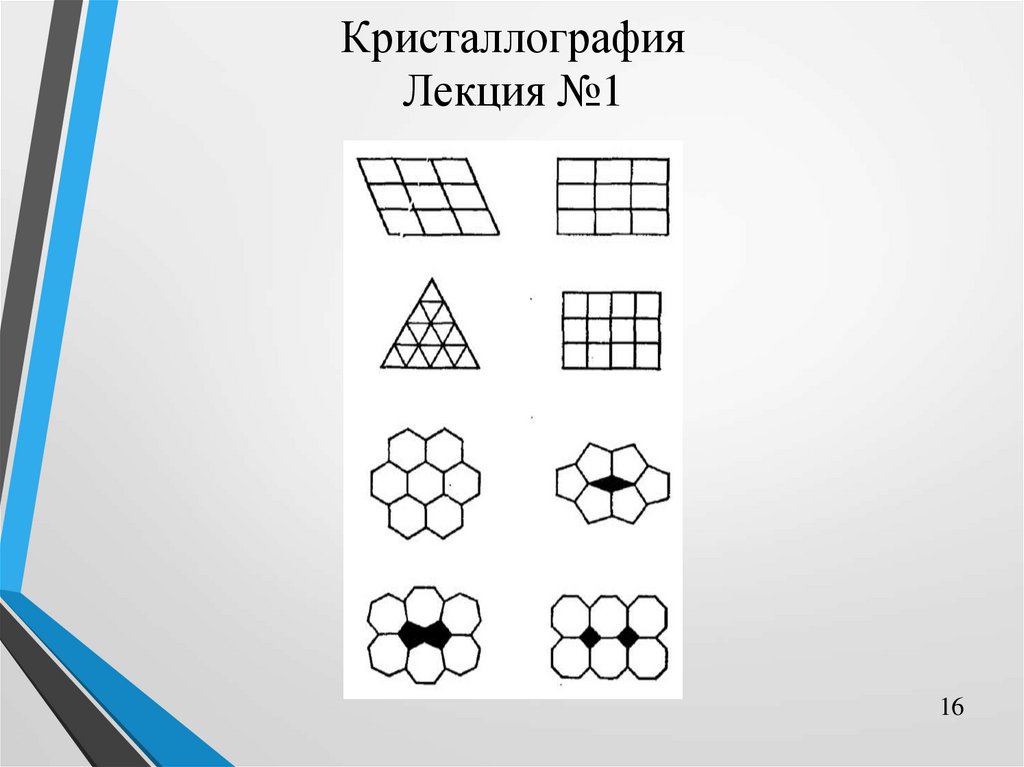
Правило наличия центра симметрии: если в кристалле
имеется центр симметрии, то каждая грань его должна иметь себе
равную и параллельную (обратно направленную) грань.
Обозначается центр инверсии в символике Браве буквой С,
графически также буквой С.
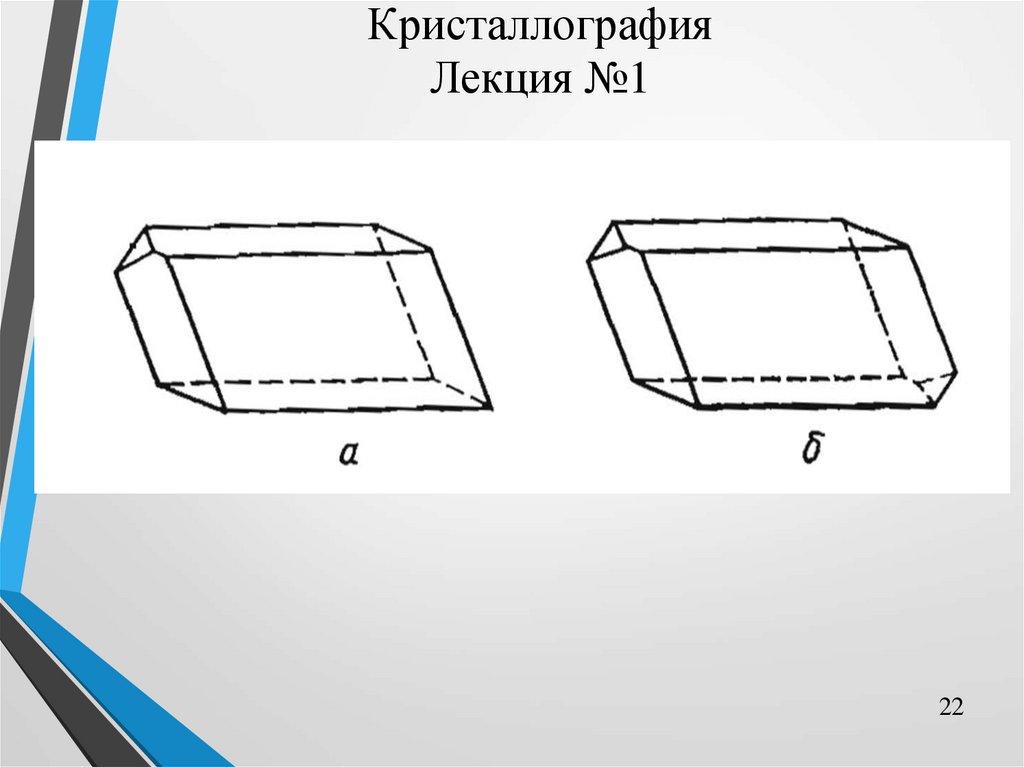
В параллелепипеде есть центр симметрии, любой грани
соответствует такая же равная и параллельная грань.
А в пирамидах никогда центра симметрии не будет, т.к. для
грани, являющейся основанием пирамиды, не найдется параллельная и
равная ей грань.
21

22.

Кристаллография
Лекция №1
22

23.

Кристаллография
Лекция №1
Рассмотренные элементы симметрии – поворотные оси,
зеркальная плоскость и центр инверсии – часто называют
простыми,
так
как
каждый
из
них
задает
лишь
одну
симметрическую операцию: поворот, отражение или инверсию в
точке соответственно.
Для описания же симметрии некоторых кристаллов простых
элементов симметрии оказывается явно недостаточно, так как в них
могут присутствовать сложные элементы симметрии, позволяющие
совмещать равные фигуры (или их части) путем двойной операции –
поворота (операции I рода) и отражения (операции II рода).
23

24.

Кристаллография
Лекция №1
Инверсионная ось симметрии –
прямая линия, при повороте вокруг которой
на некоторый определенный угол с
последующим
(или
предварительным)
отражением в центральной точке фигуры,
как в центре инверсии, фигура совмещается
со своим исходным положением.
Центр инверсии лишь составная часть инверсионной оси, поэтому в
кристаллах, имеющих инверсионные оси, отдельного центра инверсии нет.
Инверсионные оси представляют собой уже хорошо известные нам
элементы симметрии:
Li1 = C; Li2 = P;
Li3 = L3C; Li4 ՜ L2;
=
Li6 = L3┴P.
24

25.

Кристаллография
Лекция №1
Зеркально-поворотная
(или
просто
зеркальная)
ось
симметрии – прямая линия, при повороте вокруг которой на некоторый
определенный угол с последующим (или предварительным) отражением
в перпендикулярной к ней плоскости, фигура совмещается со своим
исходным положением.
В определении этих осей нет необходимости, если определяются
и используются инверсионные оси. Любая зеркально-поворотная ось
может быть заменена инверсионной.
25