Динамика. Лекция 8

1.

Динамика

2.

Лекция 8
Законы сохранения. Элементы теории
моментов инерции. Кинетический момент
твердого тела. Дифференциальное
уравнение вращения твердого тела. Пример
решения задачи на использование теоремы
об изменении момента количества движения
системы. Элементарная теория гироскопа.

3.

Элементы теории моментов инерции – При вращательном движении
твердого тела мерой инерции (сопротивления изменению движения)
является момент инерции относительно оси вращения. Рассмотрим
основные понятия определения и способы вычисления моментов инерции.
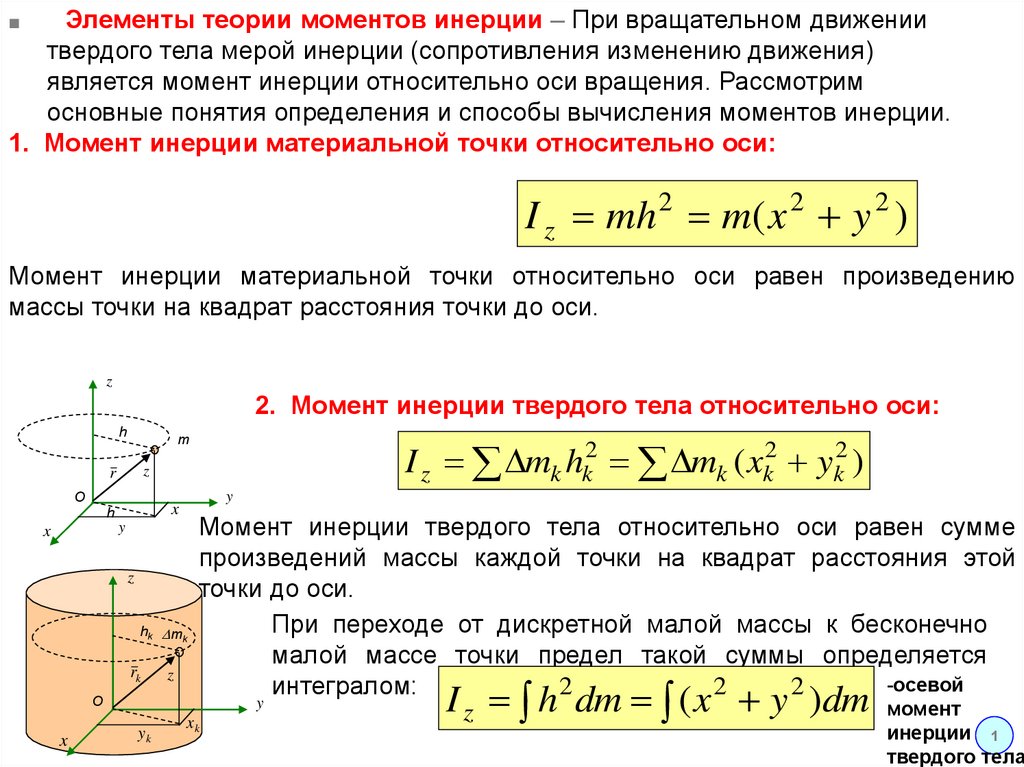
1. Момент инерции материальной точки относительно оси:
■
I z mh 2 m( x 2 y 2 )
Момент инерции материальной точки относительно оси равен произведению
массы точки на квадрат расстояния точки до оси.
z
2. Момент инерции твердого тела относительно оси:
h
m
O
y
z
hk
rk
O
x
y
x
h
x
I z mk hk2 mk ( xk2 yk2 )
z
r
yk
Момент инерции твердого тела относительно оси равен сумме
произведений массы каждой точки на квадрат расстояния этой
точки до оси.
При переходе от дискретной малой массы к бесконечно
m
малой массе точки предел такой суммы определяется
z
-осевой
2
2
2
интегралом:
y
I
h
dm
(
x
y
)
dm
момент
z
xk
k
инерции 1
твердого тела

4.

I xy xydm
- центробежный момент инерции твердого тела.
Кроме осевого момента инерции твердого тела существуют другие виды
моментов инерции:
I O r 2 dm ( x 2 y 2 z 2 )dm
- полярный момент инерции твердого тела.
3. Теорема о моментах инерции твердого тела относительно параллельных
осей – формула перехода к параллельным осям:
I z 2 ( x 22 y 22 )dm (( x1 a) 2 ( y1 b) 2 )dm ( x12 y12 )dm 2a x1dm 2b y1dm (a 2 b 2 ) dm.
z2
z1
I z1
dm
O2
d
b
x2 x
1
z
a
O1
y2
y1
x2
x1
y2
y1
Таким образом:
S y1
S x1
d2
M
I z 2 I z1 2aS y1 2bS x1 d 2 M .
Если ось z1 проходит через центр масс, то статические моменты равны нулю:
I z 2 I zC d 2 M .
2

5.

4.
Момент инерции однородного
стержня постоянного сечения
относительно оси:
Выделим элементарный объем dV = Adx
на расстоянии x:
5.
Момент инерции однородного
сплошного цилиндра относительно
оси симметрии:
Выделим элементарный объем dV = 2πrdrH
(тонкий цилиндр радиуса r) :
zС
z
R
L
z
Элементарная масса:
dm 2 rdrH
x
x
C
H
dx
Элементарная масса:
dm Adx
x3
2
2
I z x dm x Adx A
3
0
0
L
L
L
0
L3 ML2
A
3
3
Для вычисления момента инерции
относительно
центральной
оси
(проходящей через центр тяжести)
достаточно изменить расположение оси
и задать пределы интегрирования (-L/2,
L/2). Здесь продемонстрируем формулу
перехода к параллельным
осям:
I z I zC d 2 M .
2
ML2
L
I zC M .
3
2
2
I zC
ML2 L
ML2
M
.
3
12
2
R
R
I z y r dm r 2 2 rdrH
2
0
x
r
0
4 R
r
2 H
4
dr
0
R 4 MR 2
2 H
4
2
Здесь использована формула объема цилиндра
V=πR2H.
Для вычисления момента инерции пустотелого
(толстого) цилиндра достаточно задать пределы
интегрирования от R1 до R2 (R2> R1):
r4
I z 2 H
4
R2
R1
2
2
R24 R14 M ( R 2 R1 )
2 H
.
2
4 4
Поскольку высота цилиндров в результате не
входит в формулы моментов инерции, то они
остаются
справедливыми
для
тонкого
сплошного диска и обода колеса (тонкого
кольца).
3

6.

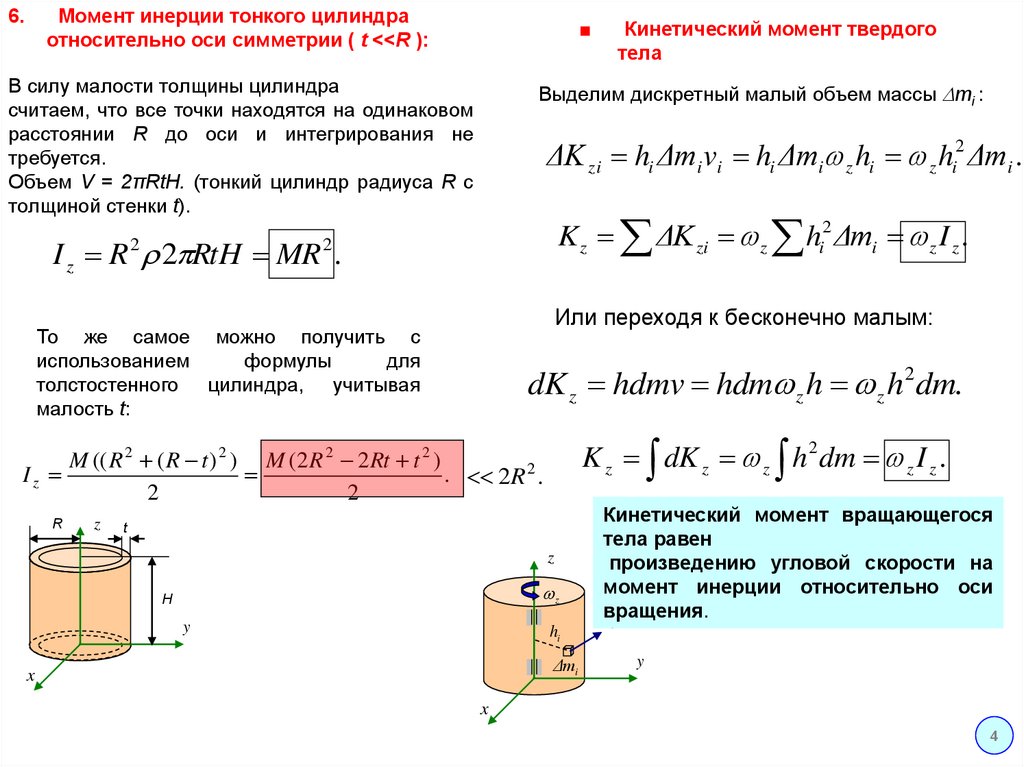
Момент инерции тонкого цилиндра
относительно оси симметрии ( t <<R ):
6.
■
В силу малости толщины цилиндра
считаем, что все точки находятся на одинаковом
расстоянии R до оси и интегрирования не
требуется.
Объем V = 2πRtH. (тонкий цилиндр радиуса R с
толщиной стенки t).
Выделим дискретный малый объем массы mi :
ΔK zi hi Δmi vi hi Δmi z hi z hi2 Δmi .
K z ΔK zi z hi2 Δmi z I z .
I z R 2 RtH MR .
2
2
Или переходя к бесконечно малым:
То же самое можно получить с
использованием
формулы
для
толстостенного цилиндра, учитывая
малость t:
dK z hdmv hdm z h z h 2 dm.
K z dK z z h 2 dm z I z .
M (( R 2 ( R t ) 2 ) M (2 R 2 2 Rt t 2 )
Iz
. 2R 2 .
2
2
R
z
Кинетический момент твердого
тела
t
z
z
H
y
hi
Δmi
x
Кинетический момент вращающегося
тела равен
произведению угловой скорости на
момент инерции относительно оси
вращения.
v
i
y
x
4

7.

Пример: Два человека одинакового веса G1 = G2 висят на канате, переброшенном через сплошной блок
весом G3 = G1/4. В некоторый момент один из них начал подниматься по канату с относительной
скоростью u. Определить скорости подъема каждого из людей.
1. Выбираем объект движения (блок с людьми):
2. Отбрасываем связи (опорное устройство блока):
3. Заменяем связь реакциями (подшипника):
R
G3
u
G1
4. Добавляем активные силы (силы тяжести):
5. Записываем теорему об изменении кинетического момента
dK z
системы относительно оси вращения блока:
M ze G1 R G2 R 0.
dt
Так как момент внешних сил равен нулю, то кинетический момент должен
оставаться постоянным:
K z const.
G2
Kz0 K z .
В начальный момент времени t = 0 было равновесие и Kz0 = 0.
После начала движения одного человека относительно каната вся система пришла в движение, но
кинетический момент системы должен остаться равным нулю: Kz = 0.
Кинетический момент системы складывается из кинетических моментов обоих людей и блока:
K z K z1 K z 2 K z 3
G1
G
(u v2 ) R 2 v2 R I 3 3 0.
g
g
Здесь v2 – скорость второго человека, равная скорости троса,
M 3 R 2 G3 R 2 G1R 2
Iz
.
2
2g
4 2g
v2
8u
.
17
3
v2
.
R
v1 u
G1
G1
G1R 2 v2
(u v2 ) R v2 R
0.
g
g
4 2g R
8u 9u
.
17 17
5

8.

■
Дифференциальное уравнение вращения твердого тело
относительно оси:
Запишем теорему об изменении
кинетического момента твердого тела,
вращающегося вокруг неподвижной
оси:
dK
z
dt
Пример: Определить период малых
свободных колебаний однородного
стержня массы M и длиной l,
подвешенного одним концом к
неподвижной оси вращения.
M ze .
l
I z M z Mg sin .
2
Кинетический момент вращающегося
твердого тела равен:
K z z I z .
Или:
Момент внешних сил относительно оси вращения
равен вращающему моменту (реакции и сила тяжести
моментов
не создают):
z
M ze M z M вращ .
z
z
Подставляем кинетический момент и
вращающий момент в теорему
Mz
y
x
d ( z I z )
M z M вращ .
dt
z
В случае малых колебаний sinφ φ:
y
x
O
С
Mgl
0 или k 2 0,
2I z
k
l
Mgl
2I x
Период колебаний:
G
I z M z M вращ .
Mg l
sin 0.
Iz 2
Момент инерции стержня:
Ml 2
Iz
.
3
T
T 2
2I x
2
2
.
k
Mgl
2l
.
3g
6