Метод интервалов. Общий метод интервалов

1.

МАТЕМАТИКА
Метод интервалов.
Общий метод
интервалов .

2.

ЛЕКЦИЯ№7
«Метод интервалов.
Общий метод интервалов.»
Литература
С.М. Никольский «Алгебра и
начала анализа: Учебник для 10
класса общеобразовательных
учреждений» §2 п. 2.7 – 2.9.

3.

План лекции:
Рациональные неравенства
Метод интервалов
Общий метод интервалов

4.

Определение
Неравенство, левая и правая части которого есть
рациональные выражения относительно x ,
называют рациональным неравенством с
неизвестным x .
(5x 1)(3 2x) 0
x2 x 6
2
3
x 1
x 5
4x - 6
>2
5-x
2x 3 7 x
2
2x 1 3 x
4
3
0
(x 2 1) 2 (3 2x)3 4 x 0

5.

Определение
Решением неравенства с неизвестным x называют
число, при подстановке которого в это неравенство
вместо x получается верное числовое неравенство.
Решить неравенство – значит найти все его
решения или показать, что их нет.

6.

Метод интервалов для решения
x x0 0
x x0 0
неравенств вида A(x) 0 и A(x) 0, где
A(x) (x xx1 )(x x2 )x 0... (x xn ),x
x1 x2 ... xn , n 1, n N.
Х
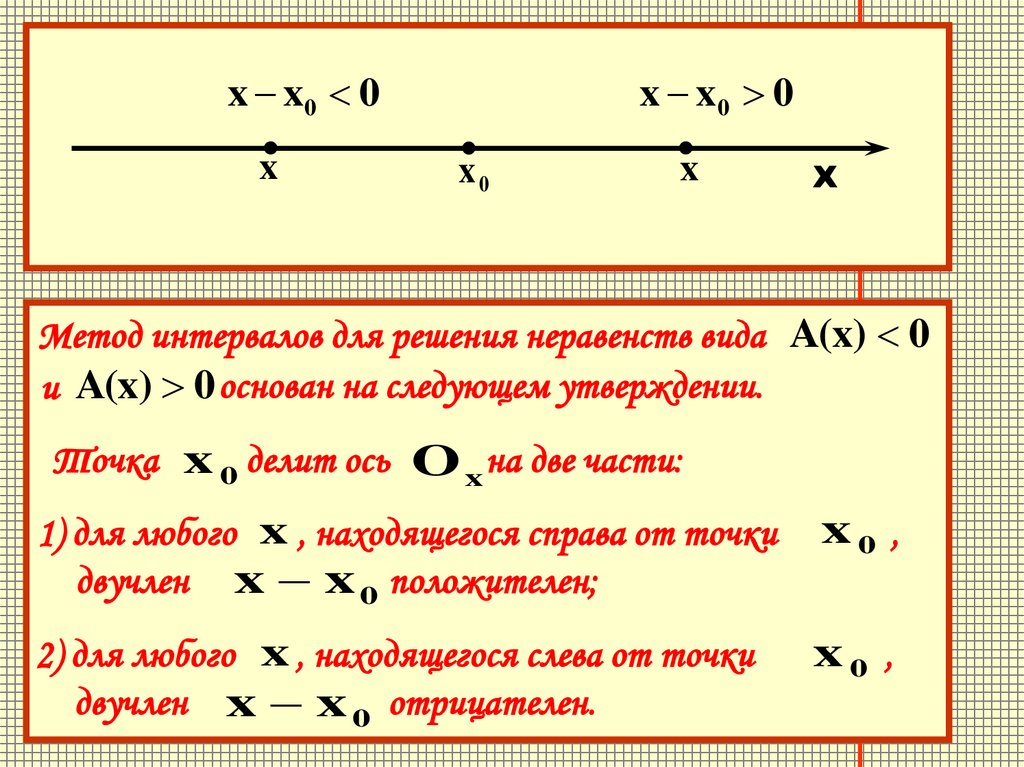
Метод интервалов для решения неравенств вида A(x) 0
и A(x) 0 основан на следующем утверждении.
Точка x 0 делит ось O x на две части:
1) для любого x , находящегося справа от точки
двучлен x x 0 положителен;
x0 ,
2) для любого x , находящегося слева от точки
двучлен x x 0 отрицателен.
x0 ,

7.

Пусть требуется решить неравенство
(x x1 )(x x 2 ) ... (x xn ) 0
Не нарушая общности, положим
(x x1 )(x x 2 )(x x 3 )(x x 4 ) 0
Тогда:
5).
Аналогично
рассуждая,
получим,
что
x,, находящегося
x 4x ,23 ии xx34
2).Для
Длялюбого
любогона
,O
находящегося
справа
от
xоси
3).
Для
любого
между
точками
4).
находящегося
между
точками
1).
Отметим
точки
нули
x
,
x
,
x
,
x
1
2
3
4
x
xотрицательны,
из
любой
двучлен
левой
части
положителен,
интервалов
(x x1 )(x два
x 2левой
)(x xчасти
неравенства.
xв неравенства
) 0 дляотрицателен.
множителя
,последние
последний
множитель
в произведении
множителей
Они
делят
ось на
3 )(x
4произведении
аПоэтому
из(x
остальных
множителей
положителен,
поэтому
поэтому
x
)(x
x
)(x
x
)(x
x
)
x
;
x
;
x
,
,
,
x
;
x
;
x
(x
x
)(x
x
)(x
x
)(x
x
)
(x
x
)(x
x
)(x
x
)(x
20
x 04,) 0
1
2
3
4
и
x
;
x
;
x
интервалы
xлюбой
;
,
,
3 2 4 1
4 1 1
2 3
31
3для
4
2
2
3
4
любого x ,
(x x1 )(x x 2 )(x x 3 )(x x 4 ) 0
для
любого
любого
x; xиз1 интервалов
.xx принадлежащего
. .
x 3 ; x x4 2 ;,интервалу
для
интервалу
x1 ; x 2. . x x
;
x
для
, принадлежащего
4 ;3
x
4
принадлежащего
интервалу
3
+
+
+
x1
-
x2
x3
-
x4
x

8.

Замечание 1.
Сами числа x1 , x 2 , x 3 , x 4 не являются решением
неравенства (x x1 )(x x 2 )(x x 3 )(x x 4 ) 0 .
Замечание 2.
Множество решений неравенств вида A(x) 0 ,
и A(x) 0где , A(x) (x x1 )(x x2 ) ... (x xn ), ,
есть
множества всех решений
n 1,объединение
n N
неравенств
иA(x) 0 иA(x)
множества
всех
0
решений уравнения
.
A(x) 0

9.

Метод интервалов для решения неравенств вида
A(x) 0 , A(x) 0 , A(x) 0, A(x) 0 ,
где A(x) (x x1 )(x x 2 ) ... (x xn ) , x1 x 2 ... xn,
n 1, n N, то есть все xk
различны.
1. Привести рациональное неравенство к одному из видов:
A(x) 0 , A(x) 0, A(x) 0 , A(x) 0, где
A(x) (x x1 )(x x2 ) ... (x xn ), n 1, n N .
2. Найти нули множителей, стоящих в левой части
неравенства, и расположить их на оси O x в
соответствующем порядке.

10.

Метод интервалов для решения неравенств вида
A(x) 0 , A(x) 0 , где A(x) (x x1 )(x x 2 ) ... (x x n ),
n 1, n N, x1 x 2 ... x n
то есть все xk различны.
3. Над промежутком справа от наибольшего нуля многочлена
поставить знак «+», так как на этом промежутке все
множители положительны. Затем, двигаясь справа налево,
при переходе через очередной нуль, сменить знак на
противоположный.

11.

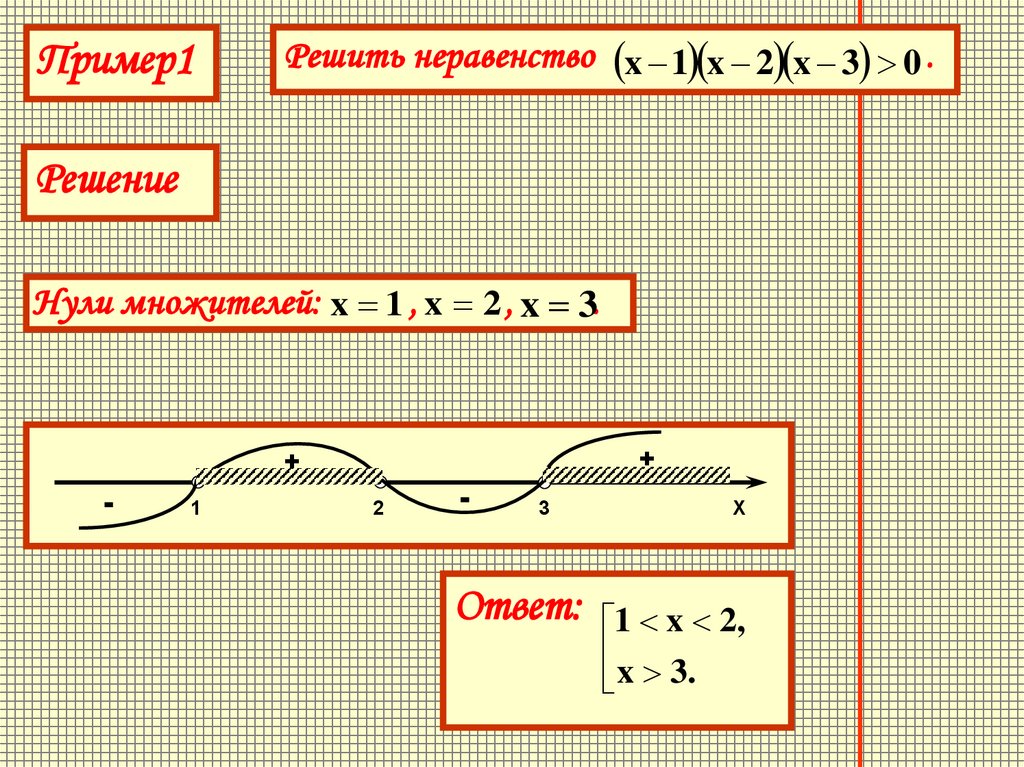
Пример1
Решить неравенство x 1 x 2 x 3 0 .
Решение
Нули множителей: x 1 , x 2 , x 3.
+
+
-
1
2
-
3
Ответ:
Х
1 x 2,
x 3.

12.

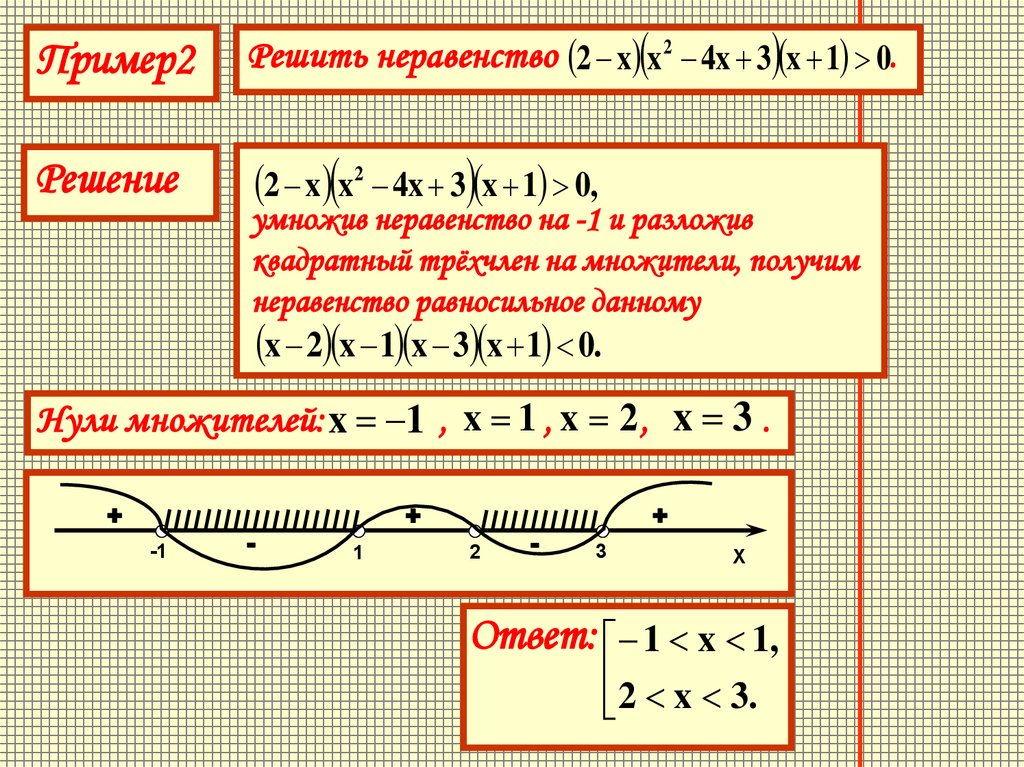
Пример2
Решить неравенство 2 x x 2 4x 3 x 1 0.
Решение
2 x x2 4x 3 x 1 0,
умножив неравенство на -1 и разложив
квадратный трёхчлен на множители, получим
неравенство равносильное данному
x 2 x 1 x 3 x 1 0.
Нули множителей: x 1 , x 1 , x 2 , x 3 .
+
-1
-
+
1
2
-
+
3
Х
Ответ: 1 x 1,
2 x 3.

13.

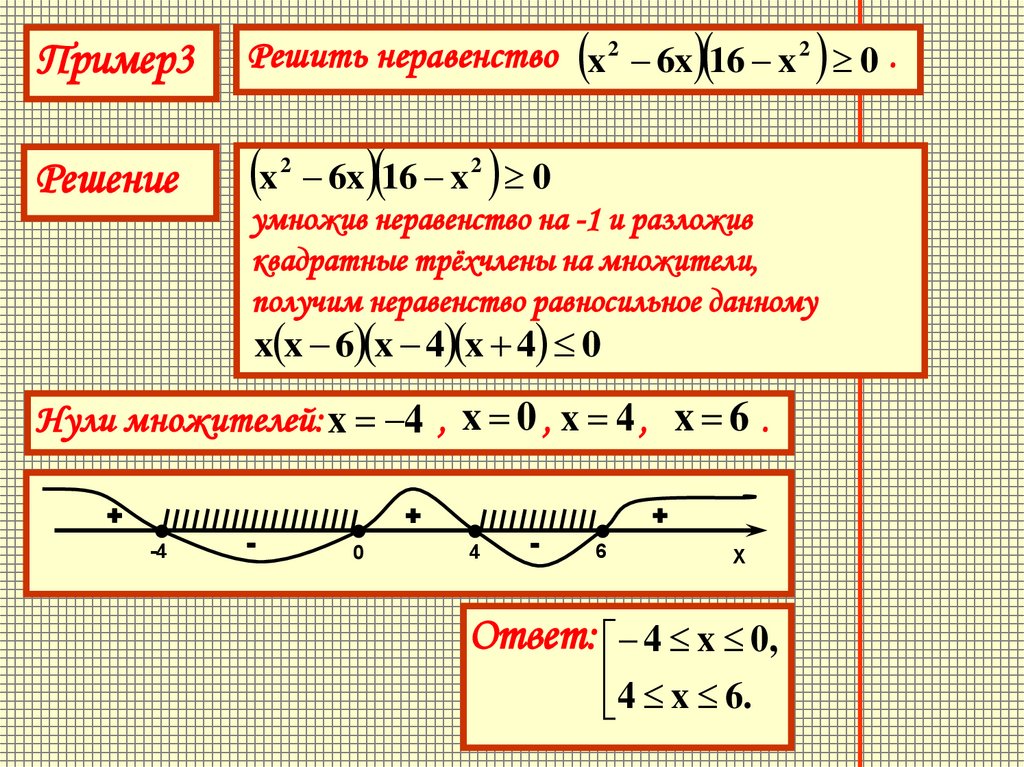
Пример3
Решить неравенство x 2 6x 16 x 2 0 .
Решение
x
2
6x 16 x 2 0
умножив неравенство на -1 и разложив
квадратные трёхчлены на множители,
получим неравенство равносильное данному
x x 6 x 4 x 4 0
Нули множителей: x 4 , x 0 , x 4 , x 6 .
+
-4
-
+
0
4
-
+
6
Х
Ответ: 4 x 0,
4 x 6.

14.

Решить неравенство
Пример4
x
x
2
2x 3 x 2 x 1 49 x 2 5x x 2 0
2x 3 x 2 x 1 49 x 2 5x x 2 0,
умножив неравенство 2 раза на -1, разложив
квадратные трёхчлены на множители и
учитывая, что x 2 x 1 0 при x R ,
получим неравенство равносильное данному
Решение
2
x 3 x 1 x 7 x 7 x x 5 0
Нули множителей: x 7 , x 1, x 0, x 3 , x 5, x 7.
+
-7
-
+
-1
0
-
+
3
5
-
Ответ:
+
7
Х
x 7,
1 x 0,
3 x 5,
x 7.

15.

Общий метод интервалов для решения неравенств
вида A(x) 0 , A(x) 0 , A(x) 0, A(x) 0,где
A(x) (x x1 )(x x 2 ) ... (x x n ), n 1, n N
если не все x1 , x 2 ,..., x n различны.
1. Привести рациональное неравенство к одному из видов:
A(x) 0 , A(x) 0, A(x) 0 , A(x) 0, где
A(x) (x x1 )(x x2 ) ... (x xn ), n 1, n N
если не все x1 , x 2 ,..., x n различны, то произведение
одинаковых двучленов записывают в виде степени этого
двучлена
A(x) (x x 1 ) k 1 (x x 2 ) k 2 ... (x x n ) k n, k m 1 ; k m N .

16.

Общий метод интервалов для решения неравенств
вида A(x) 0 , A(x) 0 , A(x) 0, A(x) 0,где
A(x) (x x1 )(x x 2 ) ... (x x n ), n 1, n N
если не все x1 , x 2 ,..., x n различны.
3. Найти
Над промежутком
справа от
наибольшего
2.
нули множителей,
стоящих
в левойнуля
части
многочлена поставить
знак их
«+»,натак
неравенства,
и расположить
оси как
O xнав этом
промежутке все множители
соответствующем
порядке. положительны. Затем,
двигаясь справа налево, при переходе через очередной нуль,
сменить знак на противоположный, если
соответствующий этому нулю двучлен возведён в
нечётную степень, и сохранить знак, если
соответствующий этому нулю двучлен возведён в чётную
степень.

17.

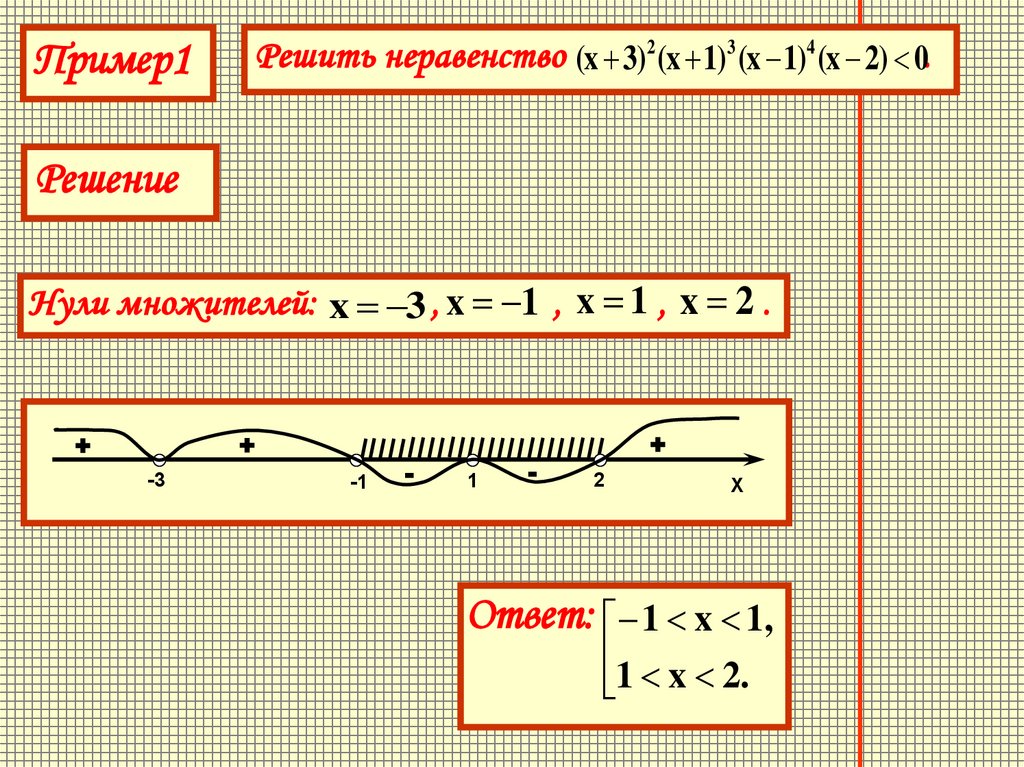
Пример1
Решить неравенство (x 3)2 (x 1)3 (x 1)4 (x 2) 0.
Решение
Нули множителей: x 3 , x 1 , x 1 , x 2 .
+
+
-3
-1
-
1
-
+
2
Х
Ответ: 1 x 1,
1 x 2.

18.

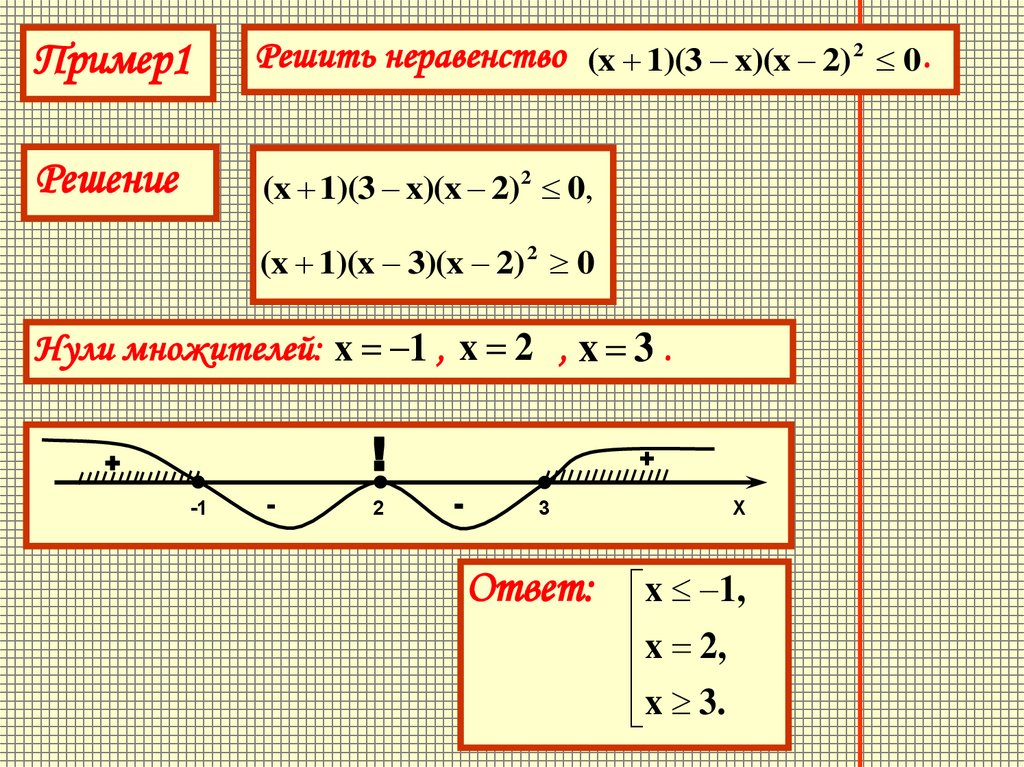
Пример1
Решить неравенство (x 1)(3 x)(x 2) 2 0 .
Решение
(x 1)(3 x)(x 2)2 0,
(x 1)(x 3)(x 2) 2 0
Нули множителей: x 1 , x 2 , x 3 .
!
+
-1
-
2
+
-
Х
3
Ответ: x 1,
x 2,
x 3.

19.

Метод интервалов для решения неравенств вида
A(x)
A(x)
0и
0 , где A(x)и B(x)
B(x)
B(x)
разлагаются в
произведения разных двучленов вида x x 0 .
Замечание 1.
Неравенство
A(x)
0 равносильно
B(x)
неравенство
A(x)
0
B(x)
неравенству A(x) B(x) 0 ,
равносильно неравенству A(x) B(x) 0 .

20.

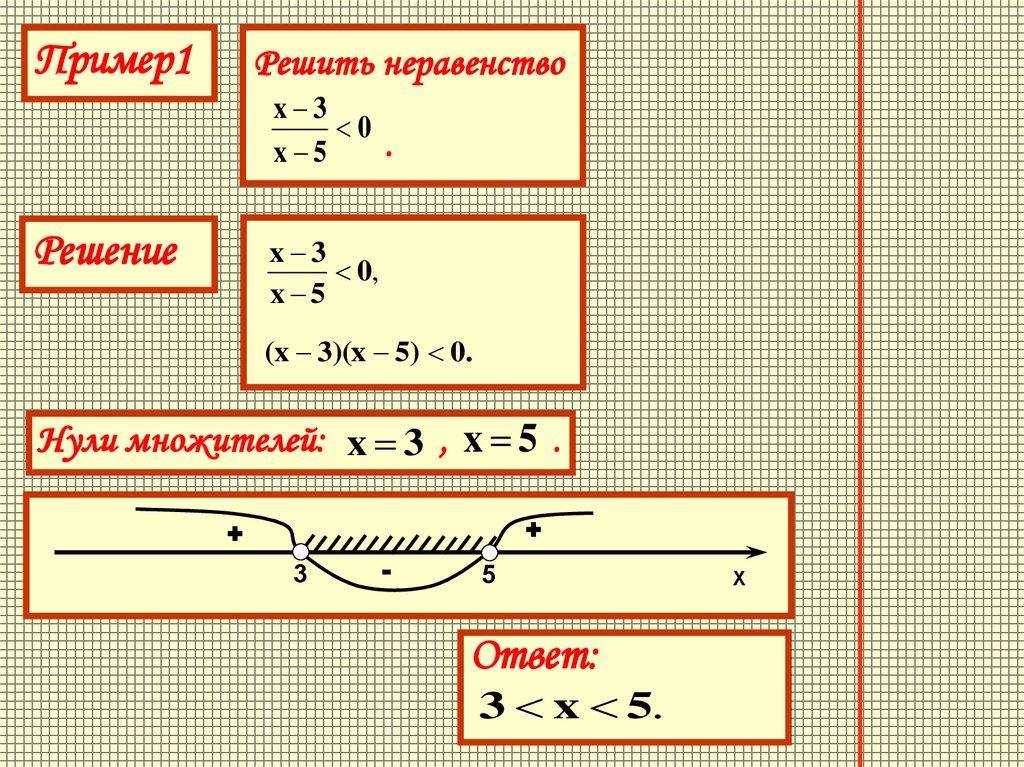
Пример1
Решить неравенство
x 3
0
x 5
Решение
.
x 3
0,
x 5
(x 3)(x 5) 0.
Нули множителей: x 3 , x 5 .
+
+
3
-
5
Ответ:
3 x 5.
Х

21.

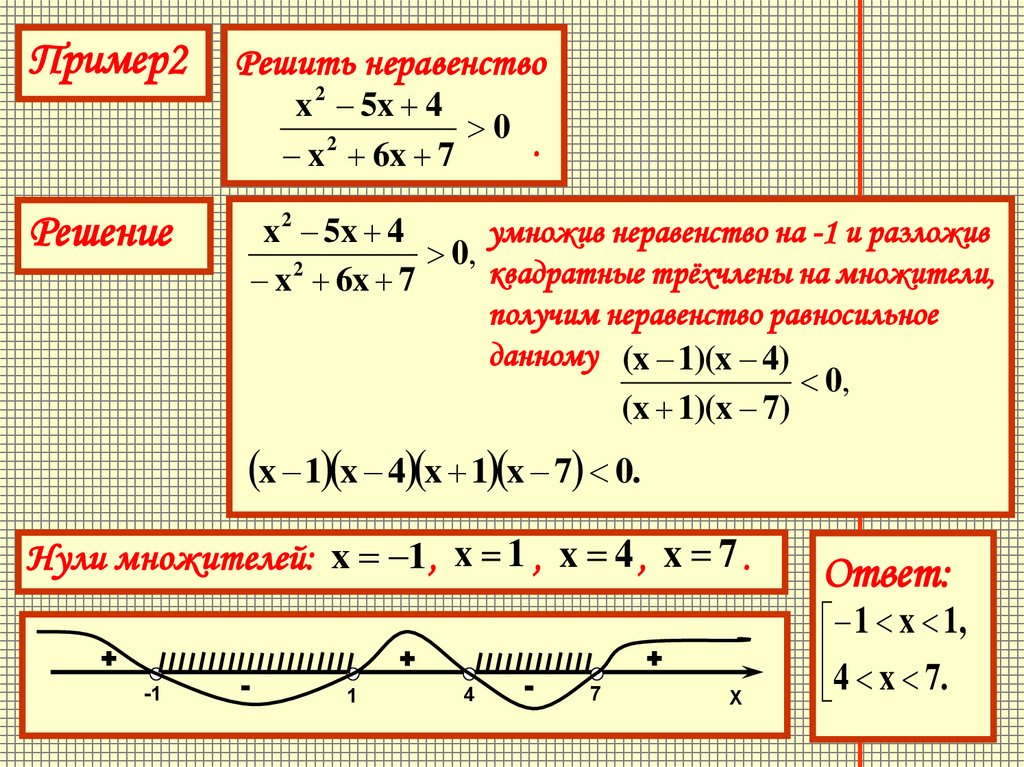
Пример2
Решить неравенство
x 2 5x 4
0
2
.
x 6x 7
x 2 5x 4
умножив неравенство на -1 и разложив
0,
2
квадратные трёхчлены на множители,
x 6x 7
получим неравенство равносильное
данному (x 1)(x 4)
0,
(x 1)(x 7)
Решение
x 1 x 4 x 1 x 7 0.
Нули множителей: x 1, x 1 , x 4 , x 7 .
+
-1
-
+
1
4
-
+
7
Х
Ответ:
1 x 1,
4 x 7.

22.

Пример3
Решить неравенство
x
1
2x 3 x
Решение
.
x
1
,
2x 3 x
x
1
0,
2x 3 x
x 2 2x 3
0,
x(2x 3)
(x 1)(x 3)
0,
x(2x 3)
x 2 (2x 3)
0,
x(2x 3)
x 1 x 3 x 2x 3 0.
Нули множителей: x 1,5, x 1, x 0, x 3.
+
+
+
-1,5
-
-1
0
-
3
Х
Ответ:
x 1,5,
1 x 0,
х 3.

23.

Метод интервалов для решения неравенств вида
A(x)
A(x)
0и
0 , где A(x)и B(x)
B(x)
B(x)
разлагаются в
произведения двучленов, где в числителе и
знаменателе дроби имеются одинаковые
двучлены x x 0 .
Не нарушая общности положим, что неравенство
имеет вид
(x x 1 ) k 1 (x x 2 ) ... (x x n )
0
k2
(x x 1 ) (x x 2 ) ... (x x m )
тогда его можно представить в виде
(x x 2 ) ... (x x n )
0
k 1 k 2
(x x 1 )
(x x 2 ) ... (x x m )
.
A(x)
0
B(x)

24.

Пример1
Решить неравенство
x
2
5x
x 3 x 2 (x 3)(x 2)
Решение
.
x 2 5x 6
0,
(x 3)(x 2)
(x 2)(x 3)
0,
(x 3)(x 2)
x 3
0,
2
(x 3)(x 2)
x 3 x 3 x 2 2 0.
x
2
5x
,
x 3 x 2 (x 3)(x 2)
x
2
5x
0,
x 3 x 2 (x 3)(x 2)
x(x 2) 2(x 3) 5x
0,
(x 3)(x 2)
Нули множителей: x 3 , x 2 , x 3 .
Ответ:
+
+
-3
-
2
-
3
Х
3 x 2,
2 x 3.

25.

Замечание.
Множество решений неравенств вида A(x) 0 ,
B(x)
A(x)
0 есть объединение множества всех
B(x)
решений неравенств A(x) 0 , A(x) 0 и
B(x)
B(x)
A(x)
0.
множества всех решений уравнения
B(x)

26.

Пример1
Решение
(ЦТ 2000 г.)Найти число целых решений
8x 3
1
2
неравенства
2
2
(x 2x 1)(x x 6)
8x 3
1
2
,
2
2
(x 2x 1)(x x 6) x x 2
8x 3
1
2
0,
2
2
(x 2x 1)(x x 6) x x 2
8x 3
1
0,
2
(x 1) (x 3)(x 2) (x 2)(x 1)
8x 3 (x 1)(x 3)
0,
2
(x 1) (x 3)(x 2)
x x 2
x 2 4x
0,
2
(x 1) (x 3)(x 2)
x(x 4)
0,
2
(x 1) (x 3)(x 2)
x x 4 x 1 2 x 3 x 2 0,
x 1 2 x 3 x 2 0.

27.

Пример1
(ЦТ 2000 г.)Найти число целых решений
8x 3
1
2
неравенства
2
2
Решение
(x 2x 1)(x x 6)
x(x 4)
0
2
(x 1) (x 3)(x 2)
x x 2
2
x 3 x 2 0,
x
x
4
x
1
2
x 3 x 2 0.
x
1
Нули числителя: x 0, x 4 .
Итак
Нули знаменателя: x 3 , x 1 , x 2 .
+
+
-3
-
-1
-
0
Целые решения: x 2 ; 0 ; 3 ; 4.
+
2
-
4
Х
3 x 1,
1 x 0,
2 х 4.
Ответ: 4 целых решения.

28.

Домашнее задание
1) Материал лекций 1 –7.
2) Галицкий М.Л. «Сборник задач по алгебре
для 8 – 9 классов» §8
№ 8.54в), г); 8.72; 8.90; 8.96.
3) Сборник для подготовки к ЦТ. Тема № 6.