Похожие презентации:
Модель многоотраслевой экономики В. Леонтьева
1.
Модель Леонтьевамногоотраслевой экономики
2.
Макроэкономика функционированиямногоотраслевого хозяйства
требует баланса между отдельными отраслями.
Каждая отрасль, с одной стороны, является
производителем, а с другой — потребителем
продукции, выпускаемой другими отраслями.
Возникает довольно
непростая задача расчета связи между
отраслями через выпуск и потребление
продукции разного рода.
3.
Впервые эта проблема была сформулированав 1936 г. в виде математической модели в
трудах известного американского
экономиста В. Леонтьева, который
попытался проанализировать причины
экономической депрессии в США 1929—
1932 гг. Эта модель основана на алгебре
матриц и использует аппарат матричного
анализа.
4.
Балансовые соотношенияДля простоты будем полагать, что
производственная сфера хозяйства
представляет собой п отраслей, каждая из
которых производит свой однородный
продукт. Для обеспечения своего
производства каждая отрасль нуждается в
продукции других отраслей
(производственное потребление). Обычно
процесс производства рассматривается за некоторый период времени; в ряде случаев такой
единицей служит год.
5.
6.
7.
Линейная модельмногоотраслевой экономики
8.
9.
10.
11.
Введем в рассмотрение векторы-столбцыобъемов произведенной продукции (вектор
валового выпуска), объемов продукции
конечного потребления (вектор конечного
потребления) и матрицу коэффициентов
прямых затрат:
12.
13.
14.
Уравнение межотраслевого баланса можноиспользовать в двух целях.
В первом, наиболее простом случае, когда
известен вектор валового выпуска х,
требуется рассчитать вектор конечного
потребления у.
15.
Во втором случае уравнение межотраслевогобаланса используется для целей планирования
со следующей формулировкой задачи: для
периода времени Г (например, год) известен
вектор конечного потребления у и требуется
определить вектор х валового выпуска. Здесь
необходимо решать систему линейных
уравнений (2.8) с известной матрицей А и
заданным вектором у. В дальнейшем мы
будем иметь дело именно с такой задачей.
16.
Между тем система (2.8) имеет рядособенностей, вытекающих из прикладного
характера данной задачи; прежде всего —
все элементы матрицы А и векторов х и у
должны быть неотрицательными. В
таком случае и модель Леонтьева
называется продуктивной.
17.
Для уравнения типа (2.8)
разработана соответствующая
математическая теория исследования
решения и его особенностей. Укажем
некоторые основные ее моменты.
Перепишем систему (2.8) с использованием
единичной матрицы Е в виде
18.
19.
Если существует обратная матрица (Е А)'\ то существует и единственноерешение уравнения (2.8)
20.
21.
• Существует несколько критериевпродуктивности матрицы А. Приведем два из
них.
• 1. Матрица А продуктивна тогда и только
тогда, когда матрица (Е — Л)"1 существует
и ее элементы неотрицательны.
• 2. Матрица А с неотрицательными
элементами продуктивна, если сумма
элементов по любому ее столбцу (строке) не
превосходит единицы:
22.
причем хотя бы для одного столбца (строки) эта сумма строго меньшеединицы.
23.
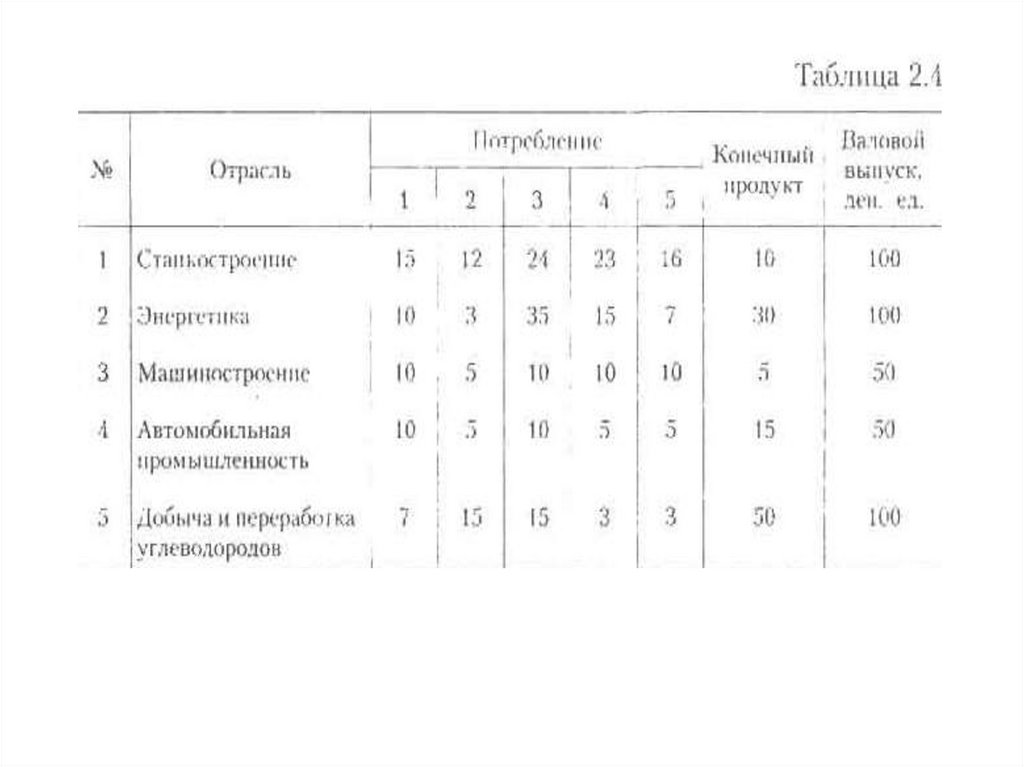
• Пример 1. В табл. 2.4 приведены данныепо балансу за некоторый период времени
между пятью отраслями промышленности.
Найти векторы конечного потребления и
валового выпуска, а также матрицу
коэффициентов прямых затрат и
определить, является ли она продуктивной
в соответствии с приведенными выше
критериями.
24.
25.
26.
Все элементы матрицы Аположительны, однако нетрудно видеть,
что их суммы в третьем и четвертом
столбцах больше единицы. Следовательно,
условия второго критерия продуктивности
не соблюдены,и матрица А не является
продуктивной. Экономическая причина
этой непродуктивности заключается в том,
что внутреннее потребление отраслей 3 и 4
слишком велико в соотношении с их
валовыми выпусками.
27.
• Пример 2. Таблица 2.5 содержит данныебаланса трех отраслей промышленности за
некоторый период времени. Требуется
найти объем валового выпуска каждого
вида продукции, если конечное
потребление по отраслям увеличить,
соответственно, до 60, 70 и 30 условных
денежных единиц.
28.
29.
Решение. Выпишем векторы валовоговыпуска и конечного потребления и
матрицу коэффициентов прямых затрат.
30.
31.
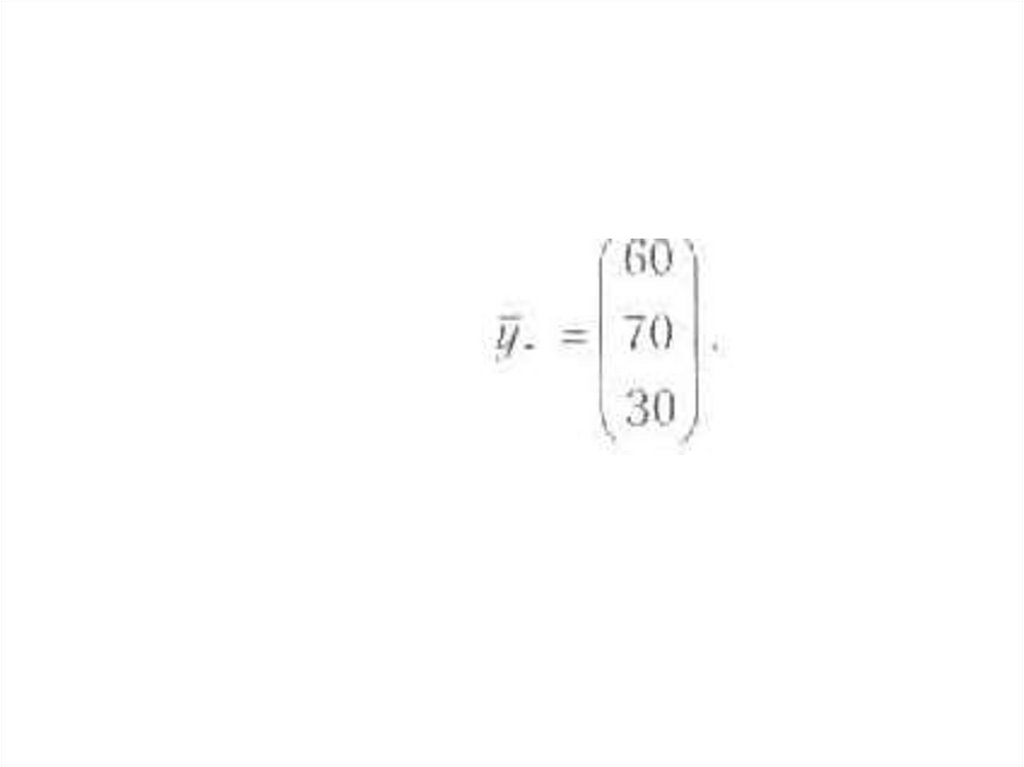
Матрица А удовлетворяет обоимкритериям продуктивности. В случае
заданного увеличения конечного
потребления новый вектор конечного
продукта будет иметь вид
32.
33.
Требуется найти новый вектор валовоговыпуска х., удовлетворяющий
соотношениям баланса в предположении,
что матрица А не изменяется. В таком
случае компоненты х,, х2, Х3 неизвестного
вектора х находятся из системы уравнений,
которая в матричной форме имеет
следующий вид:
34.
35.
36.
• Решение системы линейных уравнений призаданном векторе правой части (например,
методом Гаусса) дает новый вектор х, как
решение уравнений межотраслевого
баланса:
37.
38.
• Таким образом, для того чтобы обеспечитьзаданное увеличение компонент вектора
конечного продукта, необходимо увеличить
соответствующие валовые выпуски: добычу
и переработку углеводородов на 52,2 %,
уровень энергетики — на 35,8 % и выпуск
машиностроения —на 85 % — по
сравнению с исходными величинами.
39.
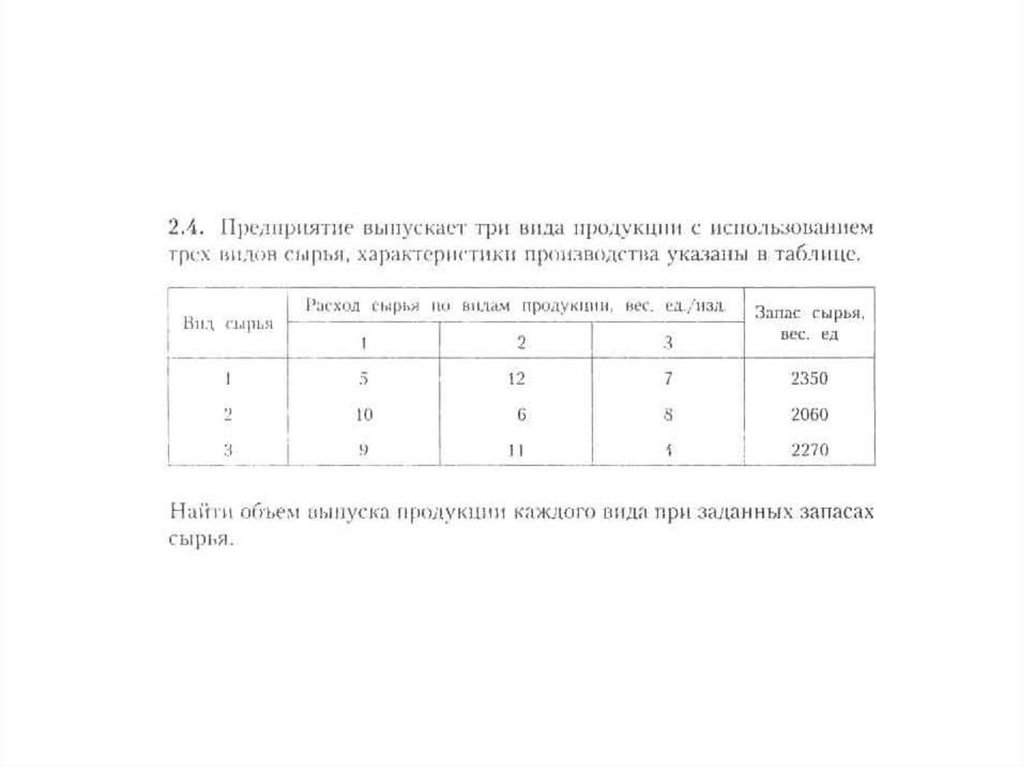
Упражнения1. По данным табл. 1 составить новую таблицу
производственно-экономических показателей по
следующим условиям:
— количество изделий всех видов увеличивается на 20 %;
— норма времени изготовления по всем изделиям
уменьшается на 20 %;
— цена на все виды изделий уменьшается на 10 %.
Найти ежесуточные показатели, указанные в задаче 1 из 1,
а также
их процентные изменения.
40.
2. По данным табл. 2 составить новую таблицупо следующим
условиям:
— дневная производительность всех
предприятий увеличивается на
100%,
— число рабочих дней в году для 1-го
предприятия увеличивается на
50 %, а для остальных — на 40 %,
— цены на виды сырья уменьшаются,
соответственно, на 10, 20 и 30 %.
Определить суммы финансирования
предприятий и их соответствующие процентные изменения.

















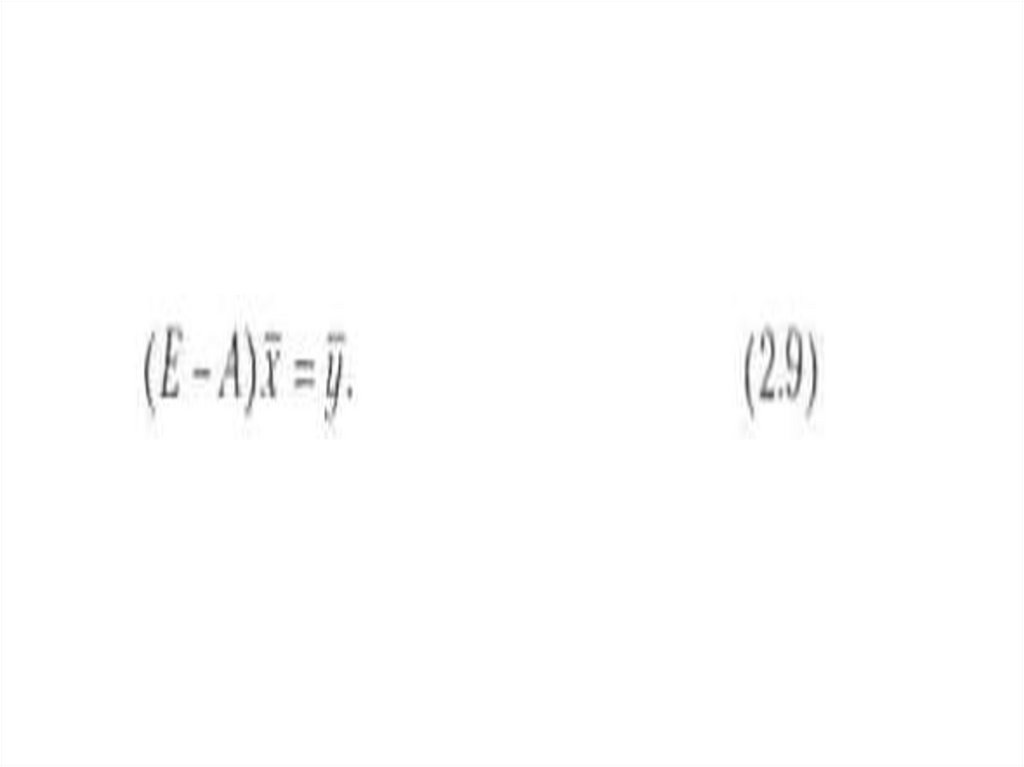










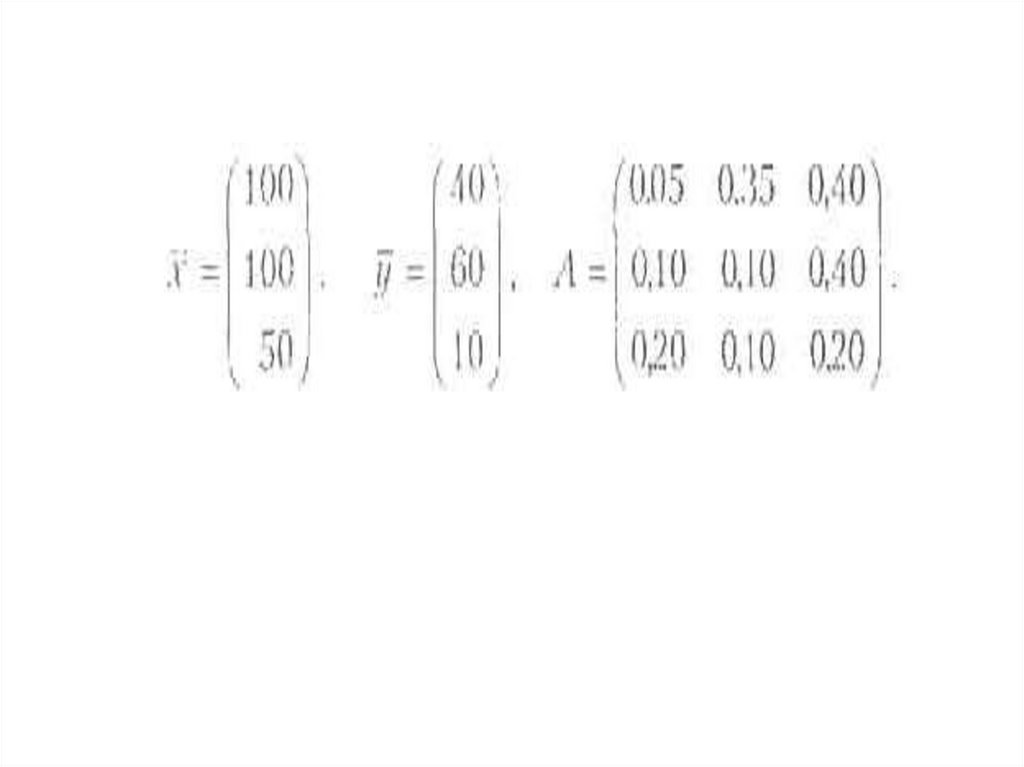


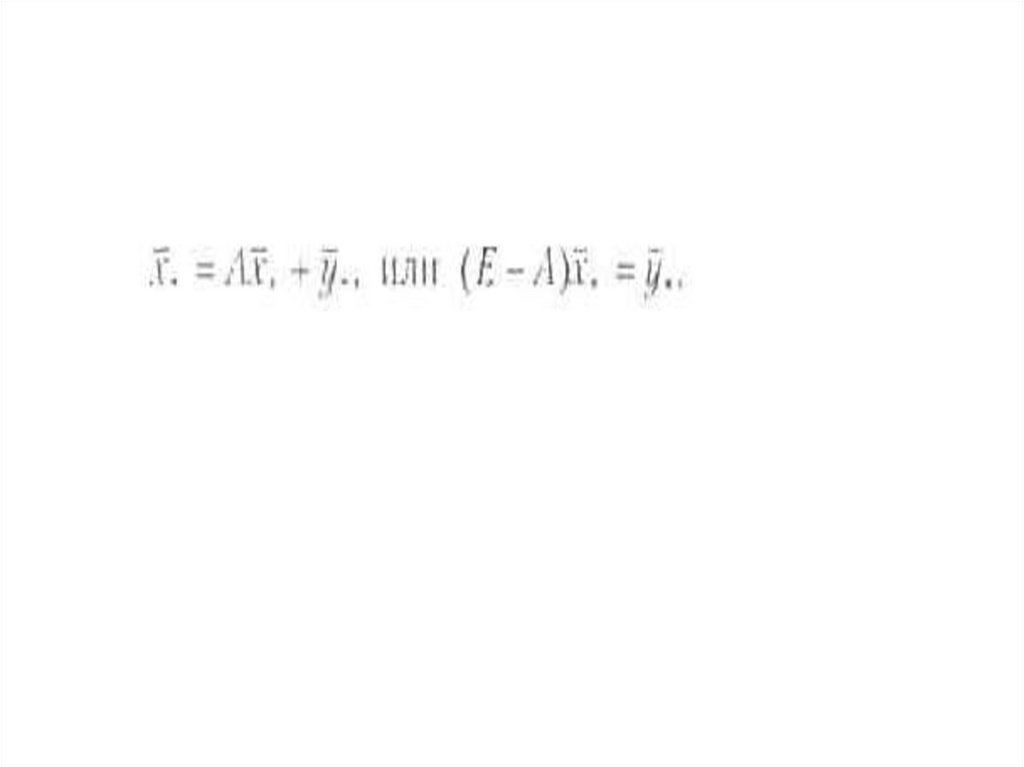







 Экономика
Экономика








