Похожие презентации:
Тригонометрические функции и их свойства
1.
2.
1 2x
y
М
1
0 2
0
-1
-y
-1 3
1
2
0
-x
М1
2
3
2
-1
2
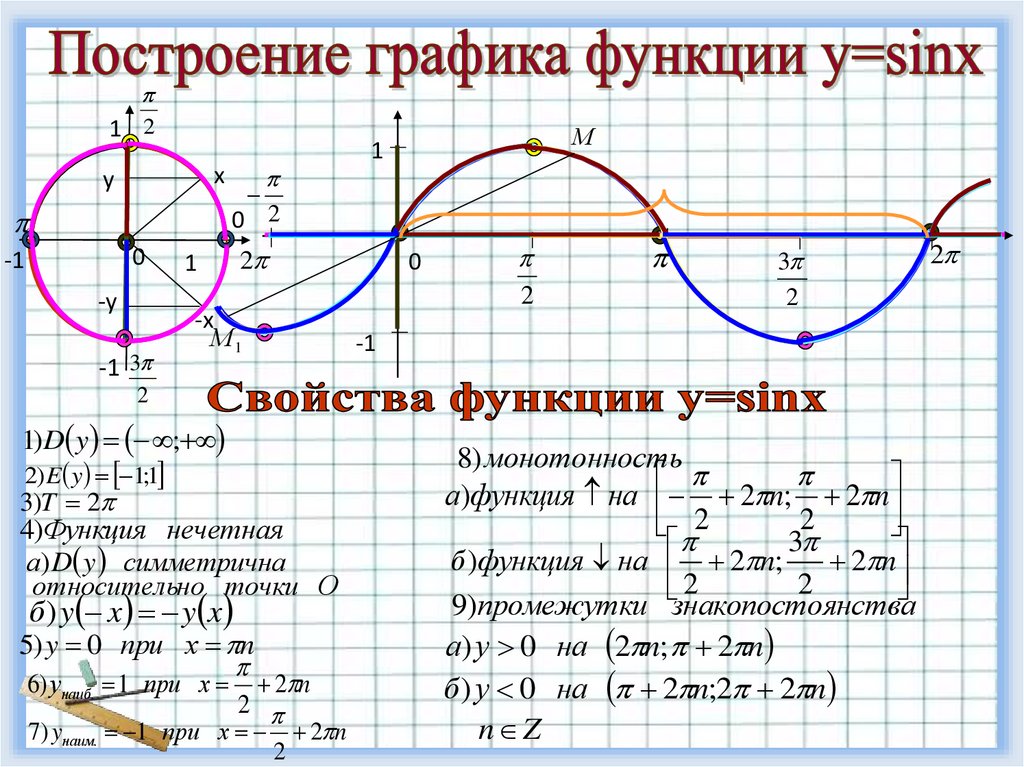
1) D y ;
2) E y 1;1
3)T 2
4)Функция нечетная
а) D y симметрична
относительно точки О
б) y x y x
5) y 0 при х n
6) унаиб. 1 при х
2 n
2
7) yнаим. 1 при х
2
2 n
8) монотонность
а)функция на 2 n; 2 n
2
2
3
б )функция на 2 n;
2 n
2
2
9)промежутки знакопостоянства
а) у 0 на 2 n; 2 n
б ) у 0 на 2 n;2 2 n
n Z
2
3.
1 25
6
1
2
6
1
0
0
-1
7
6
3
2
1) sin x 0
х n
2) sin x 1
2
2
2 n
3) sin x 1
x 2 n
2
7
6
6
0
1 2
Частные случаи:
x
6
1
2
-1
2
5
6
-1
2 n
6
5
x
2 n
6
sin x
x
x
6
1
2
2 n
7
2 n
6
13
6
5
2
17
6
3
sin x a, где 1 a 1
1
sin x
2
x
2
3
2
x 1 arcsin a n, n Z
n
x 1 arcsin
n
6 n
1
n;
2
x 1n
1
n
x 1 arcsin n;
2
x 1
n 1
6
n
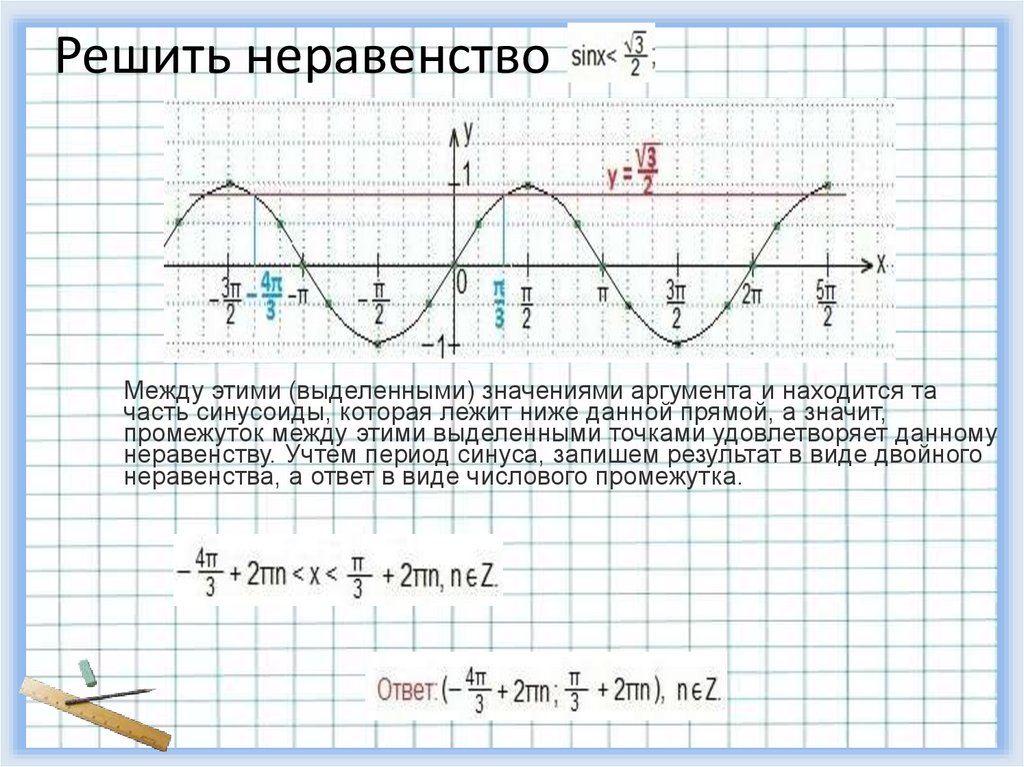
4. Решить неравенство
Между этими (выделенными) значениями аргумента и находится тачасть синусоиды, которая лежит ниже данной прямой, а значит,
промежуток между этими выделенными точками удовлетворяет данному
неравенству. Учтем период синуса, запишем результат в виде двойного
неравенства, а ответ в виде числового промежутка.
5.
1 21
x
1 0
-1
y
0
2
2
0
-x
-1
2
-1
3 2
2
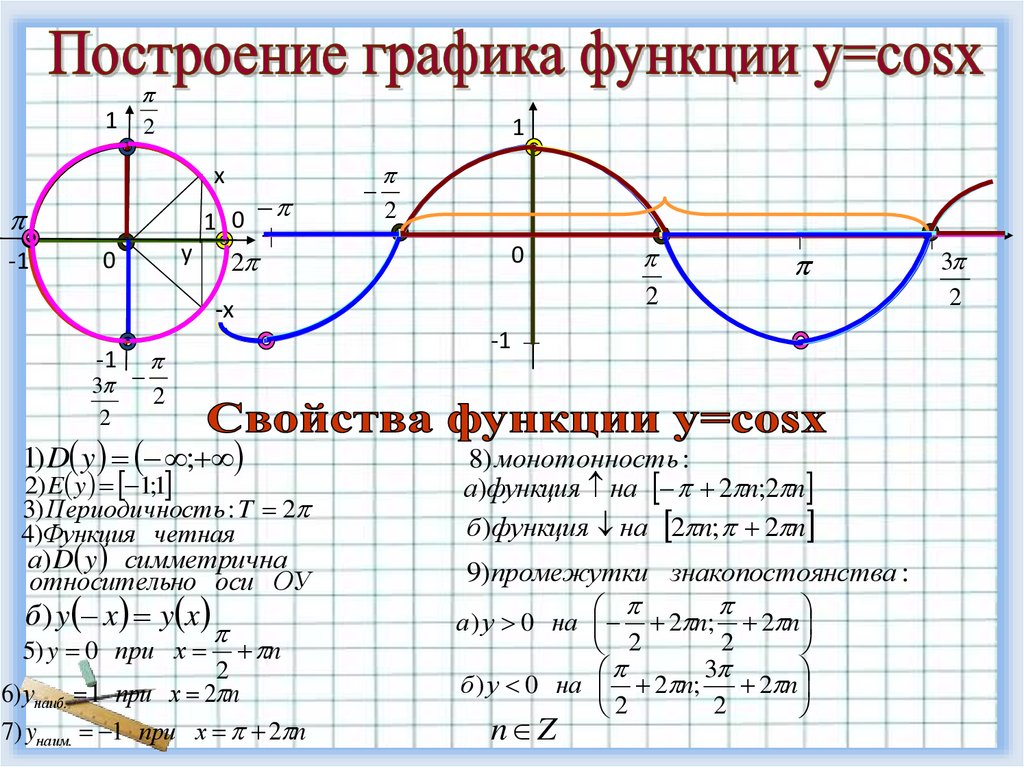
1) D y ;
2) E y 1;1
3) Периодичность : T 2
4)Функция четная
8) монотонность :
а)функция на 2 n;2 n
б )функция на 2 n; 2 n
б) y x y x
9)промежутки знакопостоянства :
а) у 0 на 2 n; 2 n
а) D y симметрична
относительно оси ОУ
5) y 0 при х
n
2
6) унаиб. 1 при х 2 n
7) yнаим. 1 при х 2 n
2
2
3
б ) у 0 на 2 n;
2 n
2
2
n Z
3
2
6.
23
1 2
3
1 2
0
-1
2
3
0
1
2
1
2
1
-1
3
2
x
2
n
2) cos x 1
х 2 n
3) cos x 1
x 2 n
2
3
1
2
2
0
3
2
3
1
2
2 n
3
x 2 n
3
1
2
2
x
2 n
3
2
x
2 n
3
cos x
3 5
2 3
7 5
3 2
cos x a, где 1 a 1
1
cos x
2
x
8
3
2
4
3
3 2
-1
3
Частные случаи:
1) cos x 0
x arccos a 2 n, n Z
x arccos
x
3
1
2 n;
2
2 n
1
x arccos n;
2
1
x arccos 2 n;
2
x
2
2 n
3
7.
tgx1 2
1
x у
1 0
2
-1
0
-х -у
-1
3
2
0
2
3
2
-1
2
2
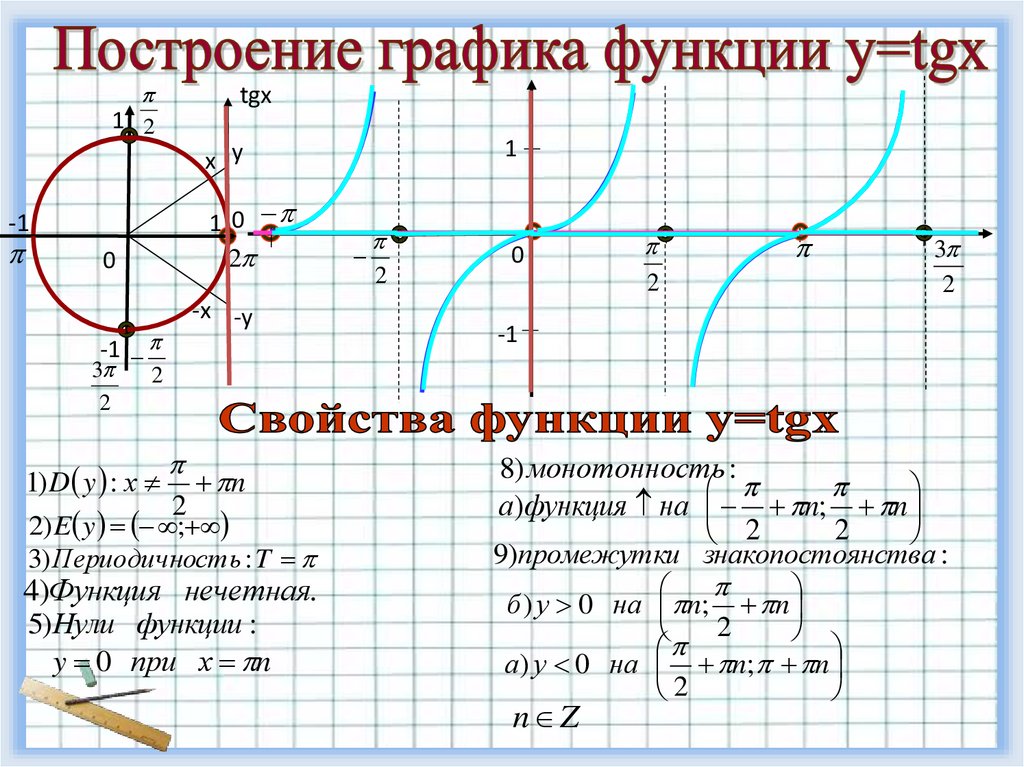
1) D y : х n
2
2) E y ;
3) Периодичность : T
4)Функция нечетная.
5) Нули функции :
y 0 при х n
8) монотонность :
а)функция на n; n
2
2
9)промежутки знакопостоянства :
б ) у 0 на n; n
2
а) у 0 на n; n
2
n Z
8.
tgx1 2
1
x а
1 0
2
-1
0
-1
3
arctga
2
-х -а
0
arctga
2
3
2
-1
2
2
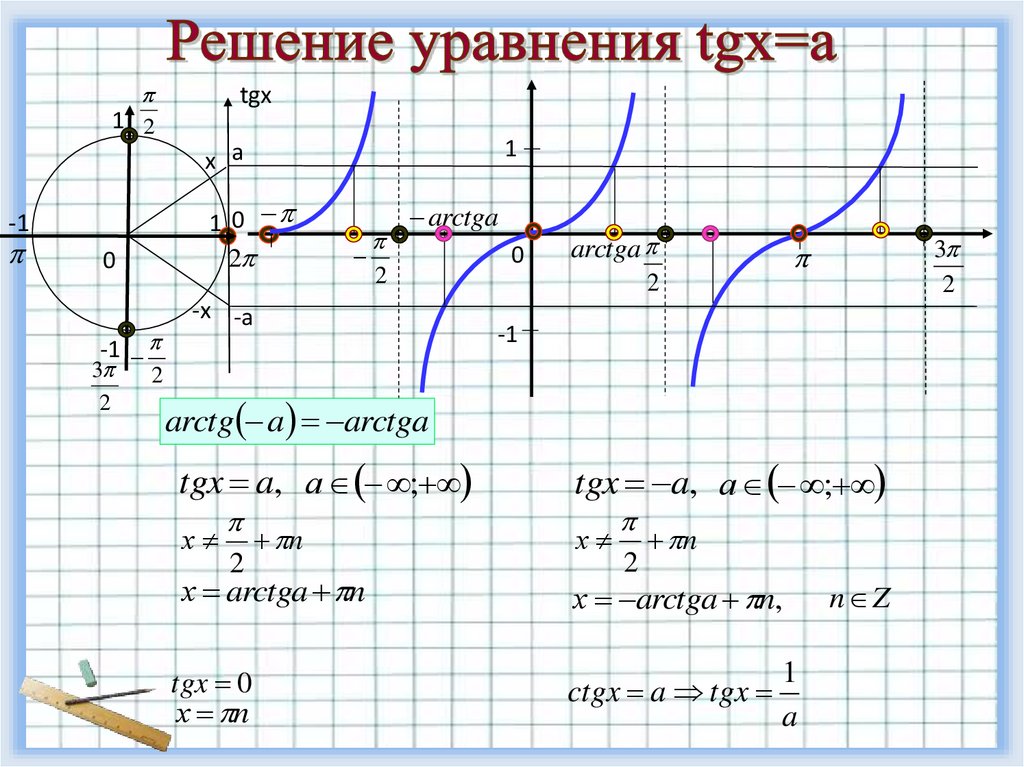
arctg a arctga
tgx a, а ;
х
2
n
х arctga n
tgx 0
х n
tgx a, а ;
х
2
n
х arctga n,
1
ctgx a tgx
a
n Z
9.
-yy
1 2
x
1 0 2
-1
1
0
2
-х
-1
0
2
3
2
2
-1
3 2
2
1) D y : х n
2) E y ;
3) Периодичность : T
4)Функция нечетная
5) Нули функции :
y 0прих n
8) монотонность :
а)функция на n; n
9)промежутки знакопостоянства
б ) у 0на n; n
2
а) у 0на n; n
2
n Z




 Математика
Математика








