Похожие презентации:
Параллельность прямой и плоскости. Решение задач
1. Решение задач по теме «Параллельность прямой и плоскости»
аα
2. Повторение:
• Какиепрямые
в
пространстве
называются
параллельными? Какие отрезки в пространстве
называются параллельными?
• Всегда ли через две параллельные прямые можно
провести плоскость? А через две пересекающиеся
прямые?
• В пространстве дано число п параллельных между собой
прямых. Известно, что никакие три из них не лежат в
одной плоскости. Сколько различных плоскостей можно
провести через эти прямые?
• Сформулируйте лемму о пересечении плоскости
параллельными прямыми.
• Каково может быть взаимное расположение прямой и
плоскости в пространстве?
• В каком случае прямая параллельна плоскости?
3.
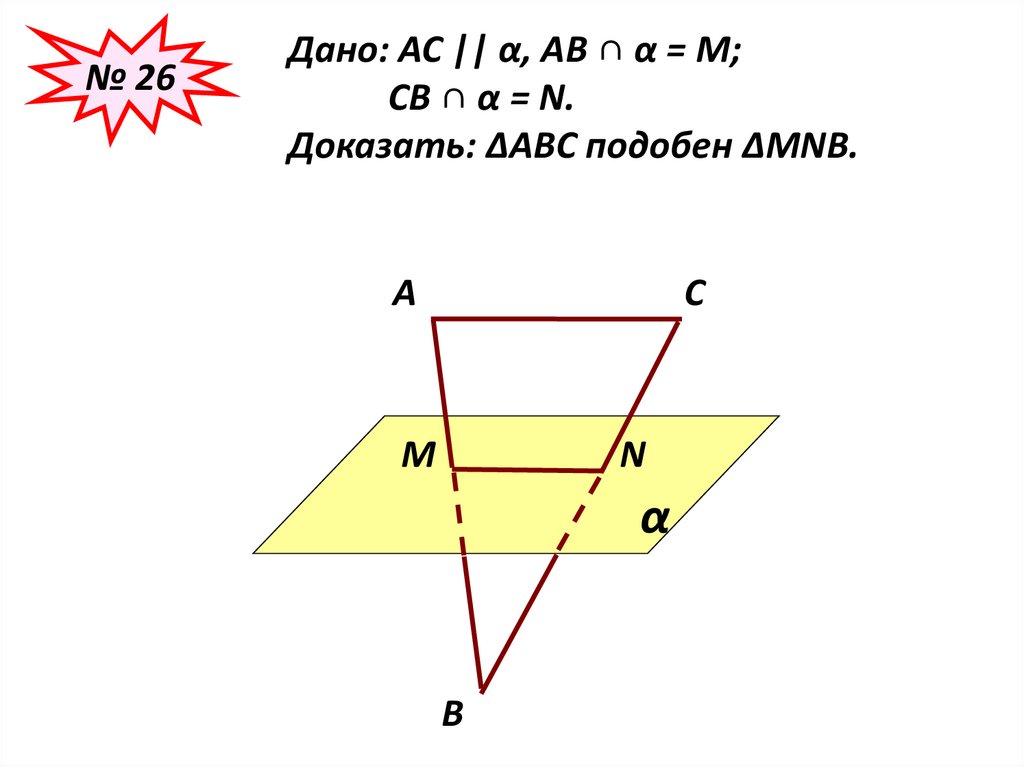
№ 26Дано: АС || α, АВ ∩ α = М;
СВ ∩ α = N.
Доказать: ∆АВС подобен ∆МNВ.
А
С
М
N
α
В
4.
Доказательство:5. Задача № 1.
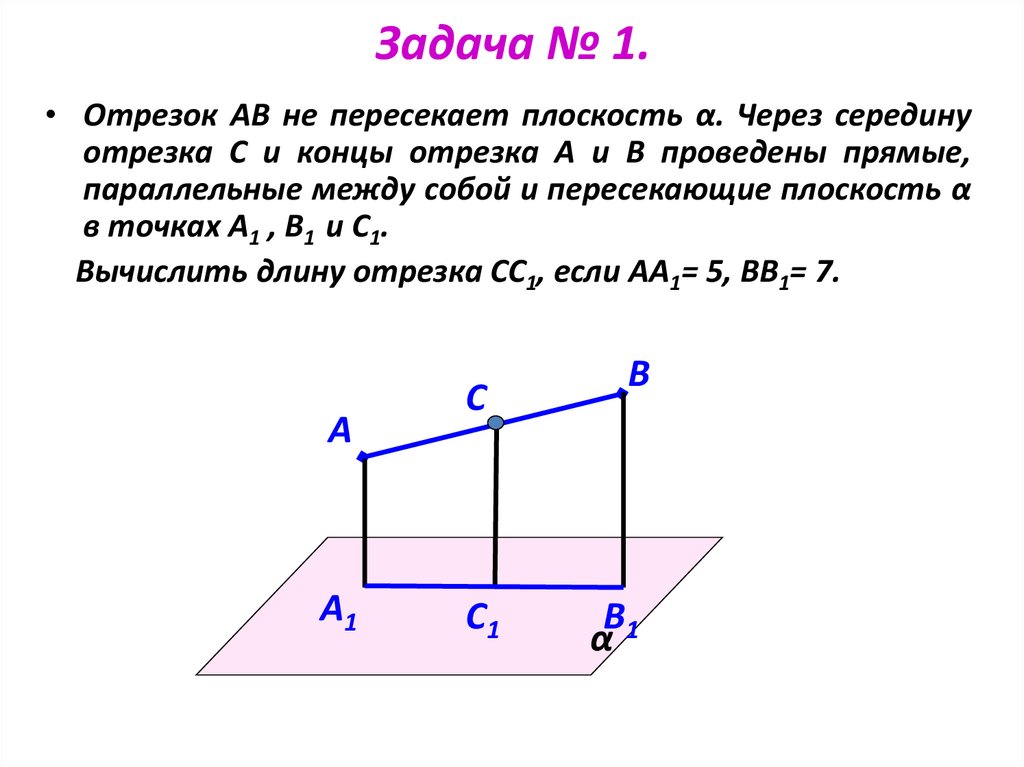
• Отрезок АВ не пересекает плоскость α. Через серединуотрезка С и концы отрезка А и В проведены прямые,
параллельные между собой и пересекающие плоскость α
в точках А1 , В1 и С1.
Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7.
А
А1
С
С1
В
В1
α
6. Задача № 2.
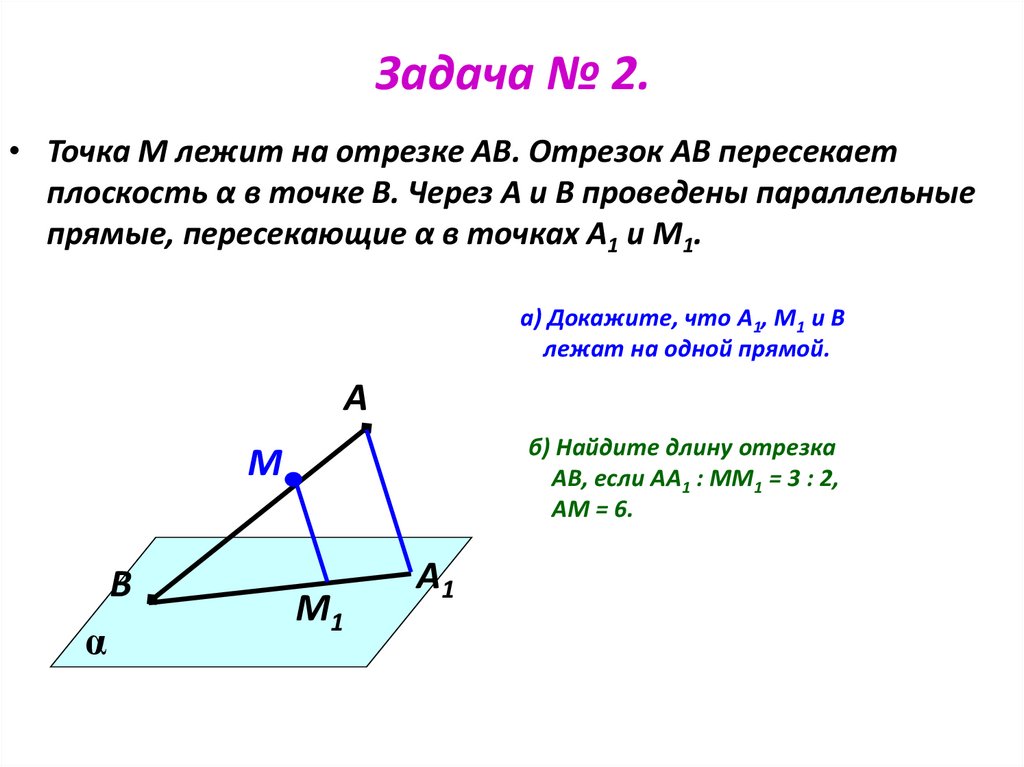
• Точка М лежит на отрезке АВ. Отрезок АВ пересекаетплоскость α в точке В. Через А и В проведены параллельные
прямые, пересекающие α в точках А1 и М1.
а) Докажите, что А1, М1 и В
лежат на одной прямой.
А
б) Найдите длину отрезка
АВ, если АА1 : ММ1 = 3 : 2,
АМ = 6.
М
В
α
М1
А1
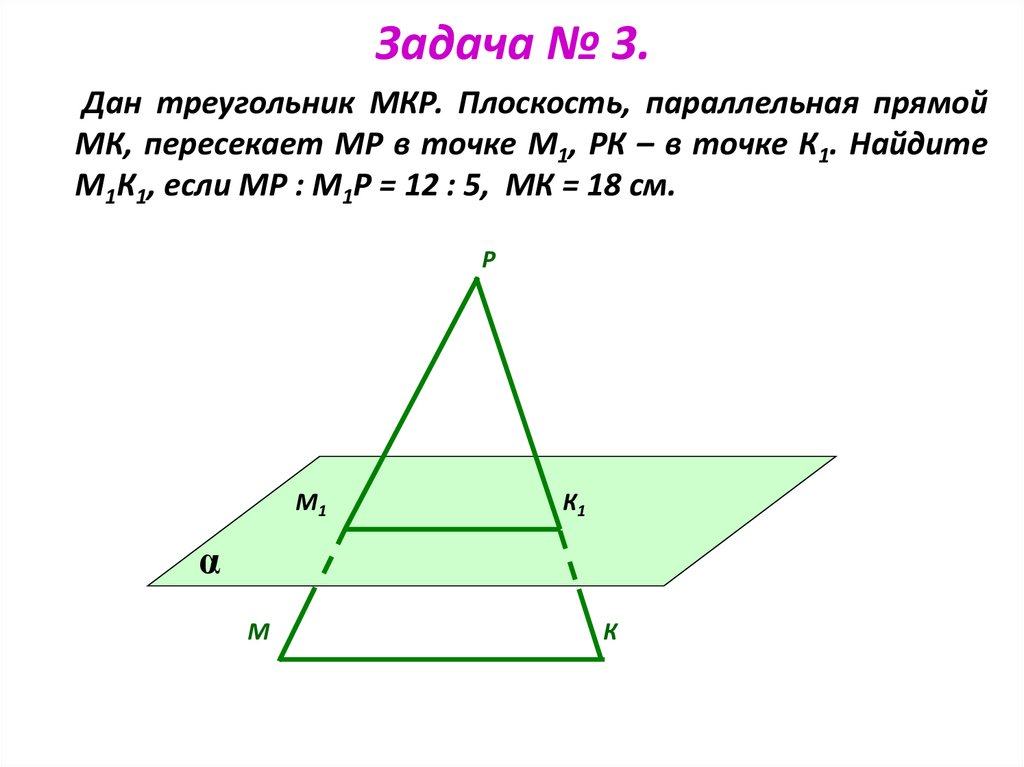
7. Задача № 3.
Дан треугольник МКР. Плоскость, параллельная прямойМК, пересекает МР в точке М1, РК – в точке К1. Найдите
М1К1, если МР : М1Р = 12 : 5, МК = 18 см.
Р
М1
К1
α
М
К
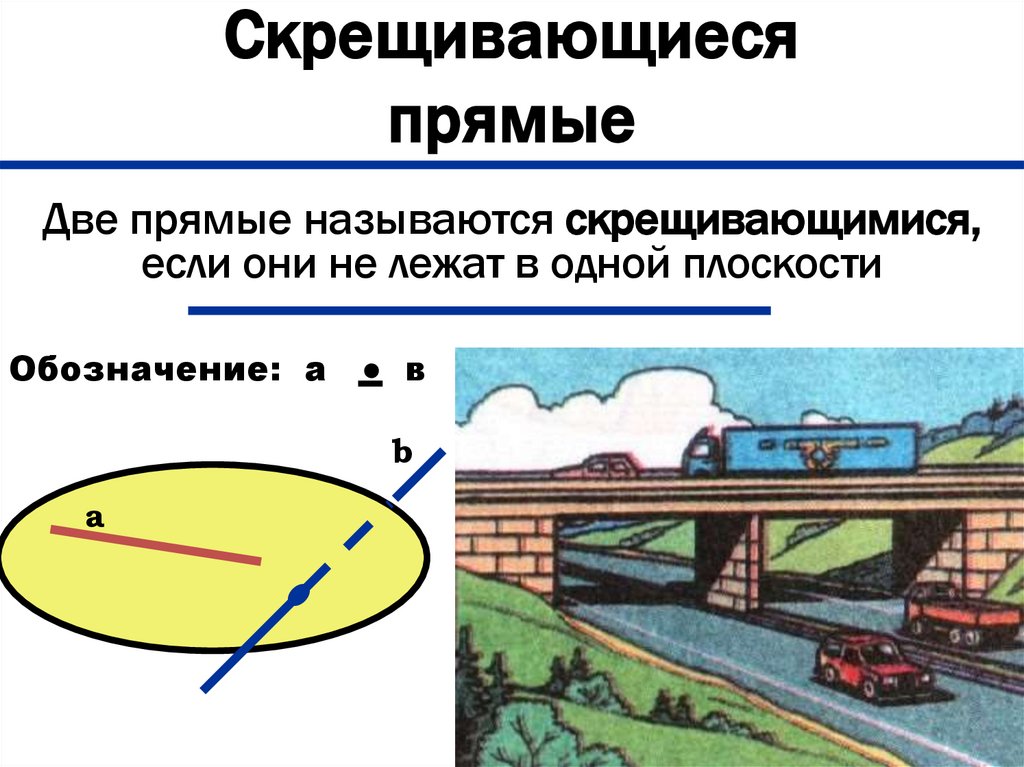
8. Скрещивающиеся прямые
Две прямые называются скрещивающимися,если они не лежат в одной плоскости
Обозначение: а
● в
b
а
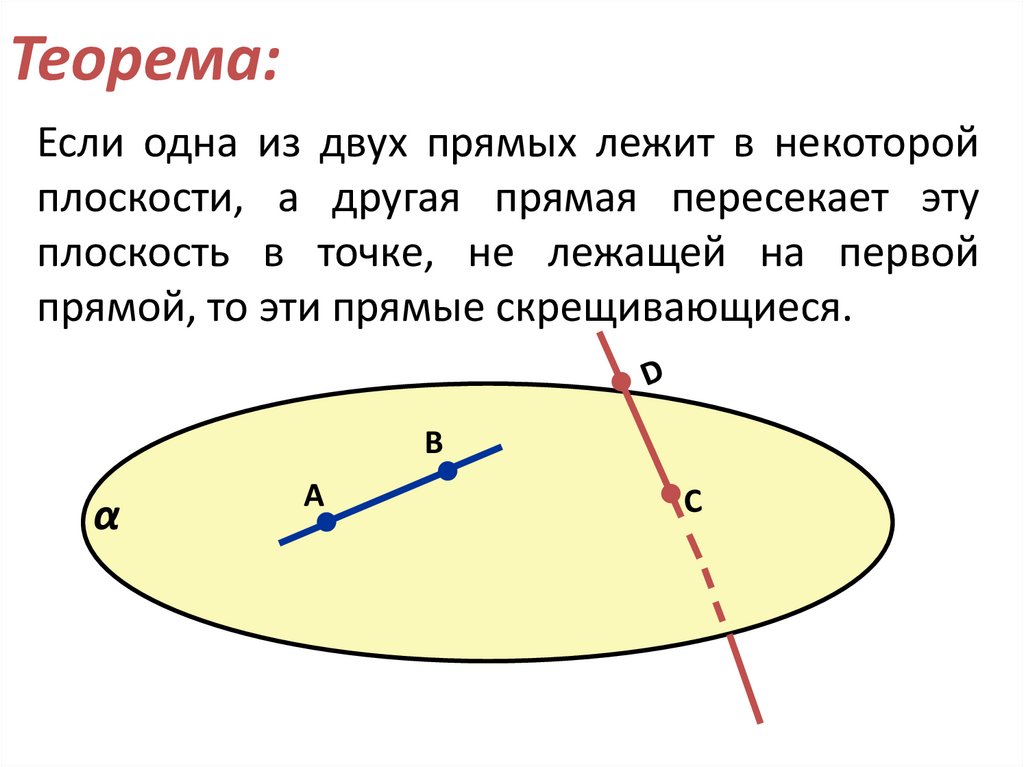
9. Теорема:
Если одна из двух прямых лежит в некоторойплоскости, а другая прямая пересекает эту
плоскость в точке, не лежащей на первой
прямой, то эти прямые скрещивающиеся.
В
α
А
10.
Работа с учебником:1) Выполнить самост. работу по вариантам и выслать решение
в WhatsApp (в «личку» или в Дневник.ru, или на почту по
адресу kireyeva1222@mail.ru) в течении 20 минут;
2) п. 7, записать конспект (опред. + признак + теорема о
скрещив. прямых);
3) № 24, 28, 31*.



 Математика
Математика








