Похожие презентации:
Логарифмічна функцiя, ii графiк та властивостi
1.
y=logabУ
У
Х
Х
y = logаx
2.
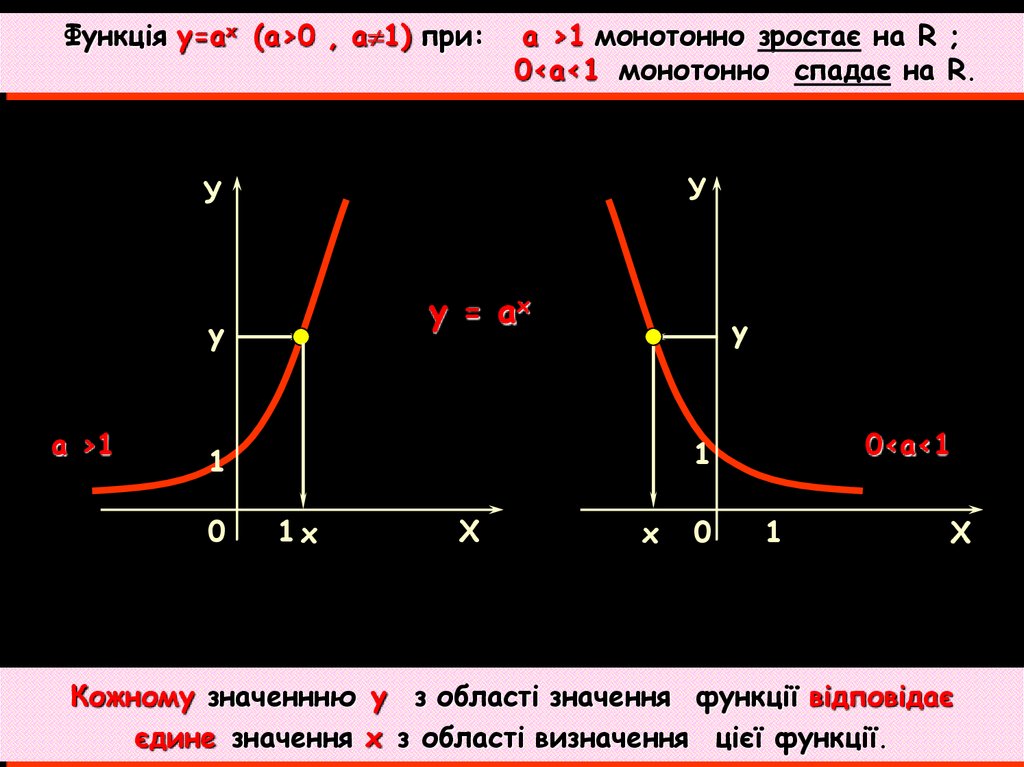
Функція у=ах (a>0 , a 1) при:a >1 монотонно зростає на R ;
0<a<1 монотонно спадає на R.
У
У
y = аx
у
a >1
у
0
0<a<1
1
1
1х
Х
х
0
1
Х
Кожному значеннню у з області значення функції відповідає
єдине значення х з області визначення цієї функції.
3.
Нехай маємо функцію у=ах , а>0, a 1.Поміняємо місцями х і у. Дістанемо: х=ау .
За означенням логарифма: y=logaх.
Означення:
Функцію, яку можна задати формулою
y = logax ( а 0, а 1 ),
називають логарифмічною функцією.
4.
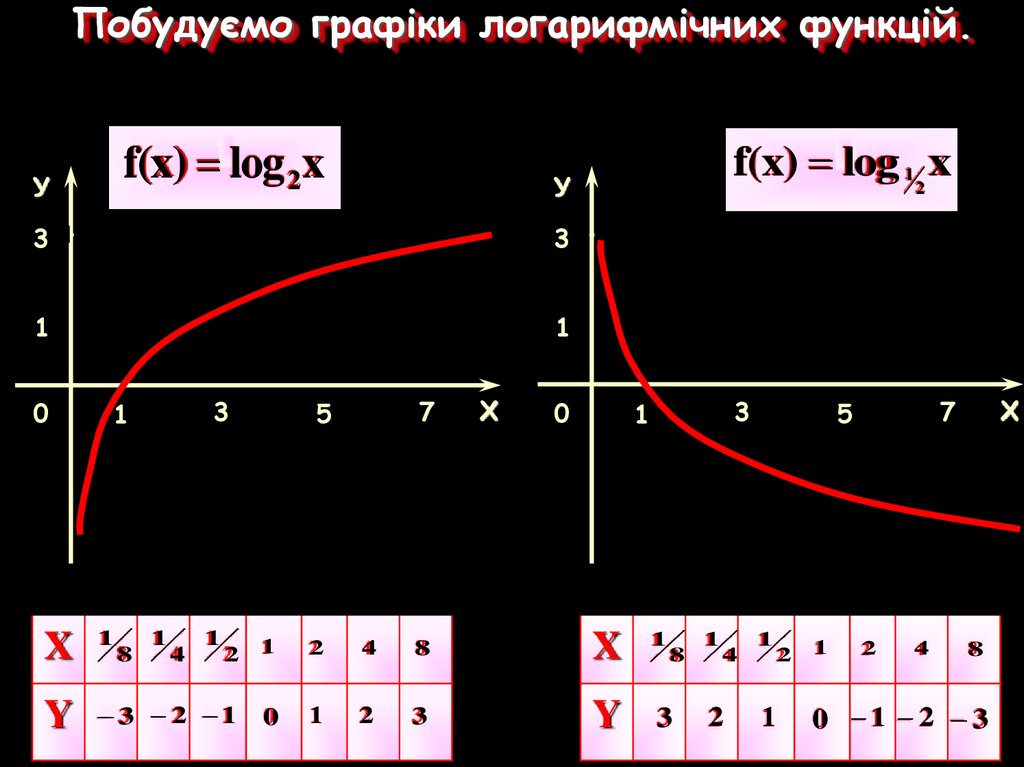
Побудуємо графіки логарифмічних функцій.f(x) log 2 x
У
3
3
1
1
0
3
1
Х
0
3
1
1
2
1
2
4
8
X
1
Y
3 2 1
0
1
2
3
Y
3
4
1
7
5
X
8
1
f(x) log 1 2 x
У
8
1
4
2
1
1
2
1
Х
7
5
2
4
8
0 1 2 3
5.
При(a 0, a 1)
g(x)=ax
f(x)= logax
D(g)=R
D(f)=(0; )
E(g)=(0; )
E(f)=R
За означенням функції
g(x)=ax, a 0, a 1 и f(x)=log ax, a 0, a 1
є взаємно оберниними.
6.
Властивості функції1.
при a>1
при 0<a<1
(0; ∞);
Область визначення
R
2. Область значень
3. Парність, непарність
Є ні парною, ні непарною
y=0 при x=1
4. Нулі функції
5. Проміжки
знакосталості:
6. Екстремуми
Проміжки монотон7. ності при x (0; ):
8. Асимптота
y>0 при x (1; );
y<0 при x (0;1);
немає
Функція
зростає
Функція
спадає
x=0
У
У
0
y>0 при x (0;1);
y<0 при x (1; );
1
Х
a>1
y = logаx ,
0
1
Х
0<a<1
7.
Графіки взаємно обернених функційсиметричні відносно прямої у=x
У
g(x)
f(x)
1
0
h(x)
Х
1
g(x)
У
h(x)
1
0
Х
1
f(x)
при a>1
при 0<a<1
8.
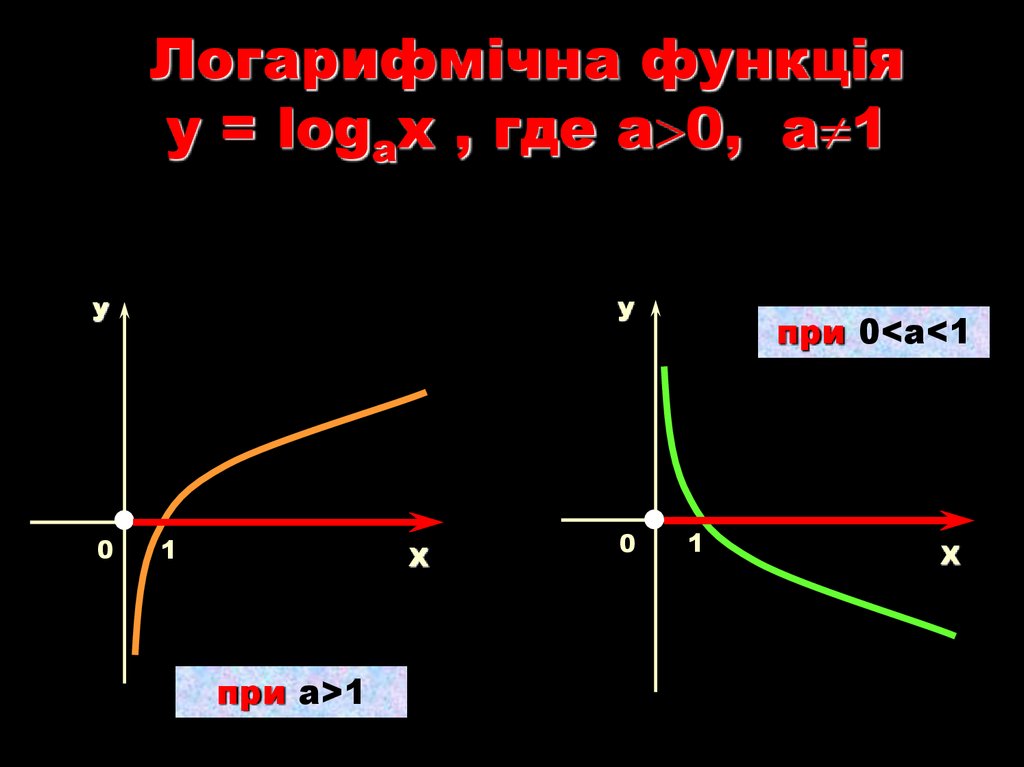
Логарифмічна функціяy = logаx , где а 0, а 1
У
У
0
1
Х
при a>1
0
при 0<a<1
1
Х
9.
При якому значенні аргумента х функції мають змістy log a ( x)
( ;0)
x 0; x 0.
y log a x
(0; )
x 0; x 0.
y log a (x 1)
(1; )
x 1 0; x 1.
y log a (x 2 1)
y log a (x 1)
2
y log a x
( ; 1) (1; )
R
( ;0) (0; )
x 1,
x 2 1 0;
.
x
1
x 2 1 0,
при x R.
x 0,
x 0;
.
x
0
10.
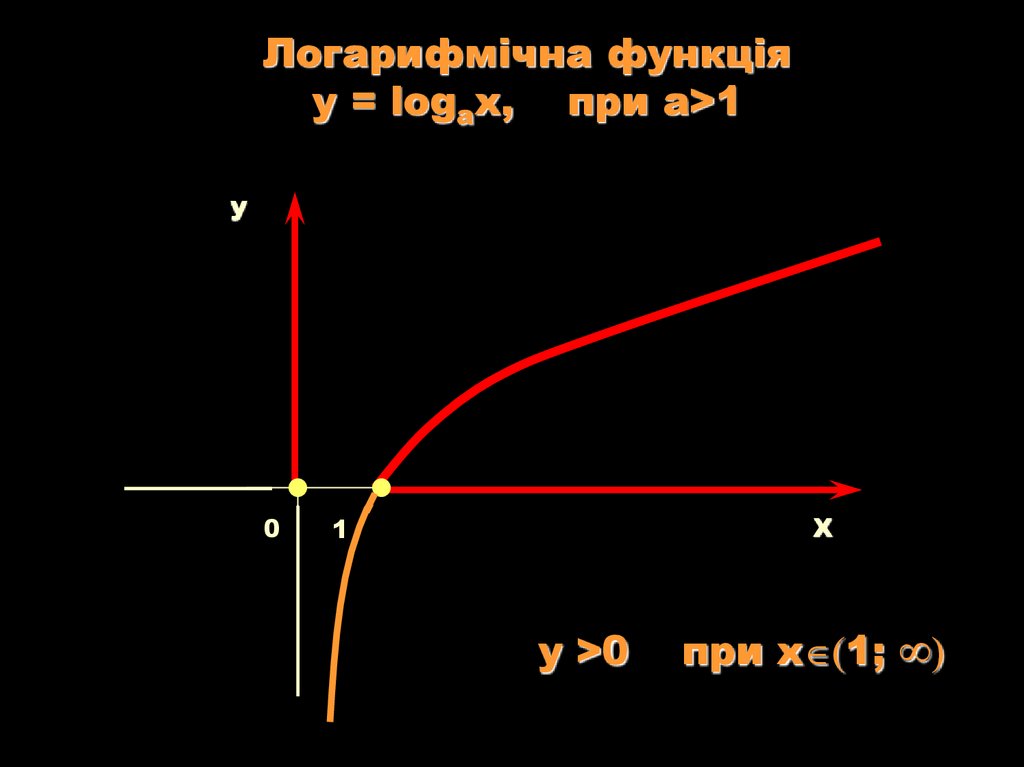
Логарифмічна функціяy = logаx, при a>1
У
0
Х
1
у >0
при х 1;
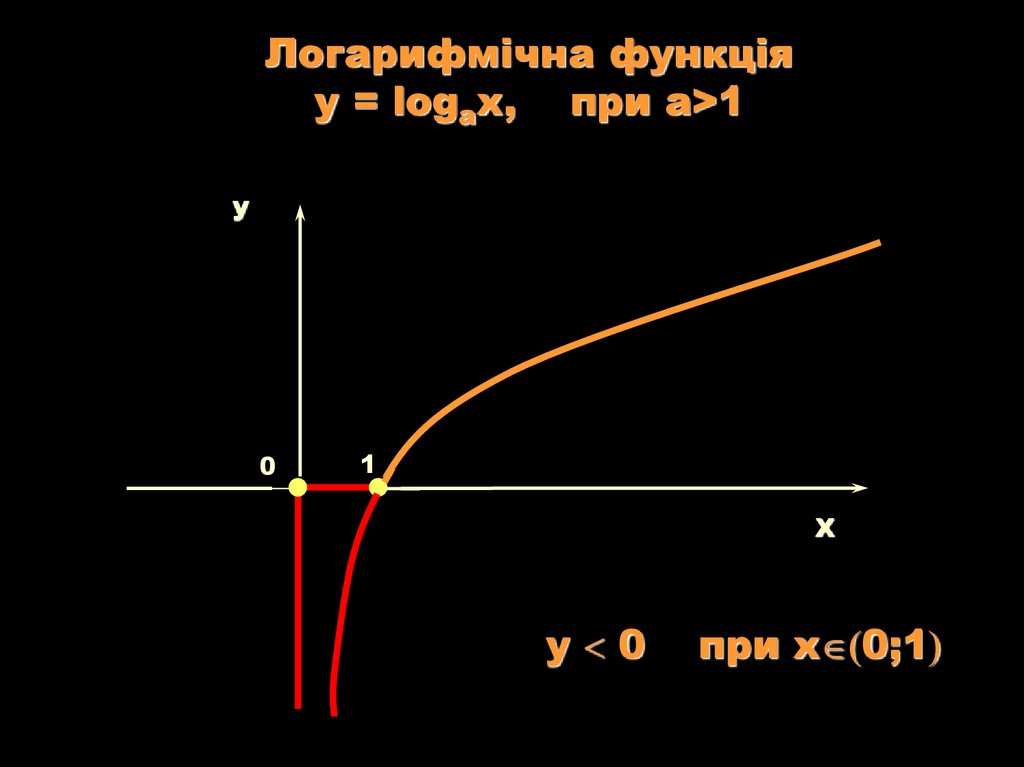
11.
Логарифмічна функціяy = logаx, при a>1
У
0
1
Х
у 0
при х 0;1
12.
Логарифмическая функцияy = logаx, при 0<a<1
У
у 0
0
1
при х 0;1
Х
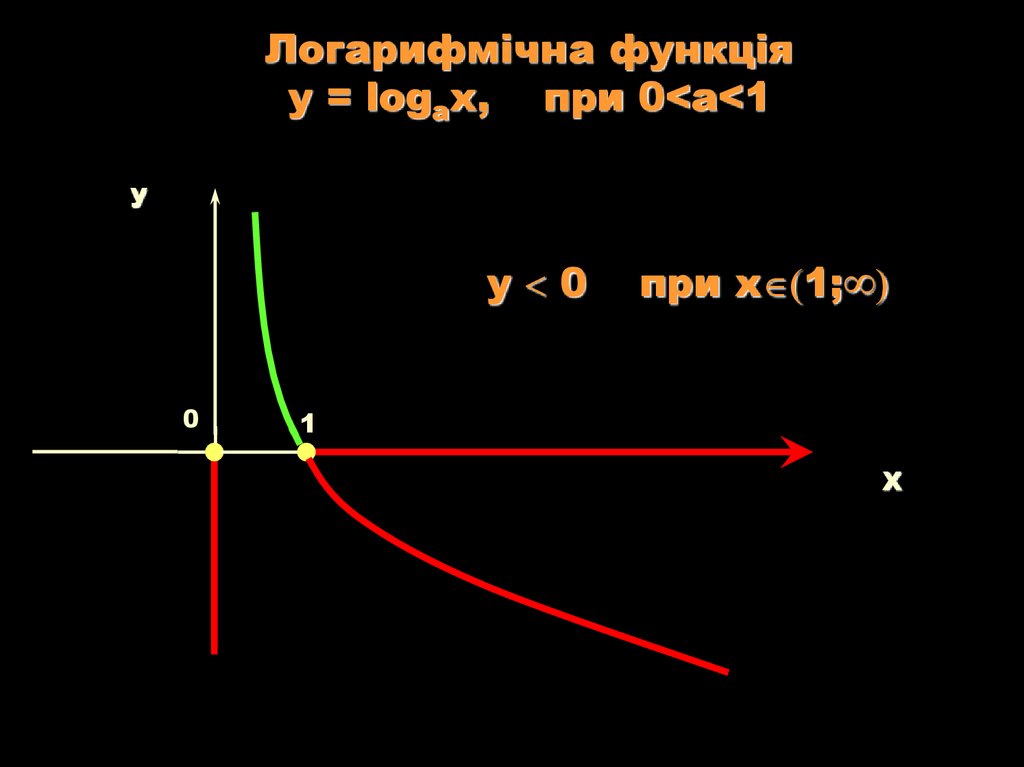
13.
Логарифмічна функціяy = logаx, при 0<a<1
У
у 0
0
при х 1;
1
Х
14.
Для проміжків знакосталості:y=logaх
0
0
a
х
1
a
х
1
a 1 и x 1
y 0
0 a 1 и 0 x 1
Якщо число і основа
логарифмічної функції
знаходяться по одну сторону
від 1 , то значення
логарифмічної функції цього
числа додатнє.
Якщо число і основа
логарифмічної функції
знаходяться по різні сторони від 1 , то значення
логарифмічної функції цього
числа від’ємнє.
0
a
1
х
0
x
1
a
a 1 и 0 x 1
y 0
0 a 1 и x 1
15.
Завдання.Визначте знак числа:Якщо число і основа
логарифма лежать
по одну сторону від 1,
то логарифм додатній;
Якщо число и основа
логарифма лежать
по різні сторони від 1,
то логарифм
від’ємний.
log 2 3 0
log 0,2 0,8 0
log 5 0,1 0
log 0,3 1,8 0
2 1,
3 1
0 0,2 1,
0 0,8 1
5 1,
0 0,1 1
0 0,3 1,
1,8 1
16.
Завдання. Який висновок можназробити відносно числа m, якщо:
log 1 m 0,5
m 1
1
0 1, 0,5 0
2
m 1
3 1, 1,5 0
2
log 3m 1,5
4
log 0,2m
3
0 m 1
log 2,4m 0,2
0 m 1 2,4 1, 0,2 0
0 0,2 1,
4
0
3
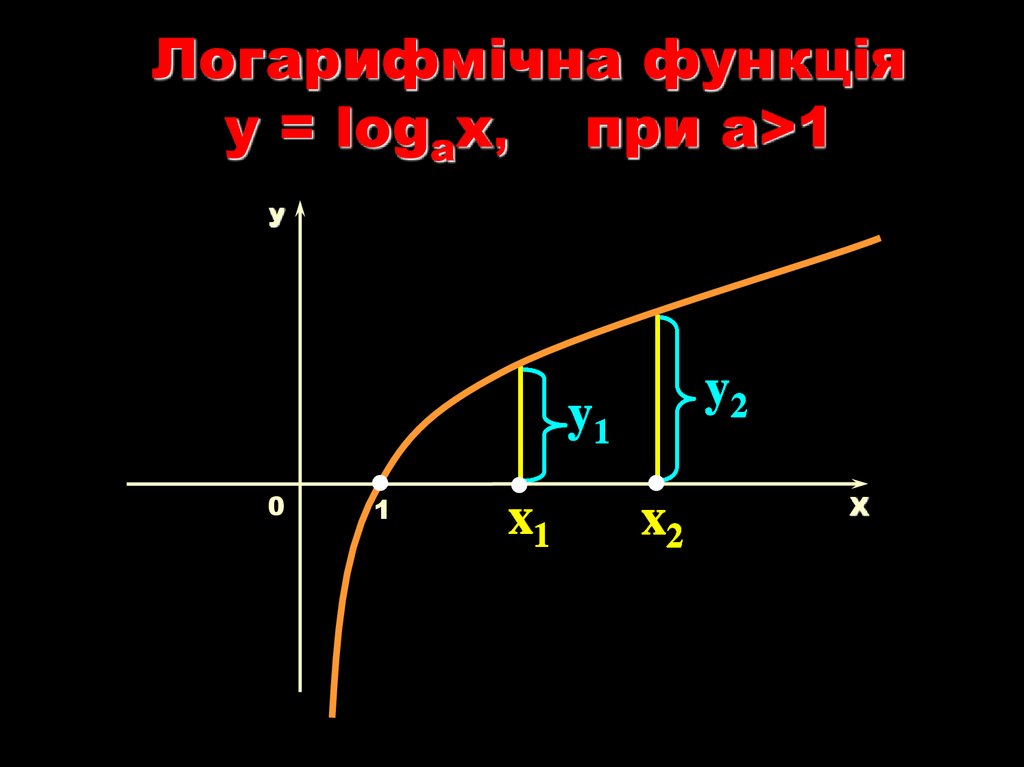
17.
Логарифмічна функціяy = logаx, при a>1
У
y2
y1
0
1
x1
x2
Х
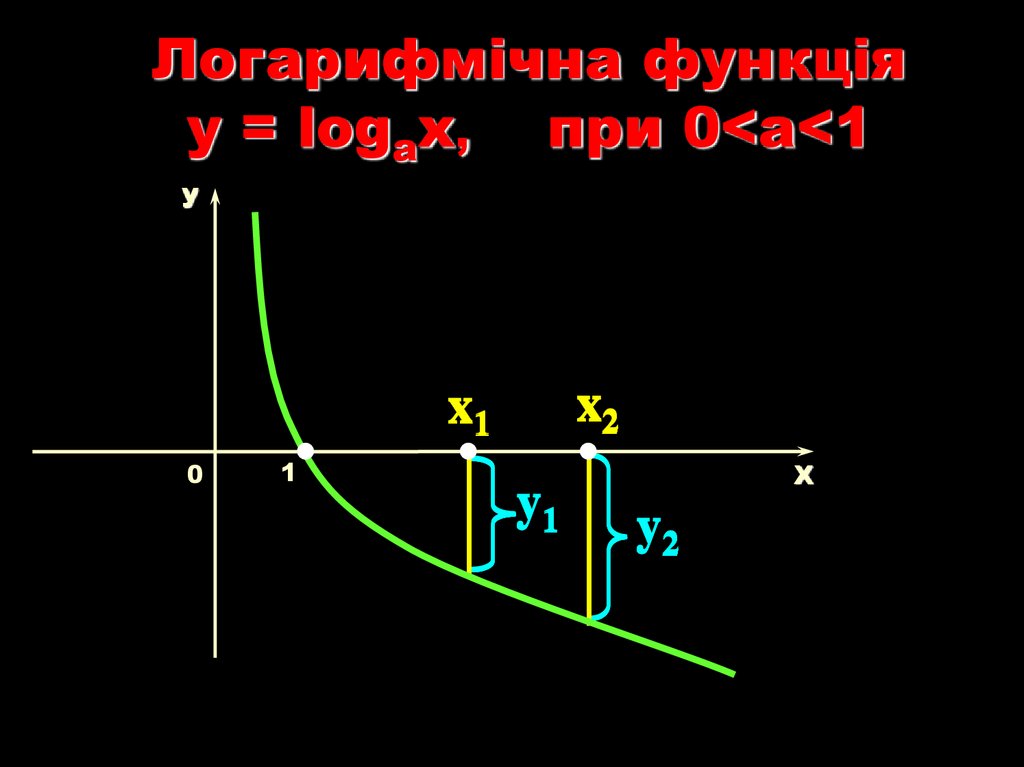
18.
Логарифмічна функціяy = logаx, при 0<a<1
У
x2
x1
0
1
y1
Х
y2
19.
Які з нижче перерахованих функцій єзростаючими, а які спадними?
y log 2 x
зростаюча,
2 1
спадна,
0 0,5 1
y lg x
зростаюча,
10 1
y lnx 2
зростаюча,
e 1
спадна,
0 0,7 1
y log 0,5 x
y log
2
x
4
0,7
20.
Завдання. Між числами m і n поставитизнак > або <, якщо відомо,що:
m n
1
0 1
2
log 8m log 8n
m n
8 1
log 2,5m log 2,5n
m n
2,5 1
log 0,2m log 0,2n
m n
0 0,2 1
log 1 m log 1 n
2
2
21.
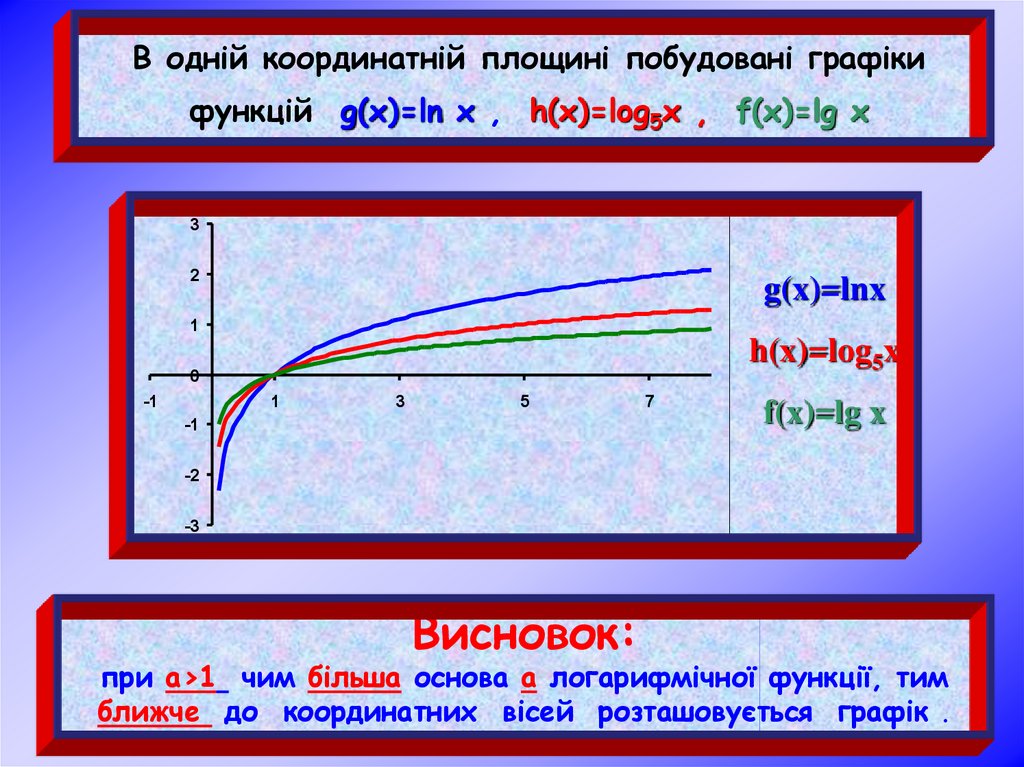
В одній координатній площині побудовані графікифункцій g(x)=ln x , h(x)=log5x , f(x)=lg x
3
2
g(x)=lnx
1
h(x)=log5x
0
-1
1
3
5
-1
7
f(x)=lg x
-2
-3
Висновок:
при а>1 чим більша основа а логарифмічної функції, тим
ближче до координатних вісей розташовується графік .
22.
В одній координатній площині побудовані графікифункцій
g(x)=log0,1x,
h(x)=log0,3x,
f(x)=log0,5x
4
3
2
1
g(x)=log0,1x
0
-1
-1
1
3
5
7
-2
h(x)=log0,3x
f(x)=log0,5x
-3
-4
Висновок:
при 0<а<1 чим більша основа а логарифмічної функції,тим
далі від вісей координат розташовується графік .













 Математика
Математика








