Диференціальне числення. Визначення функції ( лекція 1.1)

1. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ

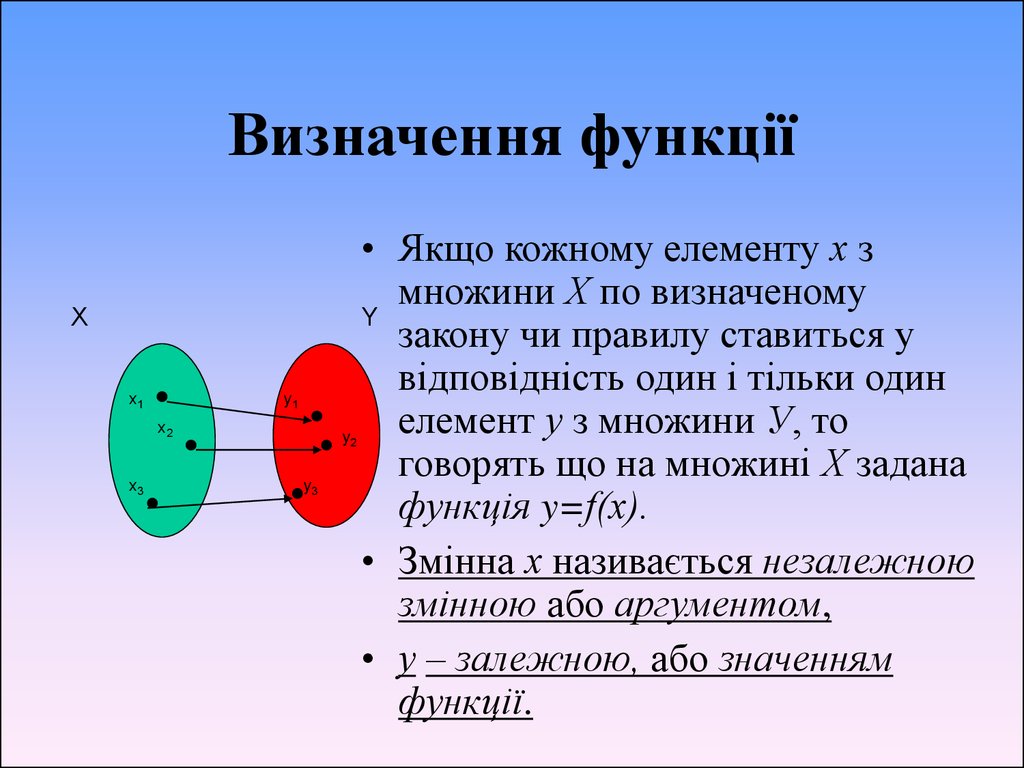
Лекція 1.1

2. Визначення функції

X
x1
y1
x2
x3
• Якщо кожному елементу х з
множини Х по визначеному
Y
закону чи правилу ставиться у
відповідність один і тільки один
елемент у з множини У, то
y
говорять що на множині Х задана
функція y=f(х).
• Змінна х називається незалежною
змінною або аргументом,
• у – залежною, або значенням
функції.
2
y3

3. Способи задання функції

• Табличний спосіб.
• Графічний спосіб .
• Аналітичний спосіб задання функції (за допомогою
формули). У загальному вигляді: y f (x.)
Наприклад:
n
y
x
• - степенева функція
,;
• - лінійна функція y ax b ;
• - показникова функція y a x ;
• - логарифмічна функція y log a x ;
• - тригонометричні функції:
y sin x ;
y cos x ;
y tgx;
y ctgx

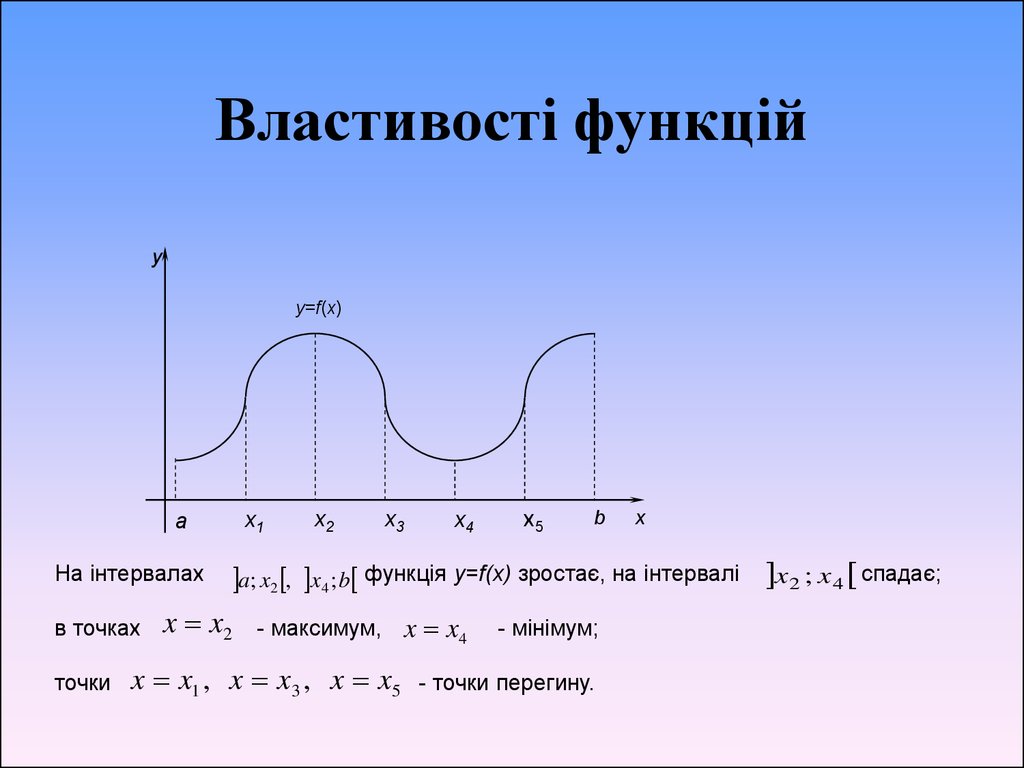
4. Властивості функцій

1.
Множина усіх значень Х називається областю визначення функції
D(f), а множина значень У, називають множиною значень функції
E(f).
2.
Функція , називається парною, якщо для будь-якого значення
аргументу х з області визначення функції виконується рівність:
f ( x) f ( x)
Функція , називається непарною, якщо для будь-якого значення х з
області визначення функції виконується рівність:
f ( x) f ( x)
3.
Функція називається монотонно зростаючою на всій області
визначення (чи на інтервалах), якщо для будь-якого значення х з
області визначення функції (чи з інтервалу) виконується нерівність
x1 x2 f ( x1 ) f ( x2 )
x
Якщо за тих же умов виконується нерівність: 1
тоді функція називається монотонно спадною.
x2 f ( x1 ) f ( x2 )

5. Властивості функцій

y
y=f(x)
а
На інтервалах
в точках
точки
x1
x2
x3
x4
x5
b
x
a; x2 , x4 ; b функція y=f(x) зростає, на інтервалі x 2 ; x 4 спадає;
x x2
- максимум, x x4
x x1 , x x3 , x x5
- мінімум;
- точки перегину.

6. Елементарні функції

Степенева функція
y
y x2
0
Степенева функція y=xn,
де n – парне натуральне
число.
y xn
y x3
y
x
0
Степенева функція y=xn,
де n – непарне натуральне
число.
x

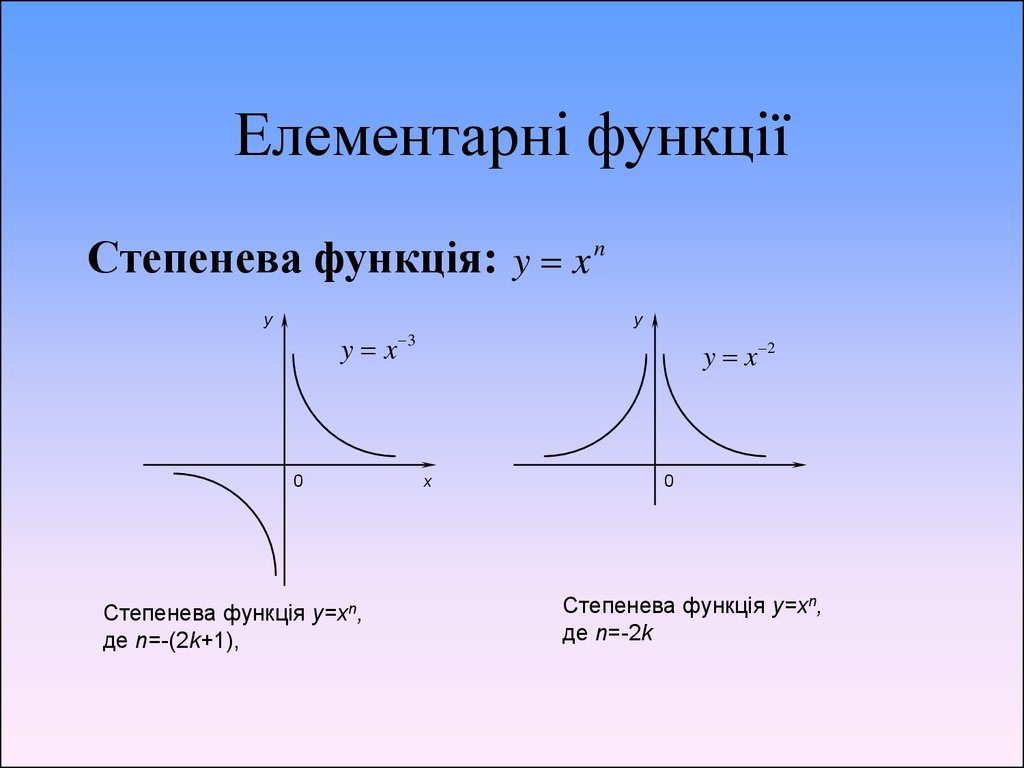
7. Елементарні функції

Степенева функція: y x n
y
y
y x
0
Степенева функція y=xn,
де n=-(2k+1),
3
y x 2
x
0
Степенева функція y=xn,
де n=-2k

8. Елементарні функції

Лінійна функція: y kx b , де k і b будь-які постійні числа.
(2)
y
(1)
y=kx+b
b
0
x
Графік функції у=kx+b перетинає вісь Ox в точці х=-k/a, вісь Oy в
точці y=b.
Два випадки: (1) a>0; (2) a<0.

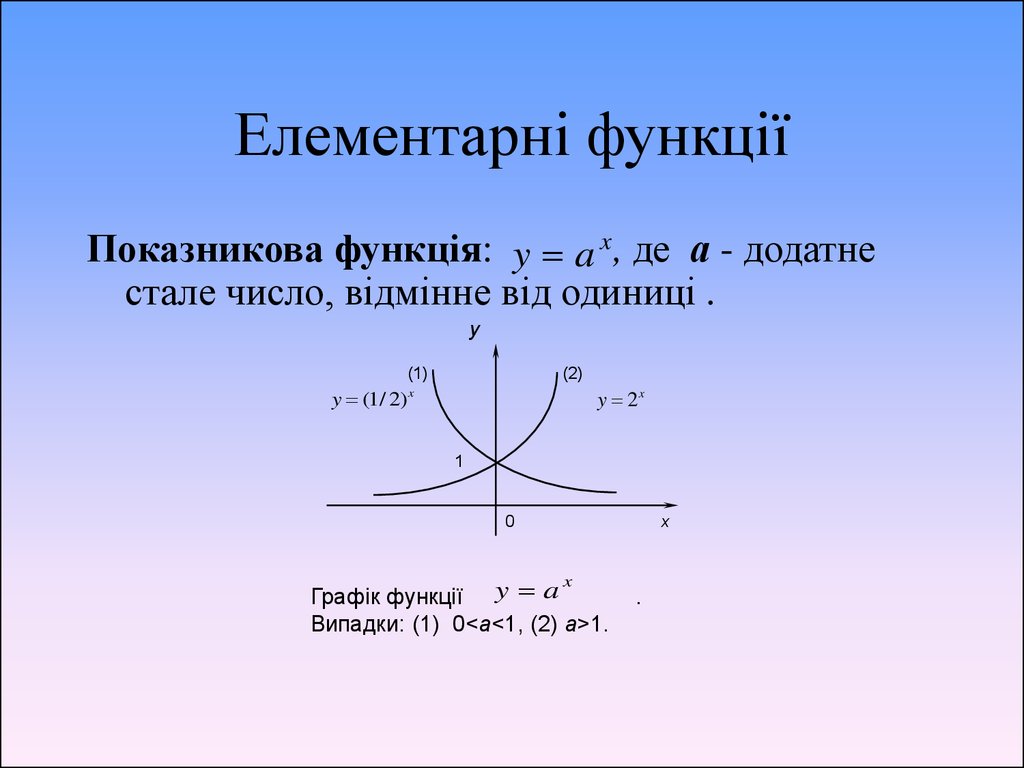
9. Елементарні функції

Показникова функція: y a x, де а - додатне
стале число, відмінне від одиниці .
y
(1)
y (1/ 2)
(2)
y 2x
x
1
0
x
Графік функції y a
Випадки: (1) 0<а<1, (2) a>1.
x
.

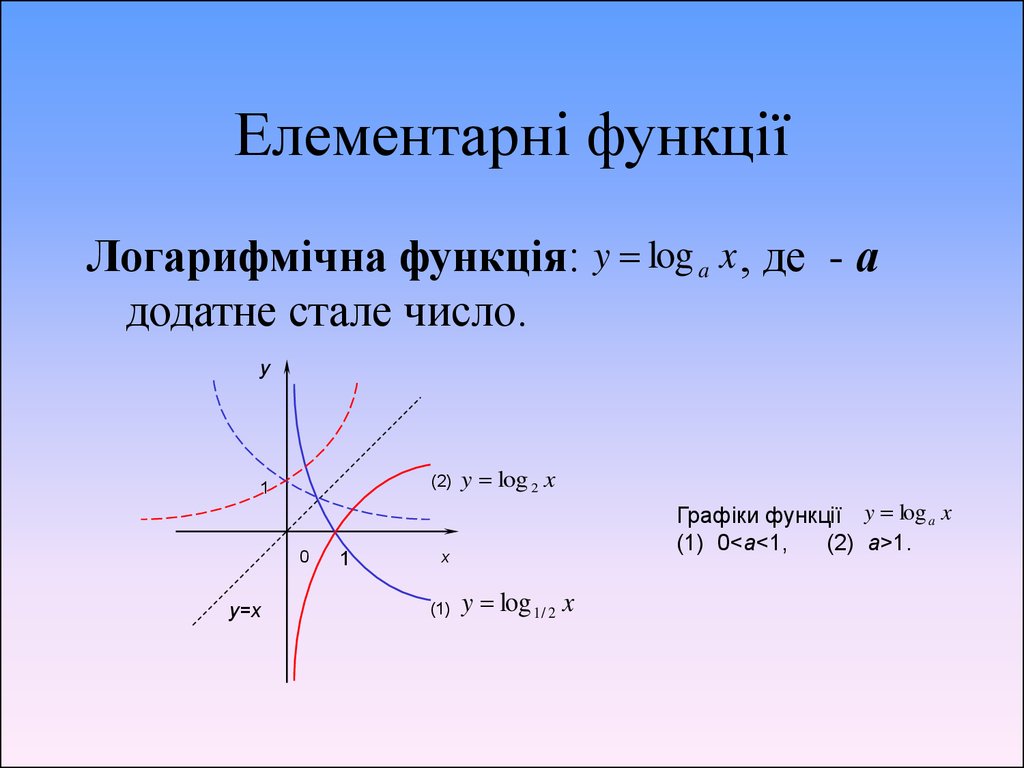
10. Елементарні функції

Логарифмічна функція: y log a x , де - а
додатне стале число.
y
(2)
1
0
y=x
1
y log 2 x
Графіки функції y log a x
(1) 0<a<1,
(2) a>1.
x
(1)
y log 1 / 2 x

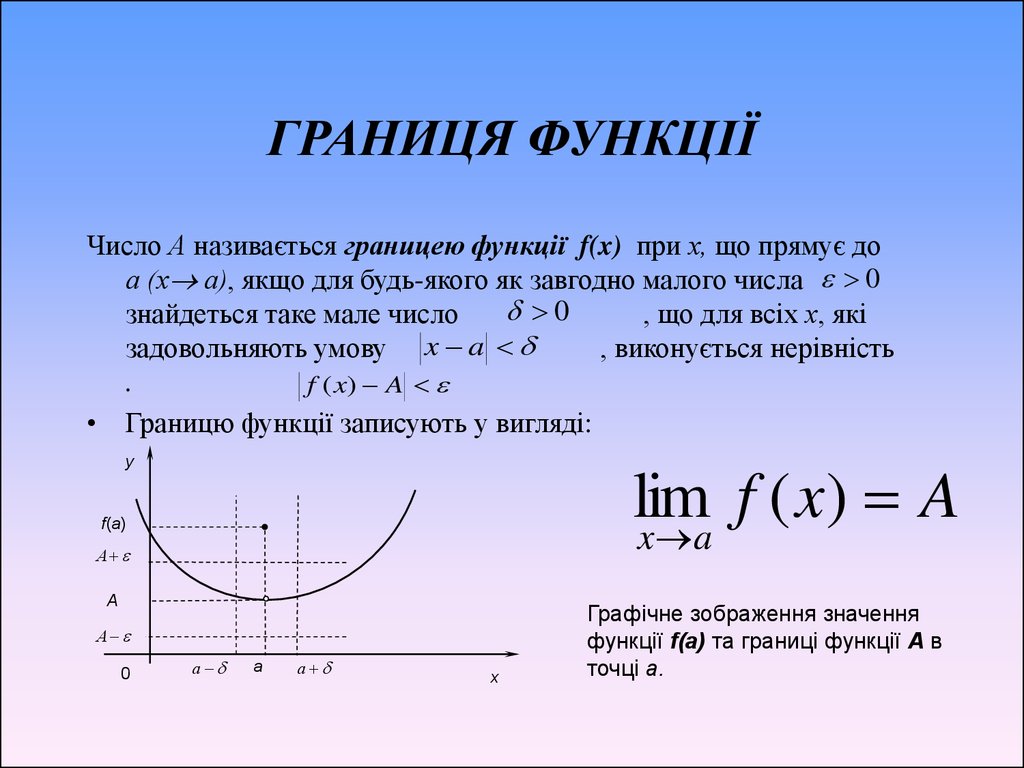
11. ГРАНИЦЯ ФУНКЦІЇ

Число А називається границею функції f(x) при х, що прямує до
а (х а), якщо для будь-якого як завгодно малого числа 0
0
знайдеться таке мале число
, що для всіх х, які
задовольняють умову x a
, виконується нерівність
.
f ( x) A
• Границю функції записують у вигляді:
lim
f
(
x
)
A
x a
y
f(а)
A
А
A
0
a
а
a
x
Графічне зображення значення
функції f(a) та границі функції A в
точці а.

12. Теореми про границі функції

1) lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x a
x a
x a
2) lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x a
x a
x a
f ( x)
f ( x) lim
x
a
3) lim
x a g ( x)
lim g ( x)
, (lim
g ( x) 0)
x a
x a
sin x
1
x 0
x
4) lim
x
1
5) lim 1
x
x
lim (1 x)
x 0
1
x
e 2,71828 ....

13. Приклади визначення границі функції

№1
( x 6)( x 2)
x 2 6 2 4
x 2 8x 12
62 8 6 12 0
lim
lim
lim 2
lim 2
( )
x 6 x 7 x 6
x 6 6 7 6 6
x
6
x
6
0
( x 6)( x 1)
x 1 6 1 5
№2
3 5
3
5
3 5
3 5
1
1
)
1
2
2
2
2
1
x 2 3x 5
x
x
x
x
x
x
lim
lim 2
lim
lim
x
x 3 x 2 x 6
x 2
x
2 6
2
6
2 6
2 6
x (3 2 )
3 2
3 2 3 2 3
x x
x x
x x
x 2 (1
№3
sin 5x
5 sin 5x
sin 5x
1
lim
5 lim
x 0 x cos x
x 0 5 x cos x
x 0
5x
cos x
sin 5x
1
5 lim
lim
5 1 1 5.
x 0
x 0 cos x
5x
lim