Похожие презентации:
Аксиомы стереометрии
1.
2.
- Что такое геометрия?Геометрия – наука о свойствах геометрических фигур
«Геометрия» - (греч.) – «землемерие»
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором
изучаются свойства фигур на плоскости.
- Основные понятия планиметрии?
Основные понятия планиметрии:
А
точка
а
прямая
3.
- раздел геометрии,в котором
изучаются свойства
фигур в
пространстве
4.
ПланиметрияСтереометрия
Изучает свойства
геометрических фигур
на плоскости
Изучает свойства фигур
в пространстве
В переводе с греческого
слово «геометрия»
означает «землемерие»
«гео» – по-гречески
земля, «метрео» –
мерить
Слово «стереометрия»
происходит от греческих
слов «стереос» объемный,
пространственный,
«метрео» – мерить
5.
Основные фигуры в пространстве:точка
прямая
плоскость
а
α
Обозначение:
a, b, с, d…, m,
n,…(или двумя
заглавными
латинскими)
Обозначение: А;
В; С; …; М;…
Обозначение: α, β, γ…
М
β
А
В
N
Р
Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β;
не лежащие в плоскости β.
2. Назовите прямые, лежащие в плоскости
β; не лежащие в плоскости β
6.
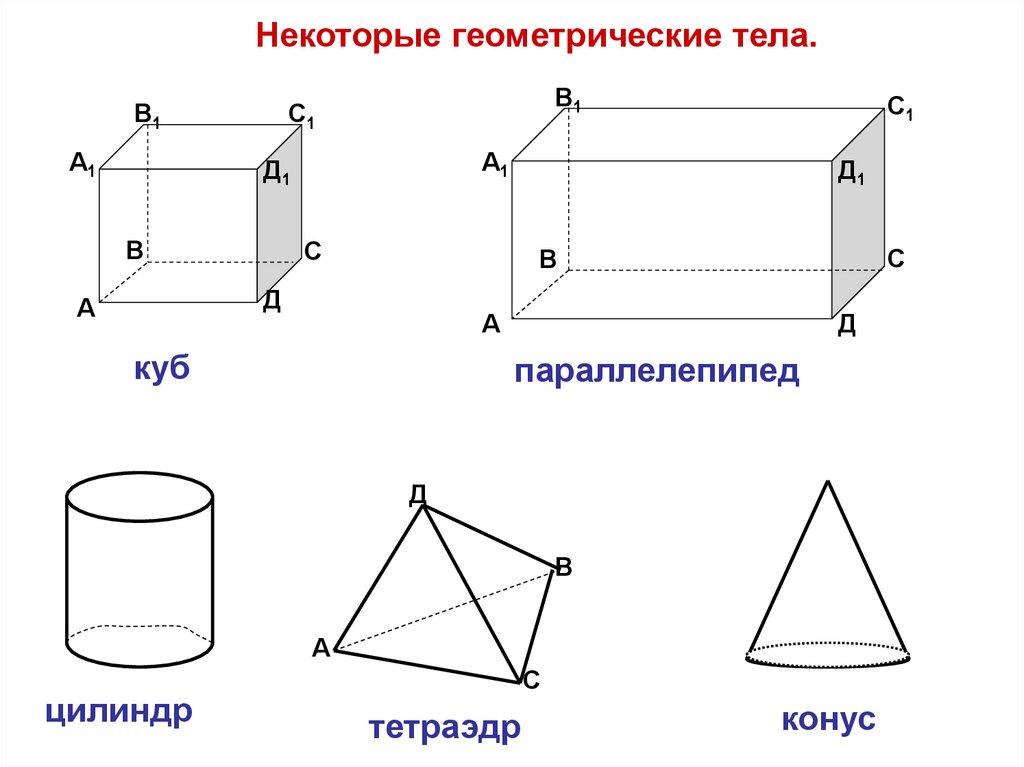
Некоторые геометрические тела.В1
А1
В1
С1
А1
Д1
В
Д1
С
С
В
Д
А
С1
А
куб
Д
параллелепипед
Д
В
А
цилиндр
С
тетраэдр
конус
7.
Назовите какие геометрические тела вам напоминают предметы,изображенные на этих рисунках:
8.
Стереометрия широко используется встроительном деле, архитектуре, машиностроении,
геодезии, во многих других областях науки и техники.
При
проектировании
этой машины
важно было получить такую форму, чтобы при
движении сопротивление воздуха было минимально.
9.
Оперный театр в СиднееДатский архитектор Йорн Утцон был
вдохновлён видом парусов.
10.
Эйфелева башняПариж, Марсово поле
Инженер Гюстав
Эйфель нашел
необычную форму для
своего проекта.
Эйфелева башня
весьма устройчива:
сильный ветер
отклоняет ее вершину
всего лишь на 10-12 см.
В жару от
неравномерного
нагревания
солнечными лучами
она может отклониться
на 18 см.
11.
18000 железных деталей скрепляются 2500000заклёпками
12.
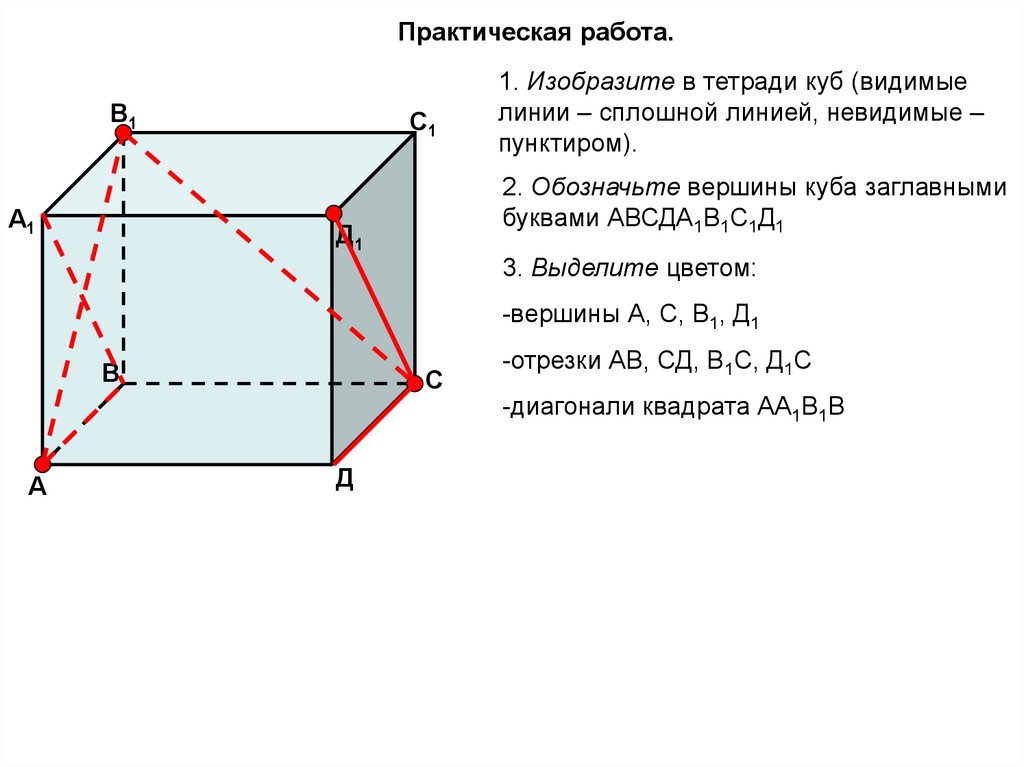
Практическая работа.В1
А1
С1
1. Изобразите в тетради куб (видимые
линии – сплошной линией, невидимые –
пунктиром).
2. Обозначьте вершины куба заглавными
буквами АВСДА1В1С1Д1
Д1
3. Выделите цветом:
-вершины А, С, В1, Д1
В
А
С
Д
-отрезки АВ, СД, В1С, Д1С
-диагонали квадрата АА1В1В
13.
- Что такое аксиома?Аксиома – это утверждение о свойствах
геометрических фигур, принимается в качестве
исходных положений, на основе которых доказываются
далее теоремы и вообще строится вся геометрия.
Аксиомы планиметрии:
- через любые две точки можно провести прямую и
притом только одну.
-из трех точек прямой одна, и только одна, лежит
между двумя другими.
-имеются по крайней мере три точки, не лежащие на
одной прямой…
14.
ВА
α
С
А1. Через любые три точки, не
лежащие на одной прямой, проходит
плоскость и притом только одна.
15.
Иллюстрации к аксиоме А1 из жизни.Для
видеокамеры,
фотосъемки
для других
приборов
часто
Табурет
с тремя ножками
всегдаиидеально
встанет
на пол
и
используют
штативУ–табурета
треногу. Три
ножки штатива
устойчиво
не будет качаться.
с четырьмя
ножками
бывают
расположатся
на любом полуесли
в помещениях,
проблемы с устойчивостью,
ножки стулана
неасфальте
одинаковые
или
прямоТабурет
на газоне
на улице,
наопирается
песке на пляже
в а
по длине.
качается,
т. е.
на триили
ножки,
траве
в лесу.
Три(четвертая
ножки штатива
всегда
четвертая
ножка
«точка»)
не найдут
лежит вплоскость.
плоскости
пола, а висит в воздухе.
16.
Если ножки стола не одинаковы по длине, то стол стоит на трехножках, т.е. опирается на три «точки», а конец четвертой ножки
(четвертая точка) не лежит в плоскости пола, а висит в воздухе.
17.
ВА
α
А2. Если две точки прямой лежат в
плоскости, то и все точки этой прямой лежат в
этой плоскости.
Говорят: прямая лежит в плоскости или плоскость
проходит через прямую.
18.
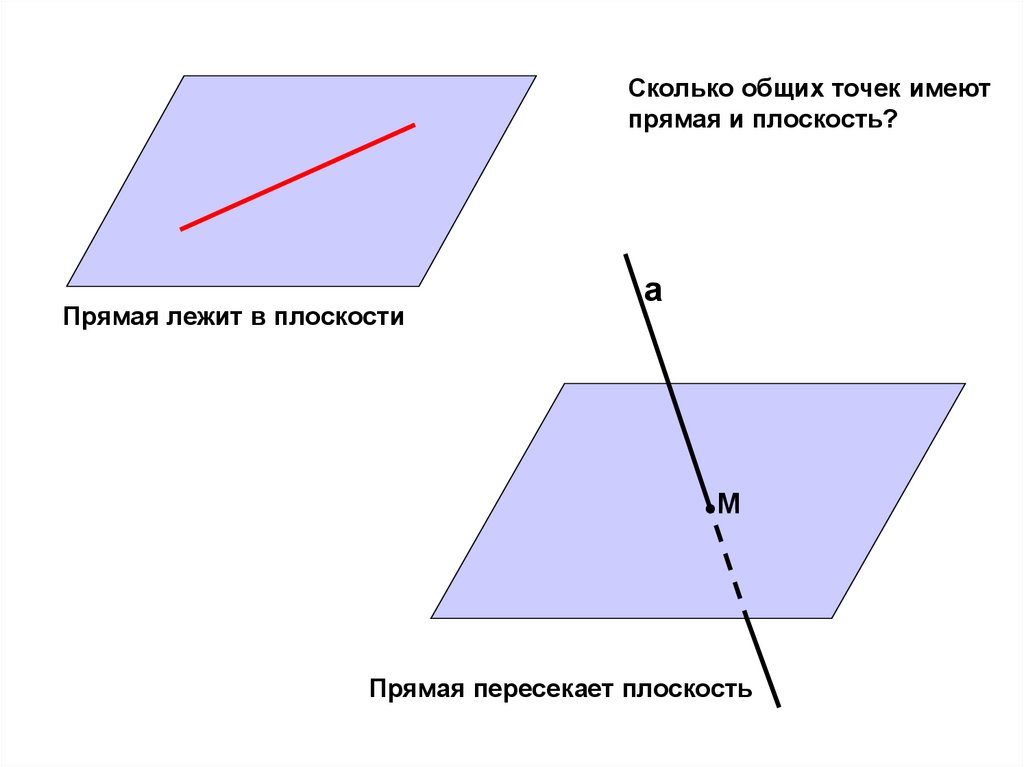
Сколько общих точек имеютпрямая и плоскость?
Прямая лежит в плоскости
а
М
Прямая пересекает плоскость
19.
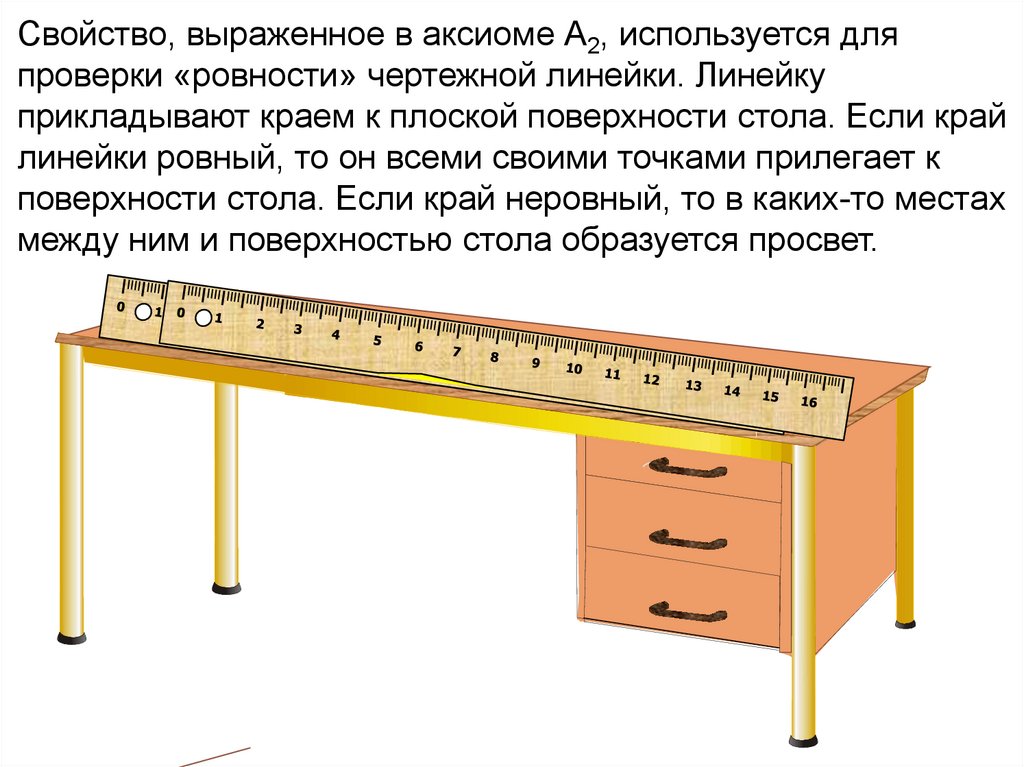
Свойство, выраженное в аксиоме А2, используется дляпроверки «ровности» чертежной линейки. Линейку
прикладывают краем к плоской поверхности стола. Если край
линейки ровный, то он всеми своими точками прилегает к
поверхности стола. Если край неровный, то в каких-то местах
между ним и поверхностью стола образуется просвет.
20.
βА
α
а
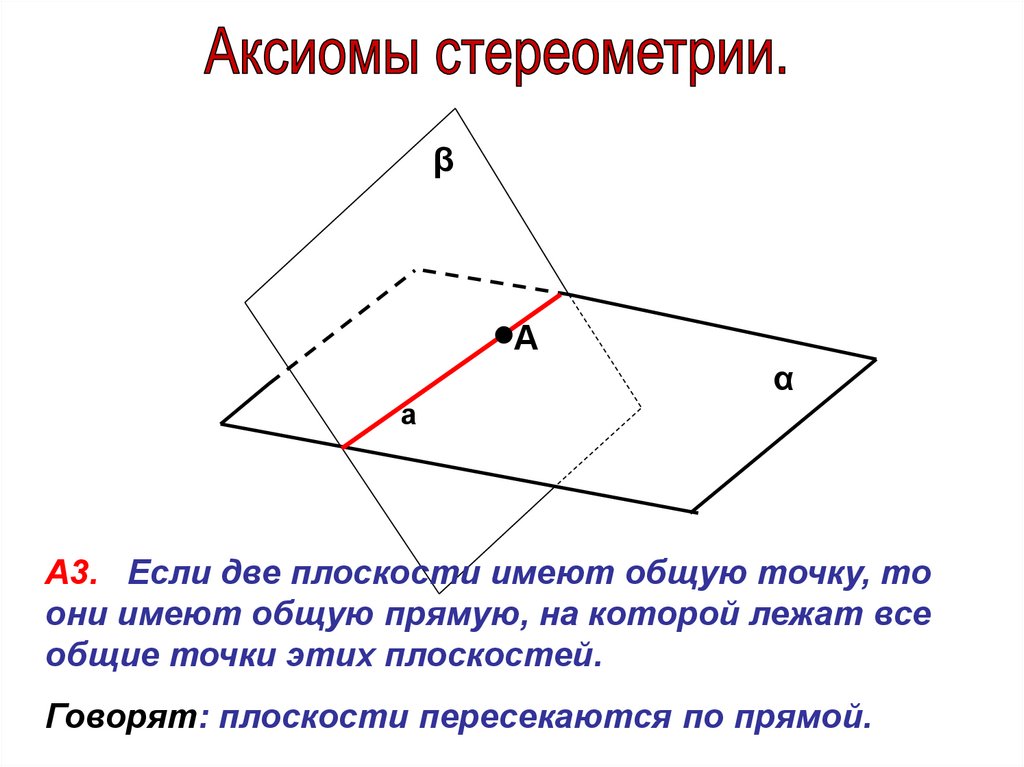
А3. Если две плоскости имеют общую точку, то
они имеют общую прямую, на которой лежат все
общие точки этих плоскостей.
Говорят: плоскости пересекаются по прямой.
21.
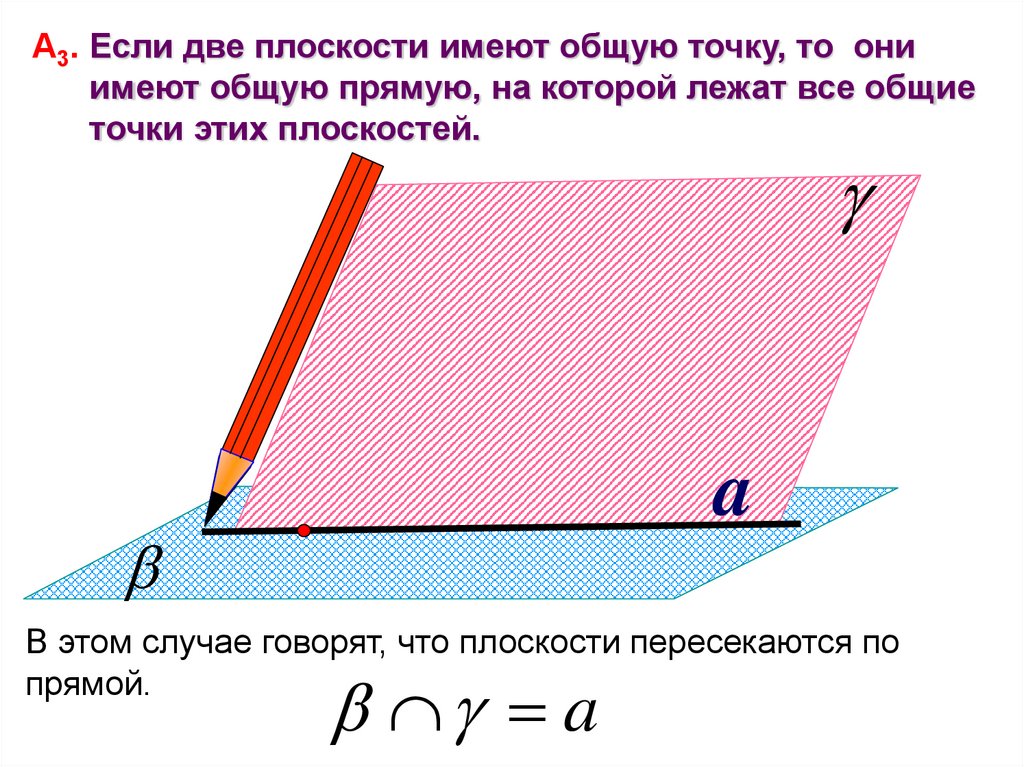
А3. Если две плоскости имеют общую точку, то ониимеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
В этом случае говорят, что плоскости пересекаются по
прямой.
a
22.
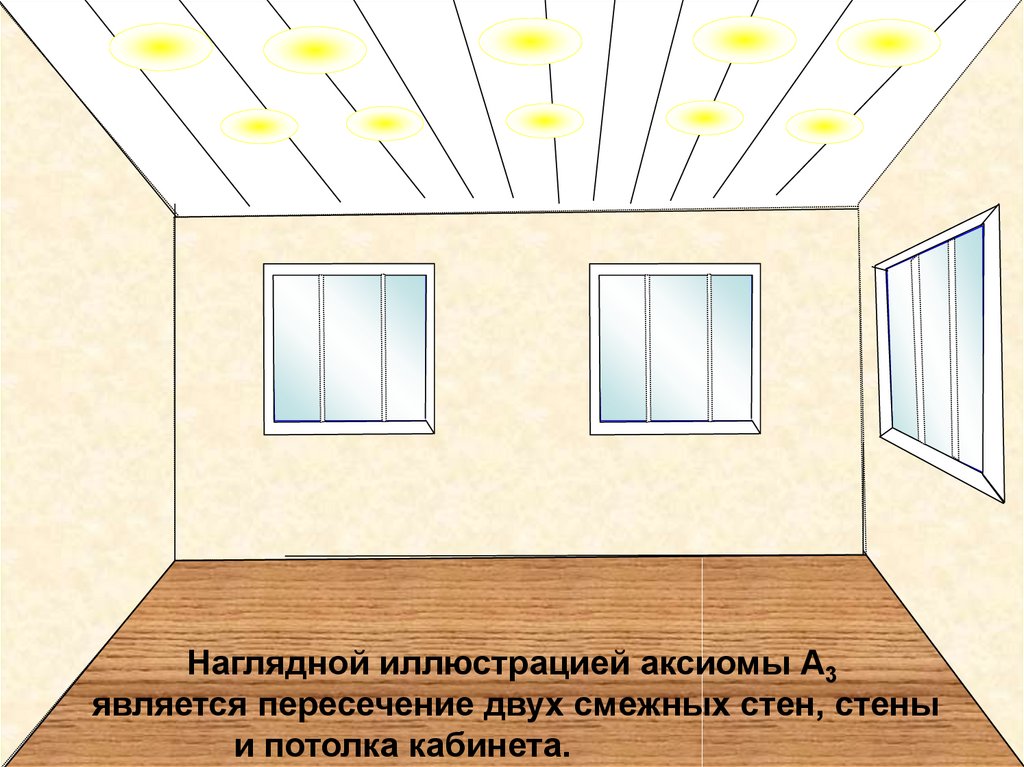
Наглядной иллюстрацией аксиомы А3является пересечение двух смежных стен, стены
и потолка кабинета.
23.
CB
A
B a
A
А 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 2.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 3.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.
24.
25.
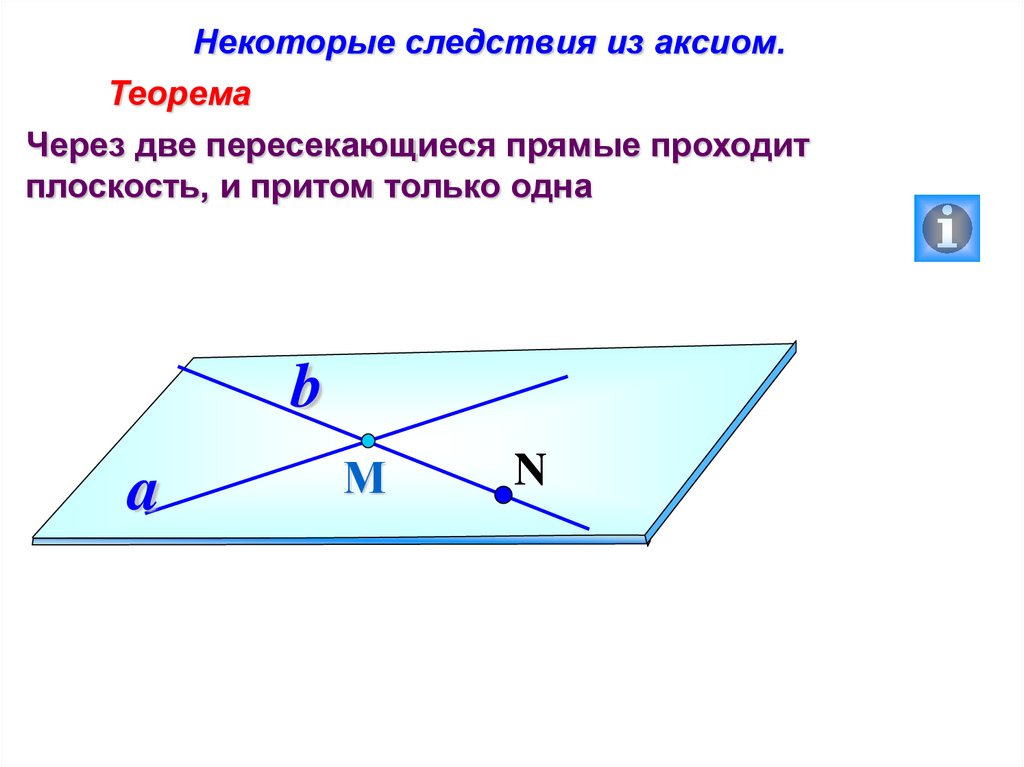
Некоторые следствия из аксиом.Теорема
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М
26.
Некоторые следствия из аксиом:Теорема 1. Через прямую и не лежащую на ней точку
проходит плоскость и притом только одна.
Дано:
α
О
Доказать:
(а, М) с α
α- единственная
Р
а
а, М ¢ а
М
Доказательство :
1. Р, О с а; {Р,О,М} ¢ а
По аксиоме А1: через точки Р, О, М проходит плоскость .
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и
вся прямая принадлежит этой плоскости, т.е. (а, М) с α
2. Любая плоскость проходящая через прямую а и точку М
проходит через точки Р, О, и М, значит по аксиоме А1 она –
единственная. Ч.т.д.
27.
Некоторые следствия из аксиом.Теорема
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N
28.
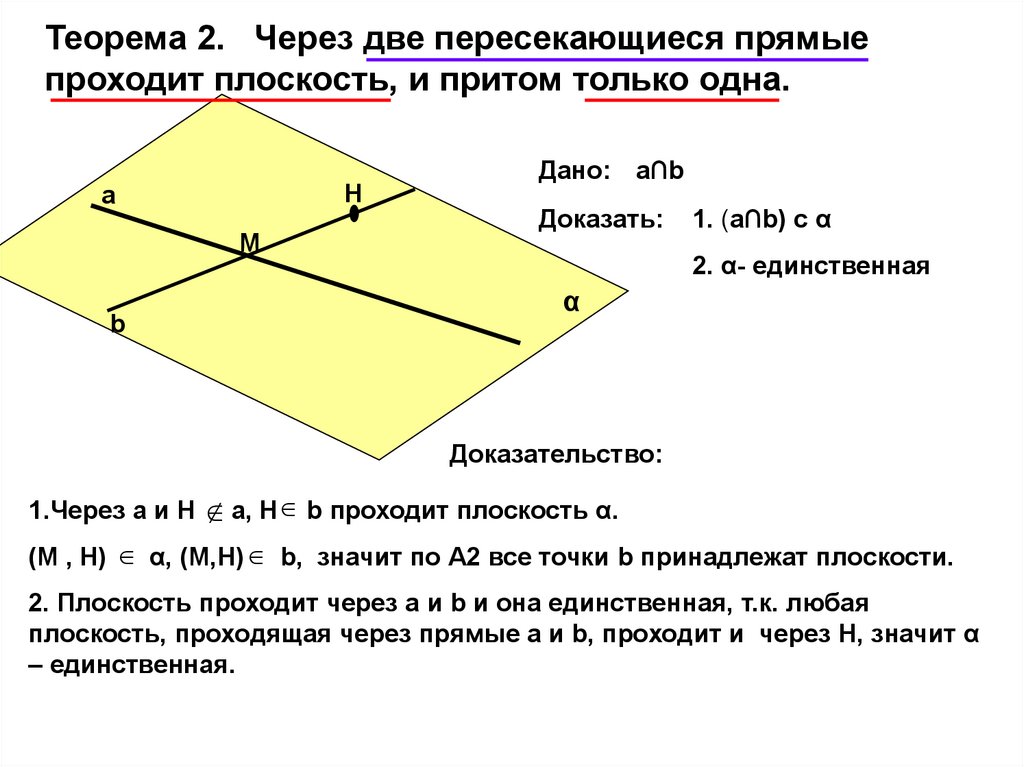
Теорема 2. Через две пересекающиеся прямыепроходит плоскость, и притом только одна.
Н
а
М
b
Дано: а∩b
Доказать:
1. (а∩b) с α
2. α- единственная
α
Доказательство:
1.Через а и Н
а, Н b проходит плоскость α.
(М , Н) α, (М,Н) b, значит по А2 все точки b принадлежат плоскости.
2. Плоскость проходит через а и b и она единственная, т.к. любая
плоскость, проходящая через прямые а и b, проходит и через Н, значит α
– единственная.
29.
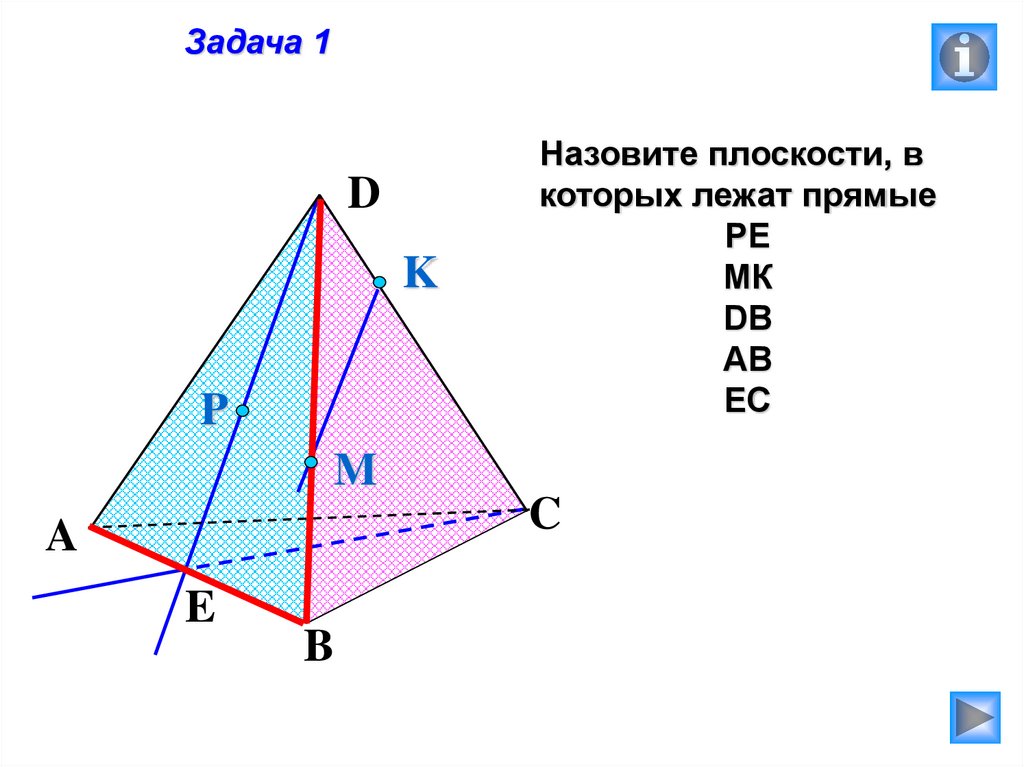
Задача 1D
K
P
Назовите плоскости, в
которых лежат прямые
РЕ
МК
DB
AB
EC
M
C
A
E
B
30.
Задача 2Назовите
D
K
P
M
точки пересечения
прямой DK с
плоскостью АВС,
прямой СЕ с
плоскостью АDB.
C
A
E
B
31.
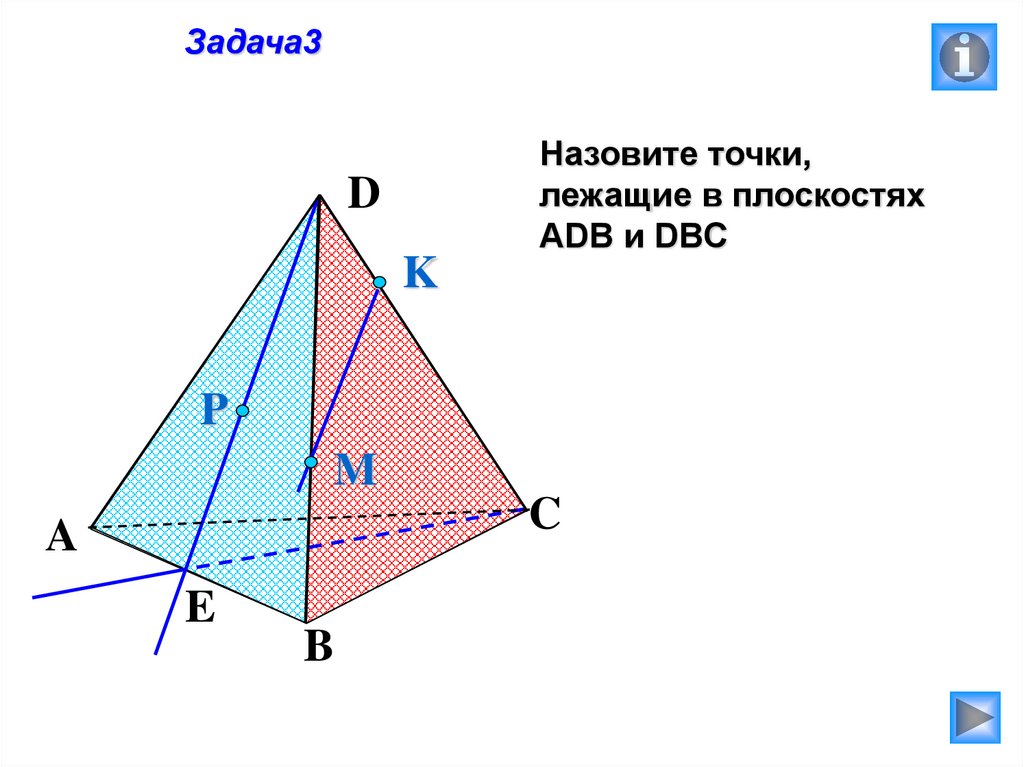
Задача3Назовите точки,
лежащие в плоскостях
АDB и DBC
D
K
P
M
C
A
E
B
32.
Задача4D
K
Назовите прямые по
которым пересекаются
плоскости
АВС и DCB
ABD и CDA
PDC и ABC
P
M
C
A
E
B
33.
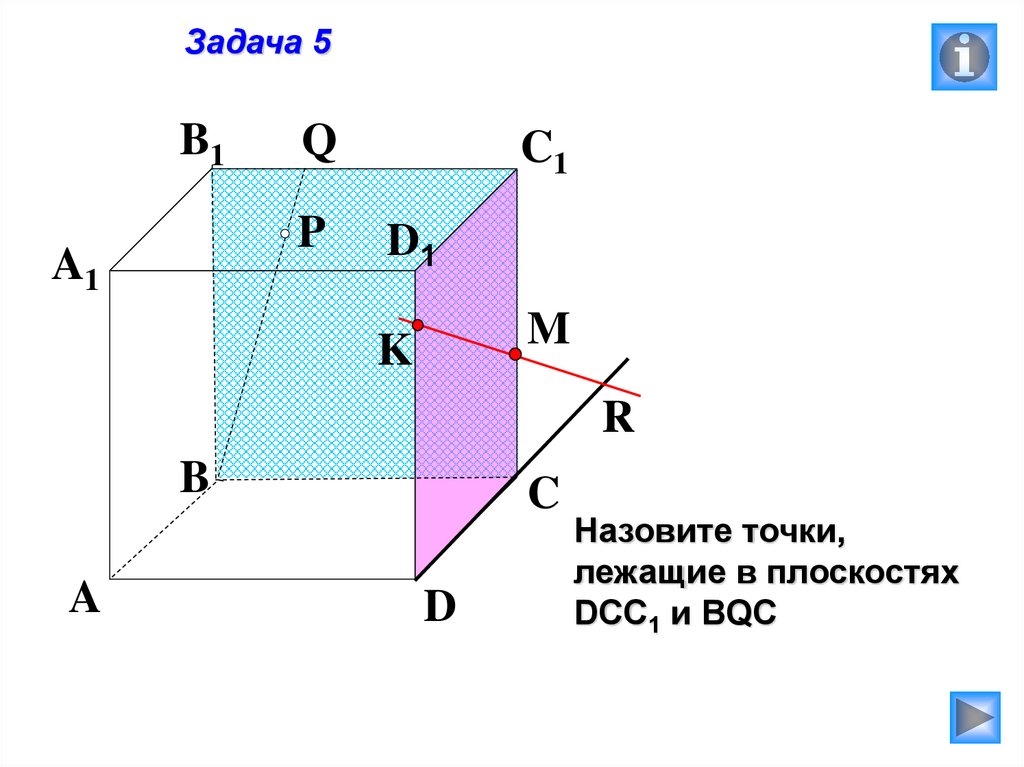
Задача 5B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
Назовите точки,
лежащие в плоскостях
DCC1 и BQC
34.
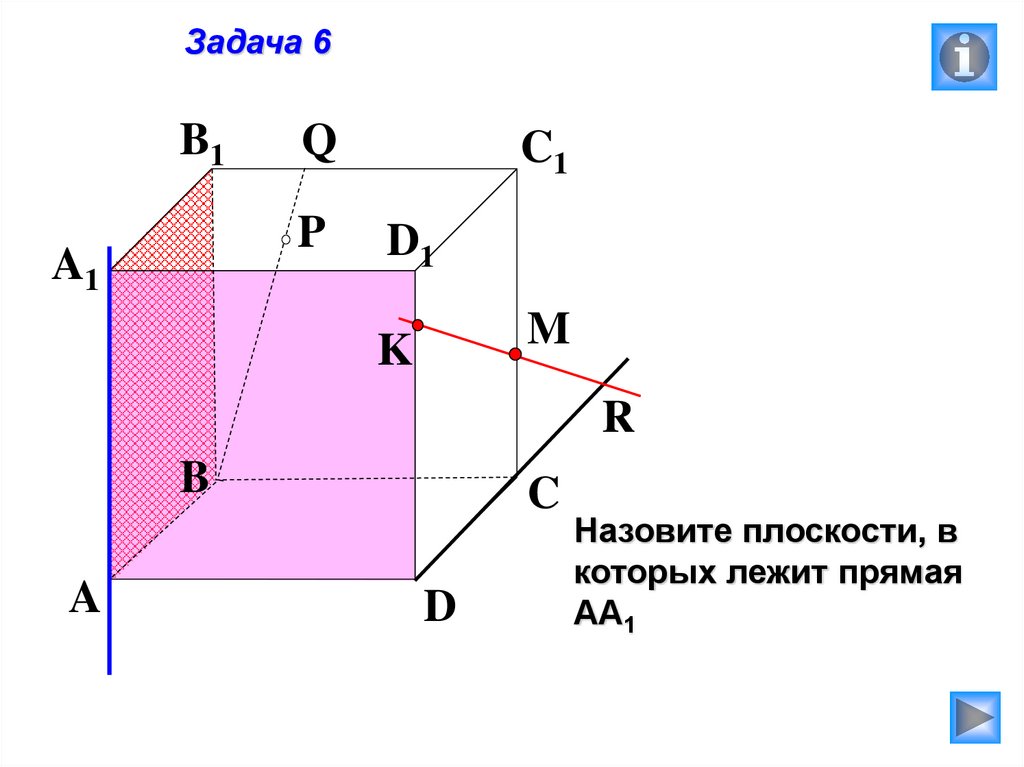
Задача 6B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
Назовите плоскости, в
которых лежит прямая
АА1
35.
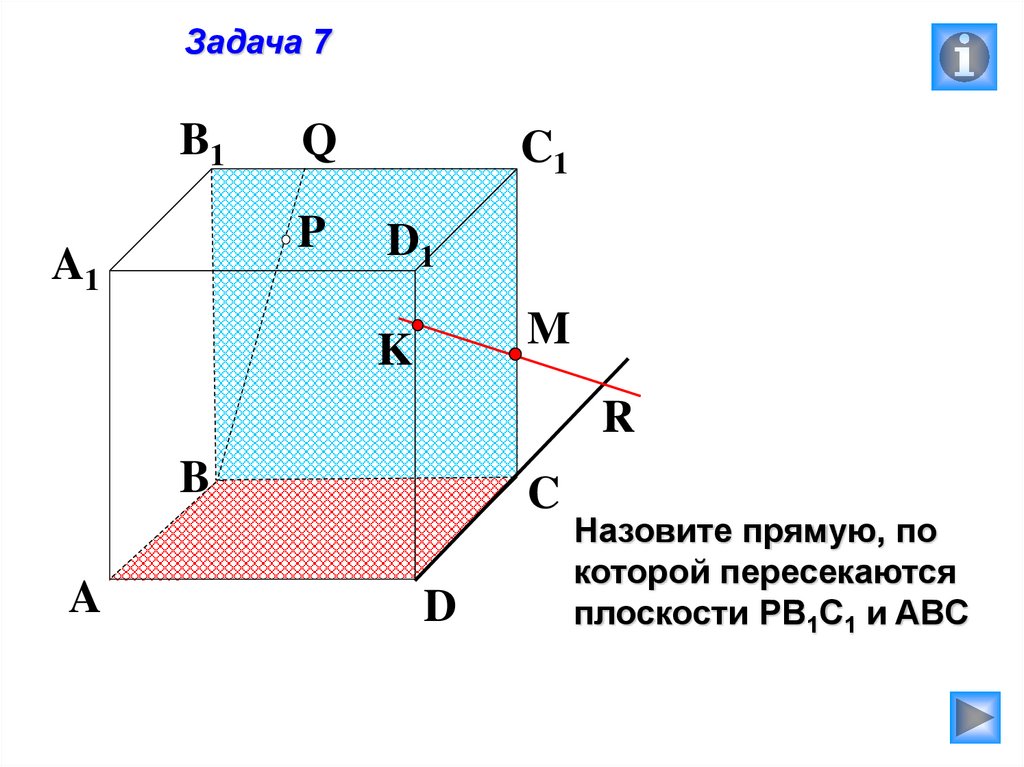
Задача 7B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
Назовите прямую, по
которой пересекаются
плоскости PВ1C1 и ABC
36.
Задача 8B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
Назовите точки
пересечения прямых
МК и DC,
В1С1 и ВР
С1М и DC
37.
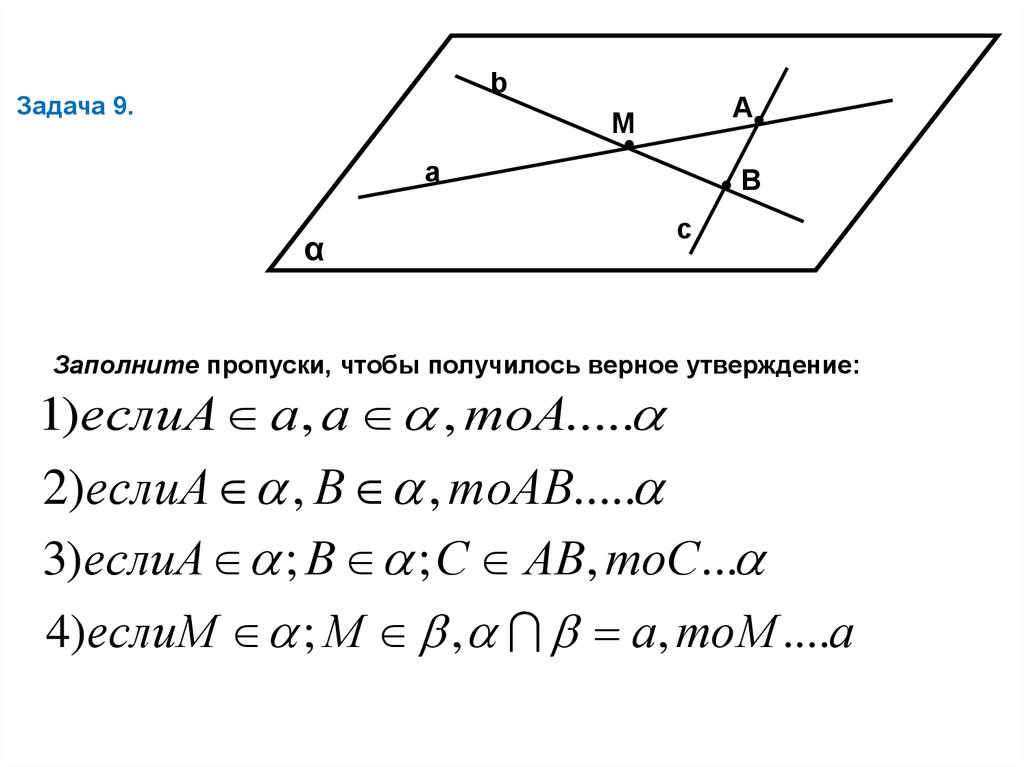
bЗадача 9.
А
М
а
α
В
c
Заполните пропуски, чтобы получилось верное утверждение:
1)еслиА а, а , тоА.....
2)еслиА , В , тоАВ.....
3)еслиА ; В ; С АВ, тоС...
4)еслиМ ; М , а, тоМ ....а






















 Математика
Математика








