Похожие презентации:
Уравнение Шредингера
1. Уравнение Шредингера для стационарных состояний
Если силовое поле не меняется стечением времени (поле
стационарно)
U U ( x, y, z ) E const
Решение уравнения Шредингера
можно переписать
( x, y, z, t ) ( x, y, z )e
i t
2.
2i t
i t
e U e
2m
i t
i ( i )e
E
t
2
U E 0
2m
Уравнение Шредингера для стационарных состояний
3.
Решение уравнения Шредингераимеет смысл только при
определенном наборе значений
энергии E – собственные значения,
соответствующие решения –
собственные функции
4. Движение свободной частицы
U ( x, y , z ) 02
U E 0
2m
2
E 0
2m
5.
Рассмотрим одномерный случайAe
ikx
d
d
ikx
2 Ae ik
dx
dx
2
Ae (ik )
ikx
2
k
2
6.
2k
E 0
2m
2 2
2 Px
k
k
E
2m
2
Px – может принимать любые значения
2
P
E
2m
– может принимать любые значения,
энергетический спектр непрерывный
7.
Найдем плотность вероятностиобнаружения частицы в некоторой
точке пространства
( x, t ) ( x)e
i ( t kx )
Ae
i t
ikx i t
Ae e
i ( t kx )
* ( x, t ) Ae
i ( t kx )
i ( t kx )
2
* Ae
Ae
A
вероятность обнаружения свободной частицы
не зависит от ее положения в пространстве
и везде одинакова
8. Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками
9.
UU , x 0, x
U 0,
0
ℓ
0 x
x
10.
2U E 0
2m
U 0, 0 x
( x 0) ( x ) 0,
Так как частица не проникает за границы ямы
d
2 E 0
2m dx
2
2
11.
d2
k
0
2
dx
2
x 0
2mE
k 2
2
(0) A sin 0 B cos 0
0 B 0
B 0
( x) A sin kx
12.
( ) A sin k 0x
sin k 0 k n k n
2mE
2
2 2
k 2
2mE n
2
2
2
2 2
n
En
, n 1,2,3...
2
2m
-собственные значения энергии
13.
-энергетические уровни имеют дискретныезначения – квантуются
n – главное квантовое число
( x) A sin
n
x
- постоянная А ищется из условия
нормировки
2
(
x
)
dx
1
0
14.
Asin
(
2
2
n
x)dx 1
0
2
2 n
A sin ( x)dx
0
2 n
2 1
A (1 cos
x)dx
2
0
1
1
2 n
2 n
A (
(sin
sin
0))
2
2 2 n
2
2 1
A
A 1
2
2
15.
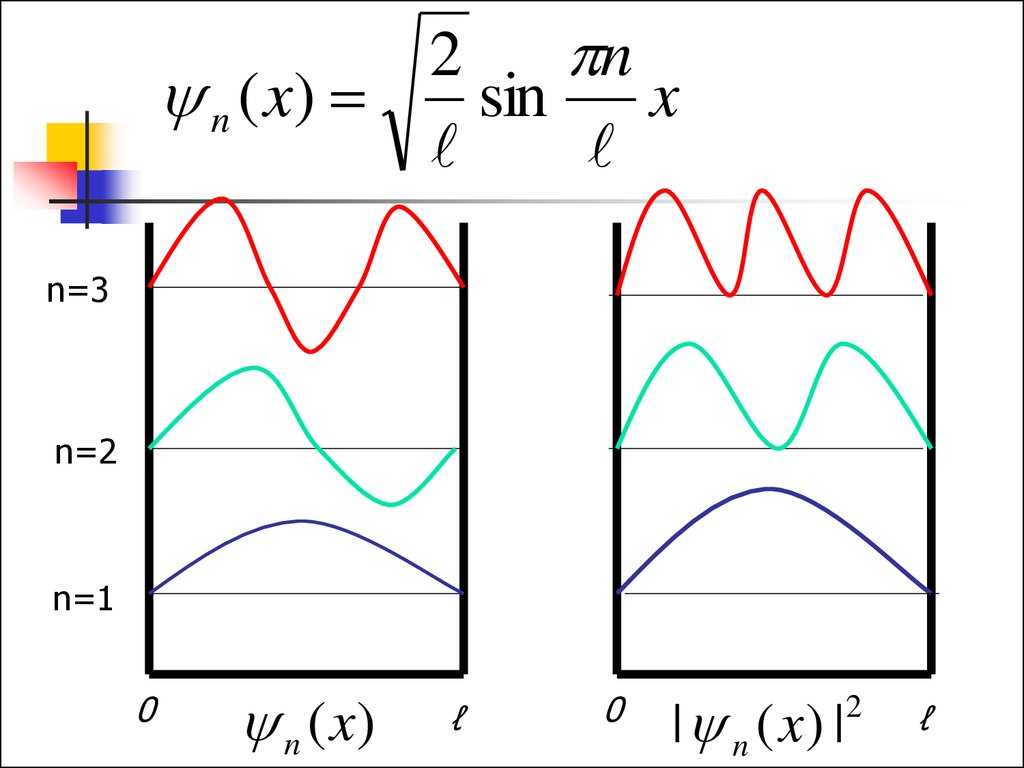
2n
n ( x)
sin
x
n=3
n=2
n=1
0
n (x)
ℓ
0
| n ( x) |
2
ℓ
16.
Найдем расстояние между соседнимиэнергетическими уровнями
En En 1 En
(n 1)
n
2
2
2m
2m
2
2
(
2
n
1
)
2
2m
2
2
2
2
2
2
17.
En 1En
n
-чем выше уровень энергии,
тем ближе они находятся друг к другу
18. Пример. Свободный электрон в металле
Размер потенциальной ямы – размеробразца - ℓ =10-2 м
E n
(
2
n
1
)
2
2m
2
34
2
(1,05 10 ) (3,14)
(2n 1)
31
4
2 9,1 10 10
10
33
n
2
Дж
2
Спектр можно считать
непрерывным
19. Пример. Электрон в атоме
размер атома - ℓ =10-10 мE n
(
2
n
1
)
2
2m
2
34
2
(1,05 10 ) (3,14)
(2n 1)
31
20
2 9,1 10 10
10
17
n
2
2
Дж 100n эВ
Спектр дискретный
20. ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ БПАРЬЕР
21.
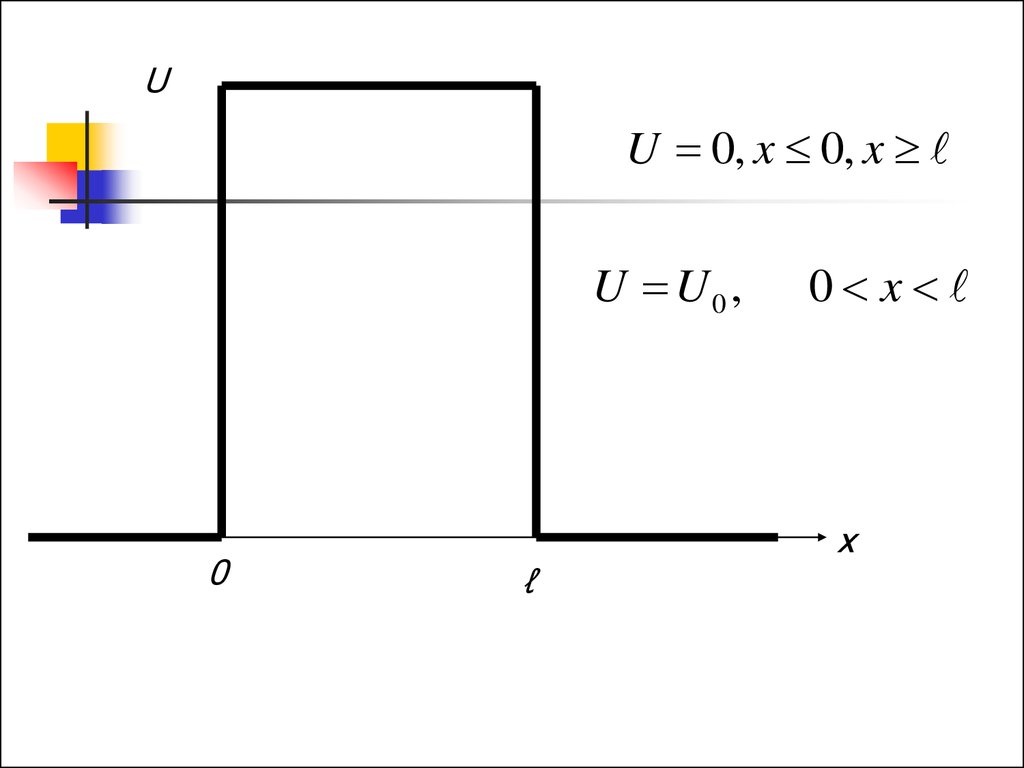
UU 0, x 0, x
U U0 ,
0
ℓ
0 x
x
22.
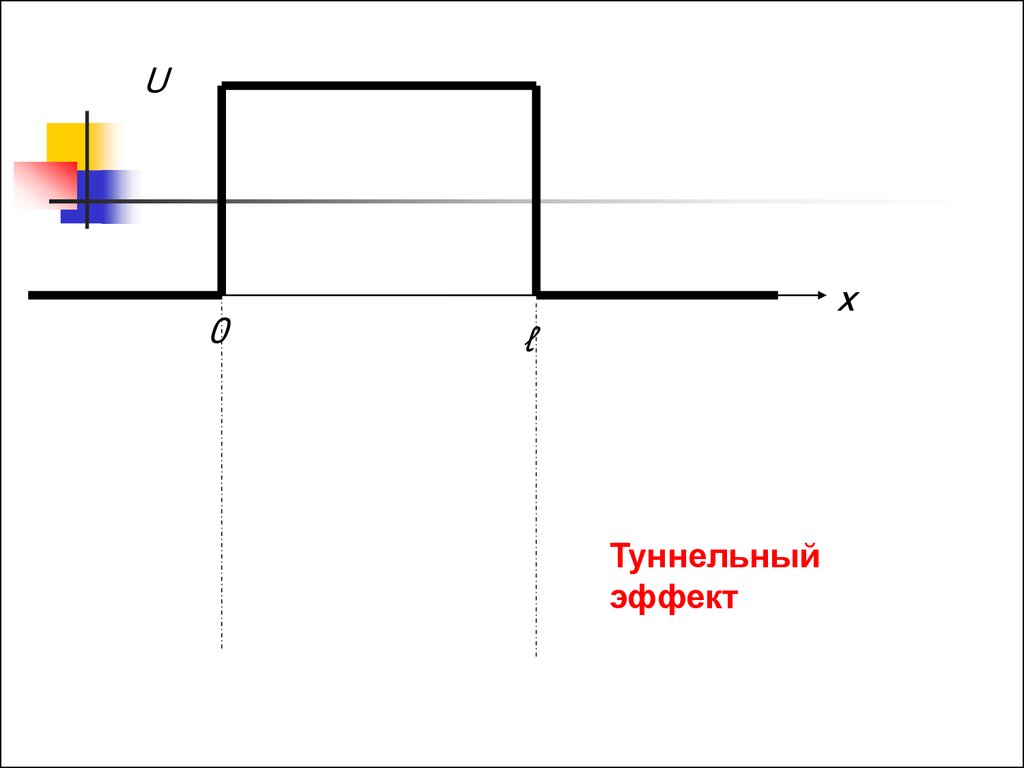
U0
x
ℓ
Туннельный
эффект
23.
В классическом случае, когда энергиячастицы меньше высоты потенциального
барьера она отразится от него
В квантовой механике – может проникнуть
через барьер – ТУННЕЛЬНЫЙ ЭФФЕКТ
В классическом случае, когда энергия
частицы больше высоты потенциального
барьера она беспрепятственно пролетит
над ним
В квантовой механике – может отразиться
от барьера – есть такая вероятность
24. КВАНТОВЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Система, у которой потенциальнаяэнергия имеет вид
m 0 x
U ( x)
2
2
0
2
- Собственная частота осциллятора
25.
Уравнение Шредингераm 0 x
d
E
0
2
2m dx
2
1
E ( n ) 0
2
2
2
2
2
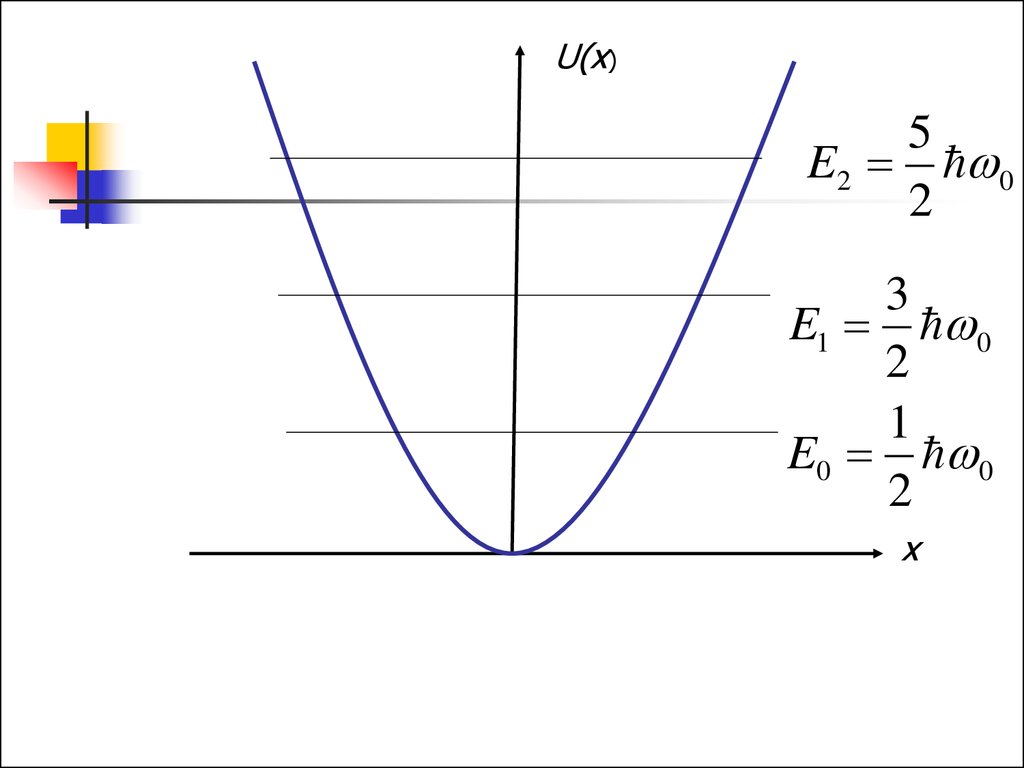
26.
U(x)5
E2 0
2
3
E1 0
2
1
E0 0
2
x
27.
Существует минимально возможнаяэнергия – энергия нулевых колебаний
Частица никогда не может
находиться на дне потенциальной
ямы
Расстояние между соседними
уровнями одинаковое









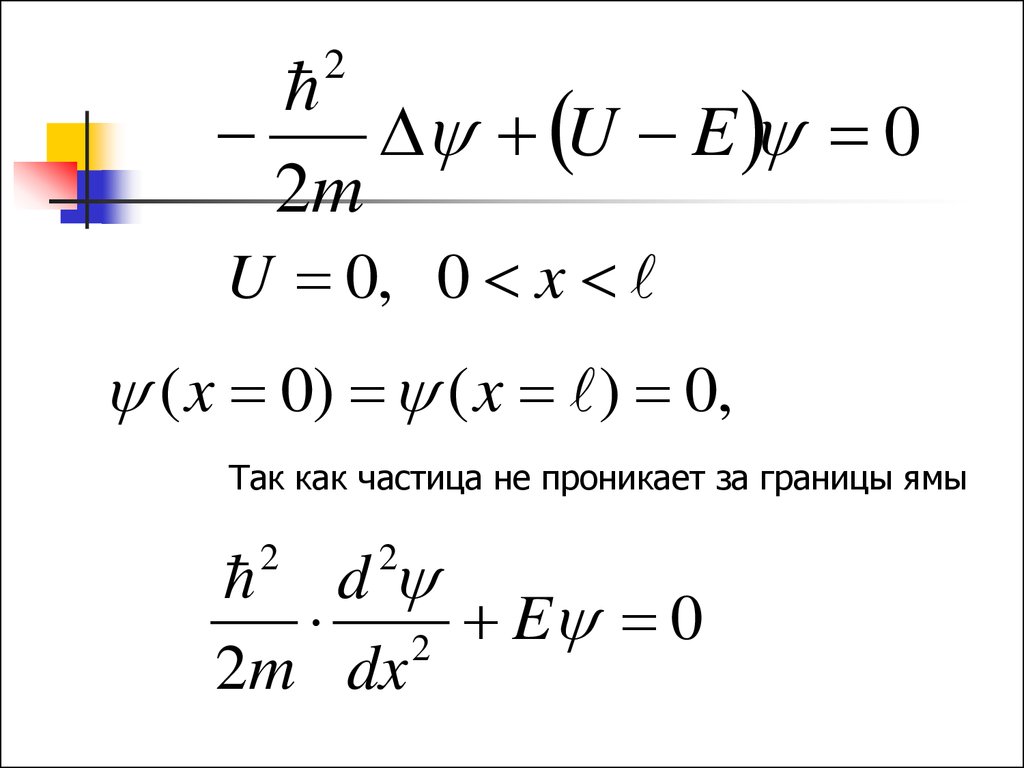
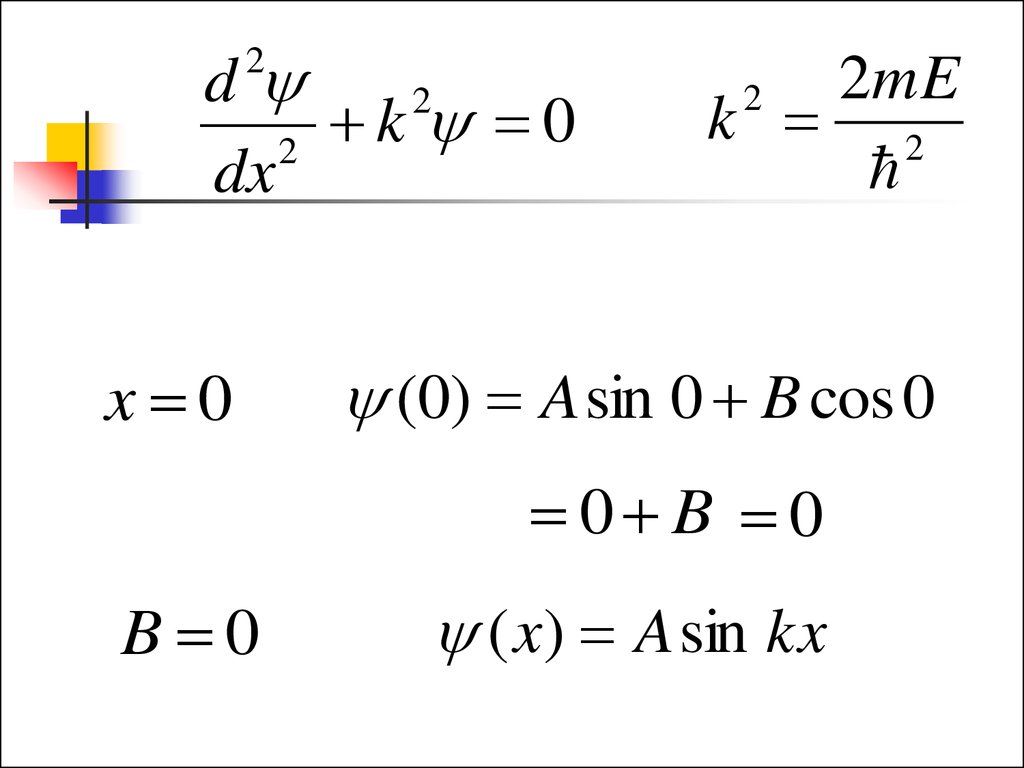












 Физика
Физика








