Похожие презентации:
Движение свободных частиц. Туннельный эффект
1. Движение свободных частиц. Туннельный эффект.
Тема 4.2 «КВАНТОВОМЕХАНИЧЕСКАЯ МОДЕЛЬАТОМА»
Движение свободных частиц.
Туннельный эффект.
2. Движение свободных частиц. Туннельный эффект.
1.2.
3.
4.
Движение свободной частицы.
Частица в одномерной потенциальной яме с абсолютно
непроницаемыми стенками. Квантование энергии.
Гармонический осциллятор в квантовой механике.
Принцип соответствия.
Прохождение частицы через одномерный
потенциальный барьер. Туннельный эффект.
Коэффициент прозрачности.
3. 1. Движение свободной частицы.
Свободная частица — частица, движущаяся в отсутствие внешнихполей.
Так как на свободную частицу, движущуюся вдоль оси х,
силы не действуют, то потенциальная энергия частицы U(x)=const
и ее можно принять равной нулю. Тогда полная энергия частицы
совпадает с ее кинетической энергией.
Тогда уравнение Шредингера для стационарных состояний:
примет вид:
2m
2 E U 0
2 2m
2 E 0
2
x
2
2
k
0
2
x
2
2
m
p
k 2 2 E X2
4.
Энергия свободной частицыпринимать любые значения:
может
2 k 2 p 2X
E
2m 2m
Т.е.:
Энергетический спектр свободной частицы
непрерывен.
Плотность вероятности не зависит ни от
времени, ни от координат:
Все положения свободной
пространстве равновероятны.
частицы
в
A
2
2
2
5. 2. Частица в одномерной потенциальной яме с абсолютно непроницаемыми стенками. Квантование энергии.
Потенциальная яма – ограниченнаяобласть пространства с пониженной
потенциальной энергией частицы.
l – ширина ямы, k – волновое число,
Е – полная энергия частицы.
Потенциальная энергия частицы:
U
, x 0
U x 0, 0 x l
, x l
U
U=0
l
Стационарное уравнение Шредингера в пределах ямы (0 < х < l):
2 2m
2 E 0
2
x
2
2
k
0
2
x
6.
Граничные условия:Общее решение
уравнения Шредингера:
0 l 0
x A sin kx B cos kx
B 0
x A sin kx
Условию
удовлетворяет:
l A sin kl 0
k n
l
n 1,2,3,...
7.
Из условия нормировки:n x
A sin
dx 1
l
0
2
l
2
2
A
l
Собственные функции:
Нормированные
собственные функции:
n x
n x A sin
l
2
n x
n x
sin
l
l
n 1,2,3,...
8.
Т.к.:Собственные значения энергии
частицы:
2mE
n
k 2 ; k
l
2
2 2 2
En
n
2
2ml
n 1,2,3,...
Спектр энергий частицы в
потенциальной яме дискретен.
Значения энергии «квантуются».
Еn – уровни энергии,
n – квантовое число.
E1
2
2ml
2 2
Минимальная энергия (основное
состояние) при n=1:
9.
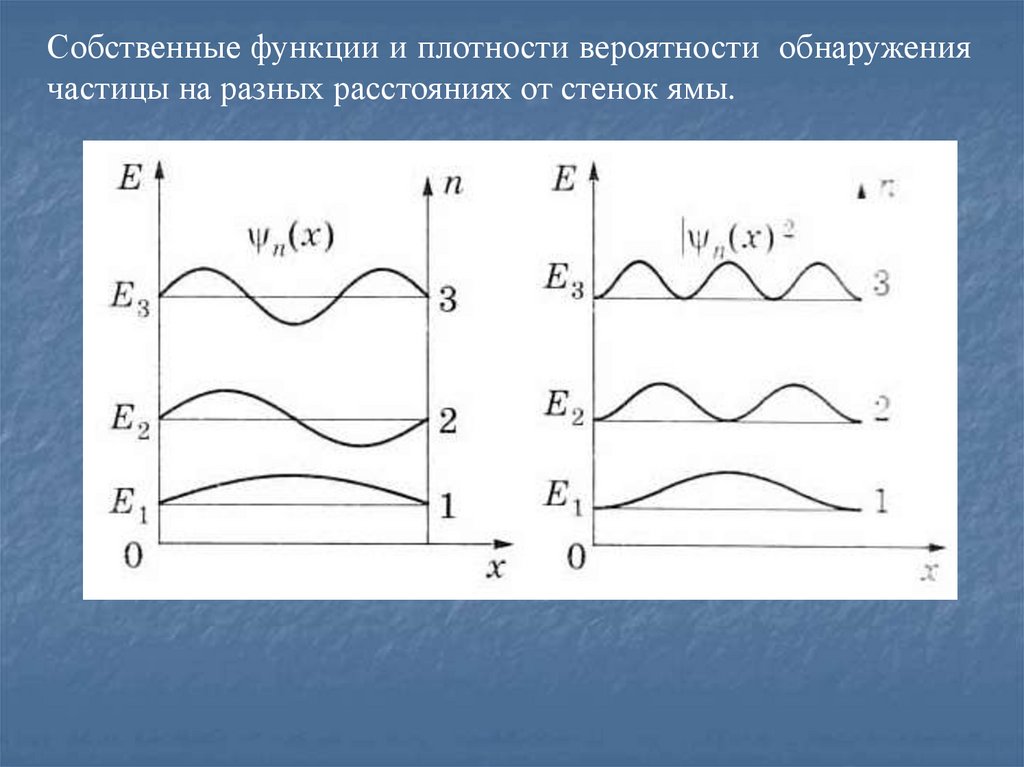
Собственные функции и плотности вероятности обнаружениячастицы на разных расстояниях от стенок ямы.
10. 3. Гармонический осциллятор в квантовой механике.
Линейный (одномерный) гармонический осциллятор – система,совершающая одномерное движение под действием квазиупругой
силы.
Потенциальная энергия линейного гармонического осциллятора:
2 2
m o x
2
U
Уравнения Шредингера для линейного гармонического осциллятора
в квантовой механике:
d 2 2m
m o2 x 2
0
2 E
2
z
dx
11.
Собственные значения энергиигармонического осциллятора:
1
E n n o
2
n 1,2,3,...
Энергия нулевых колебаний
гармонического осциллятора:
o
Eo
2
Энергия нулевых колебаний
гармонического осциллятора следствие
соотношения
неопределенностей: частица не
может находиться на дне
потенциальной
ямы
независимо от ее формы.
12.
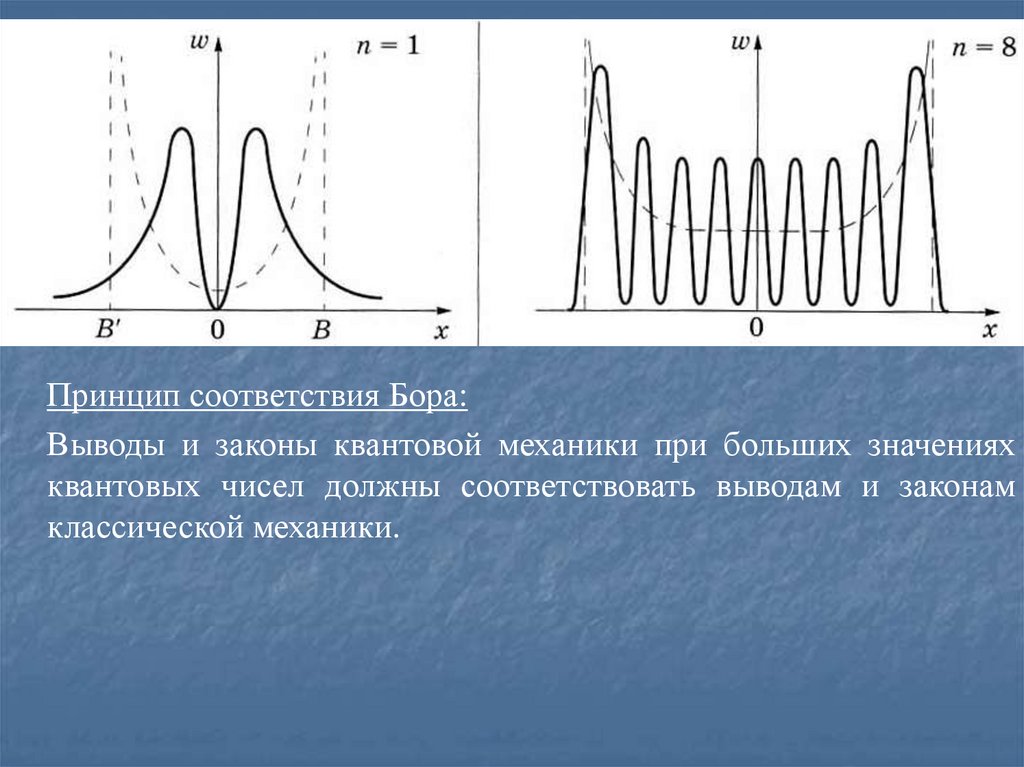
Принцип соответствия Бора:Выводы и законы квантовой механики при больших значениях
квантовых чисел должны соответствовать выводам и законам
классической механики.
13. 4. Прохождение частицы через одномерный потенциальный барьер. Туннельный эффект. Коэффициент прозрачности.
Потенциальная энергия частицы:0, x 0
U x U 0 , 0 x l
0, x l
Для E>U0 уравнение Шредингера
для области 1 и 3:
для области 2:
14.
Общие решения уравнений Шредингера:При E>U0 волна на границе 1 и 2 частично отражается и
частично проходит в область 2, затем она опять на границе 2 и
3 частично отражается и частично проходит в область 3. В
области 2 длина волны де Бройля больше, чем в областях 1 и 3
15.
Для E<U0:уравнение Шредингера для
области 1 и 3:
для области 2:
16.
Общие решения уравнений Шредингера:При E<U0 согласно квантовой механике, микрочастица может
«пройти» сквозь потенциальный барьер. Это специфическое
квантовое явление получило название туннельного эффекта.
17.
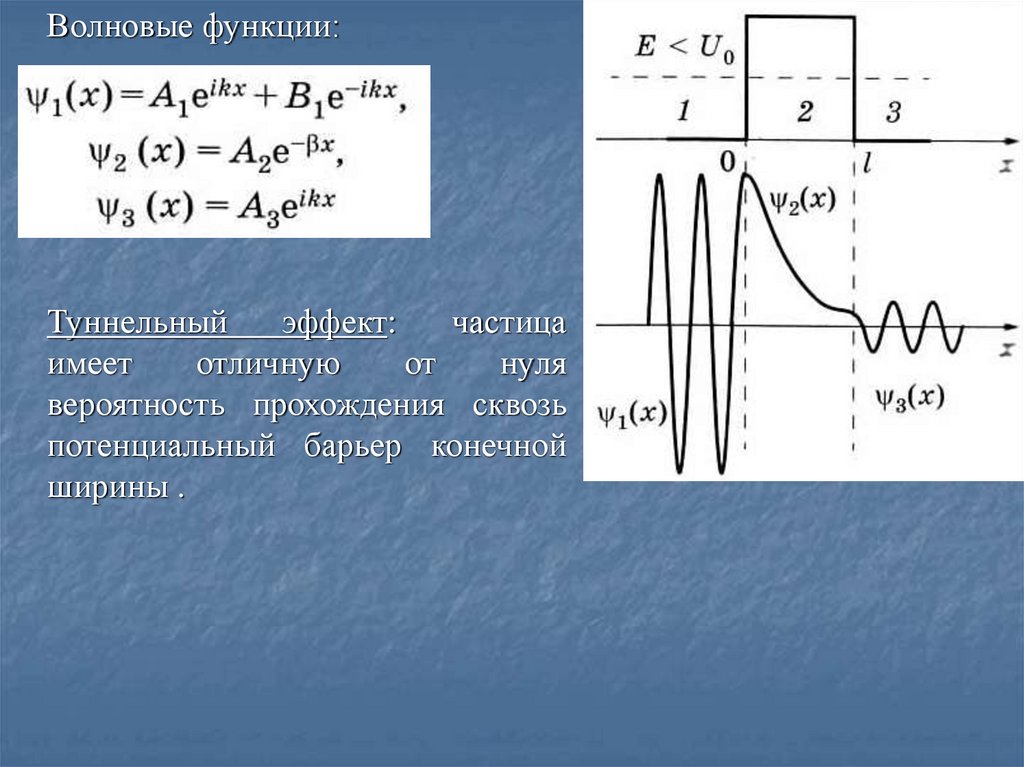
Волновые функции:Туннельный
эффект:
частица
имеет
отличную
от
нуля
вероятность прохождения сквозь
потенциальный барьер конечной
ширины .
18.
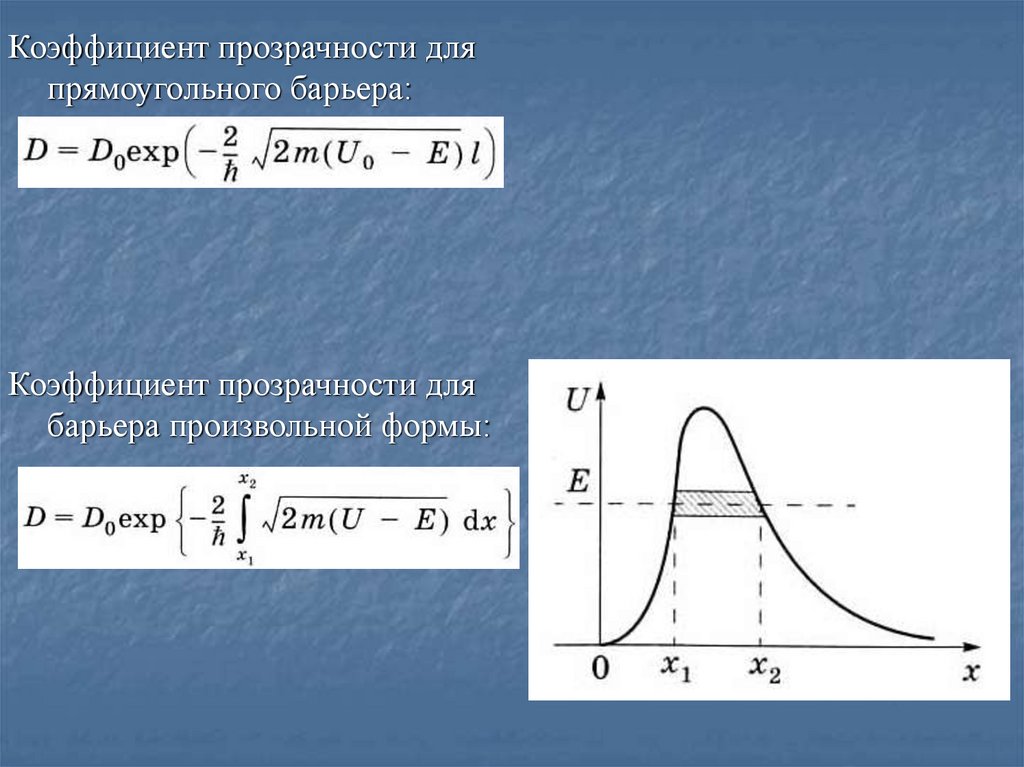
Коэффициент прозрачности дляпрямоугольного барьера:
Коэффициент прозрачности для
барьера произвольной формы:
19.
Выводы:При Е < U0 по классической теории частицы не смогут
преодолеть потенциального барьера и отразятся от него;
согласно квантовой теории, часть частиц отражается, а часть
имеет отличную от нуля вероятность пройти сквозь
потенциальный барьер.
При Е > U0, по классической теории все частицы преодолевают
потенциальный барьер; согласно квантовой теории, часть
частиц проходит, а часть отражается. Как подбарьерное
прохождение, так и надбарьерное отражение являются
специфическими квантовыми эффектами, связанными с
волновыми свойствами частиц.















 Физика
Физика








